Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач
Содержание
- 1. Решение задач
- 2. Порядок решения задач1. Разобраться в условии задачи,
- 3. Порядок решения задач6. Преобразовать (решить) составленные уравнения
- 4. Анализ графиковПример 4. Небольшое тело движется в
- 5. Анализ графиковПример 5:Два точечных тела 1 и
- 6. Анализ грфиковРешение 5:Скорость тела равна углу наклона
- 7. Анализ графиковПример 6:Точечное тело Т начинает двигаться
- 8. Анализ графиков 75Пример 7:Автомобиль движется вдоль прямой
- 9. Анализ графиков 1Пример 8:Точечное тело равномерно движется
- 10. Анализ графиков 0Пример 10:Точечное тело начинает прямолинейное
- 11. Решение задач КинематикаАнализ графиковРавномерное движение, относительность движенияРавнопеременное движение, ускорение телаДвижение по окружности
- 12. Пример 1.2.1:На рисунке представлен график зависимости пути
- 13. Равномерное движение, относительность движенияПример 1.2.2 На рисунке
- 14. Равномерное движение, относительность движения 0,7Пример 1.2.3. Пловец
- 15. Равномерное движение, относительность движенияПример 1.2.4. Велосипедист, двигаясь
- 16. Равномерное движение, относительность движения 20Пример 1.2.5. Движение
- 17. Равномерное движение, относительность движения18Пример 1.2.6. Пешеход идет
- 18. 1.2.7. Катер плывёт по прямой реке, двигаясь
- 19. Решение 1.2.7Вектор скорости катера относительно воды разложим
- 20. Скачать презентанцию
Порядок решения задач1. Разобраться в условии задачи, записать исходные данные, перевести в систему СИ2. Сделать схематический рисунок и/или график(и)3. Выяснить, какие теоретические положения связаны с рассматриваемой задачей в целом и с
Слайды и текст этой презентации
Слайд 1Решение задач
Кинематика
Анализ графиков
Равномерное движение, относительность движения
Равнопеременное движение, ускорение тела
Движение по
окружности
Слайд 2Порядок решения задач
1. Разобраться в условии задачи, записать исходные данные,
перевести в систему СИ
2. Сделать схематический рисунок и/или график(и)
3. Выяснить,
какие теоретические положения связаны с рассматриваемой задачей в целом и с ее отдельными элементами4. Отобрать те формулы, с помощью которых можно описать физическую ситуацию задачи
5. Записать уравнение (систему уравнений), выражающее условие задачи
Слайд 3Порядок решения задач
6. Преобразовать (решить) составленные уравнения относительно искомой величины
8.
Решить уравнение в численном виде
7. Проверить полученное решение с помощью
анализа размерностей9. Оценить правдоподобность ответа, продумать, разумным ли получилось численное значение искомой величины
Слайд 4Анализ графиков
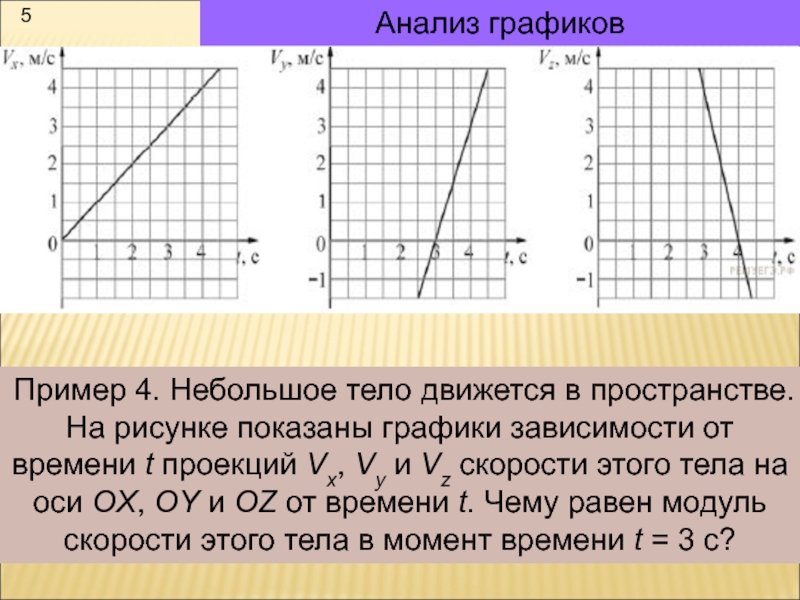
Пример 4. Небольшое тело движется в пространстве. На рисунке
показаны графики зависимости от времени t проекций Vx, Vy и
Vz скорости этого тела на оси OX, OY и OZ от времени t. Чему равен модуль скорости этого тела в момент времени t = 3 с?
5
Слайд 5Анализ графиков
Пример 5:
Два точечных тела 1 и 2 движутся вдоль
оси OX. Зависимости координат x этих тел от времени t
изображены на рисунке. В какой момент времени проекции скоростей этих тел будут приблизительно одинаковыми? Ответ укажите с точностью до целого.
Слайд 6Анализ грфиков
Решение 5:
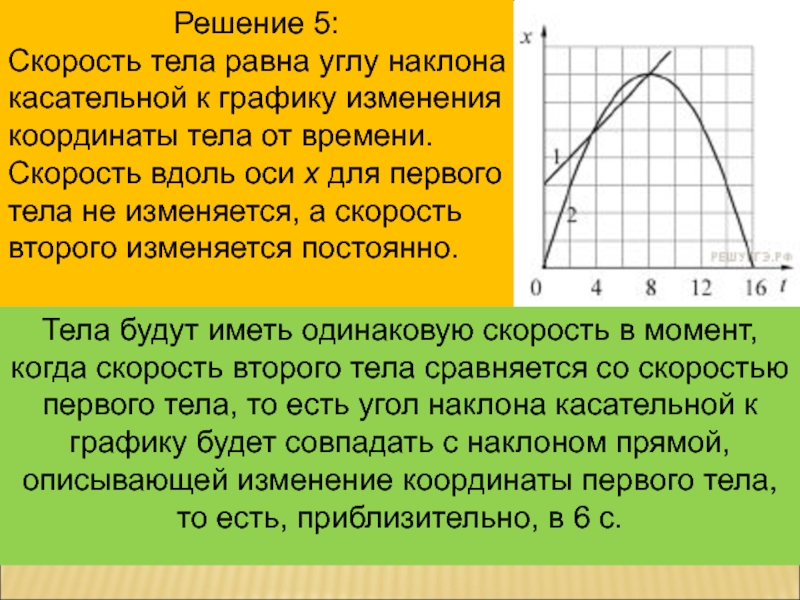
Скорость тела равна углу наклона касательной к графику
изменения координаты тела от времени.
Скорость вдоль оси x для первого
тела не изменяется, а скорость второго изменяется постоянно.
Тела будут иметь одинаковую скорость в момент, когда скорость второго тела сравняется со скоростью первого тела, то есть угол наклона касательной к графику будет совпадать с наклоном прямой, описывающей изменение координаты первого тела, то есть, приблизительно, в 6 с.
Слайд 7Анализ графиков
Пример 6:
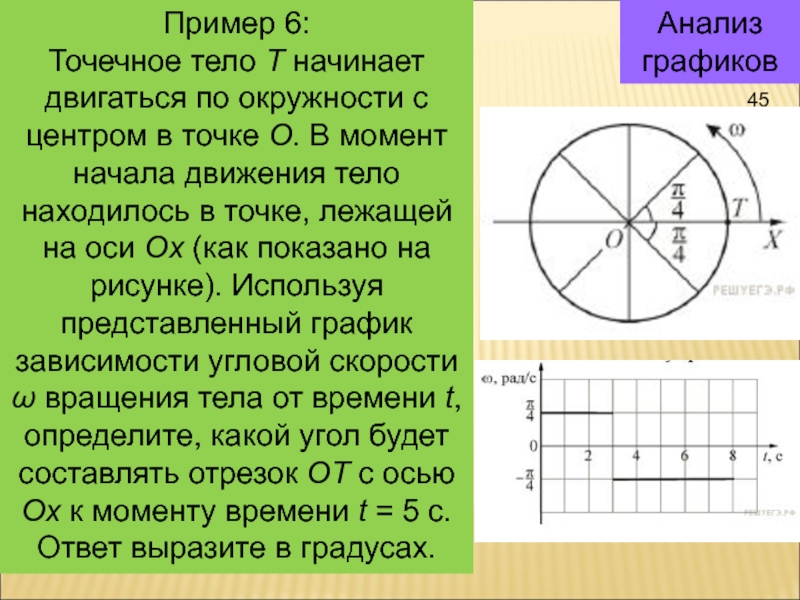
Точечное тело Т начинает двигаться по окружности с
центром в точке О. В момент начала движения тело находилось
в точке, лежащей на оси Ox (как показано на рисунке). Используя представленный график зависимости угловой скорости ω вращения тела от времени t, определите, какой угол будет составлять отрезок OT с осью Ox к моменту времени t = 5 с. Ответ выразите в градусах.
45
Слайд 8Анализ графиков 75
Пример 7:
Автомобиль движется вдоль прямой дороги. На рисунке
представлен график зависимости проекции a его ускорения от времени t.
Известно, что при t = 0 автомобиль покоился. Какой путь прошёл автомобиль за промежуток времени от 10 с до 15 с? Ответ выразите в метрах.
Слайд 9Анализ графиков 1
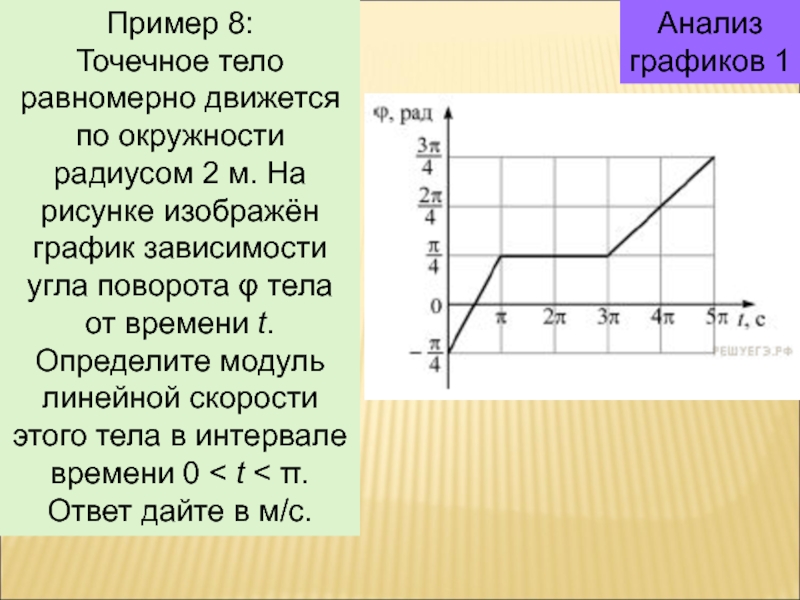
Пример 8:
Точечное тело равномерно движется по окружности радиусом
2 м. На рисунке изображён график зависимости угла поворота φ
тела от времени t. Определите модуль линейной скорости этого тела в интервале времени 0 < t < π. Ответ дайте в м/с.
Слайд 10Анализ графиков 0
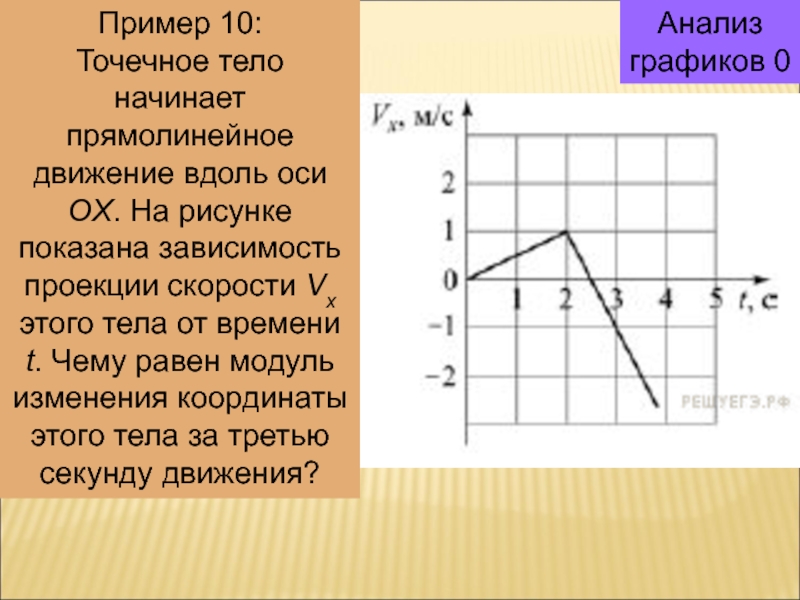
Пример 10:
Точечное тело начинает прямолинейное движение вдоль оси
OX. На рисунке показана зависимость проекции скорости Vx этого тела
от времени t. Чему равен модуль изменения координаты этого тела за третью секунду движения?
Слайд 11Решение задач
Кинематика
Анализ графиков
Равномерное движение, относительность движения
Равнопеременное движение, ускорение тела
Движение по
окружности
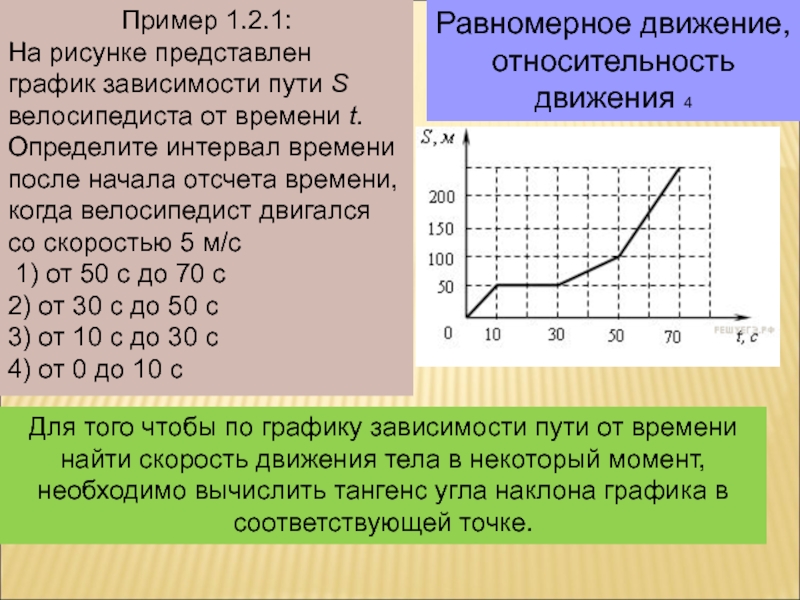
Слайд 12Пример 1.2.1:
На рисунке представлен график зависимости пути S велосипедиста от
времени t. Определите интервал времени после начала отсчета времени, когда
велосипедист двигался со скоростью 5 м/с1) от 50 с до 70 с
2) от 30 с до 50 с
3) от 10 с до 30 с
4) от 0 до 10 с
Равномерное движение, относительность движения 4
Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке.
Слайд 13Равномерное движение, относительность движения
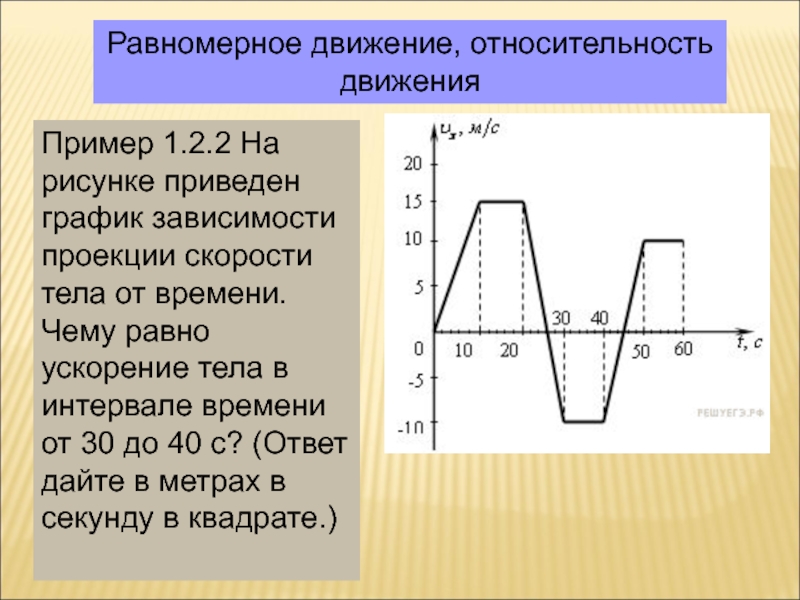
Пример 1.2.2 На рисунке приведен график зависимости
проекции скорости тела от времени. Чему равно ускорение тела в
интервале времени от 30 до 40 с? (Ответ дайте в метрах в секунду в квадрате.)
Слайд 14Равномерное движение, относительность движения 0,7
Пример 1.2.3. Пловец плывет по течению
реки. Определите скорость пловца относительно берега, если скорость пловца относительно
воды 0,4 м/с, а скорость течения реки 0,3 м/с.0,3 м/с
4 м/с
Слайд 15Равномерное движение, относительность движения
Пример 1.2.4. Велосипедист, двигаясь под уклон, проехал
расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно
он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Слайд 16Равномерное движение, относительность движения 20
Пример 1.2.5. Движение двух велосипедистов заданы
уравнениями Х1=2t и X2=100-8t
Найдите координату X места встречи велосипедистов. Велосипедисты
двигаются вдоль одной прямой. (Ответ дайте в метрах.) 
Слайд 17Равномерное движение, относительность движения18
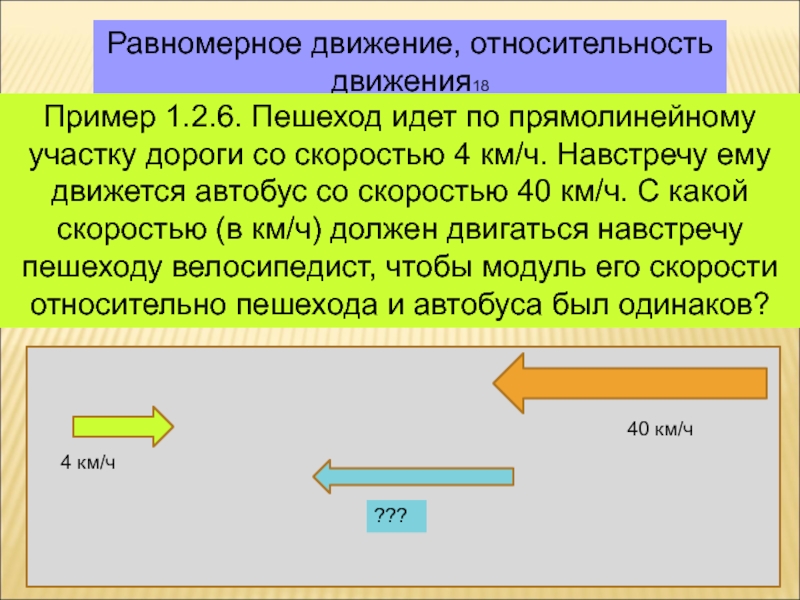
Пример 1.2.6. Пешеход идет по прямолинейному участку
дороги со скоростью 4 км/ч. Навстречу ему движется автобус со
скоростью 40 км/ч. С какой скоростью (в км/ч) должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?4 км/ч
40 км/ч
???
Слайд 181.2.7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно
береговой линии. Модуль скорости катера относительно берега равен 6 км/ч.
Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч. (21)
Слайд 19Решение 1.2.7
Вектор скорости катера относительно воды разложим на два компонента:
1- вектор направлен параллельно берегу, 2- вектор — перпендикулярно берегу.
Для того чтобы катер в системе отсчёта, связанной с берегом, двигалась перпендикулярно к нему, необходимо, чтобы компонент скорости катера относительно воды вдоль реки в точности компенсировала скорость течения.Тогда модуль скорости катера относительно воды будет равен (по теореме Пифагора)
