Слайд 1Выступление на РМО учителей математики
по теме:
Решение задач ОГЭ
«Модуль
геометрия»
часть 2
Копанева Нэля Николаевна -
учитель математики
1 квалификационной категории
МОБУ «Кузнецовская
средняя общеобразовательная школа»
с.Кузнецово, 2016 г.
Слайд 2Вступление
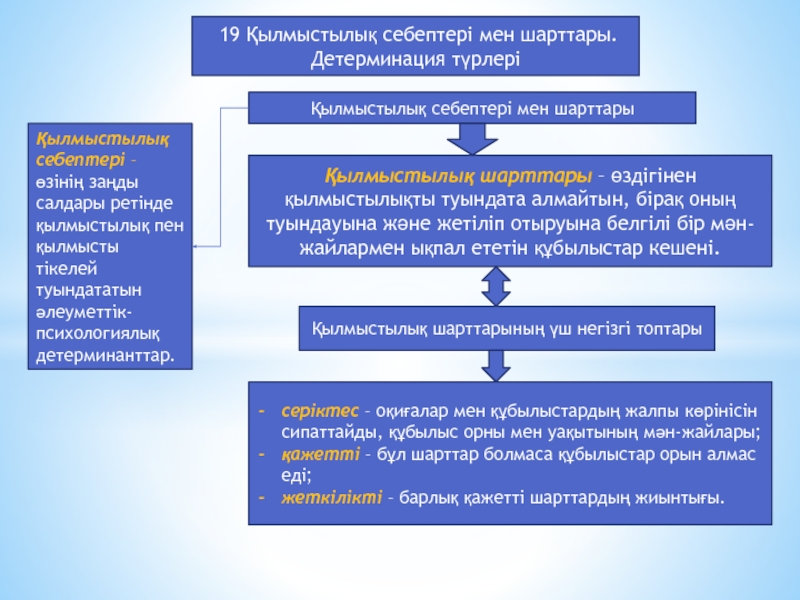
Проблема – как подготовить выпускников к успешной сдаче экзамена встаёт
перед каждым учителем.
Основная подготовка выпускников к ОГЭ по математике осуществляется
не только в течение всего учебного года в старшей школе, но и раньше, начиная с 7 класса. Исключительно важным становится целенаправленная и специально планируемая подготовка школьников к ОГЭ. Безусловно, на последние годы обучения в школе приходится максимальная нагрузка на учащихся. При этом возрастает роль и ответственность в подготовительной работе и учителя, и самого ученика. Моя цель, как учителя, помочь ребёнку в подготовке к ГИА, разобраться в самых значимых моментах в подготовительной работе, знать существующую документацию по проведению экзамена.
Слайд 3Задачи по подготовке учащихся к ОГЭ:
1. Начинать подготовку к итоговой
аттестации с 5 класса;
2. Создавать учебный материал (по
типу ГИА) и использовать готовые печатные и электронные пособия;
3. Учить школьников ≪технике сдачи теста≫;
4. Психологический настрой к ГИА;
5. Через систему дополнительных занятий ( факультативов, курсов, индивидуальных консультаций) повышать интерес к предмету и личную ответственность школьника за результаты обучения.
Слайд 4
Как я строю свою работу по подготовке учащихся
к сдаче экзамена по математике в форме ГИА?
1) провожу
исследование демо-версий ГИА по математике последних лет, взятые на сайте www. fipi. ru, http://rcoi12.ru/gia9/ - организация ГБУ Республики Марий Эл "ЦИТОКО" . Анализирую результаты прошлых лет, делаю выводы.
2) соотношу своё календарно-тематическое планирование в данных классах с темами, используемыми в КИМах. Затем произвожу отбор тех заданий, работу над которыми уже можно начинать в 7-8 классах.
3) осуществляю подбор необходимой литературы: дидактические материалы, тесты и др.
4) В зависимости от класса, учащихся можно разбить на группы. Чтобы строить работу дифференцированно, не забывая об учащихся с повышенной мотивацией и слабоуспевающих, проводя индивидуальные консультации. Рекомендую использование Интернет-ресурсов для самостоятельной домашней подготовки к экзамену. Слабоуспевающим ученикам не всегда удаётся справиться с предлагаемыми заданиями в классной и домашней работе. С ними отрабатываем те задания, которые вызывают затруднения. Решаю с ними примеры и задачи подобного характера. Эти меры необходимы, для преодоления ими «нижнего порога» на ГИА.

Слайд 5 Предлагаю решение задач ОГЭ
«Модуль геометрия» часть 2 вариант 261 диагностического
тестирования.
Слайд 6
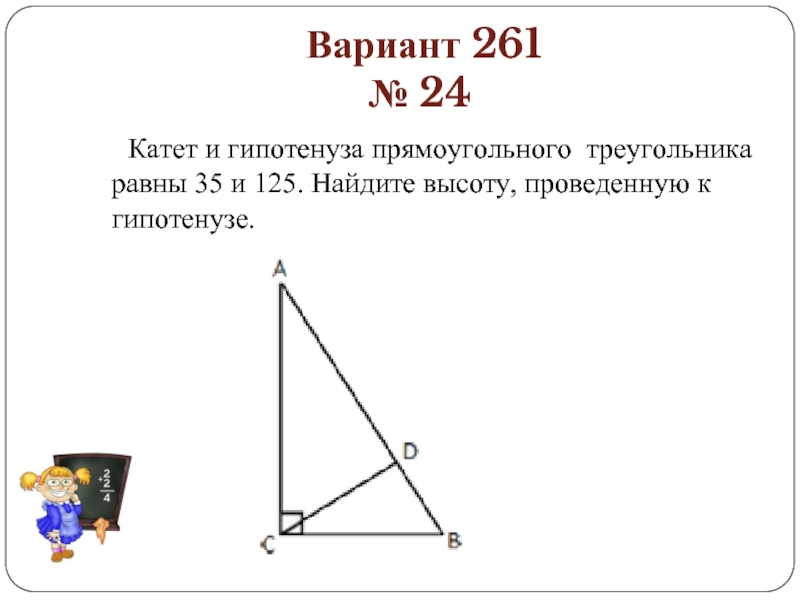
Вариант 261
№ 24
Катет и гипотенуза прямоугольного треугольника равны
35 и 125. Найдите высоту, проведенную к гипотенузе.
Слайд 7№ 24
1 сп.
1) AB - гипотенуза, BC - катет.
Найдем AC по теореме
Пифагора:
AB2=BC2+CA2
1252=352+CA2
15625=1225+CA2
14400=CA2
CA=120
2) Вычислим площадь треугольника АВС
S = ½ * СВ* АС
S
= ½ * 35 * 120 = 2100
3) Воспользуемся формулой площади треугольника
S = ½ * АВ *СД
2100 = ½ * 125 * СД
СД = 4200 : 125 = 33,6
Ответ: СД= 33,6
2 сп.
1) AB - гипотенуза, BC - катет.
Найдем AC по теореме Пифагора:
AB2=BC2+CA2
1252=352+CA2
15625=1225+CA2
14400=CA2
CA=120
2) Для Δ ABC
sin A= СВ/АВ = 35/125 = 7/25
3) Для Δ ACD
sin A= СД/СА
CД=AC*sin A=120* 7/25 = 33,6
Ответ: СД= 33,6
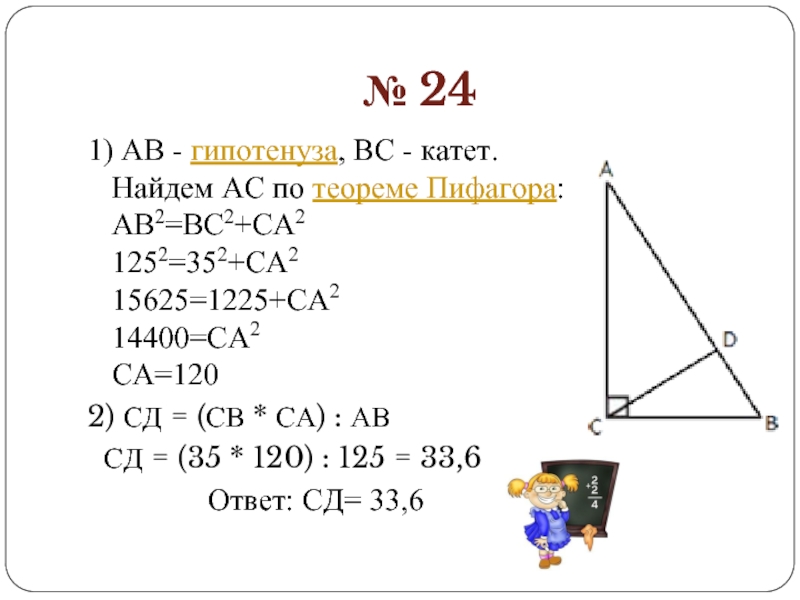
Слайд 8№ 24
1) AB - гипотенуза, BC - катет.
Найдем AC по теореме Пифагора:
AB2=BC2+CA2
1252=352+CA2
15625=1225+CA2
14400=CA2
CA=120
2)
СД = (СВ * СА) : АВ
СД = (35
* 120) : 125 = 33,6
Ответ: СД= 33,6
Слайд 9 Длина высоты, проведенной к гипотенузе, равна отношению произведения катетов
к гипотенузе. Если обозначить длины катетов через a и b,
длину гипотенузы — через с, формулу можно переписать в виде
Слайд 10№ 25
Основания BC и AD трапеции ABCD равны соответственно 5
и 45, BD=15. Докажите, что треугольники CBD и ADB подобны.
ABCD - трапеция, следовательно, AD||BC.
∠CBD=∠ADB (т.к. это накрест-лежащие углы
для параллельных прямых AD и BC
и секущей ВД).
Рассмотрим отношения сторон:
BC/BD= 5/45=1/3
BD/AD=15/45=1/3
Тогда по второму признаку подобия треугольников, треугольники CBD и ADB подобны.
Слайд 11№ 26
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC.
Окружность проходит через точки C и D и касается прямой
AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=8, BC=7.
Слайд 12№ 26
1 сп.
По условию
задачи AB перпендикулярна BC, следовательно перпендикулярна и AD (т.к. в трапеции основания
параллельны).
Расстояние от точки Е до прямой CD - отрезок, перпендикулярный CD и проходящий через точку Е.
1) Рассмотрим треугольники TCB и CKD.
∠CTB=∠DCK (т.к. это соответственные углы при параллельных прямых TA и CK) ∠TBC=∠CKD=90°
Следовательно, эти треугольники подобны (по первому признаку подобия).
Тогда, BC/KD=TC/CD 7/1=TC/CD TC=7 *CD
По теореме о касательно и секущей:
TE2=TD*TC=(TC+CD)*TC=(7*CD+CD)*7*CD=8*CD*7*CD=
= 56*CD2
TE=CD*√56=2*CD*√14
Рассмотрим треугольники TEF и TAD. ∠CTB - общий
∠EFT=∠TAD=90°
Следовательно, применив теорему о сумме углов треугольника, получаем, что ∠TEF=∠ADT.
Следовательно, cos∠TEF=cos∠ADT.
EF=TE*cos∠TEF=TE*cos∠ADT=TE/CD=2*CD*√14/CD=2√14
Ответ: EF=2√14
Слайд 13№ 26
2 сп.
Рассмотрим многоугольник ЕВСК и DАЕК, они подобны, т.к.
ВС/ЕК = ЕК/АД.
Отсюда имеем: 7/ЕК = ЕК/8,
ЕК²= 56, ЕК= 2√14.
Ответ: ЕК= 2√14.
Слайд 14
Теорема о касательной и секущей
Если из точки, лежащей
вне окружности, проведены касательная и секущая, то квадрат длины касательной
равен произведению секущей на ее внешнюю часть: MC2 = MA*MB.
Слайд 15Подобные многоугольники
Два одноимённых многоугольника называются подобными, если углы одного из
них соответственно равны углам другого, а сходственные стороны многоугольников пропорциональны.
Одноимёнными
называются многоугольники, имеющие одинаковое число сторон (углов).
Сходственными называются стороны подобных
многоугольников, соединяющие вершины соответственно
равных углов
.
<А = <А’, <В = <В’, <С = <С’,
Слайд 16 В этом году готовлю учащихся 9 класса к сдаче ОГЭ.
В
течение учебного года провожу инструктажи по заполнению бланков, ознакомлению учащихся
с демовариантом ОГЭ, правилами поведения на экзамене.
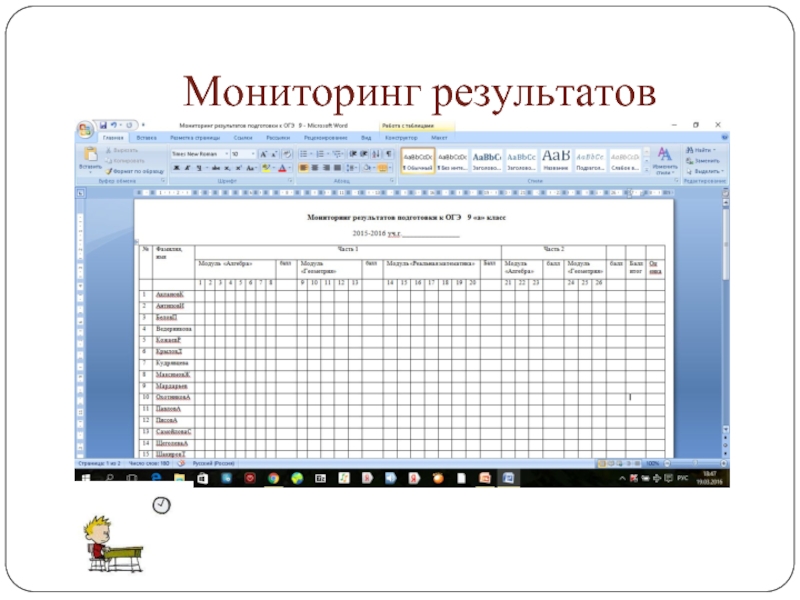
Слайд 17 Для того чтобы наглядно видеть уровень подготовленности выпускников к сдаче
ГИА результаты выполнения диагностических и тренировочных работ отражаются в таблице.
Слайд 20
Полезные ссылки для подготовки к
ОГЭ-2016
http://www.fipi.ru/ -«Федеральный институт
педагогических измерений»
http://rcoi12.ru/gia9/ -
Организация ГБУ Республики Марий Эл "ЦИТОКО"
http://infourok.ru/- инфоурок
http://www.metod-kopilka.ru/- метод-копилка
mathgia.ru – открытый банк заданий ГИА по математике
sdamgia.ru –образовательный портал для подготовки к ГИА по многим предметам
http://alleng.ru/ Всем, кто учится. Очень много образовательной литературы
http://aksioma72.blogspot.ru/ -блог учителя математики Продан С.В.
Слайд 22http://rcoi12.ru/gia9/ -
Организация ГБУ Республики Марий Эл "ЦИТОКО"
Слайд 23http://mathgia.ru/or/gia12/ -
открытый банк заданий по математике
Слайд 24
http://www.uchportal.ru/video/vic/ogeh_gia_po_matematike/zadacha_24- учительский портал
Слайд 29
http://egeigia.ru/all-gia/materialy-gia/matematika-
ЕГЭ /ОГЭ от урока до экзамена
Слайд 30http://otvet-gotov.ru/- ответ готов
Слайд 31Интернет ресурсы
http://nsportal.ru/ - социальная сеть работников образования
http://otvet-gotov.ru/- - ответ готов
(картинки)
http://go.mail.ru/- картинки дети
Слайд 33 Данная работа предназначена для учителей и учащихся при подготовке
к ОГЭ. Рассматриваются три задачи части 2 диагностического ОГЭ с
различными способами решения, с целью выбора более подходящего вам решения.