решения Неравенств с одной переменной Седьмое апреля Классная работа

нестрогие неравенства»;
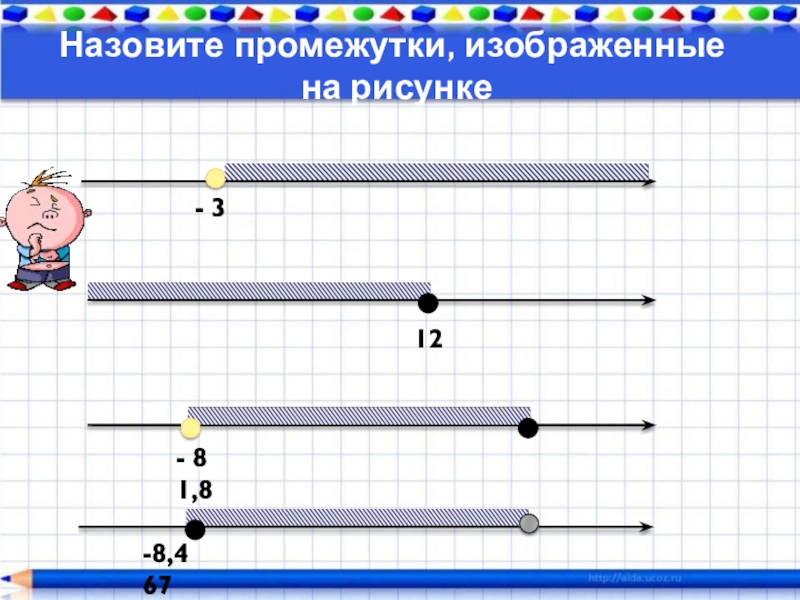
повторить свойства равносильности неравенств, числовые промежутки;
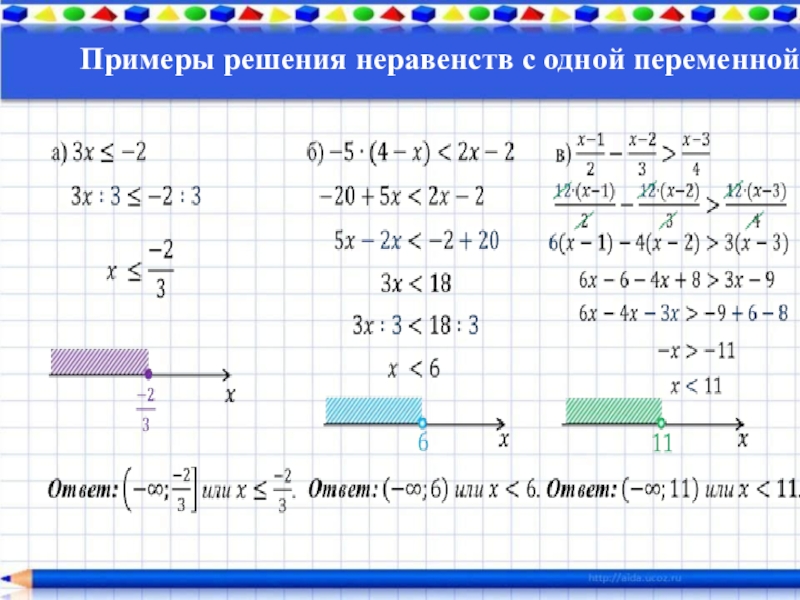
отработать алгоритм решения линейных

неравенств вида
ах > b, ax < b;
закрепить навыки решения линейных неравенств с одной переменной, опираясь на свойства равносильности с изображением множества решений неравенства на координатной прямой.

Неравенства вида ах > b или

ах < b,
где а и b – некоторые числа,
называют линейными неравенствами с одной переменной.
Например: 5х ≤ 15, 3х > 12, - х > 0

Строгие неравенства — это неравенства со знаками больше (>) или меньше (<).

Нестрогие неравенства — это неравенства со знаками больше либо равно(≥) или меньше либо равно(≤).

Повторим основные понятия:

его в верное числовое неравенство.

Решить неравенство – значит найти все

его решения или доказать, что их нет.

Являются ли числа 2 ; 0,2 решением неравенства:
а) 2х – 1 < 4;
б) - 4х + 5 > 3?

одной части неравенства перенести в другую слагаемое с противоположным знаком,

то получится равносильное ему неравенство.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;
если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

не имеющие решений, тоже считают равносильными
2х – 6 > 0

и равносильны х > 3

х2 + 4 ≤ 0 и |х| + 3 < 0 равносильны нет решений

3х – 6 ≥ 0 и 2х > 8 неравносильны
х ≥ 2 х > 4

число 12 решением неравенства 2х>10?

2) Является ли число -6 решением

неравенства 4х>12?

3) Является ли неравенство 5х-15>4х+14 строгим?

4) Существует ли целое число принадлежащее промежутку [-2,8;-2,6]?
5) При любом ли значении переменной а верно неравенство а² + 4 >о?

6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется?

10
- 6,5
- 4
- 3,1

(- ∞; 3)
(2; +

∞)

1,8

-8,4 67

знак равенства.

В 1631 году английский ученый Томас Гарриот ввел знаки

неравенства: <, >.


В 1734 году французский математик Пьер Бугер ввел символы ≤,≥.

Федр (Древнеримский поэт-баснописец)

части делим на отрицательное число
1) – 2х < 4

2) – 2х > 6
3) – 2х ≤ 6

Решите неравенство:

4) – х < 12
5) – х ≤ 0
6) – х ≥ 4

Выполните:
№ 845(а, б)
№ 849(а, г)
№ 854(а, б)

(4-5х)+2(3+х)< 1.

Самостоятельная работа

Теоремы о почленном сложении и умножении числовых неравенств.
Определение пересечения и

объединения числовых множеств.
Определение решения неравенств с одной переменной.
Свойства, используемые при решении
неравенств.
Определение линейных неравенств
с одной переменной.