Санкт-Петербургский государственный политехнический университет Факультет

ДИССЕРТАЦИЯ

на тему:

РАЗРАБОТКА И ПРОГРАММНАЯ РЕАЛИЗАЦИЯ
ПОЛНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

СИНХРОННОГО ГЕНЕРАТОРА
В ФАЗНЫХ КООРДИНАТАХ
И ИССЛЕДОВАНИЕ АВАРИЙНЫХ РЕЖИМОВ ЕГО РАБОТЫ

220100 – Системный анализ и управление


Выполнил студент гр. 6082/1 Рябов Г.А.

Руководитель, к.т.н., с.н.с. Симаков И.П.


Санкт-Петербург
2011

и компьютерная реализация полной математической модели динамики СГ в фазных

(в статорных) координатах для всестороннего исследования переходных процессов в ЭЭС в аварийных режимах (при коротких замыканиях всех возможных видов и обрывах в статорных и роторных обмотках), которые не могут быть рассчитаны с используемой традиционно используемой в теории электрических машин и ЭЭС модели Парка-Горева в «виртуальных» (вращающихся с ротором) координатах.

уравнений электромагнитных и электромеханических процессов в синхронном генераторе в фазных

координатах - в неподвижных (статорных) осях и процессов регулирования частоты и напряжения.

2. Преобразование полученной полной системы уравнений СГ к уравнениям в форме Парка-Горева .

3. Компьютерная реализация в ПК «МВТУ» модели СГ в форме Парка – Горева при работе на АИН
с проведением вычислительных экспериментов по пуску СГ на холостой ход, принятию нагрузки и возникновению «металлических» коротких замыканий.

4. Разработка алгоритмов получения (пересчета) информации для уравнений СГ в фазных
координатах по справочных данным, приводимым, к сожалению, для обеспечения численного
решения уравнений Парка – Горева.

5. Компьютерная реализация в среде ПК «МВТУ» полной математической модели СГ в фазных координатах с элементами анимации и визуализации для однофазных и трехфазных СГ.

6. Исследование динамических процессов при работе СГ на АИН и сравнение полученных результатов с аналогичными результатами, полученными по уравнениям Парка – Горева.

7. Проведение вычислительных экспериментов на полной математической модели СГ в фазных координатах для аварийных режимов, которые невозможно исследовать по уравнениям Парка – Горева, в том числе при всех видах коротких замыканий в статорных цепях СГ, «глухих» или «металлических», одной фазы на «землю», двух фаз на «землю», между фазами и при обрывах в различных цепях СГ и регуляторах напряжения и частоты.

и предположения при математическом описании
насыщение магнитных цепей отсутствует;
отсутствие потерь в

стали;
кривые намагничивающих сил и индукций имеют синусоидальное распределение в пространстве;
индуктивные сопротивления рассеивания не зависят от положения ротора и от тока в обмотках.
Дополнительно для принципиальной отработки компьютерной модели в работе не учитывались (временно) демпферные обмотки.

Схема расположения обмоток генератора

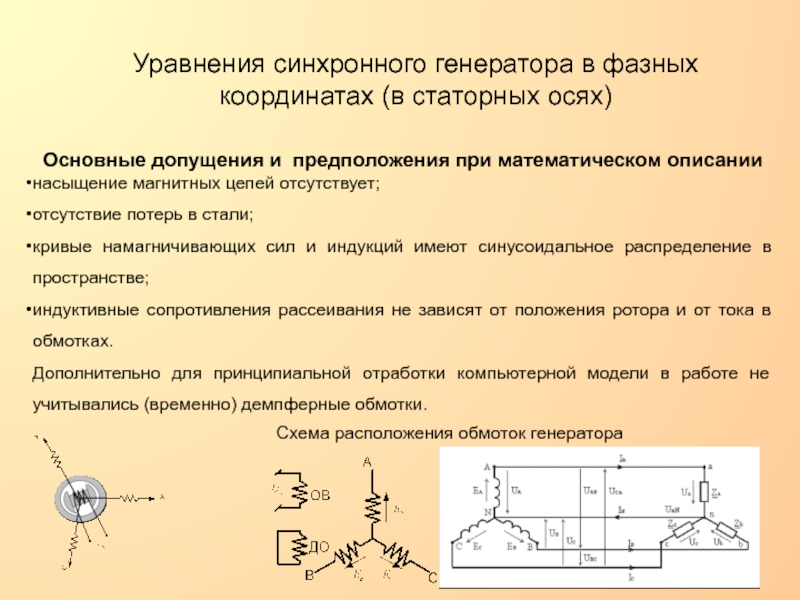
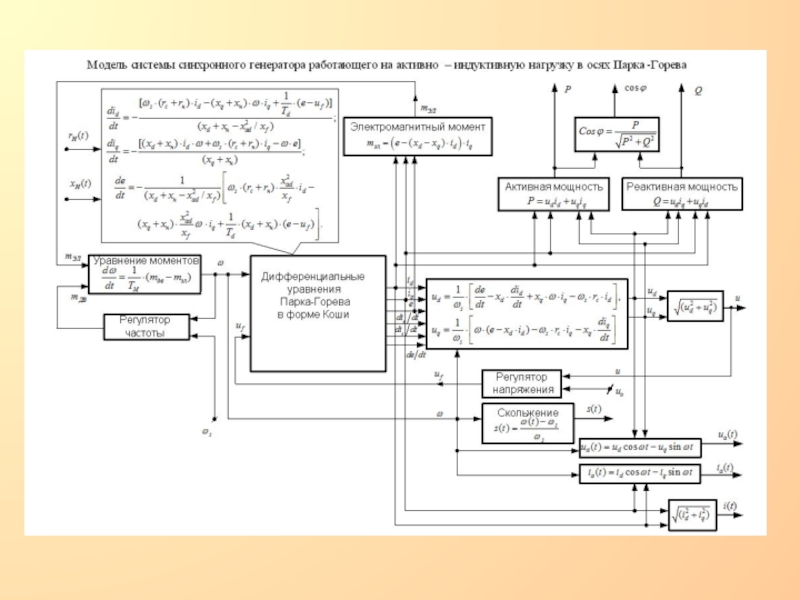
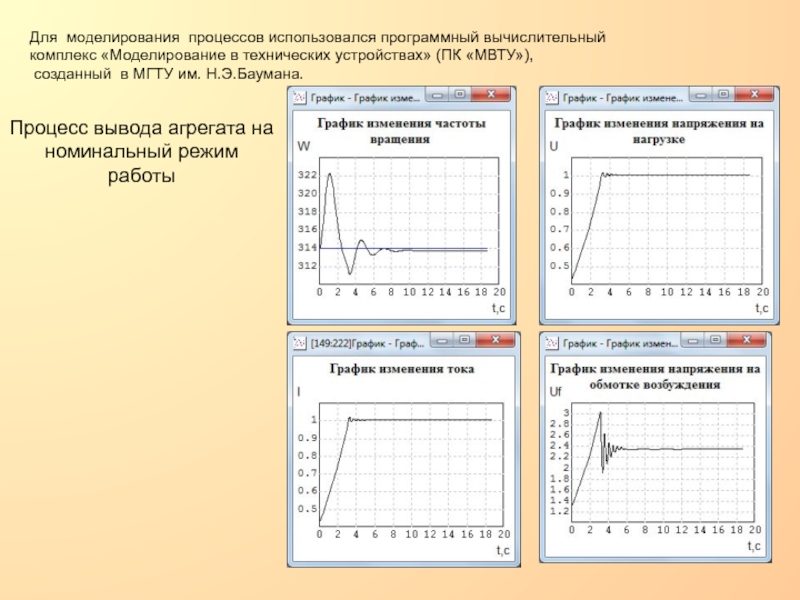
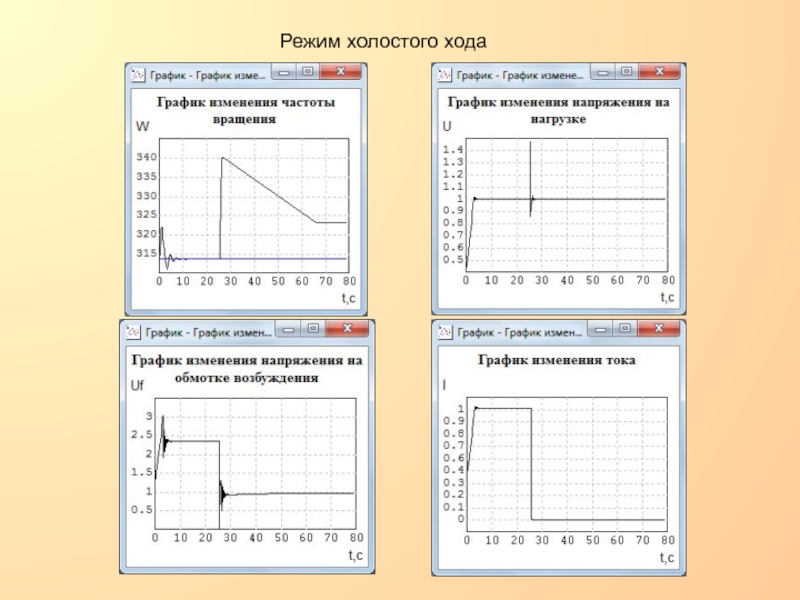
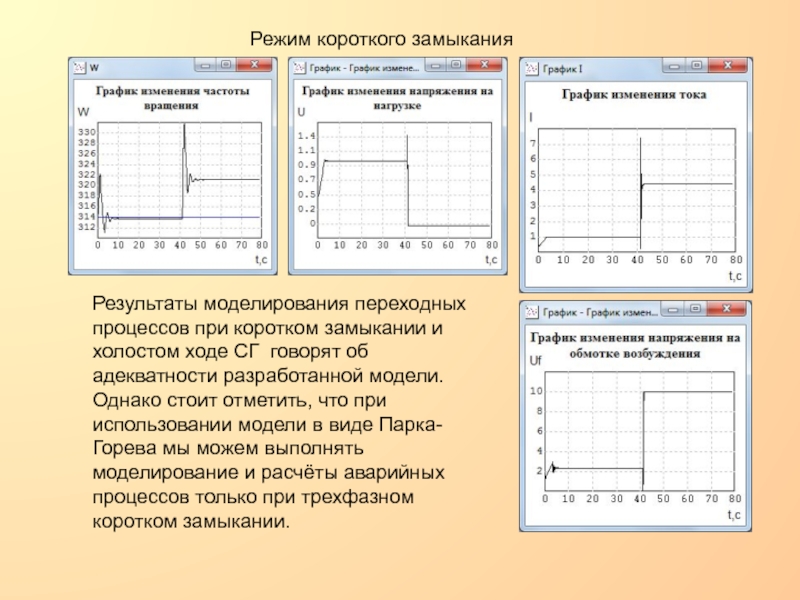
в цепи возбуждения
Связи между потокосцеплениями и токами
Коэффициенты самоиндукции контуров

фаз статора La , Lb , Lc для явнополюсного СГ являются периодическими функциями угла  с периодом 

Коэффициенты взаимной индукции обмоток фаз статора

Mab= Mba= Mcp + Lm Cos(2 -2/3)
Mbc= Mcb= Mcp + Lm Cos 2
Mca= Mac= Mcp + Lm Cos(2 +2/3),

Коэффициенты взаимной индукции обмотки контура возбуждения и обмотками фаз статора

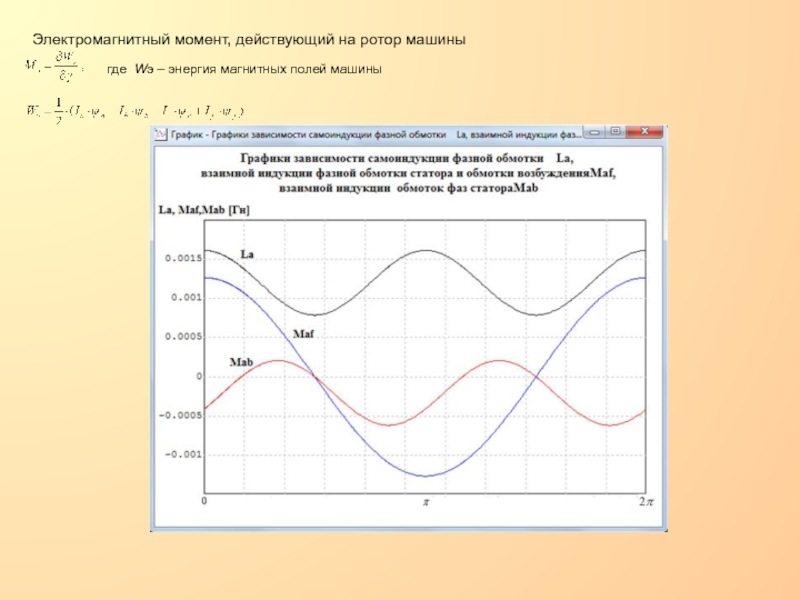
Уравнения моментов:

где J – момент инерции всех вращающихся масс агрегата в целом [кгм2]; Мдв - движущий (механический) момент,приложенный к валу [нм];
Мс - момент сопротивления [нм];

потокосцепления обмоток фаз статора [Вб];

токи в соответствующих обмотках статора и обмотке возбуждения [A];

активные сопротивления обмоток
статора и обмотке возбуждения [];

- напряжения фаз сети

напряжения на зажимах фазных обмоток [B];

коэффициенты самоиндукции фазных обмоток статора

полей машины

линейного преобразования, предложенного Р. Парком (1929 г.), к исходным уравнениям

в фазных координатах приводит к дифференциальным уравнениям с постоянными коэффициентами

Взаимосвязь фазных координат и преобразованных во вращающиеся с ротором координаты:
первая – неподвижная симметричная трёхфазная (a, b, c),
вторая - ортогональная система (d, q, O), вращающаяся с угловой
скоростью ротора   ddt . ось q опережает ось d

уравнений в фазных координатах. Их отличие в следующем:

для идеализированной синхронной

машины они являются уравнениями с постоянными коэффициентами;

все коэффициенты самоиндукции и взаимоиндукции в являются при принятых допущениях постоянными, не зависящими от угла  величинами;

порядок этих уравнений ниже, чем порядок уравнений в фазных величинах;

имеет место меньшее число неизвестных переменных (величин);
неизвестными величинами в них являются проекции обобщённых векторов токов, напряжений и потокосцеплений, то есть фиктивные величины.

Преобразованное уравнение моментов

При этом потокосцепления и электромагнитный момент выражаются следующим образом

относительных единицах и натуральном времени

d = d / б, q

= q / б, ud = Ud / Uб,
uq = Uq / Uб,id = Id / Iб, iq = Iq / Iб,
usd = Usd / Uб, usq = Usq / Uб,  = d / dt, r = R / Zб.

Уравнение цепи возбуждения в относительных единицах и натуральном времени

Td = Lf / R f - постоянная времени цепи возбуждения при разомкнутой цепи статора

s = ( - s ) / s - скольжение ротора генератора
относительно синхронной скорости;

амплитуда номинального статорного напряжения

Уравнения СГ в форме уравнений Парка-Горева в относительных единицах выраженные через токи и напряжения

амплитуда номинального статорного тока

или в эквивалентном виде:
xH , rH - индуктивная

и активная составляющие нагрузки в о.е..

С учетом уравнений нагрузки дифференциальные уравнения Парка-Горева в форме Коши имеют вид:

Напряжение на зажимах генератора находим по формулам:

динамической нелинейности типа «упор»
Модель сервопривода в «арифметизованном» виде
Модель автоматического

регулятора частоты можно представить в виде блок схемы:

устройствах» (ПК «МВТУ»),
созданный в МГТУ им. Н.Э.Баумана.
Процесс вывода

агрегата на
номинальный режим
работы

коротком замыкании и холостом ходе СГ говорят об адекватности разработанной

модели. Однако стоит отметить, что при использовании модели в виде Парка-Горева мы можем выполнять моделирование и расчёты аварийных процессов только при трехфазном коротком замыкании.

пересчета относительных единиц в физические:
Уравнение СГ в матричном виде:

вид:
Уравнение СГ в фазных координатах с учетом АИН :
Электромагнитный момент:
Уравнения

регулятора
частоты

Уравнения регулятора напряжения:

короткое замыкание

результаты.
В диссертации разработана и программно реализована полная компьютерная математическая

модель динамики СГ в фазных координатах с автоматическими регуляторами напряжения и частоты вращения ротора и статической АИН, предназначенная для исследования широкого набора аварийных режимов, которые невозможно исследовать с использованием традиционных моделей Парка - Горева.

Сделан подробный вывод полных уравнений динамики СГ в фазных координатах и способ их приведения к форме Парка – Горева без пренебрежения динамикой электромагнитных процессов в статорных обмотках генератора.

Разработаны алгоритмы получения необходимых для реализации моделей СГ в фазных координатах функциональных зависимостей индуктивностей и взаимных индуктивностей различных обмоток по справочной информации о параметрах и характеристиках, приводимых для обеспечения расчетов динамики по уравнениям Парка – Горева.
Практические результаты.
Математическая модель СГ в фазных координатах практически реализована в среде отечественного программного комплекса «Моделирование в технических устройствах» (ПК «МВТУ») с элементами анимации и визуализации.

Результаты проведенных на созданной компьютерной модели многочисленных вычислительных экспериментов подтвердили ее практическую пригодность для расчетов динамики сложных аварийных режимов. В частности, исследован ряд аварийных режимов работы СГ, включая короткие замыкания различных видов и обрывы электрических связей в обмотках генератора, отказы в регуляторах напряжения и частоты, которые не поддаются изучению по уравнениям Парка - Горева.

Сформулированы направления дальнейших исследований с использованием моделей СГ в фазных координатах в интересах расследования причин и хода развития каскадных аварий в ЭЭС и разработки алгоритмов противоаварийного управления.