Счётчики

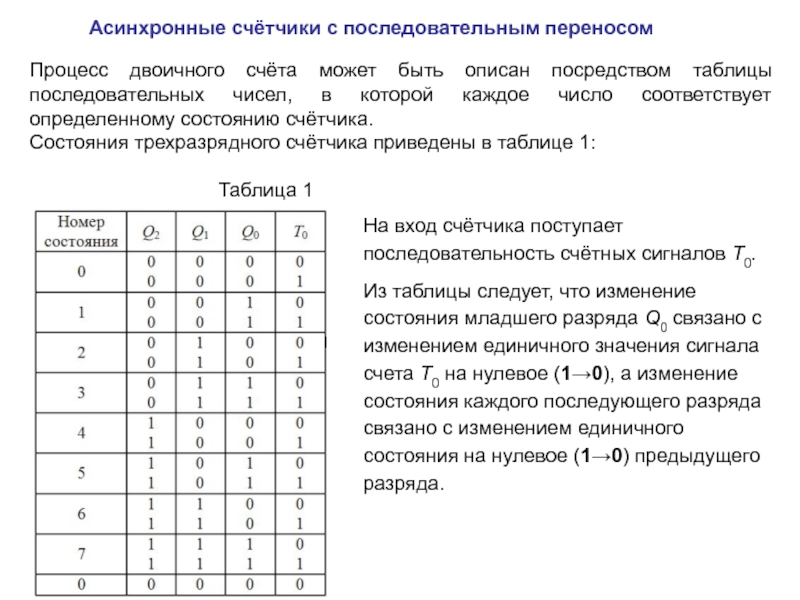
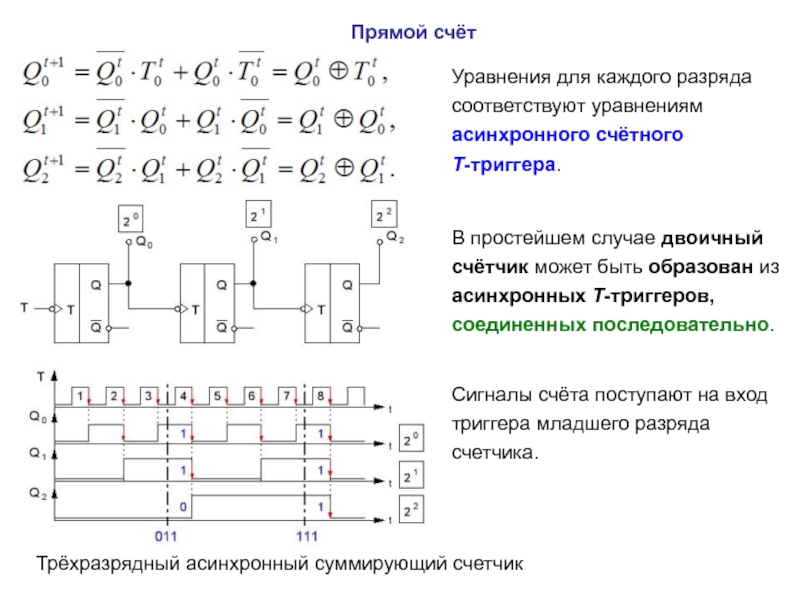
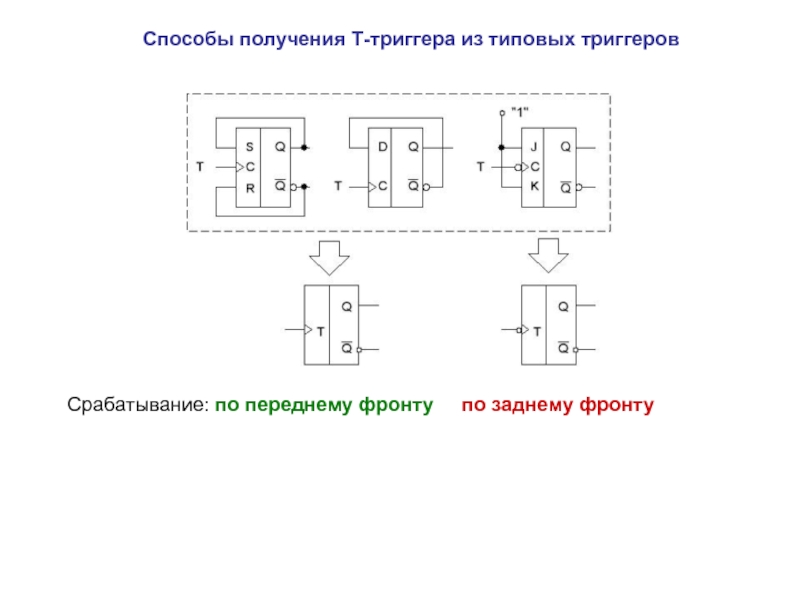
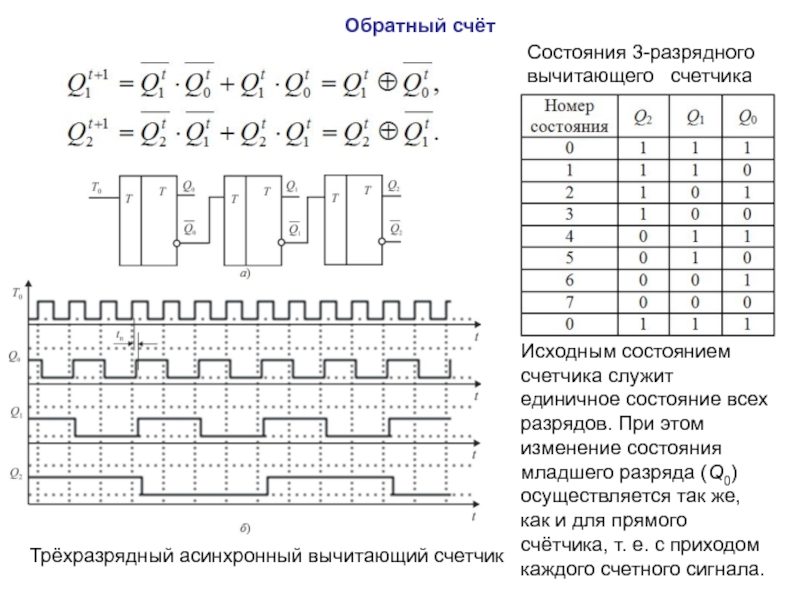
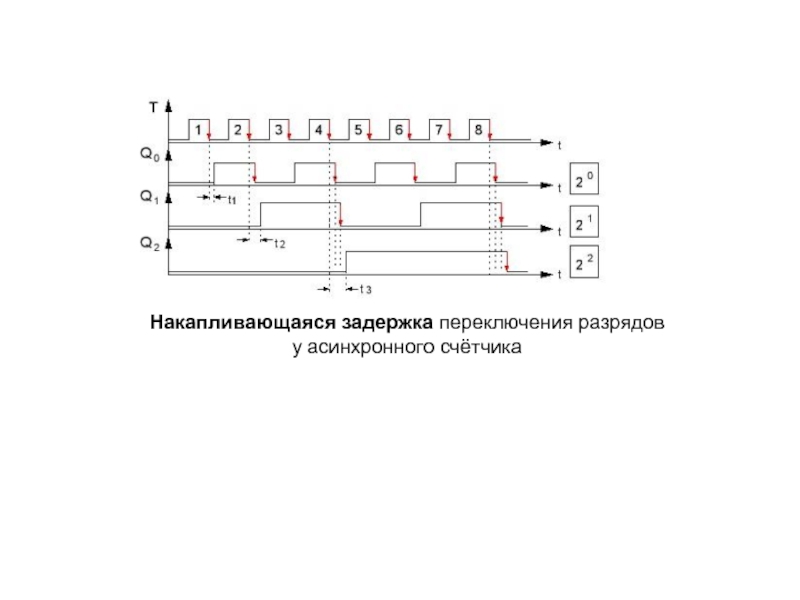
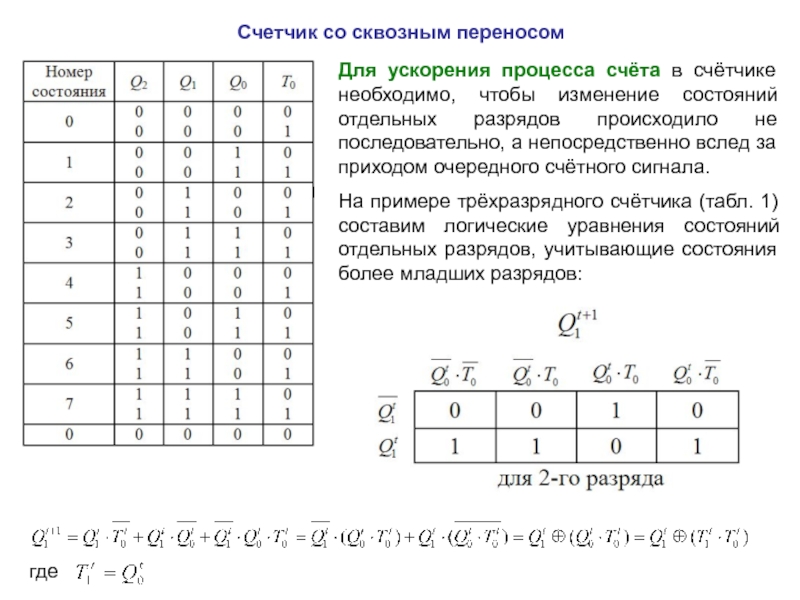
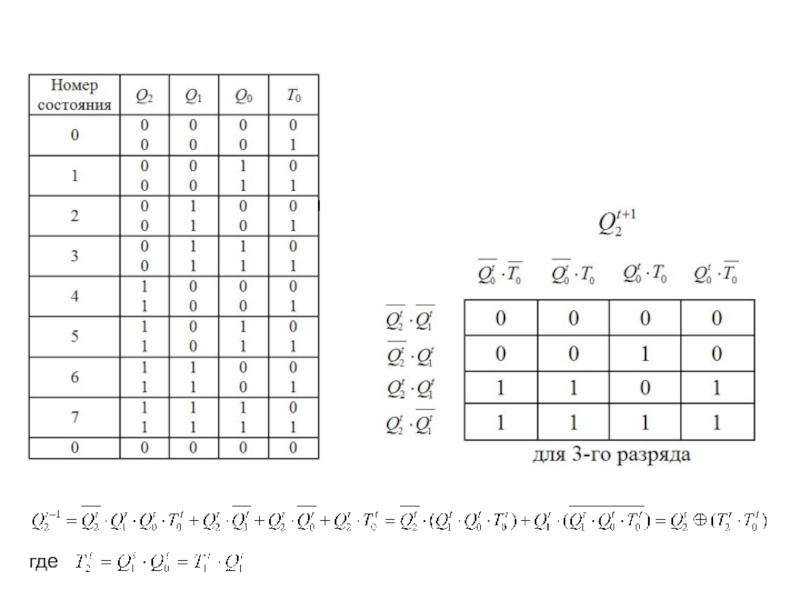
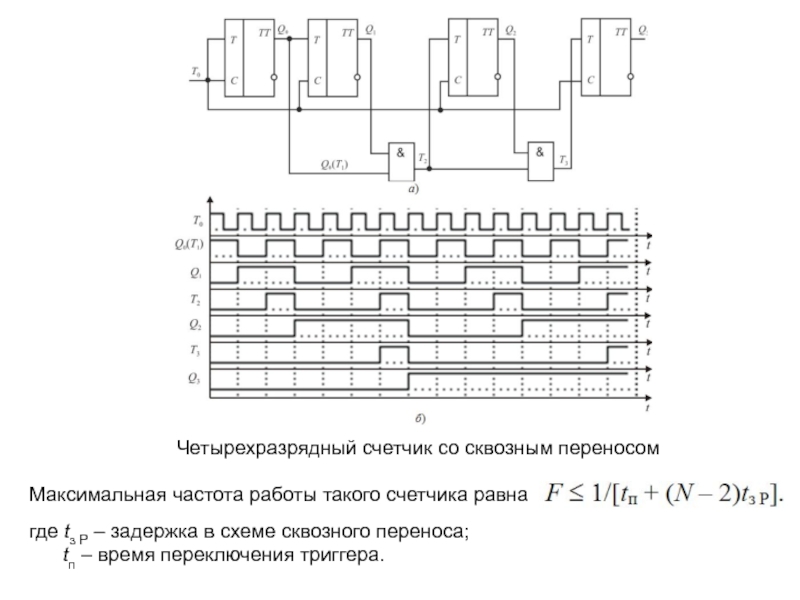
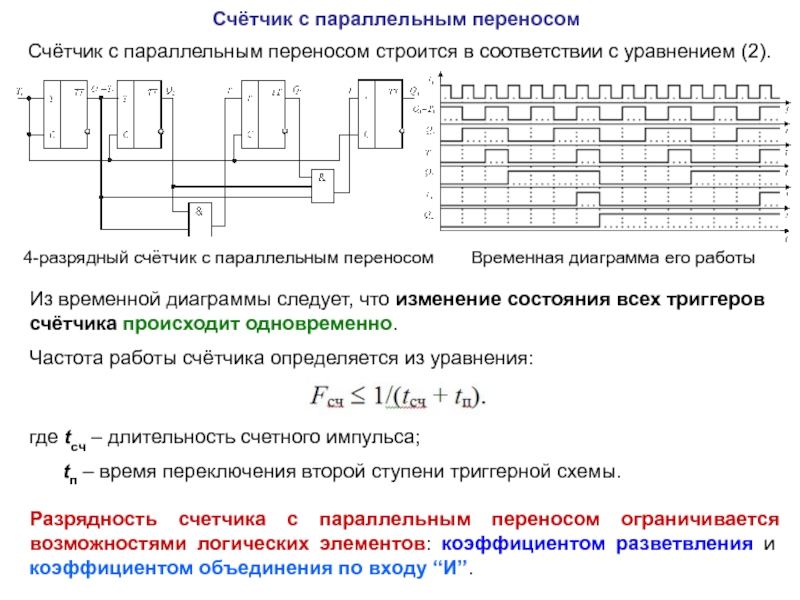
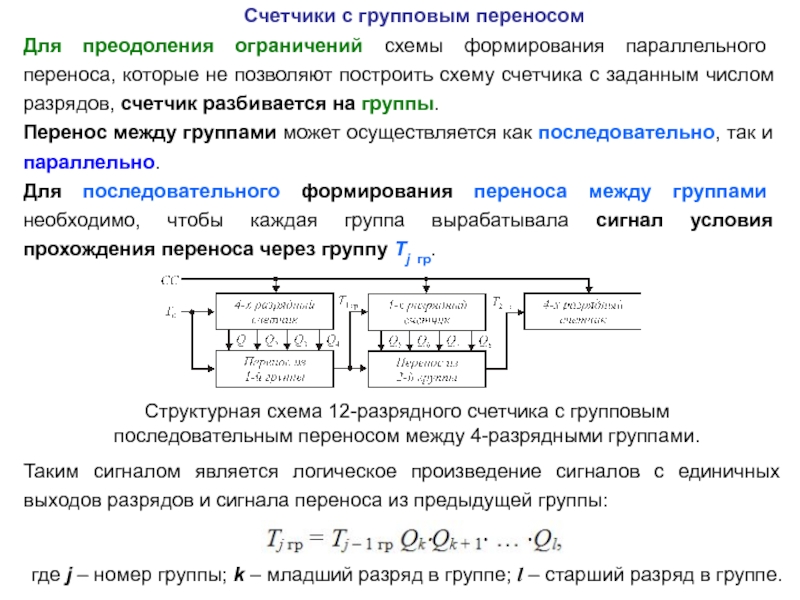
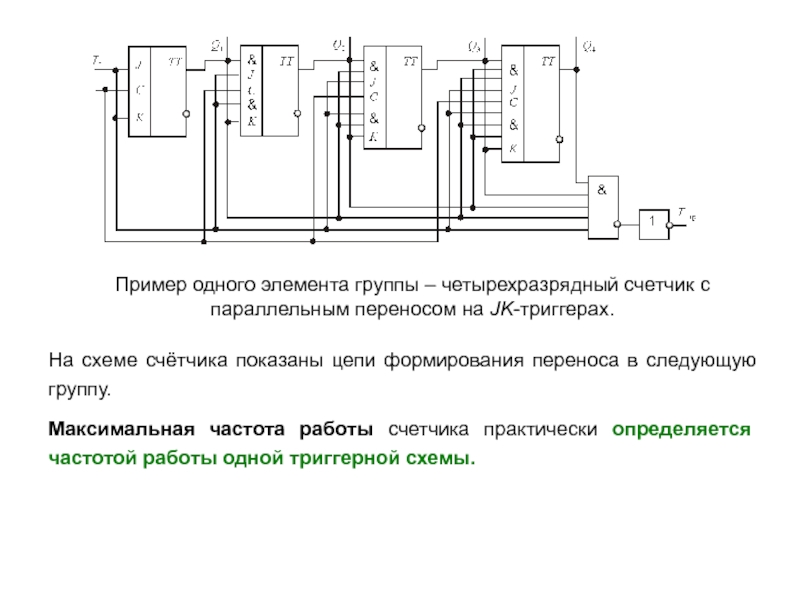
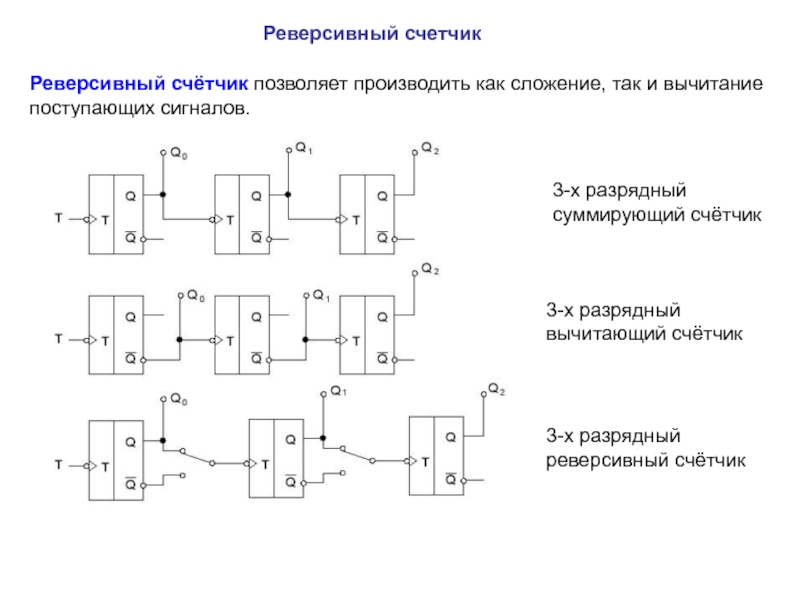
описан посредством таблицы последовательных чисел, в которой каждое число соответствует

определенному состоянию счётчика.
Состояния трехразрядного счётчика приведены в таблице 1:

На вход счётчика поступает последовательность счётных сигналов Т0.
Из таблицы следует, что изменение состояния младшего разряда Q0 связано с изменением единичного значения сигнала счета Т0 на нулевое (1→0), а изменение состояния каждого последующего разряда связано с изменением единичного состояния на нулевое (1→0) предыдущего разряда.

Таблица 1

T-триггера.

В простейшем случае

двоичный счётчик может быть образован из асинхронных Т-триггеров, соединенных последовательно.


Сигналы счёта поступают на вход триггера младшего разряда счетчика.

Трёхразрядный асинхронный суммирующий счетчик

по заднему фронту

всех разрядов. При этом изменение состояния младшего разряда (Q0) осуществляется

так же, как и для прямого счётчика, т. е. с приходом каждого счетного сигнала.

Состояния 3-разрядного вычитающего счетчика

частотой переключения его младшего разряда.
Для двухступенчатых триггерных схем, на

которых обычно строятся Т-триггеры, частота следования сигналов счета составляет:

где tсч – длительность счётного импульса; tп – время переключения второй ступени триггерной схемы.

Числа, формируемые счётчиком, могут быть выведены из него в параллельной форме посредством одновременного опроса состояния всех разрядов счётчика. Такой опрос может происходить только в паузе между сигналами счёта, т. е. после того, как завершился переходной процесс, связанный с переключением триггерных схем.
В этом случае минимальный период следования счётных импульсов должен быть увеличен на время, необходимое для полного переключения всех N разрядов счетчика и опроса его состояния:

где tопр − длительность сигнала опроса.

необходимо, чтобы изменение состояний отдельных разрядов происходило не последовательно, а

непосредственно вслед за приходом очередного счётного сигнала.
На примере трёхразрядного счётчика (табл. 1) составим логические уравнения состояний отдельных разрядов, учитывающие состояния более младших разрядов:

где

которого построены в соответствии с уравнениями (1), носит название счетчик

со сквозным переносом.
Такой счетчик может быть построен на синхронных Т-триггерах.
При этом на синхронизирующий вход этих триггеров заводится счетный сигнал Т0, а на счетные входы – сигнал Ti.

(1)

(2)

задержка в схеме сквозного переноса;
tп –

время переключения триггера.

Четырехразрядный счетчик со сквозным переносом

с уравнением (2).
4-разрядный счётчик с параллельным переносом
Временная диаграмма его работы
Из

временной диаграммы следует, что изменение состояния всех триггеров счётчика происходит одновременно.
Частота работы счётчика определяется из уравнения:

где tсч – длительность счетного импульса;
tп – время переключения второй ступени триггерной схемы.

Разрядность счетчика с параллельным переносом ограничивается возможностями логических элементов: коэффициентом разветвления и коэффициентом объединения по входу “И”.

построить схему счетчика с заданным числом разрядов, счетчик разбивается на

группы.
Перенос между группами может осуществляется как последовательно, так и параллельно.
Для последовательного формирования переноса между группами необходимо, чтобы каждая группа вырабатывала сигнал условия прохождения переноса через группу Тj гр.

Счетчики с групповым переносом

где j – номер группы; k – младший разряд в группе; l – старший разряд в группе.

Таким сигналом является логическое произведение сигналов с единичных выходов разрядов и сигнала переноса из предыдущей группы:

Структурная схема 12-разрядного счетчика с групповым последовательным переносом между 4-разрядными группами.

на JK-триггерах.
На схеме счётчика показаны цепи формирования переноса в следующую

группу.
Максимальная частота работы счетчика практически определяется частотой работы одной триггерной схемы.

формируется, как логическое произведение счетного сигнала Т0 и сигналов с

единичных выходов всех предшествующих разрядов:

Максимальная частота счетчика с одновременным переносом определяется соотношением:

Структурная схема 12-разрядного счетчика с параллельным групповым переносом между 4-разрядными группами.

где Qi – сигнал с единичного выхода старшего разряда.

поступающих сигналов.
3-х разрядный суммирующий счётчик
3-х разрядный вычитающий счётчик
3-х разрядный

реверсивный счётчик

в виде дополнения до 2N, где N – число разрядов

в счетчике.

Четырёхразрядный реверсивный счетчик с последовательным переносом

Для реализации механизма коммутации сигналов применяется дополнительная комбинационная схема.

выпускаемые в виде ИС, имеют помимо основных выходов – дополнительные,

обозначаемые, например, “≥9“, “≥15”, “≤0”.
Сигнал “1” появляется на этом выходе при заполнении счётчика. Следовательно, на этом выходе формируется сигнал переноса в следующий счётчик. На другом выходе “≤0”, сигнал появляется при заполнении счётчика “0” и является сигналом займа из предыдущего счётчика в режиме вычитания.