Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сіденко Володимир Павлович, Старший викладач кафедри “Безпека інформаційних та
Содержание
- 1. Сіденко Володимир Павлович, Старший викладач кафедри “Безпека інформаційних та
- 2. Сіденко Володимир Павлович,Старший викладач кафедри “Безпека інформаційних
- 3. Лекція № 19ПРИНЦИПИ ПОБУДОВИ АЛГОРИТМІВ АСИМЕТРИЧНОГОШИФРУВАННЯ ДАНИХ3
- 4. Питання лекції № 19 1. Принципи шифрування даних
- 5. 51. ПРИНЦИПИ ШИФРУВАННЯ ДАНИХ ЗА ДОПОМОГОЮ АСИМЕТРИЧНИХ КРИПТОГРА-ФІЧНИХ СИСТЕМ
- 6. 6 Нагадаємо, що в симетричній крипто- графії кожна
- 7. 7Рис. 19.1. Узагальнена схема криптографічної системи з
- 8. 8 Розв'язок цих задач (використання криптографічних систем з
- 9. 9 Розшифрувати послане повідомлення зможе тільки той, у
- 10. 10при якій інформація про відкритий ключ ніяк
- 11. 11 Але тільки рік по тому була опубліко-
- 12. 12 Перетворення, що володіє зазначеною властивістю, називається однобічною
- 13. 13 У наступнім питанні, випереджаючи розповідь про
- 14. 14 Висновки При використанні симетричної крипто- графії кожна зі
- 15. 152. ОДНОБІЧНІ ФУНКЦІЇ В АСИМЕТРИЧНИХ КРИПТОГРАФІЧНИХ СИСТЕМАХ
- 16. 16 Найбільш важлива однобічна функція, використовувана в криптографії
- 17. 17певна на кінцевій множині X (x €
- 18. 18 Дане визначення, безумовно, нефор- мально. Строге визначення
- 19. 19і називається дискретним логарифмом. Для того щоб забезпечити
- 20. 20 Почнемо із прикладу обчислення чис- ла а16
- 21. 21 У ряді (19.5) кожне число виходить шляхом
- 22. 22 Усі обчислення проводяться по моду- лю р. Приклад.
- 23. 23 Нам треба було всього 8 операцій мно-
- 24. 24приклад). З умови t = | log x
- 25. 25 Важливо відзначити, що настільки ж ефективні алгоритми
- 26. 26Таблиця 19.1Кількість множень для обчислення прямій і зворотної функції
- 27. 27 Ми бачимо, що якщо використовувати модулі, що
- 28. 28TОБЧ.ОБР = 2∙1045∙10-14 = 1031 сек.,тобто більш
- 29. 29операцій багато більше 2∙log p. Таким чином, можна
- 30. 30 Основні вимоги до однобічних функ- цій: - пряме
- 31. 313. КРИПТОГРАФІЧНА СИСТЕМА ЗВІДКРИТИМ КЛЮЧЕМДИФФИ-ХЕЛЛМАНА
- 32. 32 Ця криптосистема була відкрита в се- редині
- 33. 33 Нехай ми прагнемо організувати сек- ретний зв'язок
- 34. 34 Ми бачимо, що при великому числі абонентів
- 35. 381 < g < р - 1,таке,
- 36. 36 Кожний абонент обчислює відповідне число Y, яке відкрито передається іншим абонентам, У результаті одержуємо наступну таб- лицю.
- 37. 37Таблиця 19.2Ключі користувачів у системі Диффи-Хеллмана Допустимо, абонент
- 38. 38 Потім абонент А обчислює величину Ніхто іншої крім
- 39. 39 Тут перша рівність випливає з (19.10), друге
- 40. 40ливо (потрібні тисячі років)). Абоненти A і В
- 41. 41системи число р-1 повинне обов'язково містити великий
- 42. 42і Приклад. Нехай р = 23 = 2∙11
- 43. 43 Тепер кожний абонент вибирає секрет- не число
- 44. 44ZBA = 1713 mod 23 = 10. Тепер
- 45. 45 По-друге, дана система по суті явилася початком розвитку криптографічних систем з відкритими ключами.
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Сіденко Володимир Павлович,
Старший викладач кафедри “Безпека інформаційних та комунікаційних систем”
1
ЗМІСТОВНИЙ
МОДУЛЬ № 4
Слайд 2Сіденко Володимир Павлович,
Старший викладач кафедри “Безпека інформаційних та комунікаційних систем”
2
Тема
№ 8
ПРИНЦИПИ ПОБУДОВИ АЛГОРИТМІВ АСИМЕТРИЧНОГО ШИФРУВАННЯ. АЛГОРИТМ RSA
Слайд 4Питання лекції № 19
1. Принципи шифрування даних за допомогою асиметричних
криптогра- фічних систем
2. Однобічні функції в асиметрич- них криптографічних системах
3.
Криптографічна система з від- критим ключем Диффи-ХеллманаЛітература: Л3, с. 128 – 131.
4
Слайд 66
Нагадаємо, що в симетричній крипто- графії кожна зі сторін, яка
обмінюється по- відомленнями, повинна мати копію загаль- ного секретного ключа,
що створює най- складнішу проблему керування ключами.Сьогодні ці проблеми вирішуються з використанням криптографічних систем з асиметричними (відкритими) ключами. У таких криптографічних системах, про яких піде мова далі, використовуються два клю- чі: відкритий і секретний (рис. 19.1).
Слайд 77
Рис. 19.1. Узагальнена схема криптографічної системи з відкритим ключем
Розв'язок
цих задач (використання криптографічних систем з відкритим і сек- ретним
ключем) засноване на важливім понятті однобічної функції (one-way function).Слайд 88
Розв'язок цих задач (використання криптографічних систем з відкритим і сек-ретним
ключем) засноване на важливім понятті однобічної функції (one-way func tion).
Відкритий
ключ може бути опубліко- ваний у довіднику поряд з іменем корис- тувача. У результаті будь-який бажаючий може зашифрувати з його допомогою свій лист і послати закриту інформацію влас- никові відповідного секретного ключа.Слайд 99
Розшифрувати послане повідомлення зможе тільки той, у кого є секретний
ключ, яким-небудь образом пов'язаний із цим відкритим ключем.
Таким чином, кожний
може послати одержувачеві секретну інформацію, ско- риставшись його відкритим ключем. Але тільки одержувач у стані розшифрувати повідомлення, оскільки лише в нього є відповідний секретний ключ.Причина працездатності таких крипто- систем полягає в однобічному математич- ному зв'язку, що існує між двома ключами,
Слайд 1010
при якій інформація про відкритий ключ ніяк не допомагає відновити
секретний, але володіння секретним ключем забезпечує можливість розшифровувати повідомлен- ня,
зашифровані за допомогою відкритого ключа.На перший погляд такий зв'язок ви- дасться дивним, і для його розуміння пот- рібне певний час і розумовий зусилля.
Ідея криптографії з відкритим ключем уперше з'явилася в 1976 р. у революційній роботі Диффи й Хеллмана “Нові напрямки в криптографії”.
Слайд 1111
Але тільки рік по тому була опубліко- вана перша (і
найбільш успішна) крипто- графічна система з відкритим ключем, а саме,
RSA.Мала кількість ідей пояснюється необ-хідністю знайти яке-небудь легко здійс-ненне на стадії шифрування математичне перетворення, яке складно було б звернути (без знання спеціальної секретної інфор-мації) для реалізації другої стадії алго-ритму, тобто розшифрування.
Слайд 1212
Перетворення, що володіє зазначеною властивістю, називається однобічною фун- кцією або
функцією-пасткою, оскільки в її двері ввійти легко (зашифрувати дані), а
от вийти без ключа досить проблематично.Придумати таку функцію на порожньо- му місці досить непросто, але, на щастя, є деякий набір широко відомих і всебічно ви- вчених однобічних функцій. До них став- ляться задача розкладання цілих чисел на множники, проблема обчислення дискрет- них логарифмів або обчислення квадрат- ного корінь по модулю складеного числа.
Слайд 1313
У наступнім питанні, випереджаючи розповідь про алгоритми шифрування з
відкритим ключем, ми познайомимося із прикладами однобічних функцій. Однак во-
ни є однобічними тільки в обчислюваль- вальному відношенні, тобто маючи досить більші комп'ютерні потужності, їх цілком можна звернути, причому швидше, чим знайти секретний ключ у результаті повно- го перебору.Слайд 1414
Висновки
При використанні симетричної крипто- графії кожна зі сторін повинна мати
копію загального секретного ключа, що створює найскладнішу проблему керування ключа-
ми.Сьогодні ці проблеми вирішуються з використанням криптографічних систем з асиметричними (відкритими) ключами. У таких криптографічних системах, викорис- товуються два ключі: відкритий і секрет- ний.
Слайд 1616
Найбільш важлива однобічна функція, використовувана в криптографії з відкри- тим
ключем, - це розкладання на множники або факторізація цілих чисел
та дискретне логарифмування.Під розкладанням на множники цілого числа розуміють його представлення у виг- ляді добутку простих дільників, наприклад,
10 = 2 * 5,
60 = 22 * 3 * 5,
2113 - 1 =
3391*23279*65993*1868569*1066818*132868207.
Нехай дана функція
Слайд 1717
певна на кінцевій множині X (x € X), для якої
існує зворотна функція
Функція називається однобічної, якщо обчислення по формулі (19.1)
- проста за- дача, що вимагає небагато часу, а обчис- лення по (19.2) - задача складна, що вима- гає залучення маси обчислювальних ре- сурсів, наприклад, 106 – 1010 років роботи потужного суперкомп'ютера.Слайд 1818
Дане визначення, безумовно, нефор- мально. Строге визначення однобічної функції може
бути знайдене в математич- них роботах, але для наших цілей
досить і вищенаведеного.Як приклад однобічної функції розгля-немо наступну:
де р - деяке простої число (тобто таке, яке ділиться без остачі тільки на себе й на оди- ницю), а х - ціле число із множини {1, 2, 3, …, p-1}. Зворотна функція позначається
Слайд 1919
і називається дискретним логарифмом.
Для того щоб забезпечити труднощі обчислення по
(19.4) при використанні кра- щих сучасних комп'ютерів, у цей час
вико- ристовуються числа розміром більш 512 біт. На практиці часто застосовуються й інші однобічні функції, наприклад, так звані хеш-функції, що оперують із суттєво більш короткими числами порядку 128-256 біт.Спочатку ми покажемо, що обчислення (19.3) може бути виконане досить швидко.
Слайд 2020
Почнемо із прикладу обчислення чис- ла а16 mod p. Ми
можемо записати
а16 mod p = ((((a2) * a2 ) *
a2) * a2) mod p ,тобто значення даної функції обчислюєть- ся всього за 4 операції множення замість 15 при “наївному” варіанті а * а * … * a.
На цьому заснований загальний алго- ритм.
Для опису алгоритму введемо величи- ну t = | log2x | - цілу частину log2x (далі всі логарифми будуть двійкові, тому надалі ми не будемо вказувати основу 2).
Слайд 2121
У ряді (19.5) кожне число виходить шляхом множення попереднього числа
са- мого на себе по модулю р.
Запишемо показник ступеня х
у двійко-вій системі числення:x = ( xt xt-1 xt-2 xt-3 … x1 x0 )2 .
Тоді число y = ах mod p може бути об-числене як
Обчислюємо числа ряду
Слайд 2222
Усі обчислення проводяться по моду- лю р.
Приклад. Нехай потрібно обчислити
3100 mod 7. Маємо t = | log 100 |
= 6. Обчис- люємо числа ряду (19.5): Записуємо показник у двійковій систе- мі числення:
100 = (1100100)2
і проводимо обчислення по формулі (19.6):
Слайд 2323
Нам треба було всього 8 операцій мно- ження (6 для
обчислення ряду (19.7) і 2 для (19.8)). У загальному випадку
справедливо наступне.Твердження (про складність обчис- лень (19.3)). Кількість операцій множення при обчисленні (19.3) по описаному методу не перевершує 2 log х.
Доказ. Дня обчислення чисел ряду (19.5) потрібно t множень, для обчислення y по (19.6) не більш, ніж t множень (див.
Слайд 2424
приклад).
З умови t = | log x |, враховуючи, що
|log
x| ≤ log x,
робимо висновок про справедливість до- казуваного твердження.
3ауваження.
Як буде показано надалі, при піднесенні в ступінь по модулю p має сенс використовувати тільки показники х < р. У цьому випадку ми можемо сказати, що кількість операцій множення при обчислен- ні (19.3) не перевершує 2 log p.Слайд 2525
Важливо відзначити, що настільки ж ефективні алгоритми обчислення зворот-ної функції
(19.4) невідомі.
Один з методів обчислення (19.4), на- зиваний “крок дитини,
крок велетня”, ви- магає порядку 2∙р1/2 операцій.Покажемо, що при більших р функція (19.3) дійсно однобічна, якщо для обчис- лення зворотної функції використовується метод “крок дитини, крок велетня”.
Одержуємо наступний результат (табл. 19.1).
Слайд 2727
Ми бачимо, що якщо використовувати модулі, що складаються із 50-100
десятко- вих цифр, те “пряма” функція обчислюєть- ся швидко, а
зворотна практично не обчис- люємо.Розглянемо, наприклад, суперкомп'ю- тер, який множить два 90-значных числа за 10-14 сек (для сучасних комп'ютерів це поки не доступно). Для обчислення (19.3) такому комп'ютеру буде потрібно
TОБЧ.ПР = 600∙10-14 = 6∙10-12 сек.,
а для обчислення (19.4)
Слайд 2828
TОБЧ.ОБР = 2∙1045∙10-14 = 1031 сек.,
тобто більш 1023 років. Ми
бачимо, що об- числення зворотних функції практично не- можливо при
довжині чисел порядку 90 де- сяткових цифр, і використання паралель- них обчислень і комп'ютерних мереж суттє- во не міняє ситуацію. У розглянутому прик- ладі ми припускали, що зворотна функція обчислюється за 2∙р1/2 операцій. У цей час відомі й більш “швидкі” методи обчислен- ня дискретного логарифма, однак загальна картина та ж - кількість необхідних у нихСлайд 2929
операцій багато більше 2∙log p.
Таким чином, можна затверджувати, що функція
(19.3) дійсно однобічна, але із застереженням. Ніким не доведене, що
зво- ротна функція (19.4) не може бути обчисле- на настільки ж швидко, як і “пряма”.Висновки
Криптографічні системи з асиметрич- ними (відкритими) ключами вирішують проблему розподілу ключів, але потрі- бують використання однобічних функцій.
Слайд 3030
Основні вимоги до однобічних функ- цій:
- пряме обчислення повинно здійсню-
ватися швидко;
- зворотне обчислення без знання секретного ключа неможливо або
для її об- числення потребується досить багато часу.Слайд 3232
Ця криптосистема була відкрита в се- редині 70-х років американськими
вченими Диффи (Whitfield Diffie) і Хеллманом (Martin Hellman) і привела
до справжньої револю- ції в криптографії і її практичних застосу- ваннях. Це перша система, яка дозволяла захищати інформацію без використання секретних ключів, переданих по захищених каналах. Для той щоб продемонструвати одну зі схем застосування таких систем, розглянемо мережу зв'язку з N користува- чами, де N - велике число.Слайд 3333
Нехай ми прагнемо організувати сек- ретний зв'язок для кожної пари
з них. Якщо ми будемо використовувати звичайну сис- тему розподілу
секретних ключів, то кожна пара абонентів повинна бути постачена своїм секретним ключем, тобто всього бу- де потрібноключів.
Якщо абонентів 100, то потрібно 5000 ключів, якщо ж абонентів 104, то ключів повинне бути 5∙107.
Слайд 3434
Ми бачимо, що при великому числі абонентів система постачання їх
секретни- ми ключами стає дуже громіздкої й доро- гою.
Диффи й
Хеллман розв'язали цю проб- лему за рахунок відкритого поширення й обчислення ключів. Перейдемо до опису запропонованої ними системи.Нехай будується система зв'язку для абонентів A, B, C, ... . У кожного абонента є своя секретна й відкрита інформації. Для організації цієї системи вибирається вели- ке просте число р і деяке число g,
Слайд 3538
1 < g < р - 1,
таке, що всі числа
із множини {1,2, …, р - 1} можуть бути представлені
як різні ступені g mod р (відомі різні підходи для знаходжен- ня таких чисел g, один з них буде пред- ставлений нижче).Числа р і g відомі всім абонентам.
Абоненти вибирають більші числа ХA, ХB, ХC, … які зберігають у секреті (звичайно такий вибір рекомендується проводити ви- падково, використовуючи датчики випад- кових чисел).
Слайд 3636
Кожний абонент обчислює відповідне число Y, яке відкрито передається іншим
абонентам,
У результаті одержуємо наступну таб- лицю.
Слайд 3737
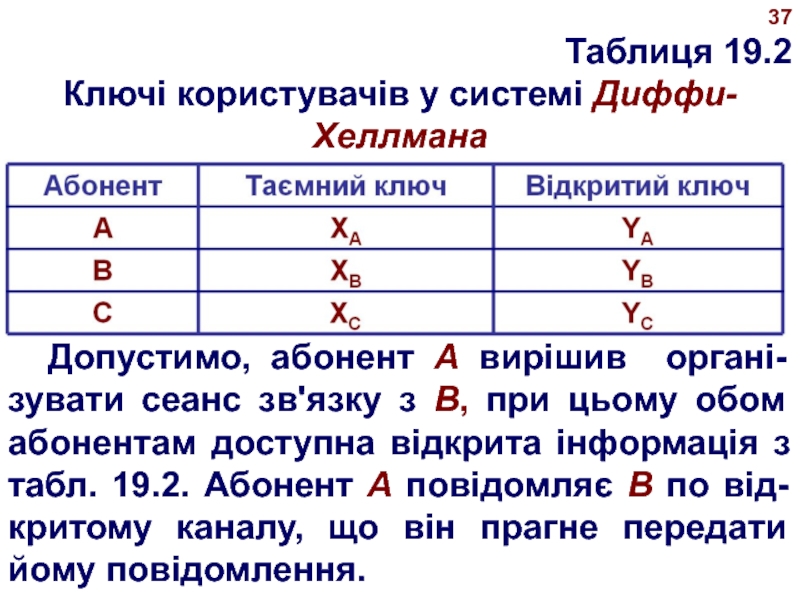
Таблиця 19.2
Ключі користувачів у системі Диффи-Хеллмана
Допустимо, абонент А вирішив органі-
зувати сеанс зв'язку з В, при цьому обом абонентам доступна
відкрита інформація з табл. 19.2. Абонент А повідомляє В по від- критому каналу, що він прагне передати йому повідомлення.Слайд 3838
Потім абонент А обчислює величину
Ніхто іншої крім А цього зробити
не мо- же, тому що число ХA секретне. У свою
чер- гу, абонент В обчислює число Твердження. ZAB = ZBA.
Доказ. Дійсно,
Слайд 3939
Тут перша рівність випливає з (19.10), друге й четверте –
з (19.9), останнє - з (19.11).
Відзначимо головні властивості систе-
ми:- абоненти А і В одержали те саме чис- ло Z = ZAB = ZBA, яке не передавалося по відкритій лінії зв'язку;
- зловмисник не знає секретних чисел ХA, ХB,..., тому не може обчислити число Z (загалом кажучи, він міг би спробувати знайти секретне число ХA по YA (див. (19.9)), однак при більших р це практично немож-
Слайд 4040
ливо (потрібні тисячі років)).
Абоненти A і В можуть використову- вати
Z у якості секретного ключа для шиф- рування й розшифрування
даних. У такий же спосіб будь-яка пара абонентів може обчислити секретний ключ, відомий тільки їм.Зупинимося тепер на згаданої вище задачі вибору числа g. При довільно зада- ному р вона може виявитися важкою зада- чею, пов'язаної з розкладанням на прості множники числа р-1. Справа в тому, що для забезпечення високої стійкості розглянутої
Слайд 4141
системи число р-1 повинне обов'язково містити великий простий множник, а
якщо ні, то алгоритм Полига-Хеллмана, швидко обчислює дискретний логарифм. Тому
час- то рекомендують використовувати наступ- ний підхід. Просте число р вибирається та- ким, щоб виконувалася рівністьр = 2∙q – 1,
де q - також просте число. Тоді в якості g можна обрати будь-яке число, для якого виконуються нерівності
Слайд 4242
і
Приклад. Нехай р = 23 = 2∙11 + 1 (q
= 11). Виберемо параметр g. Спробуємо обрати g = 3.
Перевіримо:
311
mod 23 = 1і виходить, таке g не підходить. Оберемо g = 5. Перевіримо:
511 mod 23 = 22.
Отже, ми вибрали параметри р = 23, g = 5.
Слайд 4343
Тепер кожний абонент вибирає секрет- не число й обчислює відповідне
йому від- крите число. Нехай обрані ХA = 7, ХB
= 13.Обчислюємо
YA = 57 mod 23 = 17, YB = 513 mod 23 = 21.
Нехай A і В вирішили сформувати за- гальний секретний ключ. Для цього А об- числює
ZAB = 217 mod 23 = 10,
а В обчислює
Слайд 4444
ZBA = 1713 mod 23 = 10.
Тепер вони мають загальний
ключ 10, який не передавався по каналу зв'язку.
Висновки
Пропонована криптографічна система
американськими вченими Диффи і Хеллма- ном привела до справжньої революції в криптографії і її практичних застосуваннях.По-перше, ця система дозволила захи- щати інформацію без пересилання секрет- них ключів.