Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Семей қаласы ф изика - математика бағытындағы Назарбаев Зияткерлік
Содержание
- 1. Семей қаласы ф изика - математика бағытындағы Назарбаев Зияткерлік
- 2. Бүгін біз көпмүшені көпмүшеге көбейтуде кейбір жағдайларды
- 3. Бүгін біз көпмүшені көпмүшеге көбейтуде кейбір жағдайларды
- 4. Қысқаша көбейту формулаларын меңгеріп, оларды алгебралық өрнектерді
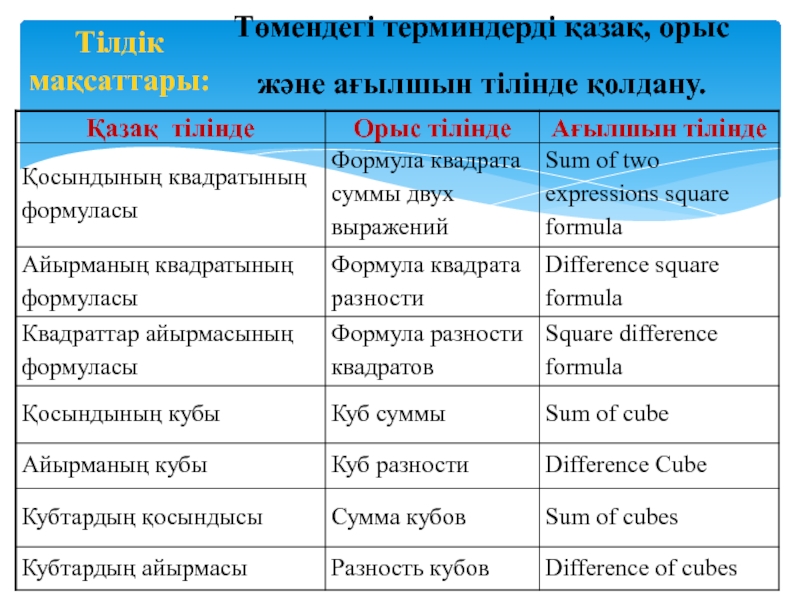
- 5. Тілдік мақсаттары:Төмендегі терминдерді қазақ, орыс және ағылшын тілінде қолдану.
- 6. Слайд 6
- 7. Слайд 7
- 8. Бірмүше одночлены monomialСандардан, айнымалылардан және олардың
- 9. Көбейтіндіні табыңыз
- 10. (a+b)2 = (a+b)(a+b) = =a·a +a·b +
- 11. Екі өрнектің айырымының квадраты (a-b)2 = (a-b) (a-b) =(2)
- 12. (a-b)2=a2-2ab+b 2Екі өрнектің айырымының квадраты Екі
- 13. (a b)2 = a 2
- 14. (a b)2 = a 2
- 15. Көпмүше түріне келтіріңіздер1-мысал.
- 16. 9 –ға тең5 –ке тең (a
- 17. аbааbbаb S=ab S=abГеометриялық мағынасы
- 18. аbааbbаb S=ab
- 19. Қосындының квадраты немесе айырманың квадраты формуласын қолдану
- 20. Қосындының квадраты немесе айырманың квадраты формуласын қолдану
- 21. Екі өрнектің квадраттарының айырымының формуласы(a+b)(a-b)= (a-b) айырмасын (a+b) қосындысына көбейтейік:
- 22. Екі өрнектің квадраттарының айырымының формуласы(a+b)(a-b) =a2-b2(a+b)(a-b)=
- 23. a2-b2=(a+b)(a-b)Бұл формуланы түрінде жиі қолданады. Ол екі
- 24. S- қабырғасы a- ға тең квадраттың
- 25. Мысалдар қарастырайық9-мысал.
- 26. Бұл формулаларды жылдам есептеуде қолдануға болады.1332-1342=(29-28)(29+28)292-282==1·57=57732-632=(73+63)(73-63)=136·10=1360(133-134)(133+134)=-267
- 27. Екі өрнектің қосындысының кубы.
- 28. Екі өрнектің қосындысының кубы.(4)(a+b)3=a3+3a2b+3ab2+b3Екі өрнектің қосындысының кубы
- 29. Екі өрнектің айырмасының кубы. (a-b)3=(a-b)(a-b)2= (a-b)(a2-2ab+b2)= =a3 -2a2b+ab2-ba2+2ab2-b3=a3-3a2b+3ab2-b3
- 30. Екі өрнектің айырмасының кубы.Екі өрнектің айырмасының кубы
- 31. (a b)3 = a3 3a2b
- 32. (a b)3 = a3 3a2b
- 33. Екі өрнектің кубтарының қосындысыТеңбе-теңдік екі өрнектің кубтарының
- 34. Екі өрнектің кубтарының айырмасын көбейткіштерге жіктеу үшін:(7)a3-b3= (a-b)(a2+ab+b2)
- 35. Екі өрнектің кубтарының айырмасын көбейткіштерге жіктеу үшін:Теңбе-теңдік
- 36. Мысалдар қарастырайық 15-мысал.
- 37. (a+b)3 = a3+3a2b+3ab2+b3(a-b)3 = a3 - 3a2b+3ab2
- 38. Біз қысқаша көбейту формуласын
- 39. Білімді және дағдыны бекіту 1) (х2 +
- 40. Жауаптары 1) x4 + 2x2 + 1;
- 41. Деңгейлік тапсырма. (Рационалды жолмен шешіңіз)1-тапсырма: Өрнекті ықшамдап
- 42. Жауаптары: 1-тапсырма: Өрнекті ықшамдап көбейткіштерге жіктеңіз2-тапсырма: Көпмүше
- 43. Өзіндік жұмыс.
- 44. №1 (5x+4)(25x2-20x+16)-64==(125х3+64)-64=125х3.Мұндағы х=2;
- 45. Кейбір математикалық фокустарҚосындының квадраты және айрманың квадраты
- 46. Қосындының квадраты мен айырманың квадраты формуласын қолданып есептеңіз 1) 792; 2) 212; 3) 882; 4) 982.
- 47. Жауаптары(80-1)2 =6400-160+1= 6241;(20+1)2=400+40+1= 441;(90-2)2=8100-360+4=7744;(100-2)2=10000-400+4=9604.
- 48. Оқушылар сабақтан алған әсерлері бойынша + немесе
- 49. Қолданылған әдебиеттер 1. Шыныбеков Ә.Н. Алгебра 7
- 50. Назар салып тыңдағандарыңызға рахмет!!!Сабақтың барлық материалдарын moodle.nis.edu.kz сайтынан таба аласыздар
- 51. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Семей қаласы физика - математика бағытындағы
Назарбаев Зияткерлік мектебі
Кысқаша көбейту
формулалары
Слайд 2Бүгін біз көпмүшені көпмүшеге көбейтуде кейбір жағдайларды ықшамдырақ орындауға мүмкіндік
беретін қысқаша көбейту формулалары деп аталатын формулалармен танысамыз.
Біз бұл
формулалардың дәлелдеу жолдары мен қолданылуларына мысалдар қарастырамыз. Сонымен қатар жаңа сабаққа байланысты өзін-өзі тексеруге тапсырмалар беріледі.Слайд 3Бүгін біз көпмүшені көпмүшеге көбейтуде кейбір жағдайларды ықшамдырақ орындауға мүмкіндік
беретін қысқаша көбейту формулалары деп аталатын формулалармен танысамыз.
Біз бұл
формулалардың дәлелдеу жолдары мен қолданылуларына мысалдар қарастырамыз. Сонымен қатар жаңа сабаққа байланысты өзін-өзі тексеруге тапсырмалар беріледі. Сәттілік тілеймін!
Слайд 4Қысқаша көбейту формулаларын меңгеріп, оларды алгебралық өрнектерді түрлендіруде, көпмүшені көпмүшеге
көбейту кезінде қолдана біледі және көпмүшені көбейткіштерге жіктеу тәртібін түсінеді.
Танымдық
белсенділіктерін арттыру, ұжымда жұмыс жасауын қалыптастыру. Ойлау, сөйлеу, есте сақтау қабілеттерін жетілдіру және білім дағдыларын дамыту. Осы сабақта оқылатын оқу мақсаттары
Сабақ
мақсаттары
Слайд 8 Бірмүше
одночлены
monomial
Сандардан, айнымалылардан және олардың дәрежелерінен көбейту амалы
арқылы құрастырылған өрнекті .................деп атайды.
Бірдей немесе коэффициенттері ғана өзгеше бірмүшелерді
............................ деп атайды.ұқсас мүшелер
подобный член
Identity member
Бірмүшелердің алгебралық қосындысы ..................... деп аталады
Көпмүше многочлен
polynomials
Егер жақшаның алдында ............тұрса, онда көпмүше мүшелерін өз таңбаларымен жазады.
Егер жақшаның алдында ............тұрса, онда жақша ішіндегі мүшелерді қарама-қарсы таңбалармен жазады.
Көпмүшені екі немесе бірнеше көпмүшенің көбейтіндісі түріне келтіруді ............................ деп атайды.
Плюс – plus
разложение многочленов-
decomposition of polynomials
Минус – minus
Слайд 10(a+b)2 = (a+b)(a+b) =
=a·a +a·b + b·a + b·b
=a2 +ab+ab+b2 =
=a2 +2ab +b2
Екі өрнектің қосындысының квадраты -
бірінші өрнектің квадраты, екі еселенген екі өрнектің көбейтіндісі мен екінші өрнектің квадратының қосындысына тең.
(a+b)2=a 2 + 2ab + b 2
Бұл екі өрнектің қосындысының квадратының формуласы
Жаңа сабақ
(1)
Слайд 12 (a-b)2=a2-2ab+b 2
Екі өрнектің айырымының квадраты
Екі өрнектің айырымының квадраты
- бірінші өрнектің квадраты мен екі еселенген екі өрнектің көбейтіндісі
айырмасына екінші өрнектің квадраттың қосқанға тең.
(a-b)2 = (a-b) (a-b) =
= a·a - a·b - b·a + b·b =
=a2-ab-ab+b2= a2 -2ab +b2
(2)
Слайд 15Көпмүше түріне келтіріңіздер
1-мысал.
(х+у)2=
=х2+2xy+у2
2-мысал.
(2 - 3y)2=
=4 - 12y + 9y2
3-мысал.
Слайд 18а
b
а
а
b
b
а
b
S=ab
S=ab
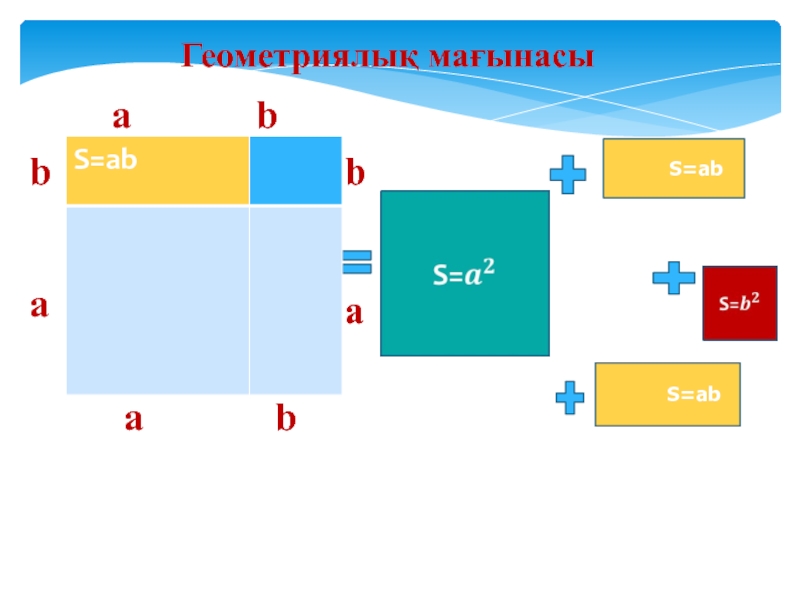
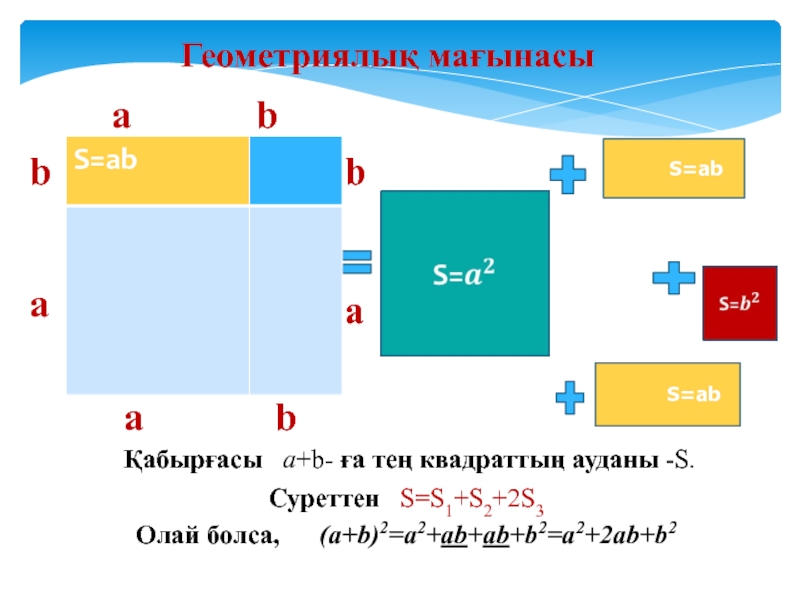
Геометриялық мағынасы
Қабырғасы a+b- ға тең квадраттың ауданы
-S. Суреттен S=S1+S2+2S3
Олай болса, (a+b)2=a2+ab+ab+b2=a2+2ab+b2
Слайд 19Қосындының квадраты немесе айырманың квадраты формуласын қолдану кезінде төмендегі жағдайды
ескеру керек,
(─a — b)² = (a + b)²;
(b — a)²
= (a — b)².Себебі: (-а)² = а²
Слайд 20Қосындының квадраты немесе айырманың квадраты формуласын қолдану кезінде төмендегі жағдайды
ескеру керек,
(─a — b)² = (a + b)²;
(b — a)²
= (a — b)².Себебі: (-а)² = а²
(15-x)2= (x-15)2
(15-x)2=225 - 30x + x2
(x-15)2 =x2 - 30x + 225.
7-мысал.
8-мысал. Тепе-теңдікті дәлелде
Слайд 21 Екі өрнектің квадраттарының айырымының
формуласы
(a+b)(a-b)=
(a-b) айырмасын (a+b) қосындысына
көбейтейік:
Слайд 22 Екі өрнектің квадраттарының айырымының
формуласы
(a+b)(a-b) =a2-b2
(a+b)(a-b)=
=a2-ab+ab-b2= a2-b2
(a-b) айырмасын
(a+b) қосындысына көбейтейік:
сонымен
Екі өрнектің айырмасының олардың қосындысына көбейтіндісі осы өрнектердің
квадраттарының айырмасына тең.Слайд 23a2-b2=(a+b)(a-b)
Бұл формуланы
түрінде жиі қолданады. Ол екі өрнектің квадраттарының айырмасын
көбейткіштерге жіктеу формуласы деп аталады
Екі өрнектің квадраттарының айырмасы осы
өрнектердің айрмасы мен қосындысының көбейтіндісіне тең.(3)
Слайд 24S- қабырғасы a- ға тең квадраттың ауданы.
Суреттен S=S1+S2+2S3
Олай
болса,
a2=b2+(a-b)2+2(a-b)b
a2-b2=(a-b)(a-b+2b)
a2-b2=(a-b)(a+b)
Геометриялық мағынасы
Дәлелденді a2-b2=(a-b)(a+b)
Слайд 25Мысалдар қарастырайық
9-мысал.
(3x+4)(3x-4)=
=9x2-16
10-мысал.
(2-5n)(5n+2)=
=4-25n2
11-мысал.
25-36b4d2=
=(5-6b2d)(5+6b2d)
12-мысал.
(x -у )(х+у)(х2+у2)=
(x2-у2)(х2+у2)=
=x4-у4
Слайд 26 Бұл формулаларды жылдам есептеуде қолдануға болады.
1332-1342=
(29-28)(29+28)
292-282=
=1·57=57
732-632=
(73+63)(73-63)=
136·10=1360
(133-134)(133+134)=
-267
Слайд 28Екі өрнектің қосындысының кубы.
(4)
(a+b)3=a3+3a2b+3ab2+b3
Екі өрнектің қосындысының кубы бірінші өрнектің кубына,
плюс бірінші өрнектің квадраты мен екінші өрнектің үш еселенген көбейтіндісіне,
плюс бірінші өрнек пен екінші өрнектің квадраттарының үш еселенген көбейтіндісіне, плюс екінші өрнектің кубына тең. (a+b)3=(a+b)(a+b)2=
(a+b)(a2+2ab+b2)=
=a3 +2a2b+ab2+ba2+2ab2+b3=
a3+3a2b+3ab2+b3
Слайд 29Екі өрнектің айырмасының кубы.
(a-b)3=(a-b)(a-b)2=
(a-b)(a2-2ab+b2)=
=a3 -2a2b+ab2-ba2+2ab2-b3=
a3-3a2b+3ab2-b3
Слайд 30Екі өрнектің айырмасының кубы.
Екі өрнектің айырмасының кубы бірінші өрнектің кубына,
минус бірінші өрнектің квадраты мен екінші өрнектің үш еселенген көбейтіндісіне,
плюс бірінші өрнек пен екінші өрнектің квадраттарының үш еселенген көбейтіндісіне, минус екінші өрнектің кубына тең.(5)
(a-b)3=(a-b)(a-b)2=
(a-b)3=a3-3a2b+3ab2-b3
(a-b)(a2-2ab+b2)=
=a3 -2a2b+ab2-ba2+2ab2-b3=
a3-3a2b+3ab2-b3
Слайд 33Екі өрнектің кубтарының қосындысы
Теңбе-теңдік екі өрнектің кубтарының қосындысының формуласы деп
аталады .
(6)
a3+b3=
a3+b3=(a+b)(a2-ab+b2)
Екі өрнектің кубтарының қосындысы осы өрнектердің қосындысын олардың
айырмасының толымсыз квадратына көбейткенге тең. a3+ a2b- a2b
+ ab2- ab2
+ b3=
= a2(a+ b)-ab(a+b)+b2 (a+b)=
(a+b)(a3-ab+b3)
a2-2ab+b2 үшмүшесі айырманың толық квадраты деп аталады. Сондықтан a2-ab+b2 үшмүшесін айырманың толымсыз квадраты деп атайды.
Слайд 35Екі өрнектің кубтарының айырмасын көбейткіштерге жіктеу үшін:
Теңбе-теңдік екі өрнектің кубтарының
айырмасының формуласы деп атайды
(7)
a3-b3=
Екі өрнектің кубтарының айырмасы осы өрнектердің
айырмасын олардың қосындысының толымсыз квадратына көбейткенге тең.(a-b)(a2+ab+b2)
Сондықтан a 2 + ab + b 2 үшмүшесін айырманың толымсыз квадраты деп атайды.
Слайд 37(a+b)3 = a3+3a2b+3ab2+b3
(a-b)3 = a3 - 3a2b+3ab2 - b3
(4)
(6)
a3-b3 =
(a-b)(a2+ab+b2)
a3+b3 = (a+b)(a2–ab+b2)
(a+b)2 = a 2 + 2ab +
b 2 (a-b)2 = a2 - 2ab + b 2
a2-b2 = (a+b)(a-b)
(3)
(5)
(7)
(2)
(1)
Кысқаша көбейту формулалары
Слайд 38 Біз қысқаша көбейту формуласын дәлелдеудің екі жолын
қарастырдық.
Сіздер формуланы геометриялық жолмен де дәлелдеуге болатынын көрдіңіздер.
Ал енді
практикалық жұмысқа көшейік.Қазір осы формулалар есептер шығаруда қалай қолданылатындығын көрейік.
Менімен бірге орындаңыздар.
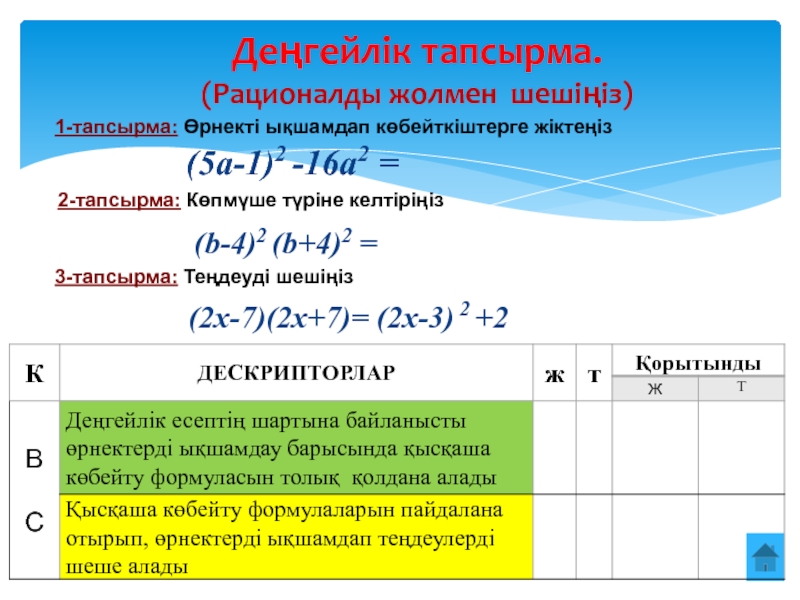
Слайд 41Деңгейлік тапсырма.
(Рационалды жолмен шешіңіз)
1-тапсырма: Өрнекті ықшамдап көбейткіштерге жіктеңіз
2-тапсырма: Көпмүше түріне
келтіріңіз
(5a-1)2 -16a2 =
(b-4)2 (b+4)2
= 3-тапсырма: Теңдеуді шешіңіз
(2x-7)(2x+7)= (2x-3) 2 +2
Слайд 42Жауаптары:
1-тапсырма: Өрнекті ықшамдап көбейткіштерге жіктеңіз
2-тапсырма: Көпмүше түріне келтіріңіз
(5a-1)2
-16a2 = (5a-1 -4a) (5a-1+4a)=(a-1)(9a-1)
(b-4)2 (b+4)2
= ((b-4) (b+4) ) 2 = (b2- 16)2 =b4-32b 2 +256 3-тапсырма: Теңдеуді шешіңіз
(2x-7)(2x+7)= (2x-3) 2 +2
4x 2 -49= 4x 2 -12x+9+2
12x= 49+11
12x= 60
x= 5
Слайд 43Өзіндік жұмыс.
1-нұсқа.
2 -нұсқа.
№1 Өрнекті ықшамдап мәнін табыңыз:
(5x+4)(25x2-20x+16)-64,
мұндағы х=2.
(2а-b)(4a2+2ab+b2)+b3,
мұндағы a = -2, b=1
№2 Көпмүшені стандарт түрге келтіріңіз:
(2x+1)2-(x-5)(x+5).
(3a-2)(3a+2)+(2a-3)2.
№3 Теңдеуді шешіңіз:
(x-4)(x+4)-6х=(х-2)2.
(2х+3)2-7х=(2х-1)(2х+1)
Слайд 44№1 (5x+4)(25x2-20x+16)-64=
=(125х3+64)-64=125х3.
Мұндағы х=2;
125х3=125.8=1000
№1 (2а-b)(4a2+2ab+b2)+b3=
=(8a3-b3)+b3=8a3 .
Мұндағы a=-2;
b=1; 8a3=8.(-8)=-64
№2 (2x+1)2-(x-5)(x+5)=
=(4х2+4х+1)-(х2-25)=
=4х2+4х+1-х2+25=3х2+4х+26.
№2 (3a-2)(3a+2)+(2a-3)2=
=(9а2-4)+(4а2-12а+9)=
= 9а2-4+4а2-12а+9=13а2-12а+5.
Өзіңді тексер.
1-нұсқа. 2 -нұсқа.
Слайд 45Кейбір математикалық фокустар
Қосындының квадраты және айрманың квадраты формуласымен ойда есептеуге
мүмкіндік беретін кейбір математикалық фокустар орындалады. Мысалы, 1,2,3,8,9 бен аяқталатын
сандарды ауызша квадраттауға болады.71² = (70 + 1)² = 70² + 2·70·1 + 1² = 4900 + 140 + 1 = 5041
23² = (20 + 3)² = 20² + 2·20·3 + 3² = 400 + 120 + 9 = 529
49² = (50 - 1)² = 50² - 2·50·1 + 1² = 2500 – 100 + 1 = 2401
Бірақ ең керемет фокус 5-пен аяқталатын сандарды квадратқа шығару үшін орындалады:
35²=1225, 3·4=12 cодан кейін 25-ті тіркеп жазу керек 1225
85² = 7225, 8·9 = 72 cодан кейін 25-ті тіркеп жазу керек 7225
115²=13225, 11·12=132 cодан кейін 25-ті тіркеп жазу керек 13225
Слайд 46Қосындының квадраты мен айырманың квадраты формуласын қолданып есептеңіз
1) 792;
2) 212;
3) 882;
4) 982.
Слайд 47Жауаптары
(80-1)2 =6400-160+1= 6241;
(20+1)2=400+40+1= 441;
(90-2)2=8100-360+4=7744;
(100-2)2=10000-400+4=9604.
Слайд 48Оқушылар сабақтан алған әсерлері бойынша + немесе – таңбасын қояды
1.
Мен ойлаймын сабақ…….. болды
қызық___________________іш пысарлық
2. Мен үйрендім
көп нәрсе________________аз
3. Мен ойлаймын
басқаларды ……… тыңдадыммұқият__________________мұқиятсыз
4. Мен дискуссияға ………. қатыстым
жиі_____________________аз
5. Сабақ нәтижелеріне менің……
көңілім толады___________көңілім толмайды
«Таңдау»
Слайд 49Қолданылған әдебиеттер
1. Шыныбеков Ә.Н. Алгебра 7 сынып, Жалпы білім
беретін мектептің 7-сыныбына арналған оқулық. 4-басылымы. «Атамұра», 2012ж. 81-бет
2. Мордкович
Александр Григорьевич Алгебра, 7 класс, в двух частях, Часть 1 Учебник., 2010.- 113 стр. 3. А.Г Мордкович , Л.А. Александрова, Т.Н.Мишустина, Е.Е. Тульчинская Алгебра, 7 класс, в двух частях, Часть 1 Задачник для учащихся общеоброзовательных учреждений, 2010.- 126 стр.
4. М.Горднер Математические досуги, Москва, Мир 2000г
5. Зубарева И.И., Лепешонкова И.П., Мильштейн М.С. Математика. 6 сынып. Жалпы білім беретін мекемелер оқушыларына арналған жеке жұмыстар / 4-басылым. - М.: МНЕМОЗИНА. 2010.- 136 с.
6. Гамбарин В.Г., Зубарева И.И.математика бойынша есеп пен жаттығулар жинағы. 6 сынып: Жалпы білім беретін мекемелер оқушыларына арналған оқулық / - М.: МНЕМОЗИНА. 2009.- 95 с.:ил.
7. Кукин Г.П. Воеводина К.К. Комбинаторика для начинающих, Омск 1993г.