Электричество и магнетизм
Семинар № 1
Тема: «Расчёт напряжённости электрического поля»
План семинара
1.
Применение принципа суперпозиции. Решить задачи: 6.1; 6.3; 6.4.
2. Применение теоремы Гаусса.
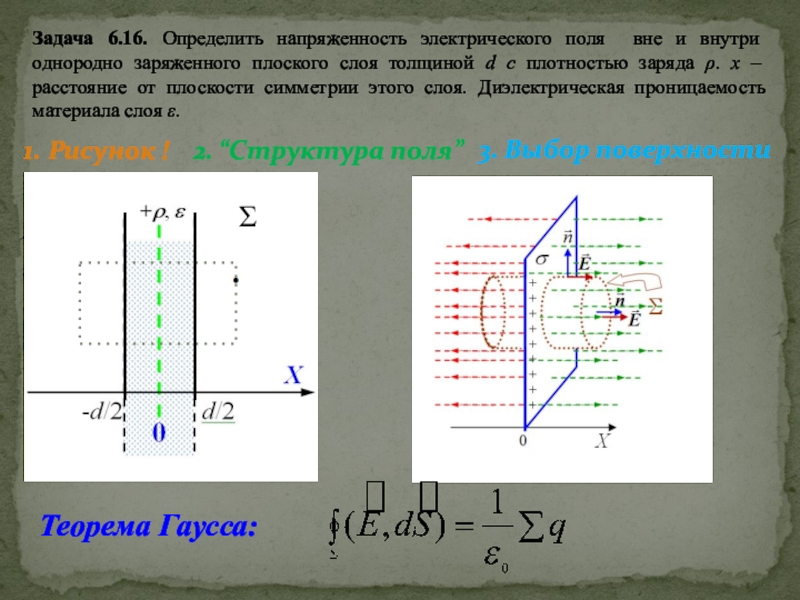
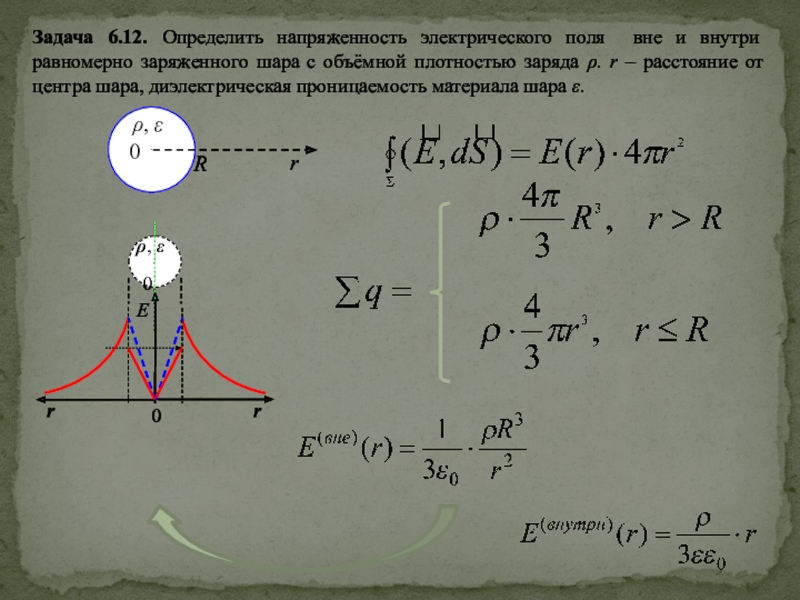
Решить задачи: 6.16; резерв: 6.12.
На дом: 6.2; 6.4 (доделать); 6.6; 6.10; 6.11; 6.12;
факультативно: посмотреть разобранную задачу 6.5.
Принцип суперпозиции полей