Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
Содержание
- 1. СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- 2. Средства обеспечения подсистем АСТППКОМПОНЕНТЫСРЕДСТВА ОБЕСПЕЧЕНИЯПОДСИСТЕМЫСистемы автоматизированного проектированияФункциональные (объектно-ориентированные)Инвариантные (объектно-независимые)МатематическоеЛингвистическоеПрограммноеТехническоеМетодическоеОрганизационноеИнформационное
- 3. Средства обеспечения систем автоматизированного проектирования Системы
- 4. Основные принципы построения и применения автоматизированных систем
- 5. Математическое обеспечение систем автоматизированного проектирования
- 6. Возможности математического моделирования Математическое моделирование
- 7. Возможности математического моделирования Математическая модель
- 8. Требования к математическим моделям К
- 9. Взаимосвязь требований к математическим моделям
- 10. Предположения по построению элементов математических моделей параллельной
- 11. Классификация методов моделирования Моделирование по
- 12. Взаимосвязь пространств, слоев и методов моделирования ЖЦИ Материальный слойИнформационный слой
- 13. Классификация кибернетических (математических) моделейКибернетические(математические)моделиАналитическиеДинамическиеНепрерывныеИмитационныеНединамические (статистические)ДискретныеМодели массового обслуживания и надежностиИгровые моделиМодели распознавания образовГрафовые моделиЛогико-алгебраичес-кие модели
- 14. Математический аппарат для построения кибернетических моделей
- 15. Схема классификации моделей и методов распознавания образовОбучение
- 16. Применение математических моделей Практическим применением
- 17. Этапы работ для выполнения математического моделирования
- 18. Этапы работ для выполнения математического моделирования
- 19. Скачать презентанцию
Средства обеспечения подсистем АСТППКОМПОНЕНТЫСРЕДСТВА ОБЕСПЕЧЕНИЯПОДСИСТЕМЫСистемы автоматизированного проектированияФункциональные (объектно-ориентированные)Инвариантные (объектно-независимые)МатематическоеЛингвистическоеПрограммноеТехническоеМетодическоеОрганизационноеИнформационное
Слайды и текст этой презентации
Слайд 1СИСТЕМЫ
АВТОМАТИЗИРОВАННОГО
ПРОЕКТИРОВАНИЯ
Раздел курса лекций по дисциплине
«Промышленные технологии и инновации»
Занятие 3
Российский
государственный университет
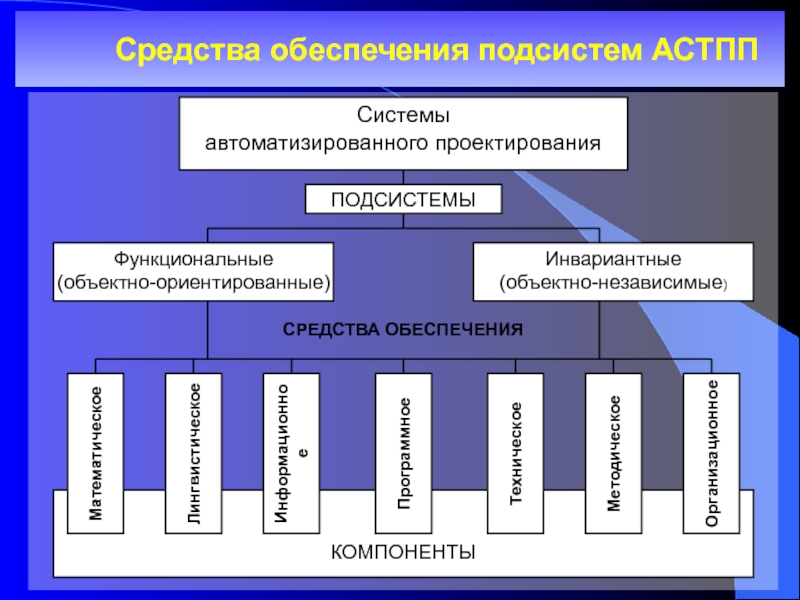
Слайд 2 Средства обеспечения подсистем АСТПП
КОМПОНЕНТЫ
СРЕДСТВА ОБЕСПЕЧЕНИЯ
ПОДСИСТЕМЫ
Системы
автоматизированного проектирования
Функциональные
(объектно-ориентированные)
Инвариантные
(объектно-независимые)
Математическое
Лингвистическое
Программное
Техническое
Методическое
Организационное
Информационное
Слайд 3Средства обеспечения
систем автоматизированного проектирования
Системы и подсистемы включают следующие
виды обеспечения:
математическое — математические модели, методы и алгоритмы автоматизированного проектирования;
лингвистическое
— совокупность языков, используемых в САПР для представления информации об объектах, процессах и средствах проектирования;информационное — документы, содержащие описание изделий и их элементов,
а также файлы и блоки данных на машинных носителях с записями документов;
программное — совокупность программ, представленных в заданной форме, вместе с необходимой программной документацией;
техническое — совокупность аппаратных средств, включающих устройства вычислительной и организационной техники, средства передачи данных, измерительные и другие устройства, используемые в САПР;
методическое — документы, в которых отражены состав, правила выбора
и эксплуатации средств автоматизированного проектирования;
организационное — положения, инструкции, приказы, штатные расписания, квалификационные требования и другие документы, регламентирующие организационную структуру проектной организации.
Слайд 4Основные принципы построения и применения
автоматизированных систем проектирования
Основными
принципами формирования взаимосвязанной совокупности методов и средств автоматизации проектирования, обеспечивающими
требуемый уровень конкурентоспособности проектных решений, являются: принцип системного единства, принцип комплексности и принцип информационного единства.Принцип системного единства состоит в том, что на всех стадиях и этапах жизненного цикла изделий и систем их проектирования, производства и эксплуатации функционирование и развитие систем информационной поддержки обеспечивается в едином пространстве взаимосвязями и взаимодействием автоматизированных систем.
Принцип комплексности заключается в том, что обеспечивается взаимосвязь всех видов проектирования структурных элементов и всего объекта в целом для всех стадий и этапов жизненного цикла сложных технических объектов.
Принцип информационного единства состоит в том, что в автоматизированных системах, обеспечивающих проектирование, в их функциональных и инвариантных подсистемах и средствах обеспечения используются единые: терминология, способы представления информации и проблемно-ориентированные языки проектирования.
Методологической основой обеспечения принципов системного единства, комплексности и информационного единства является формализованный подход к определению пространства проектирования и его структуризации, а также применение функционально-стоимостного анализа для комплексной оценки проектных решений.
Слайд 5Математическое обеспечение
систем автоматизированного проектирования
Для эффективного решения задач
параллельного
проектирования в прикладной области знаний систем автоматизированного проектирования
и информационной поддержки
процессовсоздания и эксплуатации сложных технических объектов
необходимы:
теория автоматизации проектирования,
специфическая методология и аппарат исследования,
а также языки представления
теории и объектов моделирования.
Слайд 6Возможности
математического моделирования
Математическое моделирование дает возможность
в сжатые сроки
и без значительных затрат ресурсов
исследовать и предсказывать свойства и
поведение объектовв заданных условиях.
Переход от реального физического объекта
к его математическому описанию
позволяет, создавая математическую модель,
использовать аппарат современной математики
и инструментарий вычислительной техники.
Математическая модель – приближенное описание определенных классов объектов и явлений реального мира, выраженное в терминах математической символики.
Слайд 7Возможности
математического моделирования
Математическая модель – приближенное описание определенных
классов объектов и явлений реального мира, выраженное в терминах математической
символики.Математическая символика является
наиболее удобным средством для описания, в первую очередь,
количественных свойств явлений и объектов,
а также их структурных свойств и логики функционирования.
Перед выполнением исследований
методами математического моделирования
необходимо установить
адекватность моделей реальным объектам
и проверить математические модели
на логическую непротиворечивость,
а также оценить возможную точность получаемых результатов.
Слайд 8Требования
к математическим моделям
К математическим моделям предъявляются требования:
универсальности,
адекватности, точности и экономичности.
Степень универсальности ММ характеризует
полноту отображения в модели элементов и свойств реального объекта.Как правило, ММ отражает лишь небольшую часть свойств объекта. Большинство моделей функционального проектирования отображают протекающие в объекте физические или информационные процессы, при этом не требуется таких свойств, как геометрическая форма составляющих элементов.
Адекватность ММ - способность отображать заданные свойства объекта с погрешностью не выше заданной.
Адекватность модели может иметь место в ограниченной области изменений внешних воздействий. Эта область называется областью адекватности математической модели.
Слайд 9Взаимосвязь требований
к математическим моделям
Требования высокой точности и
степени универсальности,
а также широкой области адекватности, с одной стороны,
и высокой
экономичности, с другой стороны, противоречивы.Наилучшее удовлетворение этих противоречивых требований зависит от особенностей решаемых задач, иерархического уровня и аспектов моделирования.
Все это приводит к применению широкого спектра математических (кибернетических) моделей.
Экономичность ММ - характеризуется затратами
вычислительных ресурсов на ее реализацию.
Слайд 10Предположения по построению элементов
математических моделей параллельной среды
Для построения модели элемента системы
параллельной
технологической средыпринимаются следующие предположения:
Моделирование материальных и энергетических преобразований происходит только в элементах системы
(предположение сосредоточенного преобразования).
2. Математическая модель элемента описывает поведение элемента как целого независимо от способа соединения с другими элементами системы (предположение независимости).
3. Моделью элемента системы проектирования на концептуальном уровне является граф вида “дерево”, информационные потоки в котором соответствуют дугам (предположение иерархичности).
4. Моделью системы проектирования в целом на концептуальном уровне является граф общего вида, объединяющий элементы системы, а процесс передачи информации имеет итерационный характер (предположение связности).
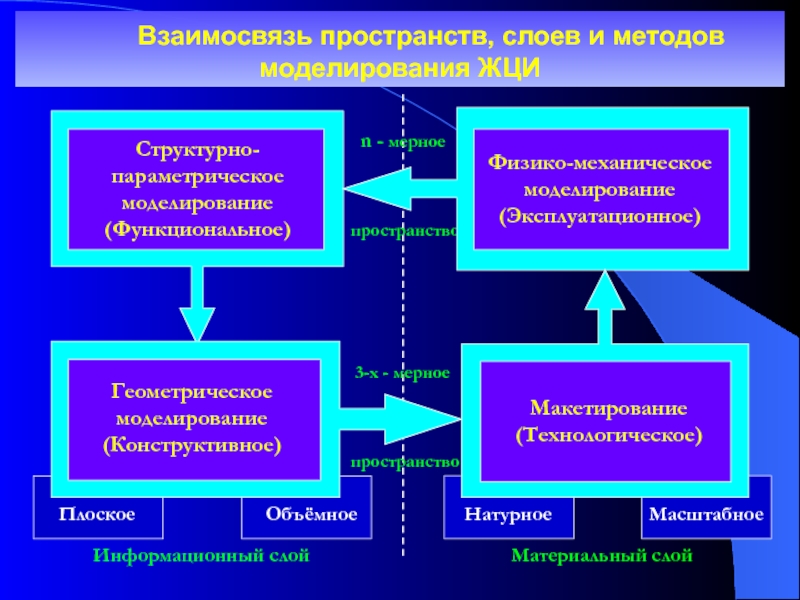
Слайд 11Классификация
методов моделирования
Моделирование по назначению подразделяется на: функциональное,
конструктивное,
технологическое, эксплуатационное.
Моделирование по видам делится на:
структурно-параметрическое, геометрическое,
натурное
(технологическое), физико-механическое.Пространства моделирования подразделяются на:
n-мерное; трехмерное (геометрическое),
где двухмерное - частный упрощенный случай.
Выделяются информационный и материальный
слои моделирования.
Слайд 12 Взаимосвязь пространств, слоев и методов
моделирования ЖЦИ
Материальный слой
Информационный слой
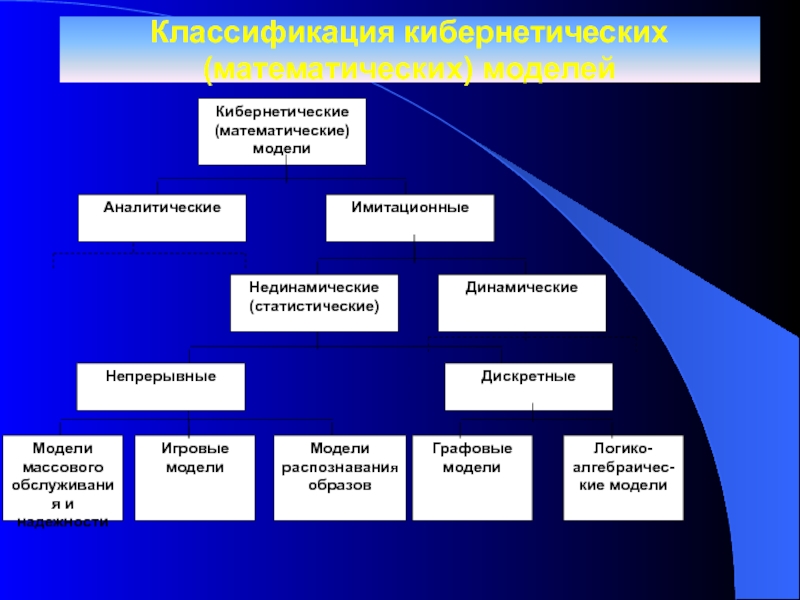
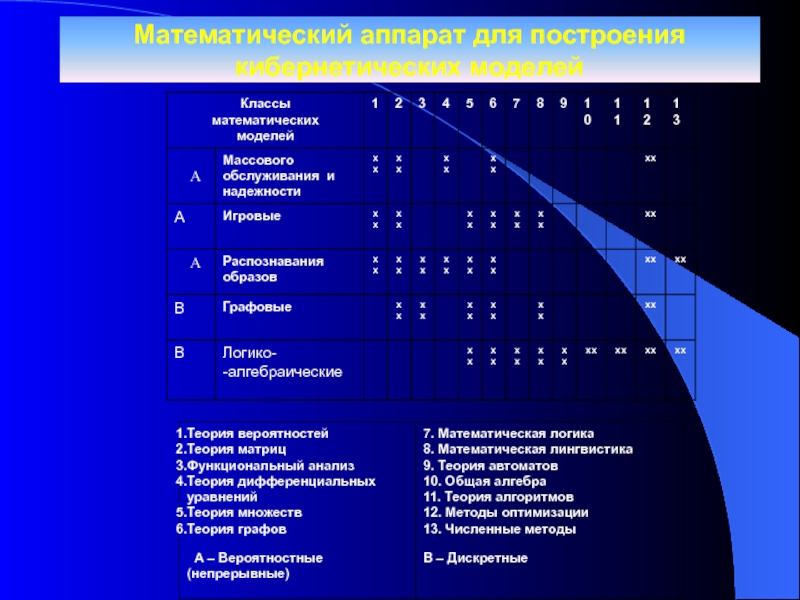
Слайд 13Классификация кибернетических (математических) моделей
Кибернетические
(математические)
модели
Аналитические
Динамические
Непрерывные
Имитационные
Нединамические
(статистические)
Дискретные
Модели массового обслуживания и надежности
Игровые модели
Модели
распознавания образов
Графовые модели
Логико-алгебраичес-кие модели
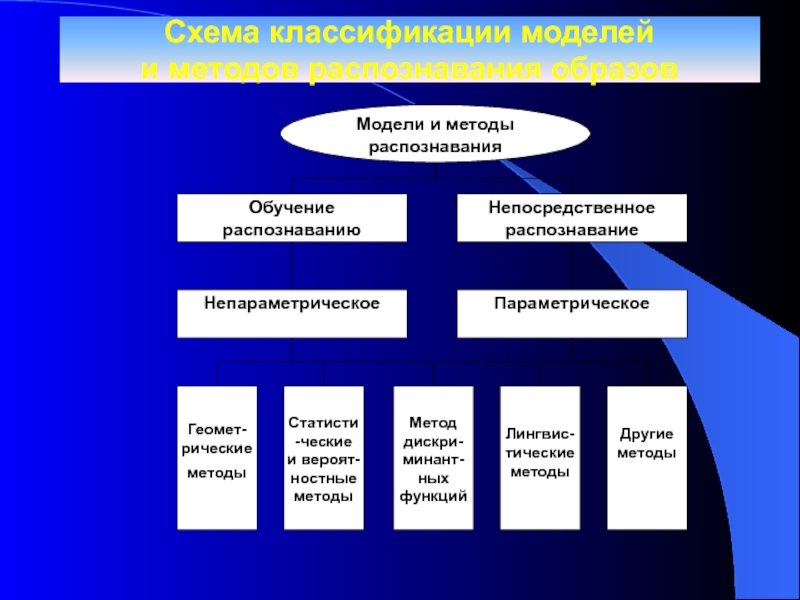
Слайд 15Схема классификации моделей
и методов распознавания образов
Обучение распознаванию
Непосредственное распознавание
Непараметрическое
Параметрическое
Геомет-рические
методы
Статисти-ческие
и
вероят-ностные
методы
Метод дискри-минант-ных функций
Лингвис-тические методы
Другие
методы
Модели и методы распознавания
Слайд 16Применение
математических моделей
Практическим применением математических (кибернетических) моделей занимаются
совместно
со специалистами различных предметных областей специалисты в области прикладной
математики(раздел прикладной математики получил название «Исследование операций").
Для реализации кибернетических моделей необходимо выполнить определенные этапы работ.
Слайд 17Этапы работ для выполнения
математического моделирования
Постановка задач, включающая
выбор метода
моделирования, класса математической модели,
состава моделируемых объектов, их параметров
Определение критериев для выбораобласти рациональных решений
или установление критерия
для выбора оптимального решения
Разработка алгоритма, определение состава
и последовательности проектных процедур
для реализации процесса моделирования
на вычислительной технике
Слайд 18Этапы работ для выполнения
математического моделирования
Создание программного обеспечения
реализующего
алгоритмы проектирования
в соответствии с математической моделью
и принятыми способами ее представления
Выбор технического обеспечениянеобходимого и достаточного
для эффективной эксплуатации программного обеспечения
Подготовка исходных данных
Выполнение моделирования
(аналитического или имитационного)
Анализ получаемых результатов.