Системы счисления

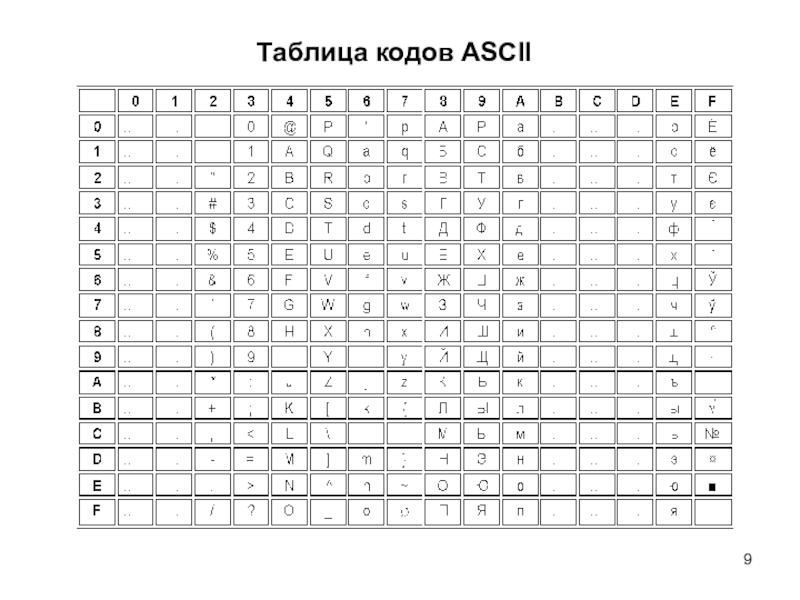
набора символов.
Система счисления — набор правил представления чисел с помощью

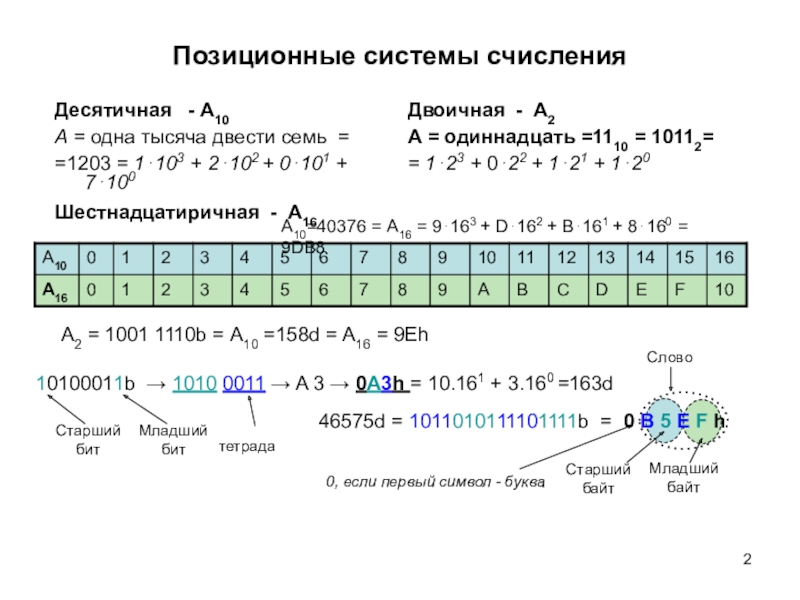
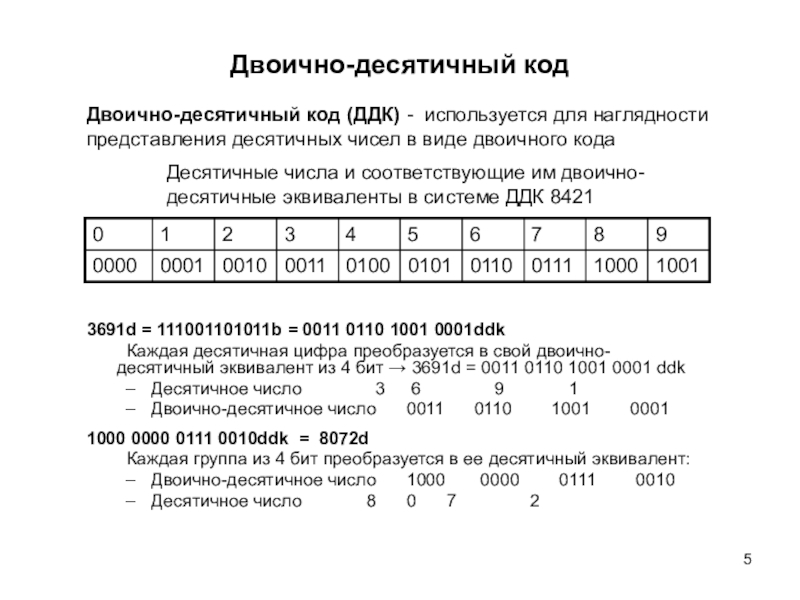
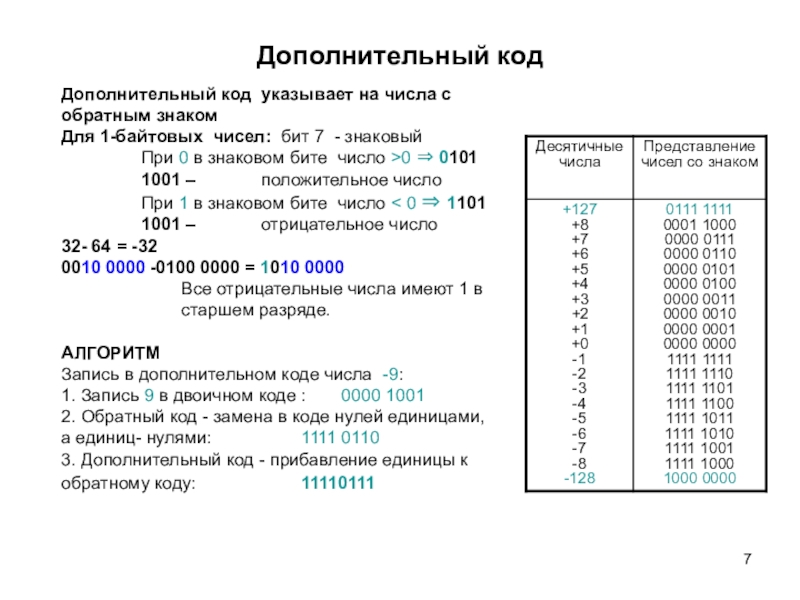
письменных знаков.
Системы счисления - позиционные, непозиционные и смешанные.
В позиционных системах счисления значение символа (цифры) в записи числа зависит от того места (разряда), где он расположен.
Целое число Х в b - ричной позиционной системе
счисления представляется в виде
линейной комбинации степеней числа b:
b - основание системы счисления, целое число, b > 1,
ak — целые числа - цифры , причем 0  ак (b-1),
bk - весовой коэффициент разряда.
Старшинство разрядов - показатель k
Число Х записывают в виде последовательности его b-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:
Х = an-1an-2…аa0

семь =
=1203 = 1103 + 2102 + 0101 +

7100
Шестнадцатиричная - А16

Двоичная - А2
А = одиннадцать =1110 = 10112=
= 123 + 022 + 121 + 120

А2 = 1001 1110b = А10 =158d = А16 = 9Eh

10100011b  1010 0011  A 3  0A3h = 10.161 + 3.160 =163d

Старший бит

Младший бит

46575d = 1011010111101111b = 0 B 5 E F h

Старший байт

Младший байт

Слово

А10=40376 = А16 = 9163 + D162 + B161 + 8160 = 9DB8

0, если первый символ - буква

тетрада

бит двоичного числа
77d : 2 = 38d +1
38d : 2

= 19d +0
19d : 2 = 9d +1
9d : 2 = 4d + 1
4d : 2 = 2d + 0
2d : 2 = 1d + 0
1d : 2 = 0d + 1  Старший бит двоичного числа
Результат:
155d = 10011011b

5d  5h – младший символ шестнадцатеричного числа.
987d : 16d

= 61d + 11d  Вh
61d : 16d = 3d + 13d  Dh
3d : 16d = 0 d +3d  3h - символ (цифра) в старшем разряде шестнадцатеричного числа
15797d = 3DB5h.

цифра преобразуется в свой двоично-десятичный эквивалент из 4 бит 

3691d = 0011 0110 1001 0001 ddk
Десятичное число 3 6 9 1
Двоично-десятичное число 0011 0110 1001 0001
1000 0000 0111 0010ddk = 8072d
Каждая группа из 4 бит преобразуется в ее десятичный эквивалент:
Двоично-десятичное число 1000 0000 0111 0010
Десятичное число 8 0 7 2

Двоично-десятичный код (ДДК) - используется для наглядности представления десятичных чисел в виде двоичного кода
Десятичные числа и соответствующие им двоично-десятичные эквиваленты в системе ДДК 8421

переноса
Вычитание
0-0=0
1-0=1
1-1=0
0 -1 =1
Пример:
01010101
00111001
00011100
Бит заёма
Умножение
0х0=0
1х0=0
0х1=0
1х1=1
1101b x 101b =13d x

5d=65d =1000001b

Пример:
1101
X 101
1101
0000
1101
1000001

1-байтовых чисел: бит 7 - знаковый
При 0 в знаковом бите

число >0  0101 1001 – положительное число
При 1 в знаковом бите число < 0  1101 1001 – отрицательное число
32- 64 = -32
0010 0000 -0100 0000 = 1010 0000
Все отрицательные числа имеют 1 в старшем разряде.

АЛГОРИТМ
Запись в дополнительном коде числа -9:
1. Запись 9 в двоичном коде : 0000 1001
2. Обратный код - замена в коде нулей единицами, а единиц- нулями: 1111 0110
3. Дополнительный код - прибавление единицы к обратному коду: 11110111

представление символьной информации в операционных системах и текстовых файлах.
Структура

кода представляется в виде таблицы, которая содержит 16 столбцов и 16 строк
Каждая строка и столбец пронумерованы в шестнадцатеричной системе счисления цифрами от 0 до F.
Шестнадцатеричное представление ASCII-кода складывается из номера столбца и номера строки, в которых располагается символ.
6D – означает, что символ находится в на пересечении
6-го столбца и строки D
В двоичной системе код представляется 8 разрядами код 6Dh  0110 1101d
Столбцы с номерами от 0 до 7 - стандарт кода, его неизменяемая часть
Столбцы с номерами 0 и 1 и код 127d - управляющие символы, в том числе внешними устройствами (принтером)
Столбцы с номерами от 2 до 7 - знаки препинания, знаки арифметических действий, служебные символы, заглавные и строчные буквы латинского алфавита
Столбцы с номерами от 8 до F - расширение кода - символы псевдографики, буквы национальных алфавитов и другие символы.

б) 0101; в) 1000; г) 1011; д) 1111; е) 0111.
2.

Преобразовать в десятичный код следующие двоичные числа:
а) 10000000; б)00010000; в) 00110011; г) 01100100; д) 00011111;
3. Преобразовать в двоичный код следующие десятичные числа:
а) 23; б) 39; в) 55; г) 48.
4. Записать следующие шестнадцатеричные числа в двоичной форме:
а) С; б) 6; в) F; г) Е; д) 1А; е) 3D; ж) АО; з) 8В; и) 45; к) D7.
5. Преобразовать следующие двоичные числа в шестнадцатеричный код:
а) 1001; б) 1100; в) 1111; г) 10000000; д) 01111110; е) 0010101;
6. Преобразовать шестнадцатеричные числа в десятичный код:
а) 7Е; б) DB; в) 12А3; г) 34CF.
7. Записать следующие десятичные числа в ДДК:
а) 39; б) 65; в) 40; г) 17; д) 82;
8. Записать следующие двоично-десятичные числа в десятичном коде:
а) 1000 0000; б) 0000 0001; в) 1001 0010; г) 0111 0110; д) 0100 0011 ;
9) Записать следующие слова и выражения в кодировке ASCII
а) Ступа; б) Компьютер, в) 170-583 = -413; г) Star; д) FLAG; е)Decimal

б) 1101 в) 1011011

г) 0011 1111 + + + +
0101 0101 0000 1111 0001 1111.

Выполнить следующие вычитания двоичных чисел: а) 1110 6)1010 в). 100110 г) 0111 1000
- - - -
1000 0101 01 1010 0110 1111.

Выполнить следующие умножения двоичных чисел:
а) 1001 б) 1101 в) 1111 г) 1110
х х х х
11 1001 101 1110.