Сложение колебаний

Содержание

1. Сложение колебаний
2. Сложение однонаправленных колебаний. Пусть материальная точка участвует одновременно
3. Для колебаний с одинаковыми частотами имеем: Сложение
4. Метод векторных диаграмм.Идея метода основана на двух
5. Метод векторных диаграмм.,Проекции вектора на оси: Если
6. Метод векторных диаграмм.Видно, что каждая из величин
7. Метод векторных диаграмм.Пусть теперь в плоскости XY
8. Метод векторных диаграмм.Углы 01 и 02 можно
9. Метод векторных диаграмм.Сумма проекций векторов на ось
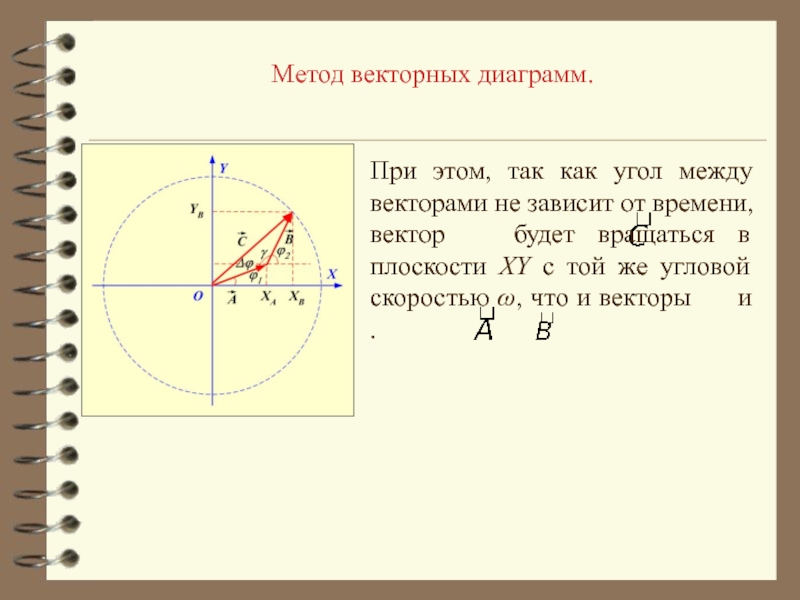
10. Метод векторных диаграмм.При этом, так как угол
11. Метод векторных диаграмм.Алгоритм применения графического способа сложения
12. Метод векторных диаграмм.Модуль суммарного вектора можно определить с помощью теоремы косинусов cos( - ) = -cos()
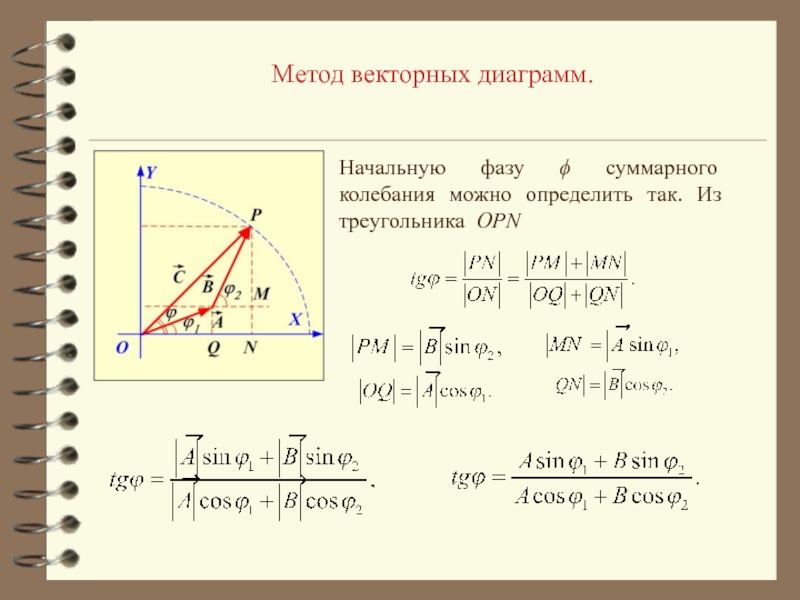
13. Метод векторных диаграмм.Начальную фазу  суммарного колебания можно определить так. Из треугольника OPN
14. Метод векторных диаграмм.
15. Метод векторных диаграмм.
16. Метод векторных диаграмм.
17. Метод векторных диаграмм.
18. Скачать презентанцию

Сложение однонаправленных колебаний. Пусть материальная точка участвует одновременно в двух гармонических колебаниях, причем движение совершается вдоль одного направления. Тогда её смещение из положения равновесия складывается из двух смещений: Если частоты колебаний различны,

Слайды и текст этой презентации

Слайд 1Сложение колебаний
Сложение однонаправленных колебаний, происходящих с одинаковой частотой.
Метод векторных

диаграмм.

Слайд 2Сложение однонаправленных колебаний.
Пусть материальная точка участвует одновременно в двух гармонических

колебаниях, причем движение совершается вдоль одного направления. Тогда её смещение

из положения равновесия складывается из двух смещений:

Если частоты колебаний различны, то картина движения точки будет достаточно сложной. Если же частоты одинаковы, результирующее движение также будет гармоническим колебанием.

Электромагнитные колебания (например, колебания силы тока в цепях переменного тока) также подчиняются гармоническому закону. Если в цепи происходят одновременно два гармонических колебания, то результирующий ток можно записать так:

Сложение однонаправленных колебаний. Пусть материальная точка участвует одновременно в двух гармонических колебаниях, причем движение совершается вдоль одного направления.

Слайд 3Для колебаний с одинаковыми частотами имеем:
Сложение однонаправленных колебаний.
Уравнения, описывающие

как механические, так и электромагнитные колебания, одинаковы, следовательно метод сложения

колебаний будет одним и тем же, а результаты сходными.

Для колебаний с одинаковыми частотами имеем: Сложение однонаправленных колебаний.Уравнения, описывающие как механические, так и электромагнитные колебания, одинаковы,

Слайд 4Метод векторных диаграмм.
Идея метода основана на двух простых положениях.
Проекция

вектора с модулем R на любую из координатных осей, вращающегося

с постоянной угловой скоростью, совершает гармонические колебания.
При сложении двух векторов проекция суммарного вектора равна сумме проекций складываемых векторов.

Метод векторных диаграмм.Идея метода основана на двух простых положениях. Проекция вектора с модулем R на любую из

Слайд 5Метод векторных диаграмм.
,
Проекции вектора на оси:
Если вектор вращается с

постоянной угловой скоростью ω, то  = t + 0.
С

течением времени величины проекций вращающегося вектора изменяются так:

Метод векторных диаграмм.,Проекции вектора на оси: Если вектор вращается с постоянной угловой скоростью ω, то  =

Слайд 6Метод векторных диаграмм.
Видно, что каждая из величин проекций вектора изменяется

по гармоническому закону, так же, как и любые величины, совершающие

гармонические колебания. В дальнейшем будем рассматривать только проекции векторов на ось OX.

Метод векторных диаграмм.Видно, что каждая из величин проекций вектора изменяется по гармоническому закону, так же, как и

Слайд 7Метод векторных диаграмм.
Пусть теперь в плоскости XY вокруг оси, проходящей

через начало координат вращаются два вектора.
Если векторы вращаются с

одинаковой угловой скоростью , то

При этом угол между векторами

Метод векторных диаграмм.Пусть теперь в плоскости XY вокруг оси, проходящей через начало координат вращаются два вектора. Если

Слайд 8Метод векторных диаграмм.
Углы 01 и 02 можно отождествить с начальными

фазами гармонических колебаний, модули векторов – с амплитудами гармонических колебаний,

а величину угловой скорости вращения векторов – с циклической частотой гармонических колебаний. В таком случае величина 0 является разностью фаз двух гармонических колебаний.

Метод векторных диаграмм.Углы 01 и 02 можно отождествить с начальными фазами гармонических колебаний, модули векторов – с

Слайд 9Метод векторных диаграмм.
Сумма проекций векторов на ось OX
Таким образом, сумма

проекций векторов равна сумме двух гармонических функций с одинаковой циклической

частотой и разными фазами.

Геометрически сумма проекций двух векторов на ось OX равна проекции на ось OX вектора

Метод векторных диаграмм.Сумма проекций векторов на ось OXТаким образом, сумма проекций векторов равна сумме двух гармонических функций

Слайд 10Метод векторных диаграмм.
При этом, так как угол между векторами не

зависит от времени, вектор будет вращаться в плоскости XY

с той же угловой скоростью , что и векторы и .

Метод векторных диаграмм.При этом, так как угол между векторами не зависит от времени, вектор будет вращаться

Слайд 11Метод векторных диаграмм.
Алгоритм применения графического способа сложения гармонических колебаний с

одинаковой частотой, называемого методом векторных диаграмм.
1. Выбрать оси координат и

построить векторные диаграммы складываемых колебаний. Длина вектора должна быть равна амплитуде колебаний, а угол наклона к оси – начальной фазе колебаний.

2. Построить, пользуясь правилом параллелограмма, вектор, равный сумме двух складываемых векторов.

3. Длина (модуль) суммарного вектора равна амплитуде суммарного колебания, угол наклона суммарного вектора к оси – его начальной фазе.

Метод векторных диаграмм.Алгоритм применения графического способа сложения гармонических колебаний с одинаковой частотой, называемого методом векторных диаграмм.1. Выбрать

Слайд 12Метод векторных диаграмм.
Модуль суммарного вектора можно определить с помощью теоремы

косинусов
cos( - ) = -cos()

Слайд 13Метод векторных диаграмм.
Начальную фазу  суммарного колебания можно определить так.

Из треугольника OPN

Слайд 14Метод векторных диаграмм.

Слайд 15Метод векторных диаграмм.

Слайд 16Метод векторных диаграмм.

Слайд 17Метод векторных диаграмм.

Скачать презентацию

Разделы презентаций

Сложение колебаний

Содержание

Слайды и текст этой презентации

Слайд 1Сложение колебаний
Сложение однонаправленных колебаний, происходящих с одинаковой частотой.
Метод векторных

диаграмм.

Слайд 2Сложение однонаправленных колебаний.
Пусть материальная точка участвует одновременно в двух гармонических

колебаниях, причем движение совершается вдоль одного направления. Тогда её смещение

Слайд 3Для колебаний с одинаковыми частотами имеем:
Сложение однонаправленных колебаний.
Уравнения, описывающие

как механические, так и электромагнитные колебания, одинаковы, следовательно метод сложения

Слайд 4Метод векторных диаграмм.
Идея метода основана на двух простых положениях.
Проекция

вектора с модулем R на любую из координатных осей, вращающегося

Слайд 5Метод векторных диаграмм.
,
Проекции вектора на оси:
Если вектор вращается с

постоянной угловой скоростью ω, то  = t + 0.
С

Слайд 6Метод векторных диаграмм.
Видно, что каждая из величин проекций вектора изменяется

по гармоническому закону, так же, как и любые величины, совершающие

Слайд 7Метод векторных диаграмм.
Пусть теперь в плоскости XY вокруг оси, проходящей

через начало координат вращаются два вектора.
Если векторы вращаются с

Слайд 8Метод векторных диаграмм.
Углы 01 и 02 можно отождествить с начальными

фазами гармонических колебаний, модули векторов – с амплитудами гармонических колебаний,

Слайд 9Метод векторных диаграмм.
Сумма проекций векторов на ось OX
Таким образом, сумма

проекций векторов равна сумме двух гармонических функций с одинаковой циклической

Слайд 10Метод векторных диаграмм.
При этом, так как угол между векторами не

зависит от времени, вектор будет вращаться в плоскости XY

Слайд 11Метод векторных диаграмм.
Алгоритм применения графического способа сложения гармонических колебаний с

одинаковой частотой, называемого методом векторных диаграмм.
1. Выбрать оси координат и

Слайд 12Метод векторных диаграмм.
Модуль суммарного вектора можно определить с помощью теоремы

косинусов
cos( - ) = -cos()

Слайд 13Метод векторных диаграмм.
Начальную фазу  суммарного колебания можно определить так.

Из треугольника OPN

Слайд 14Метод векторных диаграмм.

Слайд 15Метод векторных диаграмм.

Слайд 16Метод векторных диаграмм.

Слайд 17Метод векторных диаграмм.

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Сложение колебаний

Содержание

Слайды и текст этой презентации

Слайд 1Сложение колебанийСложение однонаправленных колебаний, происходящих с одинаковой частотой. Метод векторных

диаграмм.

Слайд 2Сложение однонаправленных колебаний. Пусть материальная точка участвует одновременно в двух гармонических

колебаниях, причем движение совершается вдоль одного направления. Тогда её смещение

Слайд 3Для колебаний с одинаковыми частотами имеем: Сложение однонаправленных колебаний.Уравнения, описывающие

как механические, так и электромагнитные колебания, одинаковы, следовательно метод сложения

Слайд 4Метод векторных диаграмм.Идея метода основана на двух простых положениях. Проекция

вектора с модулем R на любую из координатных осей, вращающегося

Слайд 5Метод векторных диаграмм.,Проекции вектора на оси: Если вектор вращается с

постоянной угловой скоростью ω, то  = t + 0.С

Слайд 6Метод векторных диаграмм.Видно, что каждая из величин проекций вектора изменяется

по гармоническому закону, так же, как и любые величины, совершающие

Слайд 7Метод векторных диаграмм.Пусть теперь в плоскости XY вокруг оси, проходящей

через начало координат вращаются два вектора. Если векторы вращаются с

Слайд 8Метод векторных диаграмм.Углы 01 и 02 можно отождествить с начальными

фазами гармонических колебаний, модули векторов – с амплитудами гармонических колебаний,

Слайд 9Метод векторных диаграмм.Сумма проекций векторов на ось OXТаким образом, сумма

проекций векторов равна сумме двух гармонических функций с одинаковой циклической

Слайд 10Метод векторных диаграмм.При этом, так как угол между векторами не

зависит от времени, вектор будет вращаться в плоскости XY

Слайд 11Метод векторных диаграмм.Алгоритм применения графического способа сложения гармонических колебаний с

одинаковой частотой, называемого методом векторных диаграмм.1. Выбрать оси координат и

Слайд 12Метод векторных диаграмм.Модуль суммарного вектора можно определить с помощью теоремы

косинусов cos( - ) = -cos()

Слайд 13Метод векторных диаграмм.Начальную фазу  суммарного колебания можно определить так.

Из треугольника OPN

Слайд 14Метод векторных диаграмм.

Слайд 15Метод векторных диаграмм.

Слайд 16Метод векторных диаграмм.

Слайд 17Метод векторных диаграмм.

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Сложение колебаний
Сложение однонаправленных колебаний, происходящих с одинаковой частотой.
Метод векторных

Слайд 2Сложение однонаправленных колебаний.
Пусть материальная точка участвует одновременно в двух гармонических

Слайд 3Для колебаний с одинаковыми частотами имеем:
Сложение однонаправленных колебаний.
Уравнения, описывающие

Слайд 4Метод векторных диаграмм.
Идея метода основана на двух простых положениях.
Проекция

Слайд 5Метод векторных диаграмм.
,
Проекции вектора на оси:
Если вектор вращается с

постоянной угловой скоростью ω, то  = t + 0.
С

Слайд 6Метод векторных диаграмм.
Видно, что каждая из величин проекций вектора изменяется

Слайд 7Метод векторных диаграмм.
Пусть теперь в плоскости XY вокруг оси, проходящей

через начало координат вращаются два вектора.
Если векторы вращаются с

Слайд 8Метод векторных диаграмм.
Углы 01 и 02 можно отождествить с начальными

Слайд 9Метод векторных диаграмм.
Сумма проекций векторов на ось OX
Таким образом, сумма

Слайд 10Метод векторных диаграмм.
При этом, так как угол между векторами не

Слайд 11Метод векторных диаграмм.
Алгоритм применения графического способа сложения гармонических колебаний с

одинаковой частотой, называемого методом векторных диаграмм.
1. Выбрать оси координат и

Слайд 12Метод векторных диаграмм.
Модуль суммарного вектора можно определить с помощью теоремы

косинусов
cos( - ) = -cos()

Слайд 13Метод векторных диаграмм.
Начальную фазу  суммарного колебания можно определить так.