Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СЛУ (Системы линейных уравнений)
Содержание
- 1. СЛУ (Системы линейных уравнений)
- 2. 1. Общий вид, основные понятия, матричная формаСистема
- 3. Если , то СЛУ называется однородной.Если хотя бы
- 4. Совместная система называется определенной, если она имеет
- 5. Любую СЛУ можно представить в матричном виде:На
- 6. 2. Методы решения СЛУМетод последовательного исключения неизвестных
- 7. Метод последовательного исключения неизвестных (Метод Гаусса)Рассмотрим СЛУ:Данный метод применим к СЛУ любой размерности.
- 8. Алгоритм метода:1 уравнение умножаем на
- 9. 1 случай:В этом случае СЛУ имеет единственное
- 10. 2 случай:В этом случае СЛУ имеет бесконечно
- 11. 3 случай:В этом случае СЛУ несовместна (не
- 12. Метод Гаусса (метод исключения неизвестных)Две системы
- 13. Схема действий метода Гаусса: а) из всех
- 14. Исключение неизвестных обычно осуществляют элементарными преобразованиями строк
- 15. Неизвестные, коэффициенты при которых вошли в базисный
- 16. Если n – число неизвестных системы, r
- 17. Если ранг основной и расширенной матриц СЛУ
- 18. Решение СЛУ, в котором базисные неизвестные выражены
- 19. Общее решение системы линейных уравнений можно получить,
- 20. Фундаментальной системой частных решений системы n однородных
- 21. Фундаментальную систему частныхрешений (ФСЧР СОЛУ) получают обычно,
- 22. 4. Метод Гаусса
- 23. Метод Гаусса (1)
- 24. Метод Гаусса (2)Рассмотрим систему
- 25. Метод Гаусса (3)Рассмотрим системуС помощью элементарных преобразований приводим ее к равносильной системе ступенчатого вида:
- 26. Метод Гаусса (4)Возможен один из следующих случаев:1)
- 27. Теорема Кронекера-Капелли (1)Рассмотрим систему уравнений
- 28. Теорема Кронекера-Капелли (2)Рассмотрим систему уравненийОбозначим
- 29. Теорема Кронекера-Капелли (3)
- 30. Пример 7 (1)Методом Гаусса решить систему уравнений:
- 31. Пример 7 (2)Решение. Запишем расширенную матрицу:
- 32. Пример 7 (3)
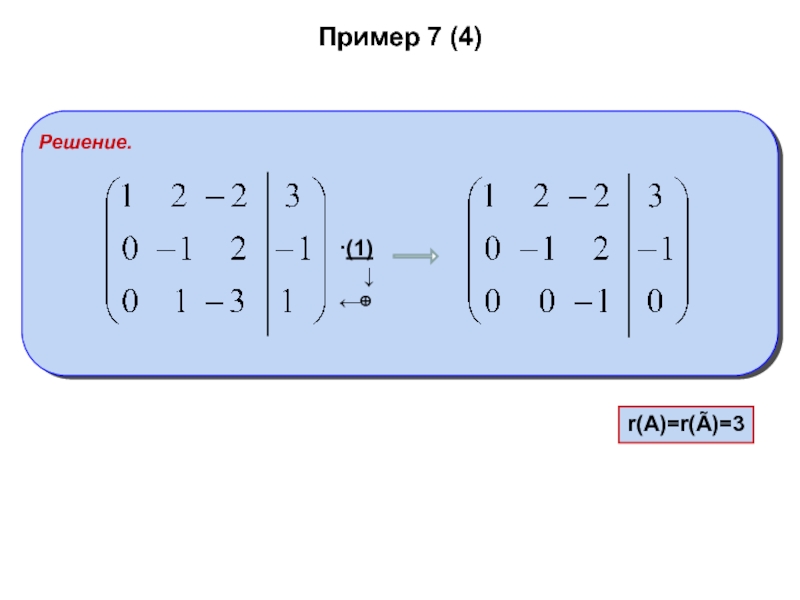
- 33. Пример 7 (4)
- 34. Пример 7 (4)r(A)=r(Ã)=3
- 35. Пример 7 (5)Решение.
- 36. Пример 7 (6)Решение.
- 37. Пример 7 (7)Решение. Найдем x1:
- 38. Пример 7 (8)Решение.x1=1, x2=1, x3=0 – единственное решение.
- 39. 2) Метод КрамераМетод основан на вычислении определителей, поэтому применим к СЛУ размерности nxn.Рассмотрим СЛУ:
- 40. Введем следующие обозначения:Теорема. Если
- 41. 3) Метод обратной матрицыМетод основан на нахождении
- 42. 3. Теорема Кронекера-КапеллиПомимо метода Гаусса, на вопрос
- 43. Слайд 43
- 44. Системы линейных уравнений (1)Системой m линейных уравнений
- 45. Пример 1
- 46. Пример 2
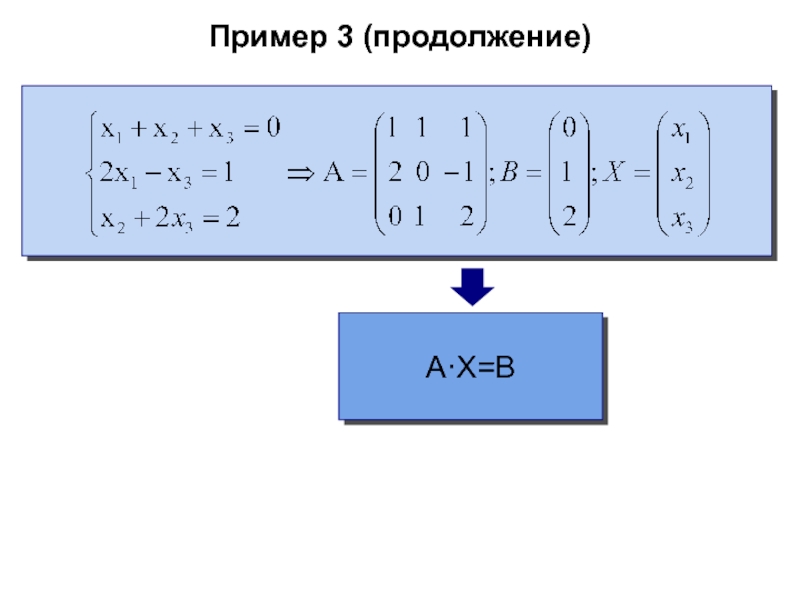
- 47. Пример 3
- 48. Системы линейных уравнений (2)
- 49. Матричный вид системыОбозначения:Матрица коэффициентов при неизвестныхСтолбец неизвестныхСтолбец свободных членов
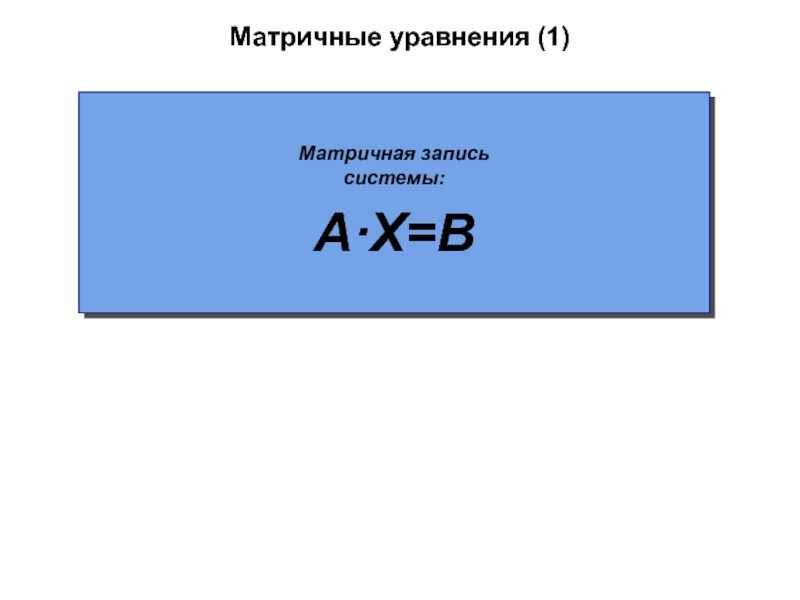
- 50. Матричные уравнения (1)Матричная запись системы:A·X=B
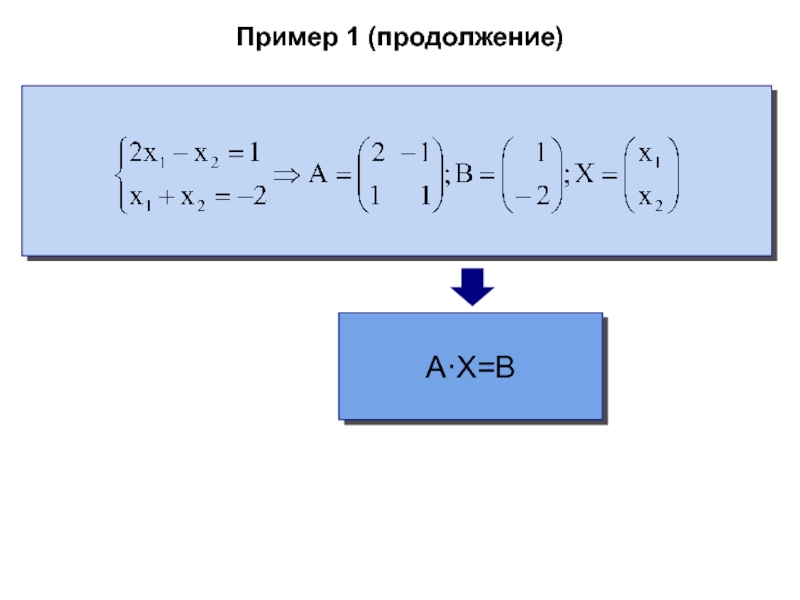
- 51. Пример 1 (продолжение)A·X=B
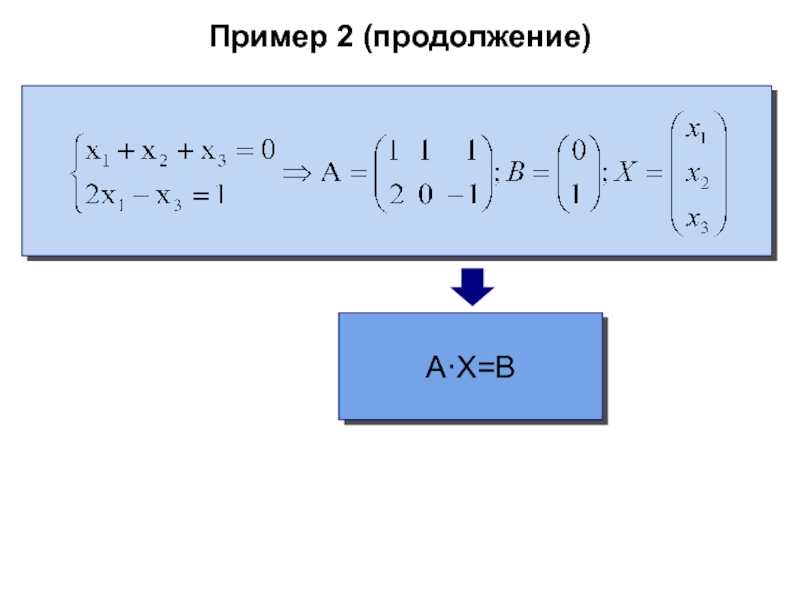
- 52. Пример 2 (продолжение)A·X=B
- 53. Пример 3 (продолжение)A·X=B
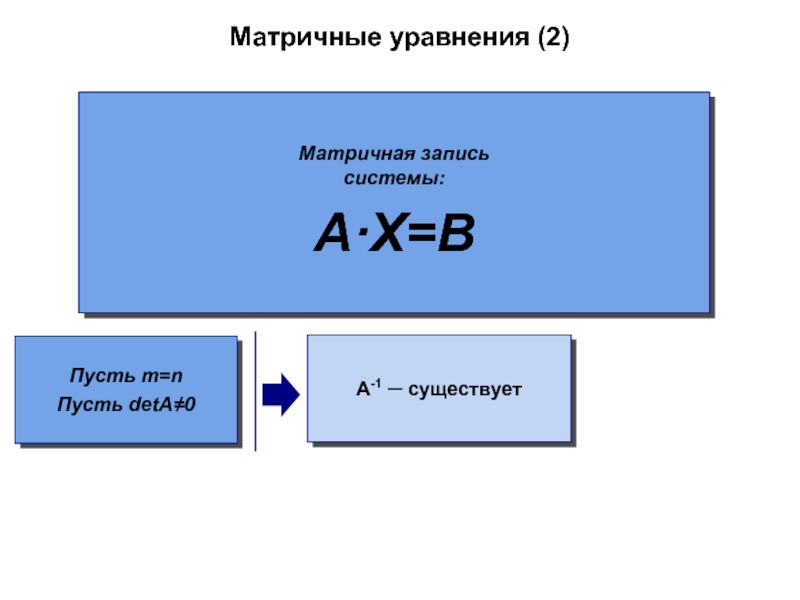
- 54. Матричные уравнения (2)Матричная запись системы:A·X=BA-1 ─ существуетПусть m=nПусть detA≠0
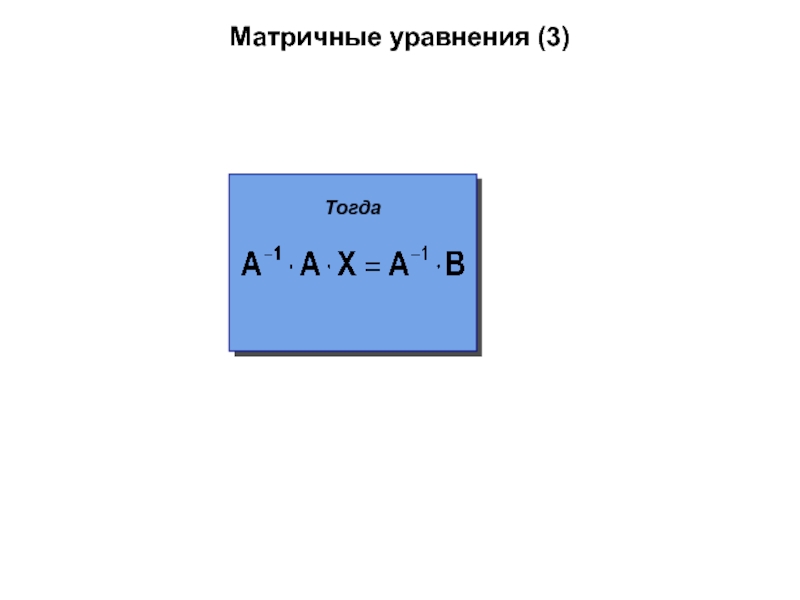
- 55. Матричные уравнения (3)Тогда
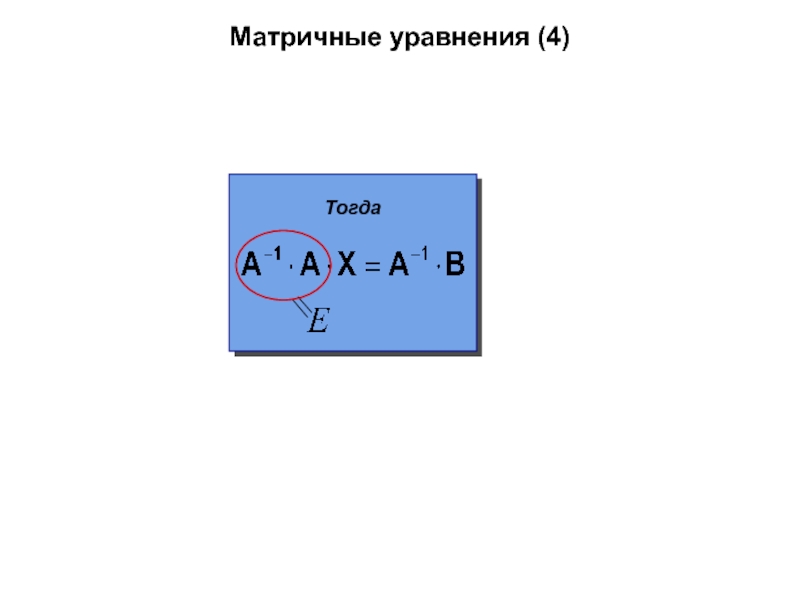
- 56. Матричные уравнения (4)Тогда
- 57. Матричные уравнения (5)Тогда
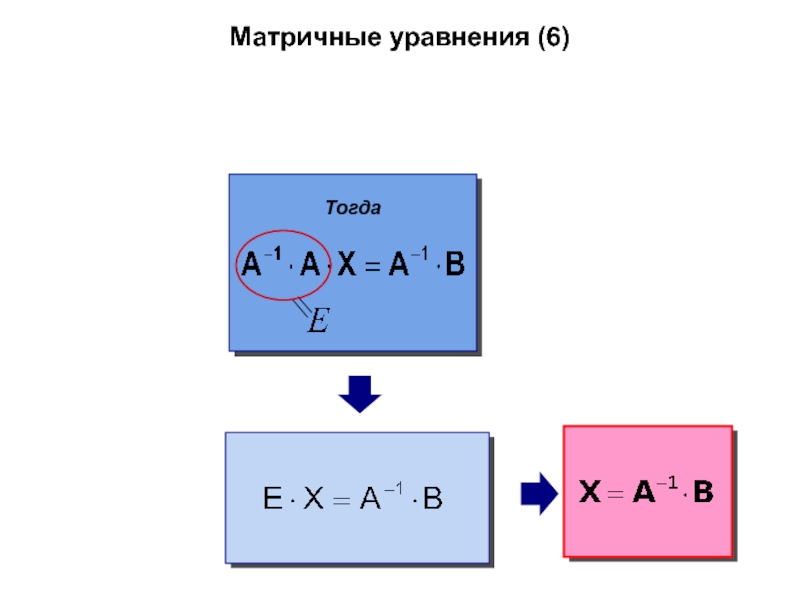
- 58. Матричные уравнения (6)Тогда
- 59. Пример 4 (1)Решите систему уравнений:
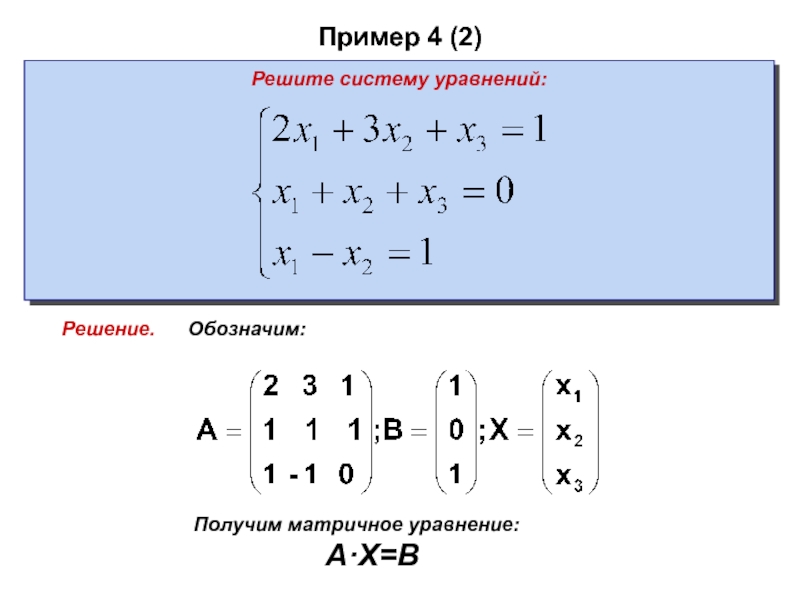
- 60. Пример 4 (2)Решите систему уравнений:Обозначим:Получим матричное уравнение:A·X=BРешение.
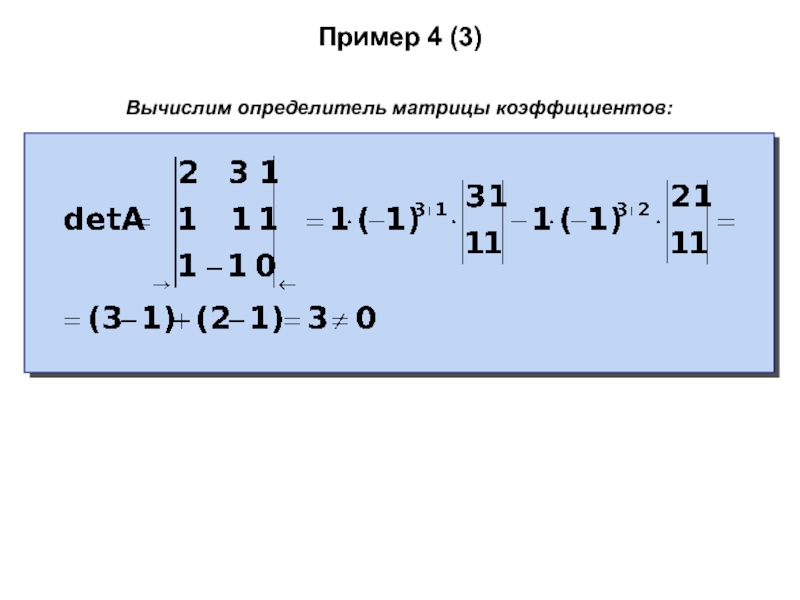
- 61. Пример 4 (3)Вычислим определитель матрицы коэффициентов:
- 62. Пример 4 (4)Найдем алгебраические дополнения элементов:
- 63. Пример 4 (5)
- 64. Пример 4 (6)
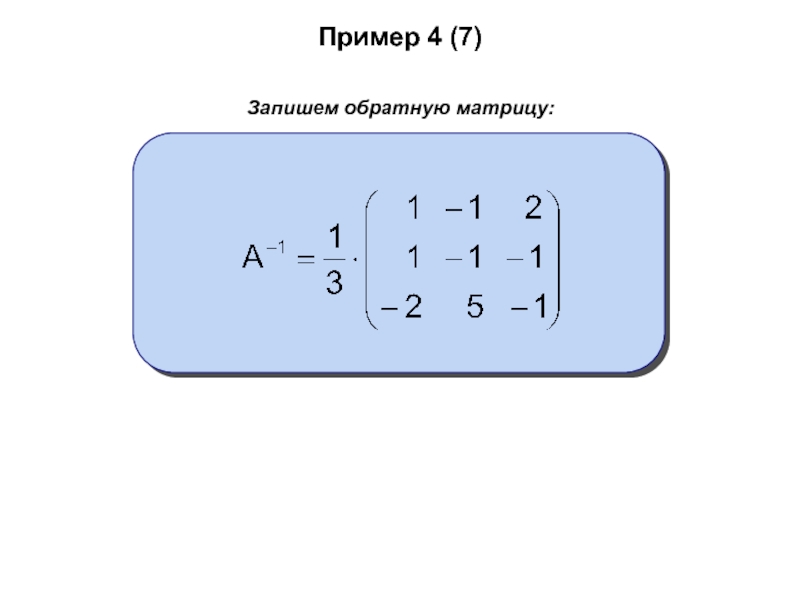
- 65. Пример 4 (7)Запишем обратную матрицу:
- 66. Пример 4 (8)По формуле X=A-1·B найдем решениематричного уравнения:
- 67. Правило Крамера (1)Пусть m=nПусть detA = Δ ≠ 0Рассмотрим систему
- 68. Правило Крамера (2)Пусть m=nПусть detA = Δ ≠ 0Рассмотрим системуJ – столбецОбозначим
- 69. Правило Крамера (3)Решение системы
- 70. Пример 5 (1)Решите систему уравнений:
- 71. Пример 5 (2)Решение. Запишем определитель из коэффициентов уравнения:Решите систему уравнений:
- 72. Пример 5 (3)Решение. Запишем определитель из коэффициентов уравнения:Решите систему уравнений:Вычислим определители Δ1 и Δ2:
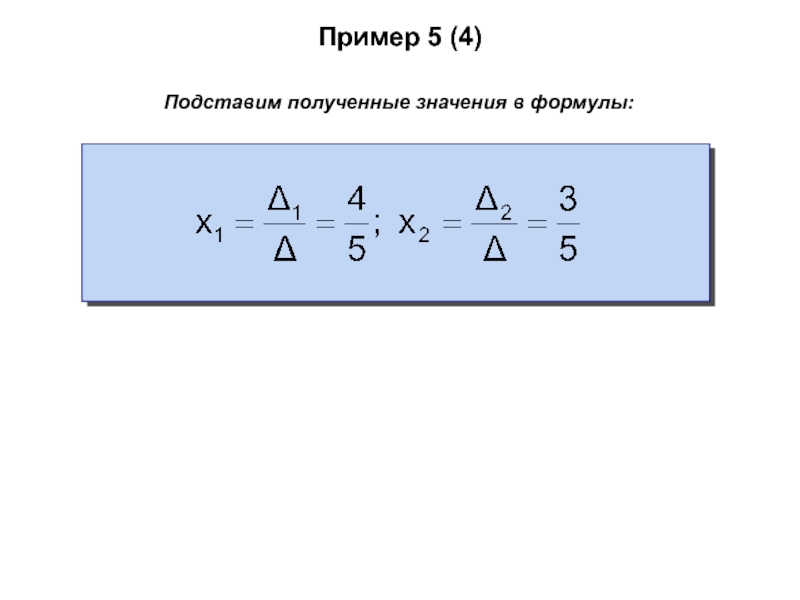
- 73. Пример 5 (4)Подставим полученные значения в формулы:
- 74. Занятие 5.РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМГАУССА.
- 75. Метод Гаусса – метод последовательного исключения переменных.Пусть задана система:
- 76. 1. Составим расширенную
- 77. Пример 6. Решить систему уравнений методом Гаусса:
- 78. Составим расширенную матрицу и приведём её к треугольному виду с помощью элементарных преобразований.
- 79. Получаем:Вернёмся к системе уравнений Ответ: х1=1; х2=2; х3=-2
- 80. Метод Гаусса применим к любой системе линейных
- 81. Решение: Составим расширенную матрицу и преобразуем её.
- 82. Получаем: Мы видим, что последнее уравнение будет 0
- 83. Пример 8. Решить систему: Решение: Составим расширенную матрицу и преобразуем её.
- 84. Получаем:Вернёмся к системе уравнений.
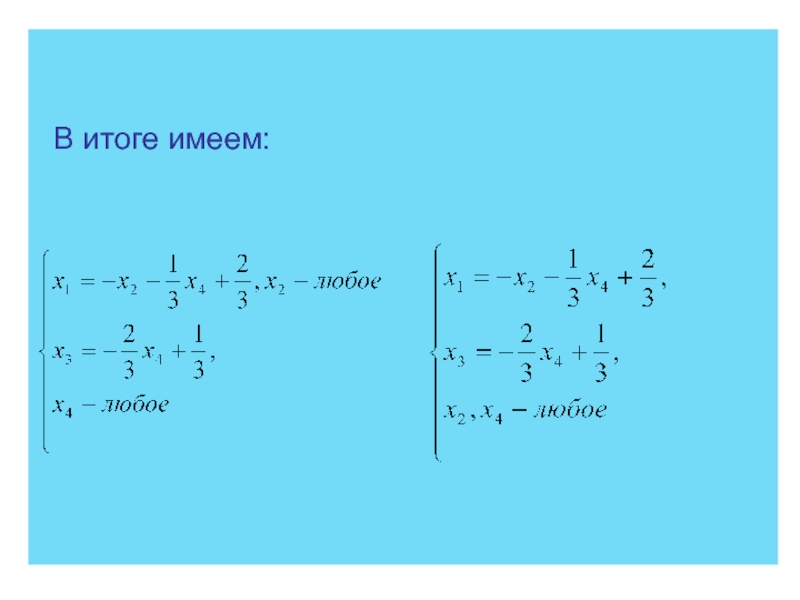
- 85. В итоге имеем:
- 86. Рассмотрим случай, когда заданная система состоит из
- 87. Решение: Эта система однородных уравнений; причём число уравнений меньше числа неизвестных (3
- 88. Вернёмся к системе уравнений: Как мы видим,
- 89. Занятие 7Решение систем линейных уравненийметодом Крамера
- 90. Пусть дана система: Составим матрицу А из коэффициентов при неизвестных
- 91. Найдём определитель det A=Правило Крамера. Если
- 92. Решение системы линейных уравнений :Находим определитель системы
- 93. Пример 1. Решить систему: Решение:
- 94. Пример 2. Решить систему: Решение:
- 95. Находим: х1,
- 96. Применяем формулы Крамера:х1=1; х2=2; х3=-2
- 97. Занятие 9РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ОБРАТНОЙ МАТРИЦЫ
- 98. Дана система:Матричная запись системы линейных уравнений имеет
- 99. Пример 12. Решить с помощью обратной матрицы
- 100. Вычислим алгебраические дополнения для элементов каждой строки.
- 101. Составляем обратную матрицу:Отсюда:
- 102. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема 5. «Системы линейных уравнений»
Основные понятия:
Общий вид, основные понятия, матричная
форма
Слайд 21. Общий вид, основные понятия, матричная форма
Система m линейных уравнений
с n неизвестными имеет вид:
где
коэффициенты при неизвестных,
свободные
коэффициенты.
Слайд 3
Если , то СЛУ называется однородной.
Если хотя бы один
, то СЛУ называется
неоднородной.Система, имеющая хотя бы одно решение, называется совместной, и система, не имеющая ни одного решения, называется несовместной.
Слайд 4Совместная система называется определенной, если она имеет единственное решение, и
неопределенной, если имеет более одного решения.
Выражение «решить СЛУ» означает выяснить,
совместна СЛУ или несовместна, в случае совместности – найти все ее решения.Решение СЛУ называется упорядоченная совокупность чисел , подстановка которых в СЛУ обращает каждое ее уравнение в тождество.
Слайд 5
Любую СЛУ можно представить в матричном виде:
На основании согласованности матрицы
А с матрицей Х:
- матричный вид исходной СЛУ.
Слайд 6
2. Методы решения СЛУ
Метод последовательного исключения неизвестных (Метод Гаусса)
Метод Крамера
(с помощью определителей)
Метод обратной матрицы
Карл Фридрих Гаусс (1777-1855) - немецкий
математикГабриэль Крамер (1704-1752) – швейцарский математик
Слайд 7Метод последовательного исключения неизвестных (Метод Гаусса)
Рассмотрим СЛУ:
Данный метод применим к
СЛУ любой размерности.
Слайд 8Алгоритм метода:
1 уравнение умножаем на
и складываем со вторым уравнением системы;
1
уравнение умножаем на и складываем с третьим уравнением системы;И т.д.
В результате чего придем к системе, эквивалентной исходной системе уравнений.
Слайд 91 случай:
В этом случае СЛУ имеет единственное решение.
Значение
находится из последнего уравнения, значение
из предпоследнего уравнения и т.д., значение находится из первого уравнения.
Слайд 102 случай:
В этом случае СЛУ имеет бесконечно много решений.
Из последнего
уравнения выражается одно из неизвестных через остальные неизвестные и т.д.
Слайд 113 случай:
В этом случае СЛУ несовместна (не имеет решений), т.к.
последнее уравнение является противоречивым.
Замечание. Метод Гаусса удобно осуществлять в матричном
виде.Слайд 12Метод Гаусса
(метод исключения неизвестных)
Две системы называются эквивалентными (равносильными), если
их решения совпадают.
К эквивалентной системе можно перейти с помощью
элементарных преобразований расширенной матрицы этой системы.Слайд 13
Схема действий метода Гаусса:
а) из всех уравнений системы кроме
первого исключается неизвестное x1;
б) из всех уравнений системы
кроме первого и второго исключается неизвестное x2; в) из всех уравнений системы кроме первого, второго и третьего исключается неизвестное x3 и т.д. г) Обратным ходом из последнего уравнения находят одну неизвестную, из предпоследнего – следующую и т.д.
Слайд 14
Исключение неизвестных обычно осуществляют элементарными преобразованиями строк расширенной матрицы СЛУ.
В результате расширенная матрица СЛУ приводится к трапецеидальному виду,
который
позволяет легко выделить базисный минор основной матрицы системы.Слайд 15
Неизвестные, коэффициенты при которых вошли в базисный минор называются базисными
неизвестными.
Неизвестные, коэффициенты при которых не вошли в базисный минор,
называются свободными неизвестными.Слайд 16
Если n – число неизвестных системы, r – её ранг,
то
r неизвестных системы – базисные,
k = n –
r свободные.Слайд 17
Если ранг основной и расширенной матриц СЛУ совпадает с числом
неизвестных СЛУ, то свободных неизвестных нет. В этом случае СЛУ
имеет единственное решение (определённая СЛУ). Если ранги основной и расширенной матриц СЛУ равны, но меньше числа неизвестных СЛУ, то СЛУ неопределённая. В этом случае находят общее решение СЛУ.Слайд 18
Решение СЛУ, в котором базисные неизвестные выражены через свободные неизвестные,
называется общим решением СЛУ. Решение, которое получается из общего путём присваивания
свободным неизвестным числовых значений, называется частным решением СЛУ.Слайд 19
Общее решение системы линейных уравнений можно получить, руководствуясь, например, следующим
планом:
а) выбрать базисный минор (обычно это минор, под главной диагональю
которого – все нули);б) перенести свободные неизвестные к свободным членам, то есть в правые части уравнений;
в) обратным ходом метода Гаусса выразить базисные неизвестные через свободные неизвестные.
Слайд 20
Фундаментальной системой частных решений системы n однородных линейных уравнений (СОЛУ)
называется система линейно независимых частных решений, число решений в которой
равно числу k = n – r свободных неизвестных системы,где r - ранг основной матрицы системы.
Слайд 21
Фундаментальную систему частных
решений (ФСЧР СОЛУ) получают обычно, последовательно приравнивая свободные
неизвестные элементам строк единичной матрицы порядка
.Замечание. ФСЧР СОЛУ можно получить также, приравнивая свободные неизвестные элементам строк произвольной квадратной матрицы А порядка k = n – r, если
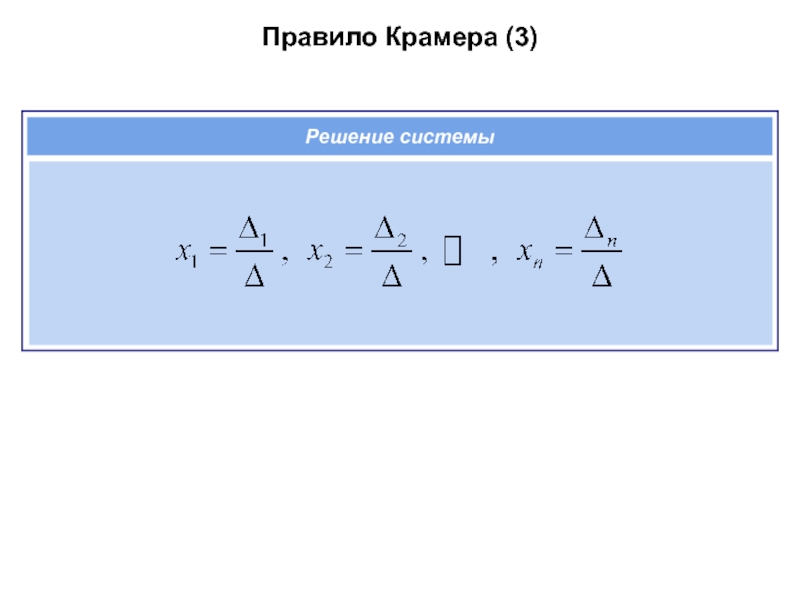
Слайд 25Метод Гаусса (3)
Рассмотрим систему
С помощью элементарных преобразований
приводим ее к равносильной
системе ступенчатого вида:
Слайд 26Метод Гаусса (4)
Возможен один из следующих случаев:
1) система не имеет
решений
(система несовместна);
2) система имеет
единственное решение;
3) система имеет бесчисленное
множество решений.
Слайд 392) Метод Крамера
Метод основан на вычислении определителей, поэтому применим к
СЛУ размерности nxn.
Рассмотрим СЛУ:
Слайд 40Введем следующие обозначения:
Теорема. Если
, то СЛУ имеет единственное решение
, где . (Формулы Крамера)Слайд 413) Метод обратной матрицы
Метод основан на нахождении обратной матрицы, поэтому
применим к СЛУ размерности nxn.
Рассмотрим СЛУ в матричном виде:
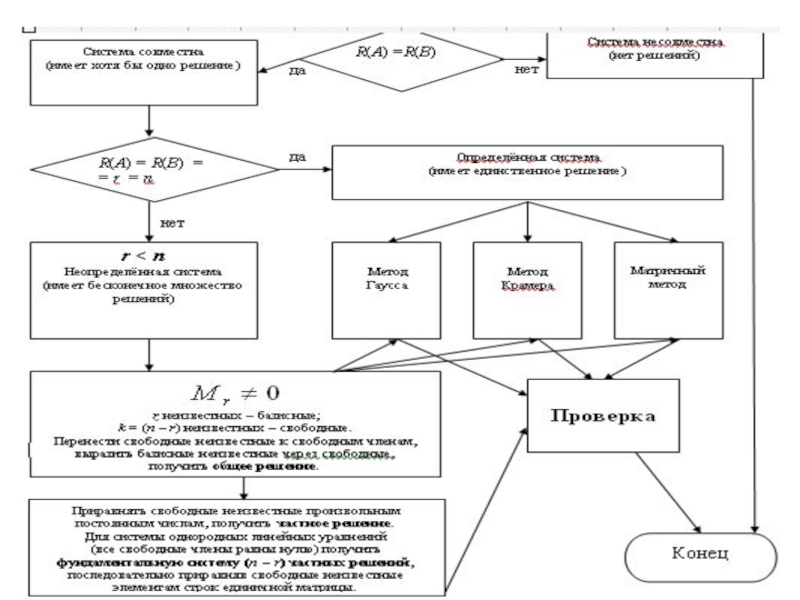
Слайд 423. Теорема Кронекера-Капелли
Помимо метода Гаусса, на вопрос совместна ли СЛУ
или нет можно воспользоваться теоремой Кронекера-Капелли.
Теорема Кронекера-Капелли. Для совместимости
СЛУ необходимо и достаточно, чтобы ранг ее матрицы был равен рангу расширенной матрицы.Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение.
Если ранг матрицы совместной системы меньше числа неизвестных, то множество ее решений является бесконечным.
Слайд 44Системы линейных уравнений (1)
Системой m линейных уравнений
с n неизвестными
называется система
вида
где aij и bi ─ числа, xi – неизвестные.
,
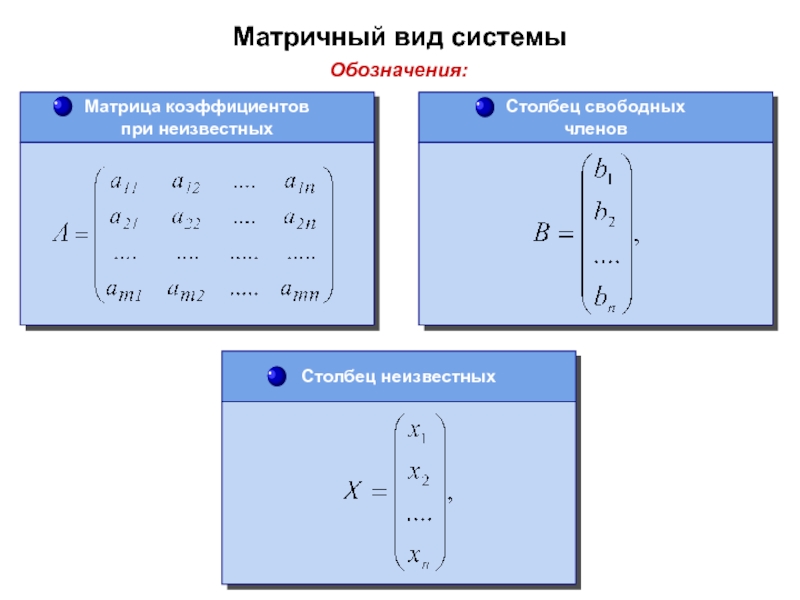
Слайд 49Матричный вид системы
Обозначения:
Матрица коэффициентов
при неизвестных
Столбец неизвестных
Столбец свободных
членов
Слайд 71Пример 5 (2)
Решение.
Запишем определитель из коэффициентов уравнения:
Решите систему уравнений:
Слайд 72Пример 5 (3)
Решение.
Запишем определитель из коэффициентов уравнения:
Решите систему уравнений:
Вычислим определители
Δ1 и Δ2:
Слайд 76
1. Составим расширенную матрицу.
2.
С помощью элементарных преобразований строк расширенную матрицу приведём к треугольному
(ступенчатому) виду.3. Вернувшись к системе уравнений, находим неизвестные.
Элементарными преобразованиями матрицы называют:
Умножение какой-нибудь строки (столбца) на отличное от нуля число.
Прибавление к какой-нибудь строке (столбцу) другой её строки (столбца), умножение на любое число, отличное от нуля.
Перестановку местами любых двух строк.
Слайд 78Составим расширенную матрицу и приведём её к треугольному виду с
помощью элементарных преобразований.
Слайд 80 Метод Гаусса применим к любой системе линейных уравнений. При этом
система будет несовместной, т.е. не иметь решения, если после преобразований
мы получим уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля.Пример 7. Решить систему:
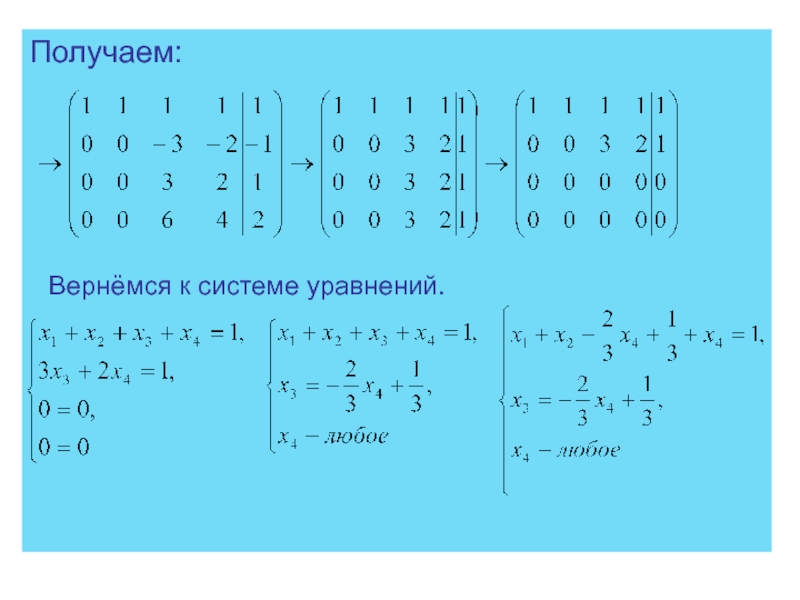
Слайд 82Получаем:
Мы видим, что последнее уравнение будет 0 = 2. Значит,
заданная система
будет несовместной, т.е. не иметь решения. Совместная система
будет неопределённой, (то есть иметь решений больше, чем одно), если после преоб-разований матрица приводится к трапе-циевидному виду. Слайд 86 Рассмотрим случай, когда заданная система состоит из линейных однородных уравнений,
то есть уравнений, свободные члены которых равны нулю. Такая система
всегда совместна, так как обладает нулевым решением (0; 0; …; 0). Если в системе линейных однородных уравнений число уравнений меньше числа неизвестных, то эта система обладает, помимо нулевого решения, также и ненулевыми решениями. Таких решений будет бесконечно много.Пример 9. решить систему:
Слайд 87Решение:
Эта система однородных уравнений; причём число уравнений меньше числа
неизвестных (3
(так как свободные члены равны нулю) и преобразуем её.
Слайд 88Вернёмся к системе уравнений:
Как мы видим, с помощью метода
Гаусса можно решить любую систему, содержащую любое число линейных уравнений
с любым числом неизвестных. Это один из самых эффективных методов решения систем линейных уравнений.Слайд 91Найдём определитель
det A=
Правило Крамера. Если m=n и
det A≠0, то система совместна и имеет единственное решение
где det Ai – определитель, полученный из det A заменой i-ого столбца столбцом свободных членов.Слайд 92Решение системы линейных уравнений :
Находим определитель системы
.
Вычисляем определители х1, x2, …
Возможны три случая:
Если
≠0, то система имеетединственное решение:
Если =0, но хотя бы один из определителей хi не равен нулю, то система не имеет решений.
Если =0, х1=0, х2=0, …, хn=0, то система имеет бесконечное множество решений.
Слайд 98Дана система:
Матричная запись системы линейных уравнений имеет вид:
АХ=В Отсюда: Х= ,
где матрица, обратная матрице А.