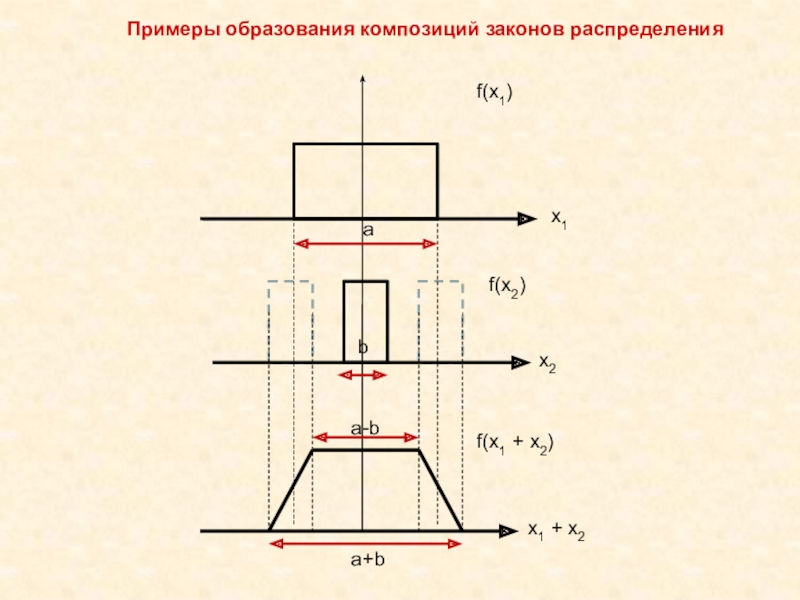
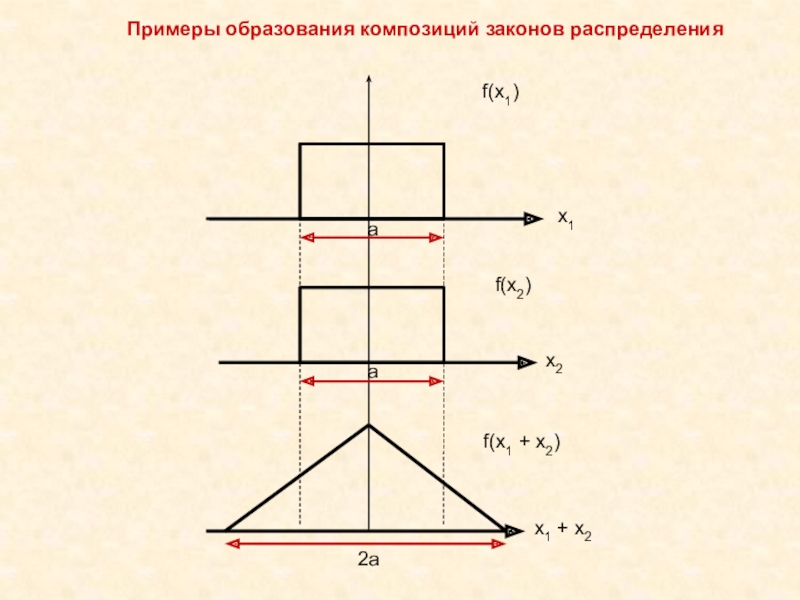
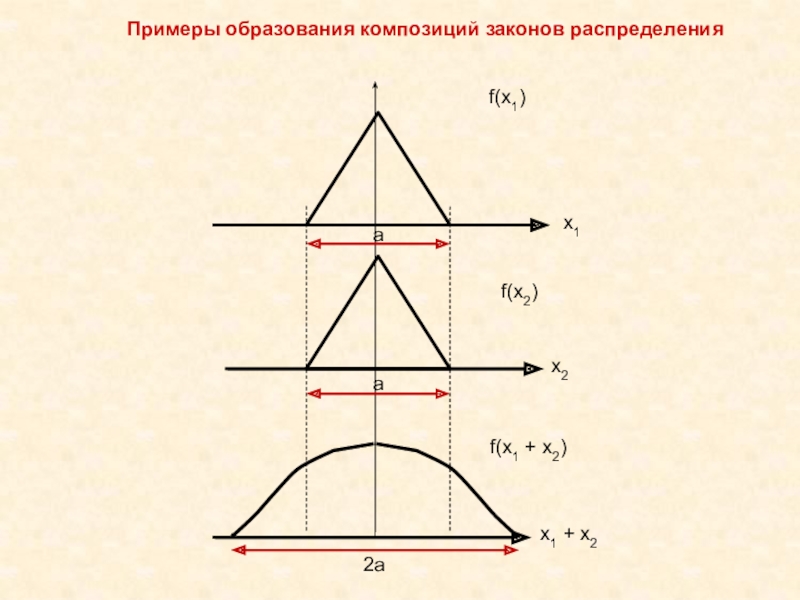
и поэтому не могут быть исключены из результатов измерений, как
систематические погрешности.Случайной называют такую величину, которая в результате опыта может принимать то или иное значение, неизвестно заранее ‑ какое именно.
Дискретные случайные величины – принимающие отделенные друг от друга значения, которые можно заранее перечислить.
Непрерывные случайные величины - величины, возможные значения которых непрерывно заполняют некоторый промежуток.


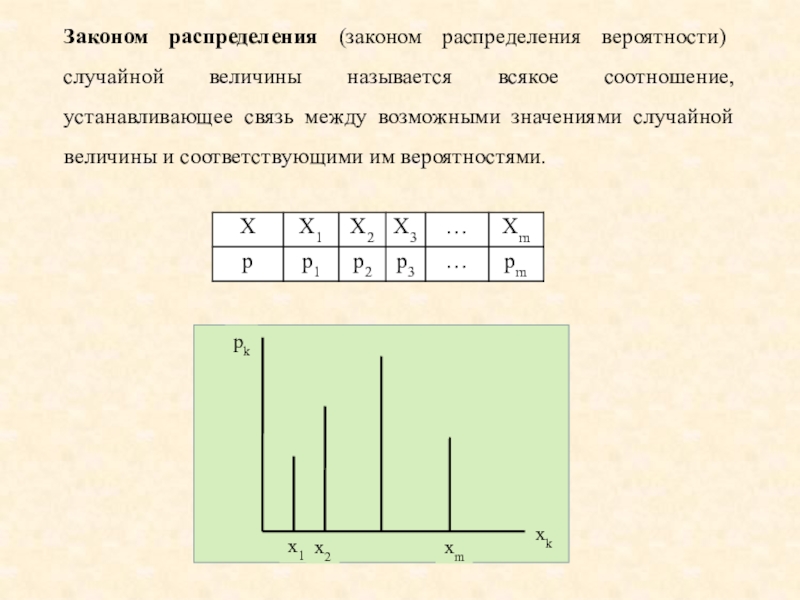




![Случайные погрешности
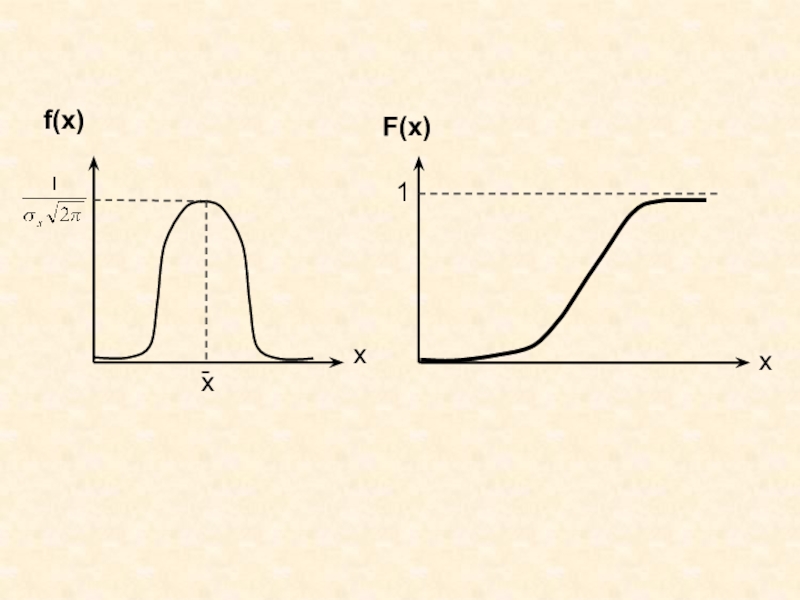
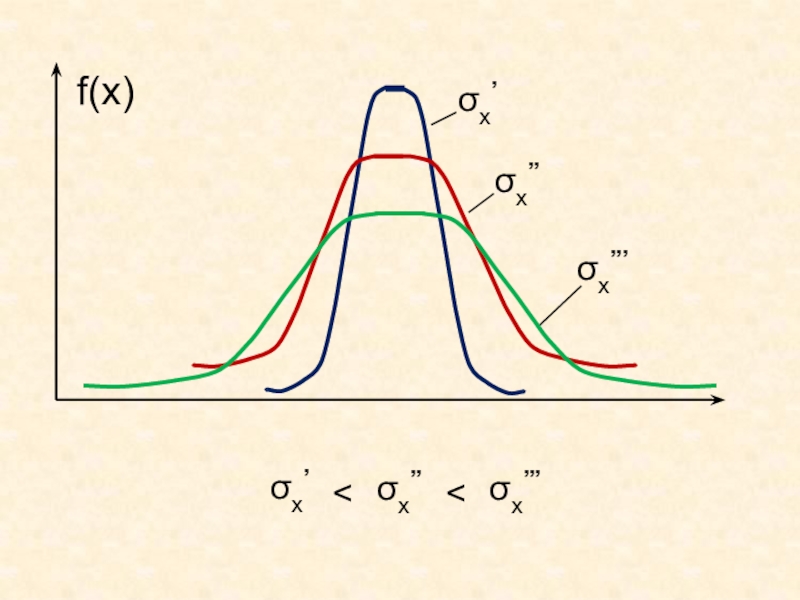
Случайные погрешности неопределенны по своему значению и C использованием дифференциальной функции распределения вероятность попадания случайной величины X в C использованием дифференциальной функции распределения вероятность попадания случайной величины X в интервал [x1, x2] равна :Перечень стандартных](/img/tmb/6/599658/9f99c45a57e9b36276663c3f43eac834-800x.jpg)