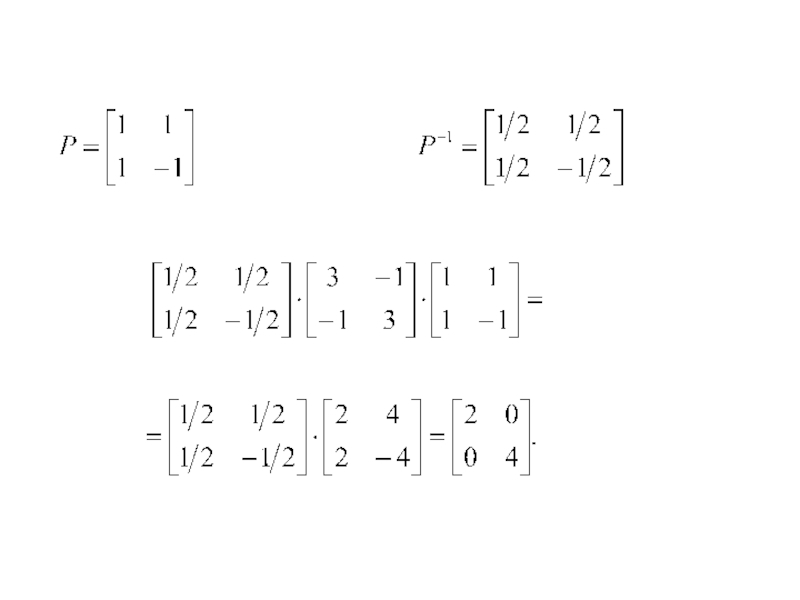Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Собственные векторы и собственные значения линейного оператора
Содержание
- 1. Собственные векторы и собственные значения линейного оператора
- 2. 1. ОпределенияОпределение 1.1. Оператор φ n–мерного векторного
- 3. 2. Нахождение собственных значений и собственных векторов
- 4. Нахождение собственных значений и собственных векторов линейного
- 5. Определения 2.1. Матрица A–λI называется
- 6. Теорема 2.2: (Свойства подобных матриц)Пусть матрицы S и T подобны, тогдаДоказательство.
- 7. Таким образом, число λ является
- 8. Пример
- 9. Пример вычисления СЗ для матрицы
- 10. 3.Свойства собственных векторов 1. Лемма 3.1. Каждый собственный
- 11. Лемма 3.2. Если v1 и v2 –
- 12. Следствия 3.3.а) каждому собственному значению λ соответствует беско-
- 13. Лемма 3.4. Собственные векторы x1,x2,…,xk оператора φ,
- 14. Точно также применим оператор φ, умножим на
- 15. Следствия 3.5:а) линейный оператор, действующий в n-мерном
- 16. Теорема 3.6. Характеристический многочлен линейного оператора не
- 17. Теорема 3.8 (необходимое и достаточное условие диагональ-
- 18. Теорема 3.9. (Условие диагонализуемости оператора)n×n матрица A
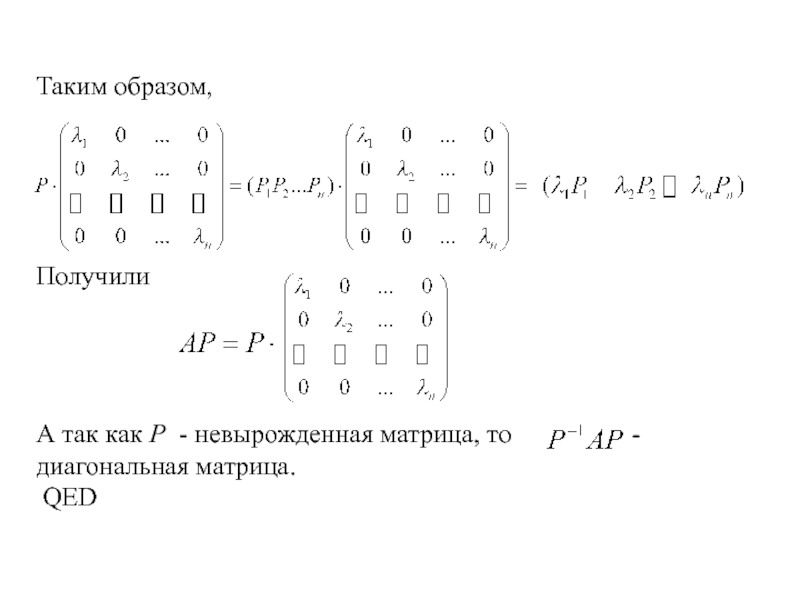
- 19. Таким образом,
- 20. Таким образом,ПолучилиА так как Р - невырожденная
- 21. Критерий диагонализируемости оператора: оператор φ диагонализируем тогда
- 22. Пример
- 23. Пример (продолжение)
- 24. Слайд 24
- 25. 4.Линейный оператор с простым спектромОпределение 4.1 Набор
- 26. Пример: матрица
- 27. Слайд 27
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Собственные векторы и собственные значения линейного оператора
1.Определение
2. Нахождение СЗ и
СВ линейного оператора
Слайд 21. Определения
Определение 1.1. Оператор φ n–мерного векторного пространства V называется
диагонализируемым, если в V существует базис, в котором матрица линейного
оператора диагональная.Определение 1.2. Пусть φ – оператор пространства V. Если для некоторого ненулевого вектора v∈V и числа λ имеем
φ(v)= λ·v,
то число λ называется собственным значением оператора φ , а вектор v называется собственным вектором оператора φ , относящимся к собственному значению λ.
Слайд 32. Нахождение собственных значений и
собственных векторов линейного оператора
Пусть φ
– оператор n-мерного пространства V , v – собственный вектор
оператора φ , относящийся к собственному значению λ , т.е. φ(v)= λ·v.Пусть { b1,b2,…,bn }– базис V ,
A – матрица линейного оператора φ в базисе { b1,b2,…,bn } и v = c1b1 + c2b2 + … + cnbn
⇔
φ(v)= φ(c1b1 + c2b2 + … + cnbn v)= c1φ(b1)+ c2φ(b2 )+ … + cnφ(bn) =
Слайд 4Нахождение собственных значений и
собственных векторов линейного оператора (продолжение)
Получили:
v – собственный
вектор оператора φ , относящийся к соб- ственному значению λ
⇔ его координаты c1,c2,…,cn являются решением (нетривиальным) системы линейных однородных уравнений (A–λI)X=O.Слайд 5 Определения 2.1.
Матрица A–λI называется характеристической матрицей оператора
φ (матрицы A) .
Определитель характеристической матрицы, т.е. det(A–λI)
– многочлен степени n относительно переменной λ . Многочлен det(A–λI) называют характеристическим много- членом оператора φ (матрицы A).
Корни многочлена det(A–λI) называют характеристи- ческими корнями оператора φ (матрицы A).
Слайд 7
Таким образом, число λ является собственным значением оператора
φ тогда и только тогда, когда оно является его характеристическим
корнем.Слайд 103.Свойства собственных векторов
1. Лемма 3.1. Каждый собственный вектор v оператора
φ относится к единственному собственному значению.
Доказательство (от противного).
Пусть вектор v
относится к двум различным собственным значениям - и :Но вектор v – ненулевой, поэтому
QED
Слайд 11Лемма 3.2. Если v1 и v2 – собственные векторы оператора
φ, относящиеся к одному и тому же собственному значению λ
, то их линейная комбинация a·v1+b·v2 – собственный вектор оператора φ , относящийся к тому же собственному значению.Доказательство.
φ (a·v1+b·v2 ) =
a φ (v1)+b φ(v2 ) =
a λv1+b λ v2 =
λ (a·v1+b·v2 )
QED
Слайд 12Следствия 3.3.
а) каждому собственному значению λ соответствует беско-
нечное множество собственных векторов;
б) если
к множеству всех собственных векторов x оператора φ, относящихся к
собственному значению λ, присоединить нулевой вектор, то получится подпространство простран- ства V. Оно называется собственным подпространством оператора и обозначается Vλ.Слайд 13Лемма 3.4. Собственные векторы x1,x2,…,xk оператора φ, относящиеся к попарно
различным собственным значениям λ1,λ2,…, λk , линейно независимы.
Доказательство (от противного).
Предположим x1,x2,…,xk ЛЗ: с1x1+с2x2+…+ сk xk =0 и хотя бы один из коэффициентов – ненулевой, например,
сk - ненулевое число.
Проведем две операции: применим оператор φ и умножим на λ1
φ (с1x1+с2x2+…+ сk xk) = с1λ1x1+с2λ2x2 …+ сk λk xk =0 и
λ1(с1x1+с2x2+…+ сk xk) = с1λ1x1+с2λ1x2 …+ сk λ1 xk =0.
с1λ1x1+с2λ2x2 …+ сk λk xk =0
с1λ1x1+с2λ1x2 …+ сk λ1 xk = 0
Вычтем из первого второе соотношение:
с2 (λ2-λ1)x2…+ сk ( λk -λ1)xk =0.
Слайд 14Точно также применим оператор φ, умножим на λ2
φ(с2 (λ2-λ1)x2…+
сk ( λk -λ1)xk) =с2λ2 (λ2-λ1)x2…+сk λk ( λk -λ1)xk
=0 иλ2(с2 (λ2-λ1)x2…+ сk ( λk -λ1)xk) = с2λ2 (λ2-λ1)x2…+с2 λk ( λk -λ1)xk =0
и вычтем:
с3 (λ3-λ1) (λ3-λ2) x3…+ сk ( λk -λ1) ( λk –λ2) xk =0.
Продолжая так, в конце концов получим
сk ( λk -λ1) ( λk –λ2) … ( λk –λk-1) xk =0.
Собственные значения различны, собственный вектор – ненулевой.
Отсюда следует сk =0, что противоречит предположению. QED
Слайд 15Следствия 3.5:
а) линейный оператор, действующий в n-мерном линейном пространстве V,
не может иметь более n собственных значений;
б) в пространстве
может существовать базис, хотя бы часть которого – собственные векторы оператора. Слайд 16
Теорема 3.6. Характеристический многочлен линейного оператора не зависит от выбора
базиса, то есть является инвариантом линейного оператора ( таким образом,
подобные матрицы имеют один и тот же характеристический многочлен).Следствие 3.7. Множество собственных значений линейного оператора не зависит от выбора базиса, то есть является инвариантом линейного оператора ( таким образом, подобные матрицы имеют один и тот же набор собственных значений).
Доказательство.
Пусть Р и Q – матрицы одного и того же линейного
оператора в различных базах. Тогда
Слайд 17Теорема 3.8 (необходимое и достаточное условие диагональ- ности матрицы оператора) .
Матрица A оператора φ в базисе {b1,b2,…,bn} имеет диагональный вид
⇔ все базисные векторы bi являются собственными векторами этого оператора.Доказательство.
QED
Слайд 18
Теорема 3.9. (Условие диагонализуемости оператора)
n×n матрица A подобна диагональной т.и
т.т.к. она имеет n линейно независимых собственных векторов.
А подобна диагональной матрице D. Тогда существует невырожденная матрица Р такая что . Пусть - столбцы матрицы Р, а - диагональные элементы матрицы D .
Доказательство.
С другой стороны,
Слайд 19Таким образом,
и столбцы матрицы Р являются собственными векторами матрицы А (матричный линейный оператор). В силу невырожденности P, все эти векторы линейно независимы.
А имеет n линейно независимых собственных столбцов,
обозначим их , относящихся к собственным значениям
Обозначим , тогда Р – невырожденная матрица и
Слайд 21
Критерий диагонализируемости оператора: оператор φ диагонализируем тогда и только тогда,
когда в пространстве V существует базис, каждый из векторов которого
является собственным вектором оператора .Слайд 254.Линейный оператор с простым спектром
Определение 4.1 Набор всех собственных значений
оператора называется спектром оператора.
Определение 4.2. Линейный оператор n-мерного векторного
пространства, имеющий n попарно различных собственных значений, называется оператором с простым спектром. Следствие 4.3.
(1) Матрица оператора с простым спектром подобна диагональной матрице, у которой на диагонали стоят собственные значения оператора.