Разделы презентаций

Содержание: Элементарная классическая логика. Семантика логических

Содержание

Элементарная классическая логика. Семантика логических знаков.Введение: Высказывания и формы высказываний.Тема 1: Логические союзы.Тема 2: Язык логики высказываний.Тема 3: Правильно построенное высказывание.Тема 4: Формула логики высказываний.Тема 5: Семантика логических знаков.Тема 6: Семантическая

Слайды и текст этой презентации

Слайд 1Содержание:
Элементарная классическая логика. Семантика логических знаков.
Исчисление истинностных значений логических формул. Тождественно-истинные

и тождественно-ложные формулы.
Двойственность логических формул. Равносильные формулы.
Понятие нормальной формы.
Логическое следование.

Естественный вывод в логике высказываний.

Исчисление предикатов. Символизация естественного языка.







Содержание:Элементарная классическая логика. Семантика логических знаков.Исчисление истинностных значений логических формул. Тождественно-истинные и тождественно-ложные формулы.Двойственность логических формул. Равносильные

Слайд 2Элементарная классическая логика. Семантика логических знаков.
Введение: Высказывания и формы высказываний.
Тема

1: Логические союзы.
Тема 2: Язык логики высказываний.
Тема 3: Правильно построенное

высказывание.

Тема 4: Формула логики высказываний.

Тема 5: Семантика логических знаков.

Тема 6: Семантическая таблица отрицания.

Тема 7: Семантическая таблица исключающей (строгой) дизъюнкции.

Модуль 1.







Элементарная классическая логика. Семантика логических знаков.Введение: Высказывания и формы высказываний.Тема 1: Логические союзы.Тема 2: Язык логики высказываний.Тема

Слайд 3 Высказыванием называют предложение,

выражающее суждение. Если суждение, составляющее содержание (смысл) некоторого высказывания, истинно,

то о данном высказывании говорят, что оно истинно. Сходным образом ложным называют такое высказывание, которое является выражением ложного суждения.
Будем считать, что:
- всякое высказывание истинно или ложно
- ни одно высказывание не является сразу истинным и ложным.
Истинность и ложность называют логическими, или истинностными, значениями высказываний. Если высказывание истинно, то говорят, что оно имеет логическое значение
"истина", а если высказывание ложно, то говорят, что оно имеет логическое значение "ложь".

Введение: Высказывания и формы высказываний.







Высказыванием называют предложение, выражающее суждение. Если суждение, составляющее содержание (смысл)

Слайд 4 Слова: не; неверно, что; и; или; если..., то; тогда и

только тогда, когда; либо...,
либо; несовместно; ни..., ни и их

ближайшие синонимы, называют логическими союзами (связками),
Cлова: для всех... имеет место, что; для некоторых... имеет место, что и их ближайшие синонимы, называют кванторами. Логические союзы и кванторы называют логическими постоянными
Логика занимается установлением точного смысла этих слов и общих законов их употребления.
Высказывания, не содержащие логических постоянных, называют элементарными высказываниями.
Высказывания, которые содержат логические постоянные, называют сложными высказываниями.
Логическое значение сложного высказывания определяется логическим значением входящих в его состав элементарных высказываний и теми логическими постоянными, с помощью которых оно построено.

Логические союзы.







Слова: не; неверно, что; и; или; если..., то; тогда и только тогда, когда; либо..., либо; несовместно; ни...,

Слайд 5 Существуют формы высказываний с двумя предметными переменными (с двумя пробелами);

например, х старше у (...старше -...); х> у (...>...) и

т. п. Если вместо всех предметных переменных подставить единичные термины, то получим истинные или ложные высказывания. Формы высказываний с двумя предметными переменными выражают условия, которым одни упорядоченные пары объектов удовлетворяют, а другие - не удовлетворяют. С помощью каждой из них можно определить класс упорядоченных пар объектов, связанных соответствующим отношением.

Логические союзы.







Существуют формы высказываний с двумя предметными переменными (с двумя пробелами); например, х старше у (...старше -...); х>

Слайд 6 Если в форме высказывания, содержащей несколько предметных переменных, осуществить подстановку

только для одной из них, то получится форма высказывания с

меньшим числом предметных переменных.
С помощью логических союзов формы высказывания можно связывать как друг с другом, так и с высказываниями.
Одна и та же предметная переменная может входить в форму высказывания два, три и большее число раз.
Осуществляя подстановку, необходимо следить за тем, чтобы вместо одной и той же предметной переменной на всех местах, где она входит в данную форму высказывания, подставлялось одно и то же собственное имя.
В результате подстановки единичных терминов вместо всех предметных переменных форма высказывания превращается в истинное или ложное высказывание. Но формы высказываний могут превращаться в высказывания и в результате присоединения к ним кванторов.

Логические союзы.







Если в форме высказывания, содержащей несколько предметных переменных, осуществить подстановку только для одной из них, то получится

Слайд 7 В формализованном языке элементарной логики базовым понятием является понятие высказывания.


- предложение есть понятие грамматическое,

т.е. грамматическая форма выражения мысли, суждение - в соответствии с традиционной логикой - есть форма мышления, в которой отражаются отношения между предметами и их признаками посредством утверждения или отрицания;
- высказывание же - это такой логический объект (объект анализа логической теории), который может быть истинным или ложным.
Встречаются повествовательные предложения, образованные путем видоизменения некоторого предложения с помощью частицы "не" или путем связывания предложений с помощью слов "и", "или" (в различных его смыслах), "если..., то...", "тогда и только тогда, когда" ("если и только если"). Эти пять частиц и словосочетаний называют пропозициональными связками, или высказывание образующими операторами.
Каждый из высказывание образующих операторов имеет в теоретической логике свое специальное название, и образованное с его помощью соответствующее высказывание получает то же название.
Смысловой союз, который в языке имеет вид "не"/"неверно, что", называется отрицанием.

Логические союзы.







В формализованном языке элементарной логики базовым понятием является понятие высказывания. - предложение

Слайд 8 Союз "и" (может быть "да", "но", "а" в значении "и")

называется конъюнкцией.
Союз "или" принято называть "дизъюнкцией", которая имеет два

значения: слабое и сильное. Слабая дизъюнкция связывает такие высказывания, которые могут быть истинны одновременно. Сильная, или строгая дизъюнкция имеет смысл "либо..., либо...", т.е. то, о чем говорится в каждом из высказываний, исключает другое.

Логические союзы.







Союз

Слайд 9 Из двух высказываний можно построить одно, типа "если..., то...", которое

называется импликацией. Высказывание, непосредственно следующее за "если", есть антецедент импликации,

а высказывание, непосредственно следующее за "то", - консеквент импликации.
Оператор, выражаемый посредством "если и только если" ("тогда и только тогда, когда"), называется эквиваленцией (безусловным высказыванием). Выражение "А, если и только если В" рассматривается как имеющее то же значение, что и "Если А, то В, и если В, то А".

Логические союзы.







Из двух высказываний можно построить одно, типа

Слайд 10 Логика высказываний может быть построена так. Прежде всего для этого

сначала введем понятие языка логики высказываний, задаваемого алфавитом языка и

понятием правильно построенного высказывания.
Язык логики высказываний включает в себя следующие символы:
- р, q, r,... - пропозициональные буквы, имеющие значением простые высказывания;
- высказывание образующие операторы: - (отрицание), /\ (конъюнкция),
\/ (слабая дизъюнкция ), ( сильная дизъюнкция ), → ( импликация ),
↔ ( эквиваленция ) ;
- вспомогательные символы, в качестве которых используются круглые скобки.

Язык логики высказываний.







Логика высказываний может быть построена так. Прежде всего для этого сначала введем понятие языка логики высказываний, задаваемого

Слайд 11 Понятие правильно построенного высказывания (ППВ):
1. Всякая пропозициональная буква есть

(простое) высказывание (ППВ).
2. Если А и В -

ППВ, то (А/\В),(АVВ),(А→В),(А↔В), (А В) - также ППВ.
3. Всякая последовательность символов языка логики высказываний есть ППВ только в силу пунктов 1 и 2.
Язык логики высказываний - это искусственный язык, предназначенный для анализа логической структуры сложных высказываний.
Роль структурных образований, аналогичных элементарным и сложным высказываниям, в этом языке играют формулы.
Формулы - это такие конечные последовательности знаков алфавита, которые построены по определенным правилам и образуют законченные выражения языка логики высказываний.

Правильно построенное высказывание.







Понятие правильно построенного высказывания (ППВ): 1. Всякая пропозициональная буква есть (простое) высказывание (ППВ). 2. Если А

Слайд 12 Определение формулы логики высказываний:
- пропозициональная переменная есть формула;

- если А произвольная формула, то [читается: "не А"

или "неверно, что А"] - тоже формула;
- если А и В - произвольные формулы, то (А/\В) [читается: "А и В"], (А\/В) [читается: "А или В" (А→В) [читается: "если А, то В"], (А↔В) [читается: "А тогда и только тогда, когда В"], (А В) [читается: "либо А, либо В"] - тоже формулы.
Никаких других формул, кроме указанных в языке логики высказываний нет.
Заглавные латинские буквы А и В, которые употребляются в определении формулы, принадлежат метаязыку и называются метабуквами.
Содержащие метабуквы выражения (А\/В), (А/\В), (А→В), (А↔В) - не формулы, а схемы формул определенного вида.
Относительно любой последовательности знаков алфавита языка логики высказываний можно решить, является она формулой.
Если она построена в соответствии с указанными правилами, то она - формула, если нет, обычная последовательность знаков.

Формула логики высказываний.







Определение формулы логики высказываний: - пропозициональная переменная есть формула; - если А произвольная формула, то

Слайд 13 Точный смысл (семантика) логических знаков может быть разъяснен с помощью

специальных таблиц, в которых зафиксировано, при каких логических значениях формул

А, В формулы , (А/\В), (A\/B), (А→В), (А↔В) и (А В) истинны, а при каких ложны.

Семантика логических знаков.







Точный смысл (семантика) логических знаков может быть разъяснен с помощью специальных таблиц, в которых зафиксировано, при каких

Слайд 14 Рассмотрим таблицы формул, содержащих в качестве главного логического знака различные

логические союзы. Отрицание






Семантическая таблица отрицания.






Рассмотрим таблицы формул, содержащих в качестве главного логического знака различные логические союзы. Отрицание Семантическая таблица отрицания.

Слайд 15








Так как каждая из формул А и В может быть

истинной или ложной, то возможны четыре различных случая: А и

В обе истинны; А ложна, а В истинна; А истинна, но В ложна; наконец, А и В обе ложны. Таблица построена таким образом, что в первых двух столбцах каждая строка - это одно из возможных сочетаний логических значений А и В. Для каждого из них в соответствующей строке третьего столбца указано логическое значение (А/\В). Из таблицы видно, что формула (А/\В) истинна в случае, когда формулы А и В истинны, и ложна в остальных.

Семантическая таблица отрицания.







Так как каждая из формул А и В может быть истинной или ложной, то возможны четыре различных

Слайд 16








Формула А\/В истинна тогда и только тогда, когда истинна по

крайней мере одна из формул А и В.
Семантическая таблица

отрицания.







Формула А\/В истинна тогда и только тогда, когда истинна по крайней мере одна из формул А и

Слайд 17



Формула (А -› В) ложна тогда и только тогда, когда

формула А истинна, а В ложна, и истинна, если формула

А ложна или если формула В истинна.

Семантическая таблица отрицания.







Формула (А -› В) ложна тогда и только тогда, когда формула А истинна, а В ложна, и

Слайд 18






Формула (А ↔ В) истинна либо когда формулы А и

В обе истинны, либо когда они обе ложны.
Семантическая таблица

отрицания.







Формула (А ↔ В) истинна либо когда формулы А и В обе истинны, либо когда они обе

Слайд 19








Формула (А В) истинна, когда А ложно, но В

истинно, или когда А истинно, но В - ложно. В

остальных случаях она - ложна.

Семантическая таблица исключающей (строгой) дизъюнкции.







Формула (А В) истинна, когда А ложно, но В истинно, или когда А истинно, но В

Слайд 20 Перевод формул к логическим союзам «и», «не», «или» .
1. Нужно

выявить все элементарные высказывания, которые входят в состав данного сложного,

и различным элементарным высказываниям поставить в соответствие различные пропозициональные переменные.
2. Нужно определить логические постоянные, с помощью которых построено данное сложное высказывание. Союз о имеет здесь, очевидно, тот же смысл, какой имеет союз и, поэтому переведем его знаком конъюнкции Л. Первое или можно перевести знаком дизъюнкции V. Второе или скорее всего имеет смысл строгой дизъюнкции.
3. Анализируя порядок, в котором данное сложное высказывание строится из элементарных, нужно написать соответствующую ему формулу.
Осуществив настоящий перевод с естественного языка на язык логики высказываний, мы достигли того, что избавились от всей информации, которая не относится к логике, выявили логическую структуру сложного высказывания, сделали ее недвусмысленной и доступной прямому наблюдению.







Семантическая таблица исключающей (строгой) дизъюнкции.

Перевод формул к логическим союзам «и», «не», «или» . 1. Нужно выявить все элементарные высказывания, которые входят в

Слайд 21Исчисление истинностных значений логических формул. Тождественно-истинные и тождественно-ложные формулы.
Введение: Исчисление

истинностных значений логических формул.
Тема 1: Порядок логических действий.
Тема 2: Тождественно

- Истинные и Тождественно - Ложные формулы.

Тема 3: Понятие тождественно-истинной формулы. Некоторые свойства тождественно-истинных формул.

Тема 4: Понятие тождественно-ложной формулы.

Модуль 2.







Исчисление истинностных значений логических формул. Тождественно-истинные и тождественно-ложные формулы.Введение: Исчисление истинностных значений логических формул.Тема 1: Порядок

Слайд 22 Исчисление истинностных значений логических формул осуществляется с помощью семантических таблиц

для соответствующих логических союзов.

Исчисление истинностных значений логических формул.






Исчисление истинностных значений логических формул осуществляется с помощью семантических таблиц для соответствующих логических союзов. Исчисление истинностных значений логических

Слайд 23 Вычисление логического значения формулы по заданным логическим значениям ее переменных

удобно проводить следующим образом. Выпишем формулу в одну строку и

под пропозициональными переменными напишем их логические значения, затем в соответствии с шагами построения формулы под каждым логическим знаком выписываем логическое значение подформулы, в которой этот знак является главным. Логическое значение формулы будет написано под ее главным логическим знаком.
По каждой формуле логики высказываний всегда можно построить отвечающую ей таблицу, в которой зафиксировано, какие логические значения будет получать данная формула при различных наборах логических значений своих переменных.
Если n - число входных столбцов, то число строк, содержащих все различные наборы логических значений n переменных, равно 2 в степени n.

Порядок логических действий.







Вычисление логического значения формулы по заданным логическим значениям ее переменных удобно проводить следующим образом. Выпишем формулу в

Слайд 24 Существуют формулы, которые при любых наборах логических значений переменных получают

в заключительном столбце таблицы логическое значение "истина". Такие формулы называют

тождественно-истинными формулами, или логическими тождествами.
Рассмотрим, формулу p→p и построим ее таблицу:
Таблица




Построим теперь для формулы р V ~ р ее таблицу:
Таблица




Мы видим, что независимо от того, принимает переменная р значения "истина" или "ложь", формула р V ~ р имеет значение "истина".

Тождественно - Истинные и Тождественно - Ложные формулы.







Существуют формулы, которые при любых наборах логических значений переменных получают в заключительном столбце таблицы логическое значение

Слайд 25 Каждая тождественно-истинная формула выражает логический закон. Формула p->р есть известный

логический закон тождества, а формула р V ~ р -

закон исключенного третьего.











Понятие тождественно-истинной формулы. Некоторые свойства тождественно-истинных формул.







Каждая тождественно-истинная формула выражает логический закон. Формула p->р есть известный логический закон тождества, а формула р V

Слайд 26

Таким образом, существуют формулы, которые истинны при любых логических значениях

своих переменных.
Некоторые свойства тождественно-истинных формул:
- Если формулы А→В и

В→С - тождественно-истинны, то формула А→С - тождественно истинная формула
- Формула А равносильна формуле В тогда и только тогда, когда формула А↔В тождественно-истинная формула.







Понятие тождественно-истинной формулы. Некоторые свойства тождественно-истинных формул.

Таким образом, существуют формулы, которые истинны при любых логических значениях своих переменных. Некоторые свойства тождественно-истинных формул: - Если

Слайд 27 Существуют также формулы, которые при любых наборах логических значений переменных

получают в заключительном столбце своей таблицы логическое значение "ложь". Они

называются тождественно-ложными (противоречивыми) формулами.
Рассмотрим, формулу р & ~р, которая имеет следующую таблицу:
Таблица




Рассмотрим далее формулу: р ↔ ~р, которая имеют следующую таблицу:
Таблица

Понятие тождественно-ложной формулы.







Существуют также формулы, которые при любых наборах логических значений переменных получают в заключительном столбце своей таблицы логическое

Слайд 28Двойственность логических формул. Равносильные формулы.
Введение: Двойственность логических формул. Равносильные формулы.
Тема

1: Закон двойственности.
Тема 2: Понятие самодвойственной формулы.
Тема 3: Равносильные формулы.
Тема

4: Свойства равносильности.

Модуль 3.







Двойственность логических формул. Равносильные формулы.Введение: Двойственность логических формул. Равносильные формулы.Тема 1: Закон двойственности.Тема 2: Понятие самодвойственной формулы.Тема

Слайд 29 Знаки ↔ и - являются двойственными знаками.
Определение


Пусть А формула, в которую не входит знак →. Формулой,

двойственной А, называют формулу А*, которая получается из А заменой каждого вхождения знаков
/\ соответственно двойственными им знаками \/.
Если формула А* двойственна формуле А, то и, наоборот, формула А двойственна формуле А*.
Рассмотрим таблицы для конъюнкции и дизъюнкции. Можно видеть, что если в таблице для конъюнкции во всех трех столбцах для А, В и (А/\В) все логические значения "истина" заменить логическими значениями "ложь", а все логические значения "ложь" - логическими значениями "истина", то получим таблицу формулы (А\/В). Если же в таблице формулы (А\/В) аналогичным образом во всех трех столбцах для А, В поменять все логические значения на противоположные, то получим таблицу формулы (А/\В). Эти соотношения находят выражение в равносильностях .

Двойственность логических формул. Равносильные формулы.







Знаки ↔ и - являются двойственными знаками. Определение Пусть А формула, в которую не входит

Слайд 30 То же самое имеет место в отношении таблиц для эквивалентности

и строгой дизъюнкции; таблица формулы (А↔В) переходит при взаимной замене

логических значений во всех трех столбцах в таблицу формулы (A В), а таблица формулы (А В) - в таблицу формулы (А↔В). Эти соотношения находят выражение в равносильностях .
Можно видеть также, что таблица для отрицания при подобной замене переходит в саму себя.

Двойственность логических формул. Равносильные формулы.







То же самое имеет место в отношении таблиц для эквивалентности и строгой дизъюнкции; таблица формулы (А↔В) переходит

Слайд 31 Если А* и В* - формулы, двойственные соответственно формулам А

и В и если А равносильно В, то А* равносильно

В*.

Закон двойственности.







Если А* и В* - формулы, двойственные соответственно формулам А и В и если А равносильно В,

Слайд 32 Определение : Формула А называется самодвойственной, если А равносильно А*.


Определение : Формула А называется несамодвойственной, если в ее таблице

имеются хотя бы два набора логических значений переменных, получающихся друг из друга заменой каждого логического значения на противоположное, для которых А получает в заключительном столбце одно и то же логическое значение.

Понятие самодвойственной формулы.







Определение : Формула А называется самодвойственной, если А равносильно А*. Определение : Формула А называется несамодвойственной, если

Слайд 33 Иногда различные по своей структуре формулы таковы, что одинаковым наборам

логических значений переменных во входных столбцах таблиц этих формул отвечают

одинаковые логические значения в соответствующих строках заключительных столбцов.

Одинаковым набором логических знаний переменных р и q во входных столбцах отвечают одинаковые логические значения в соответствующих строках заключительных столбцов. О подобных формулах говорят, что они равносильны.

Определение Пусть А и В - формулы, E1 , E2, .... En список всех пропозициональных переменных, входящих по крайней мере в одну из них. Будем говорить, что А и В - равносильные формулы (и писать: А равносильно В), если при любых логических значениях E1 E2, ..., En логические значения А и В совпадают.
Равносильными, следовательно, могут быть не только такие формулы, в которые входят одни и те же пропозициональные переменные, но и такие, в которые входят разные переменные.

Равносильные формулы.







Иногда различные по своей структуре формулы таковы, что одинаковым наборам логических значений переменных во входных столбцах таблиц

Слайд 34 Отношение равносильности имеет следующие свойства:
во-первых, рефлексивно, т. е. А равносильно

А;
во-вторых, симметрично, т. е. если А равносильно В, то

В равносильно А;
в-третьих, транзитивно, т. е. если А равносильно В и В равносильно С, то А равносильно С.

Два высказывания называются равнозначными, если они могут быть получены из равносильных формул А и В в результате замены всех входящих в них переменных конкретными высказываниями.

Некоторые равносильные формулы
равносильно А
Пусть А, В, С любые формулы, тогда
А/\В равносильно В/\А А/\(В/\С) равносильно (А/\В)/\С
Равносильности (2) и (3) свидетельствуют о коммутативности и ассоциативности конъюнкции.

Свойства равносильности.







Отношение равносильности имеет следующие свойства:во-первых, рефлексивно, т. е. А равносильно А; во-вторых, симметрично, т. е. если А

Слайд 35А\/В равносильно В\/А; А\/(В\/С) равносильно (А\/В)\/С
Данные равносильности свидетельствуют о

коммутативности и ассоциативности дизъюнкции.
А\/(В/\С) равносильно (А/\В)\/(А/\С)
(В/\С)\/А равносильно (А/\В)\/(А/\С)
А/\(В\/С)

равносильно (А\/В)/\(А\/С)
(В\/С)/\А равносильно (А\/В)/\(А\/С)

Свойства равносильности.







А\/В равносильно В\/А; А\/(В\/С) равносильно (А\/В)\/С Данные равносильности свидетельствуют о коммутативности и ассоциативности дизъюнкции.А\/(В/\С) равносильно (А/\В)\/(А/\С)

Слайд 36 Данные равносильности свидетельствуют о дистрибутивности дизъюнкции относительно конъюнкции и дистрибутивности

конъюнкции относительно дизъюнкции.
А/\А равносильно А
А\/А равносильно А
Указанные равносильности

называются законами идемпотентности конъюнкции и дизъюнкции.
~ (А/\В) равносильно ~ /\ ~
~ (А\/В) равносильно ~ \/ ~
Данные равносильности называются законами де Моргана.
А\/В равносильно ~ (А → )
A → B равносильно ~ /\B

Свойства равносильности.







Данные равносильности свидетельствуют о дистрибутивности дизъюнкции относительно конъюнкции и дистрибутивности конъюнкции относительно дизъюнкции.А/\А равносильно А А\/А равносильно

Слайд 37~ И равносильно Л
~ Л равносильно И
А↔И равносильно

А
А↔Л равносильно
А/\И равносильно А
И/\А равносильно А


А/\Л равносильно Л
Л/\А равносильно Л
А\/И равносильно И
И\/А равносильно И
Л\/А равносильно А
Л\/А равносильно А

Свойства равносильности.







~ И равносильно Л ~ Л равносильно И А↔И равносильно А А↔Л равносильно А/\И равносильно А

Слайд 38Понятие нормальной формы.
Введение: Понятие нормальной формы.
Тема 1: Процедура приведения к

нормальной форме.
Тема 2: Проблема разрешимости.
Тема 3: Конъюнктивная нормальная, совершенная и

сокращенная форма.

Тема 4: Дизъюнктивная нормальная, совершенная и сокращенная форма.

Модуль 4.







Понятие нормальной формы.Введение: Понятие нормальной формы.Тема 1: Процедура приведения к нормальной форме.Тема 2: Проблема разрешимости.Тема 3: Конъюнктивная

Слайд 39 Определение : Формула логики высказываний имеет нормальную форму, если она:

а) не содержит знаков , ↔ и

б) знаки отрицания стоят в ней только при переменных.

Понятие нормальной формы.







Определение : Формула логики высказываний имеет нормальную форму, если она: а) не содержит знаков , ↔ и

Слайд 40 Любую формулу А, не имеющую нормальной формы, можно конечным числом

применений правила замены преобразовать в формулу А', которая имеет нормальную

форму. Процесс такого преобразования будем называть процессом приведения формулы к нормальной форме.
Для того чтобы данную формулу привести к нормальной форме, необходимо произвести в ней следующие равносильные замены:
каждую подформулу вида (А В) заменить согласно равносильности формулой ((А V В) & (~ А V ~ В));
каждую подформулу вида (А В) заменить согласно равносильности формулой ((~AVB)&(~BV A));
каждую подформулу вида (А→В) заменить согласно равносильности формулой (~А V В);
каждую подформулу вида ~ (А & В) заменить согласно равносильности формулой (~А V ~В);
каждую подформулу вида ~ (А V В) заменить согласно равносильности формулой (~А & ~В);
каждую подформулу вида ~ ~А заменить согласно равносильности формулой А.
Формула имеет нормальную форму, если ни один из перечисленных пунктов настоящего предписания к ней не применим.

Процедура приведения к нормальной форме.







Любую формулу А, не имеющую нормальной формы, можно конечным числом применений правила замены преобразовать в формулу А',

Слайд 41 Каждая формула логики высказываний принадлежит к одному из трех следующих

классов:
истинная при всех логических значениях своих переменных (тождественно-истинная формула или

общезначимая формула);
ложная при всех логических значениях своих переменных (тождественно-ложная формула, или логическое противоречие, она же невыполнимая формула);
истинная формула при одних логических значениях и ложная при других (иногда истинная формула, или выполнимая формула).
Задача нахождения процедуры, которая позволяет для любой формулы выяснить, к какому из трех указанных классов она принадлежит, называется семантической процедурой разрешения для формул логики высказываний. В соответствии с этим процедура, позволяющая конечным числом простых действий решить проблему разрешения, называется разрешающей процедурой. Заметим, что для того чтобы получить разрешающую процедуру, достаточно найти способ, позволяющий отличить тождественно-истинные формулы от всех остальных. В самом деле, если в результате применения такой процедуры к формуле А выясняется, что она тождественно-истинна, то проблема разрешения решена. Если же выясняется, что она не тождественно-истинна, то данную процедуру нужно применить к формуле ~ А.

Проблема разрешимости.







Каждая формула логики высказываний принадлежит к одному из трех следующих классов:истинная при всех логических значениях своих переменных

Слайд 42 Если в результате ее применения к формуле ~ А, выяснится,

что ~ А тождественно-истинная формула, то значит, формула А тождественно-ложна.

Если же ~ А так же как А не тождественно-истинна, - значит, формула А выполнимая, т. е. при одних значениях переменных она истинна, а при других ложна. Некоторая пропозициональная переменная входит в формулу, приведенную к нормальной форме, регулярно, если она входит в нее одновременно с отрицанием и без отрицания. Если переменная входит в формулу, приведенную к нормальной форме, только с отрицанием или только без отрицания, то будем говорить, что она входит в формулу нерегулярно.

Проблема разрешимости.







Если в результате ее применения к формуле ~ А, выяснится, что ~ А тождественно-истинная формула, то значит,

Слайд 43 Разрешающая процедура заключается в:
приводим формулу к нормальной форме;
в формуле,

приведенной к нормальной форме, выделяем переменные, которые входят в нее

нерегулярно;
вместо всех нерегулярно входящих переменных и отрицаний нерегулярно входящих переменных подставляем на всех местах, где они встречаются в нормальной форме, букву Л, т. е. подставляем Л вместо переменной или вместо отрицания переменной;
применяем правило замены по равносильностям ко всем подформулам получившейся формулы до тех пор, пока остаются поводы для его применения. В результате длина формулы будет сокращаться и могут понадобиться новые нерегулярно входящие переменные. С ними поступаем таким же образом, т. е. согласно пунктам 3) и 4). Предусмотренные в пунктах. 2) - 4) преобразования повторяем до тех пор, пока не получим формулу, не содержащую нерегулярно входящих переменных;
рассматриваем следующие две формулы, которые получаются из формулы, не содержащей нерегулярно входящих переменных, если:
вместо одной из регулярно входящих переменных на всех местах подставить букву И и применить правило равносильной замены согласно равносильностям;
вместо той же самой переменной на всех местах подставить букву Л и применить правило равносильной замены согласно равносильностям.

Проблема разрешимости.







Разрешающая процедура заключается в:приводим формулу к нормальной форме; в формуле, приведенной к нормальной форме, выделяем переменные, которые

Слайд 44 К формулам а) и б), если это возможно, снова применяем

пункты 2) - 4), а затем из формул а) и

б) получаем соответственно формулы аа), аб) и ба), бб) и т. д. до тех пор, пока не исчерпаем возможности применения пунктов 2) - 5).
Если в результате применения данной процедуры к произвольной формуле А все заключительные формулы будут И, те формула А тождественно-истинная, если же хотя бы одна заключительная формула есть Л, то формула А не тождественно-истинная.

Проблема разрешимости.







К формулам а) и б), если это возможно, снова применяем пункты 2) - 4), а затем из

Слайд 45 Укажем простой метод, позволяющий по виду формулы, приведенной к некоторой

стандартной форме, судить о том, тождественно-истинна она или нет.
Условимся называть

элементарной дизъюнкцией формулу, которая имеет вид
Al V A2 V...An.
Наличие переменной и ее отрицания не только достаточное, но и необходимое условие тождественной истинности элементарной дизъюнкции.
Определение Формула логики высказываний имеет конъюнктивную нормальную форму (КНФ), если она имеет вид
В1&В2&...&Вn
где Bl, B2, ..., Вn- элементарные дизъюнкции.
Любая формула логики высказываний в результате ряда равносильных замен может быть приведена к конъюнктивной нормальной форме. Формулу, равносильную данной и имеющую конъюнктивную нормальную форму, будем называть конъюнктивной нормальной формой данной формулы.

Конъюнктивная нормальная, совершенная и сокращенная форма.







Укажем простой метод, позволяющий по виду формулы, приведенной к некоторой стандартной форме, судить о том, тождественно-истинна она

Слайд 46 Для того чтобы формулу привести к КНФ, необходимо вначале с

помощью известной процедуры привести ее к нормальной форме. Затем каждую

подформулу вида (А & (В V С)) согласно равносильностям в каждую подформулу вида ((В & С) V А) согласно равносильности заменить формулой ((А V В) & (А V С)).
Формула имеет КНФ, если она имеет нормальную форму и в ней нет подформул вида (А V (В & С)) и ((В & С) V А).
Формула, имеющая КНФ, тождественно-истинна тогда и только тогда, когда тождественно-истинны все ее конъюнктивные члены, т. е. когда каждая элементарная дизъюнкция содержит хотя бы одну пару дизъюнктов, из которых один есть некоторая переменная, а другой - ее отрицание.

Конъюнктивная нормальная, совершенная и сокращенная форма.







Для того чтобы формулу привести к КНФ, необходимо вначале с помощью известной процедуры привести ее к нормальной

Слайд 47 Таким образом, по виду некоторой формулы в КНФ можно судить

о том, тождественно-истинна она или нет.
Каждая не тождественно-истинная формула имеет

КНФ, которая называется совершенной.
Определение Совершенной конъюнктивной нормальной формой (СКНФ) некоторой формулы называется такая ее КНФ, которая удовлетворяет следующим условиям:
в ней нет двух одинаковых конъюнктивных членов (одинаковыми считаются такие конъюнктивные члены, которые поучаются один из другого в результате замены по равносильности );
ни в одном конъюнктивном члене нет двух одинаковых дизъюнктов;
ни в одном конъюнктивном члене нет таких двух дизъюнктов, из которых один есть переменная, а другой - отрицание этой переменной;
в каждом конъюнктивном члене содержатся все переменные данной формулы.







Конъюнктивная нормальная, совершенная и сокращенная форма.

Таким образом, по виду некоторой формулы в КНФ можно судить о том, тождественно-истинна она или нет. Каждая не

Слайд 48 Для того чтобы привести формулу к СКНФ, необходимо:
известным уже способом

привести ее к КНФ;
на основании равносильностей устранить из КНФ

повторяющиеся конъюнкты, т. е. из всех имеющихся одинаковых конъюнктивных членов оставить один и вычеркнуть остальные;
на основании равносильностей устранить все повторения в конъюнктивных членах КНФ, т. е. из всех имеющихся одинаковых дизъюнктов оставить один и вычеркнуть остальные;
на основании равносильностей устранить из КНФ те конъюнктивные члены, которые являются тождественно-истинными элементарными дизъюнкциями;
ко всем тем конъюнктивным членам, в которых отсутствует какая-нибудь из содержащихся в данной формуле переменных Е, на основании равносильности приписать знак дизъюнкции и вслед за ним тождественно-ложную конъюнкцию (Е & ~ Е), а затем применить правило замены). Эту процедуру повторять до тех пор, пока не окажется, что в каждый конъюнктивный член входят все переменные, содержащиеся в данной формуле;
если в получившейся КНФ снова появились одинаковые конъюнктивные члены, то надо устранить повторения.







Конъюнктивная нормальная, совершенная и сокращенная форма.

Для того чтобы привести формулу к СКНФ, необходимо:известным уже способом привести ее к КНФ; на основании равносильностей

Слайд 49 Сокращенной КНФ данной формулы называется такая ее КНФ, которая удовлетворяет

следующим условиям:
ни в одном конъюнктивном члене нет двух одинаковых дизъюнктов;


ни в одном конъюнктивном члене нет таких двух дизъюнктов, из которых один есть переменная, а другой отрицание этой переменной;
нет таких пар конъюнктивных членов, что каждый дизъюнкт из одного имеется в другом, т.е., во-первых, нет двух одинаковых конъюнктивных членов, а во-вторых, нет таких двух конъюнктивных членов, из которых один поглощается другим;
если имеются такие два конъюнктивных члена, из которых один содержит некоторую переменную, а другой - ее отрицание (при условии, что другой переменной, для которой это же имеет место, в данных конъюнктах нет), то в той же КНФ имеется конъюнктивный член, который является элементарной дизъюнкцией, построенной из всех дизъюнктов данной пары, отличных от упомянутой переменной и ее отрицания.







Конъюнктивная нормальная, совершенная и сокращенная форма.

Сокращенной КНФ данной формулы называется такая ее КНФ, которая удовлетворяет следующим условиям:ни в одном конъюнктивном члене нет

Слайд 50 Для того чтобы привести формулу к сокращенной КНФ, нужно:
привести ее

к КНФ;
из всех одинаковых конъюнктивных членов КНФ оставить только

один и в элементарных дизъюнкциях также устранить все повторения;
устранить из КНФ все тождественно-истинные конъюнктивные члены;
если среди конъюнктивных членов КНФ имеются два таких, что один содержит некоторую переменную, а другой - ее отрицание, то на основании закона выявления, добавить новый конъюнктивный член, представляющий собой дизъюнкцию остальных дизъюнктов этих двух конъюнктивных членов, но лишь при условии, что новый конъюнктивный член не тождественно-истинный и отличается от уже имеющихся.







Конъюнктивная нормальная, совершенная и сокращенная форма.

Для того чтобы привести формулу к сокращенной КНФ, нужно:привести ее к КНФ; из всех одинаковых конъюнктивных членов

Слайд 51 Формулы логики высказываний наряду с КНФ могут иметь дизъюнктивную нормальную

форму (ДНФ).
Условимся называть элементарной конъюнкцией формулу, которая имеет вид
А1&А2&...&АП.
Наличие переменной

и ее отрицания не только достаточное, но и необходимое условие тождественной ложности элементарной конъюнкции.
Определение Формула логики высказываний имеет дизъюнктивную нормальную форму, если она имеет вид
В1 V В2 V ... V Вп.
Любая формула логики высказываний в результате ряда равносильных замен может быть приведена к дизъюнктивной нормальной форме. Формулу, равносильную данной и имеющую дизъюнктивную нормальную форму, будем называть дизъюнктивной нормальной формой данной формулы.
Формула не единственным образом представима в ДНФ. Формула, имеющая ДНФ, тождественно-ложна тогда и только тогда, когда тождественно-ложны все ее дизъюнктивные члены, т. е. когда каждая элементарная конъюнкция содержит хотя бы одну пару конъюнктов, из которых один есть некоторая переменная, а другой - ее отрицание. Каждая не тождественно-ложная формула имеет ДНФ, которая называется совершенной.

Дизъюнктивная нормальная, совершенная и сокращенная форма.







Формулы логики высказываний наряду с КНФ могут иметь дизъюнктивную нормальную форму (ДНФ). Условимся называть элементарной конъюнкцией формулу, которая

Слайд 52 Определение Совершенной дизъюнктивной нормальной формой (СДНФ) некоторой формулы называется такая

ее ДНФ, которая удовлетворяет следующим условиям:
в ней нет двух

одинаковых дизъюнктивных членов (одинаковыми считаются такие дизъюнктивные члены, которые получаются один из другого в результате замены );
ни в одном дизъюнктивном члене нет двух одинаковых конъюнктов;
ни в одном дизъюнктивном члене нет таких двух конъюнктов, из которых один есть переменная, а другой - отрицание этой переменной;
в каждом дизъюнктивном члене содержатся все переменные данной формулы.
Для того чтобы привести формулу к СНДФ, необходимо:
привести ее к ДНФ;
на основании равносильностей устранить из ДНФ повторяющиеся дизъюнкты, т. е. из всех имеющихся одинаковых дизъюнктов оставить один и вычеркнуть остальные;
на основании равносильностей устранить все повторения в дизъюнктивных членах ДНФ, т. е. из всех имеющихся одинаковых конъюнктов оставить один и вычеркнуть остальные;
на основании равносильностей устранить из формулы тe дизъюнктивные члены, которые являются тождественно-ложными элементарными конъюнкциями;







Дизъюнктивная нормальная, совершенная и сокращенная форма.

Определение Совершенной дизъюнктивной нормальной формой (СДНФ) некоторой формулы называется такая ее ДНФ, которая удовлетворяет следующим условиям: в

Слайд 53всем тем дизъюнктивным членам, в которых отсутствует какая-нибудь из содержащихся

в данной формуле переменных Е, на основании равносильностей приписать знак

конъюнкции, вслед за ним - тождественно-истинную дизъюнкций (Е V ~Е) и применить правило замены . Эту процедуру повторять до тех пор, пока не окажется, что в каждый дизъюнктивный член входят все переменные, содержащиеся в данной формуле;
если в получившейся ДНФ снова появились одинаковые дизъюнктивные члены, то надо устранить повторения.







Дизъюнктивная нормальная, совершенная и сокращенная форма.

всем тем дизъюнктивным членам, в которых отсутствует какая-нибудь из содержащихся в данной формуле переменных Е, на основании

Слайд 54 Определение Сокращенной ДНФ данной формулы называется такая ее ДНФ, которая

удовлетворяет следующим условиям:
ни в одном дизъюнктивном члене нет двух

одинаковых конъюнктов;
ни в одном дизъюнктивном члене нет таких двух конъюнктов, из которых один есть переменная, а другой - отрицание этой переменной;
нет таких пар дизъюнктивных членов, что каждый конъюнкт из одного имеется в другом, т. е., во-первых, нет двух одинаковых дизъюнктивных членов, а во-вторых, нет таких двух дизъюнктивных членов, из которых один поглощается другим;
если имеются такие два дизъюнктивных члена, из которых один содержит некоторую переменную, а другой - ее отрицание (при условии, что другой переменной, для которой это же имеет место, в данных дизъюнктах нет), то в этой же ДНФ имеется дизъюнктивный член, который является элементарной конъюнкцией, построенной из всех конъюнктов данной пары, отличных от упомянутой переменной и ее отрицания.
Для того чтобы привести формулу к сокращенной ДНФ, нужно произвести следующие преобразования;
привести ее к ДНФ;
из всех одинаковых дизъюнктивных членов ДНФ оставить только один и в элементарных конъюнкциях тоже устранить все повторения;
устранить из ДНФ все тождественно-ложные дизъюнктивные члены;







Дизъюнктивная нормальная, совершенная и сокращенная форма.

Определение Сокращенной ДНФ данной формулы называется такая ее ДНФ, которая удовлетворяет следующим условиям: ни в одном дизъюнктивном

Слайд 55если среди дизъюнктивных членов ДНФ имеются два таких, что один

содержит некоторую переменную, а другой - ее отрицание, то на

основании закона выявления, добавить новый дизъюнктивный член, представляющий собой конъюнкцию остальных конъюнктов этих двух дизъюнктивных членов, но лишь при условии, что новый дизъюнктивный член не тождественно-ложный и отличается от всех уже имеющихся;
если в новых дизъюнктивных членах ДНФ имеются повторения, то устранить их;
если среди дизъюнктивных членов ДНФ имеются такие, которые поглощаются другими, то, применяя правило замены , устранить все поглощаемые дизъюнктивные члены.
Получившаяся в результате формула есть сокращенная ДНФ данной формулы, каждый дизъюнкт которой - ее простая гипотеза.
Таким образом, для того чтобы получить все простые гипотезы, т. е. найти те самые слабые допущения, при которых данная формула была бы их следствием, нужно привести формулу к сокращенной ДНФ.







Дизъюнктивная нормальная, совершенная и сокращенная форма.

если среди дизъюнктивных членов ДНФ имеются два таких, что один содержит некоторую переменную, а другой - ее

Слайд 56Логическое следование. Естественный вывод в логике высказываний.
Введение: Логическое следование.
Тема 1:

Понятие логического вывода.
Тема 2: Правила вывода.
Тема 3: Правило построения

прямого доказательства.

Тема 4: Косвенное доказательство.

Тема 5: Сильное (классическое) косвенное доказательство.

Тема 6: Аксиоматическое представление логики высказываний.

Тема 7: Полнота классического исчисления высказываний.

Тема 8: Построение доказательств в логике высказываний.

Модуль 5.







Логическое следование. Естественный вывод в логике высказываний.Введение: Логическое следование.Тема 1: Понятие логического вывода. Тема 2: Правила вывода.Тема

Слайд 57 Пусть A1, A2. ..., An и В - формулы, a

-E1, E2, ..., Em - совокупность всех пропозициональных переменных, входящих

по крайней мере в одну из них. Будем говорить, что формула В логически следует из формул А1, А2,..., An, если при всех тех логических значениях E1, E2, ..., Em, при которых формулы A1, A2, ..., An истинны, она тоже истинна.

Логическое следование.







Пусть A1, A2. ..., An и В - формулы, a -E1, E2, ..., Em - совокупность всех

Слайд 58 Формула В называется в этом случае логическим следствием (заключением) формул

A1, A2, ..., An, а формулы A1, A2, ..., An

называются посылками формулы В.
Используя в качестве разрешающей процедуры процесс приведения формул к КНФ, можно для любой формулы В и любого списка формул A1, A2, ..., An, решить логическую задачу: является В логическим следствием совокупности посылок A1, A2, ... An, или нет.
Метод систематического обзора следствий из любого числа посылок.
Связываем посылки знаком конъюнкции, и получившуюся формулу приводим к СКНФ. Каждый конъюнктивный член СКНФ, а также любая конъюнкция конъюнктивных членов являются следствием конъюнкции посылок,
╞ Q, е! ╞ Р→Q
Р1,Р2, ...,Рn-1,Рn ╞ Q,e!
╞ (Р1→(Р2→...→(Pn-1 (Pn Q)))).

Логическое следование.







Формула В называется в этом случае логическим следствием (заключением) формул A1, A2, ..., An, а формулы A1,

Слайд 59 Метод сокращенных таблиц - в качестве начального предположения будет выступать

то, что искомое высказывание не является общезначимым, Исходя из такого

предположения, на основании таблиц истинности определяют значения истинности пропозициональных букв (простых высказываний).

Логическое следование.







Метод сокращенных таблиц - в качестве начального предположения будет выступать то, что искомое высказывание не является общезначимым,

Слайд 60 Как формы выражения логических законов, тождественно-истинные формулы, или логические тождества,

используются для обоснования правил логического следования. С точки зрения самой

процедуры их обоснования особое значение имеет способ представления формул в виде так называемых кратных импликаций.
Кратной импликацией называется формула вида
A1→(A2→...(An→C).
Формула читается так: если A1, A2, ..., An, то С. Члены кратной импликации, обозначенные в данной формуле посредством A1, A2, ... , An, называются антецедентами, а член С - консеквентом.
При n = 1 имеем схему однократной (обычной) импликации
A1→C ;
при n = 2 - схему двукратной импликации
A1→(A2 →С) ;
при n = 3 - схему трехкратной импликации
A1→(A2→(A3→С)) и т. д.

Понятие логического вывода.







Как формы выражения логических законов, тождественно-истинные формулы, или логические тождества, используются для обоснования правил логического следования. С

Слайд 61 При n = О считаем, что формула, построенная по данной

схеме кратной импликации, совпадает с формулой С. В этом случае

мы имеем дело с так называемой нулькратной, или, как еще говорят, "вырожденной" импликацией. Любую формулу, независимо от того, содержит она знак импликации в качестве главного логического знака или нет, можно рассматривать как кратную импликацию.

Понятие логического вывода.







При n = О считаем, что формула, построенная по данной схеме кратной импликации, совпадает с формулой С.

Слайд 62 В логике правила следования записываются в виде фигур рассуждения
A1, ...

A2, ..., An С
которые читаются так: из A1, A2, ... ,

An следует (или выводится) С. Члены A1 , A2, . . . , An называются посылками, а член С называется заключением данной фигуры. Но, конечно, не всякая фигура такого вида является правилом следования. Определение правила логического следования.
Фигура
A1, A2, ... , An С
называется корректной фигурой, или правилом следования, если формула вида
A1 (A2 ... (An C)...)
есть логическое тождество.

Правила вывода.







В логике правила следования записываются в виде фигур рассужденияA1, ... A2, ..., An С которые читаются так: из

Слайд 63 Таким образом, для проверки корректности некоторой фигуры рассуждения нужно образовать

кратную импликацию, сделав посылки фигуры а заключение фигуры - консеквентом

этой импликации, и выяснить, является ли полученная этим путем формула тождественно-истинной.
Процедура ее проверки на тождественную истинность состоит в следующем.
Рассматриваем только те строки таблицы, где под каждым антецедентом стоит символ логического значения "истинно". Тогда:
1) если во всех рассматриваемых строках под консеквентом будет написан также символ логического значения "истинно", то кратная импликация является логическим тождеством и (по определению) соответствующая ей фигура корректна, т. е. представляет правило логического следования;
2) если же среди рассматриваемых строк найдется хотя бы одна, в которой под консеквентом стоит символ логического значения "ложно", то кратная импликация не есть логическое тождество, а соответствующая ей фигура некорректна.

Правила вывода.







Таким образом, для проверки корректности некоторой фигуры рассуждения нужно образовать кратную импликацию, сделав посылки фигуры а заключение

Слайд 64 Логический вывод обозначается следующим знаком: " ├ ".
Формула следующего вида:


P1,P2,.....,Pn ├ Q,
означает, что формула Q выводится из формул P1,

P2, ..., Pn. Такими фигурами выводы являются следующие:МП (modus ponens) А А->В В
Данную фигуру называют также "правилом отделения".
ВК (введение конъюнкции) А В A&В УК (удаление конъюнкции)  A & B A & B
A ; B ВД A B
A V B ; A V B
УД A V A A->C B->C C
УМ (modus tollens) A->B ~ B A-> ~ B B
~ A ; ~ A
Правило ВК означает, что конъюнкция следует из любых двух формул и называется введением конъюнкции.

Правила вывода.







В В Данную фигуру называют также "правилом отделения". ВК (введение конъюнкции) А В A&В УК (удаление конъюнкции)  A & B A & B A ; B ВД A B A V B ; A V B УД A V A A->C B->C C УМ (modus tollens) A->B ~ B A-> ~ B B ~ A ; ~ A Правило ВК означает, что конъюнкция следует из любых двух формул и называется введением конъюнкции.Правила вывода. ">Логический вывод обозначается следующим знаком:

Слайд 65 Правило ВД, состоящее из двух фигур, означает, что дизъюнкция следует

из формулы, совпадающей с одним из ее членов (дизъюнктов), и

называется введением дизъюнкции.
Правило УК, также состоящее из двух фигур, означает, что из конъюнкции следует формула, совпадающая с одним из ее членов (конъюнктов), и называется правилом удаления конъюнкции.
Правило УД называется правилом удаления дизъюнкции и означает, что из двух импликаций, консеквенты которых одинаковы, и дизъюнкции формул, совпадающих с антецедентами этих импликаций, следует формула, совпадающая с консеквентом импликаций.

Правила вывода.







Правило ВД, состоящее из двух фигур, означает, что дизъюнкция следует из формулы, совпадающей с одним из ее

Слайд 66 Применяя правила следования, мы можем из исходных формул, называемых посылками,

или допущениями, получать (выводить) новые формулы, логически следующие из исходных,

путем построения последовательностей формул, в которых каждая формула или является посылкой, или же следует из предшествующих формул по одному из правил следования.
Такого рода последовательности формул называются формальными выводами.

Правила вывода.







Применяя правила следования, мы можем из исходных формул, называемых посылками, или допущениями, получать (выводить) новые формулы, логически

Слайд 67 Прямое доказательство формулы (кратной импликации) вида
A1->(A2->...(An->C)...)
строится:
1. На

любом шаге построения можно написать: одну из формул A1, A2,

... An в качестве допущения;
2. Формулу, следующую из ранее написанных формул по одному из правил логического следования; ранее доказанную формулу.
3. Прямое доказательство формулы считается построенным, если получена последовательность, оканчивающаяся формулой С.
Прямое доказательство кратной импликации осуществляется через построение вывода консеквента доказываемой формулы из ее антецедентов, вписываемых в качестве допущений путем применения правил следования с использованием, возможно, ранее доказанных формул.

Правило построения прямого доказательства.







Прямое доказательство формулы (кратной импликации) видаA1->(A2->...(An->C)...) строится: 1. На любом шаге построения можно написать: одну из

Слайд 68 Косвенное доказательство формулы строится согласно следующему предписанию.
На любом шаге построения

можно написать:
одну из формул A1, A2, ..., An в качестве

допущения;
формулу, противоречащую формуле С;
формулу, следующую из ранее написанных форм по одному из правил логического следования;
ранее доказанную формулу.
Формула называется доказуемой формулой, или логической теоремой (системы N), если можно построить доказательство данной формулы (по правилам системы N).
Кроме того, мы принимаем следующее определение знака эквивалентности:
А В = df (А→В) & (В→А)
Согласно данному определению, если в формуле имеется вхождение выражения из правой части данного определения, то его можно заменять на вхождение выражения из его левой части (и наоборот). Из определения знака непосредственно следует, что правила
ВЭ A→B     B→A A B
УЭ A B A B A→B ; A→B

Косвенное доказательство.







Косвенное доказательство формулы строится согласно следующему предписанию. На любом шаге построения можно написать:одну из формул A1, A2, ...,

Слайд 69 Слабое косвенное доказательство формулы
A1->(A2-> ... (An->С) ... )
строится согласно следующему

предписанию. На любом шаге построения можно написать:
одну из формул

A1, A2, ..., An в качестве допущения;
формулу С, полученную из С стиранием первого слева знака отрицания, в качестве допущения слабого косвенного доказательства;
формулу, следующую из ранее написанных формул, по одному из правил логического следования;
ранее доказанную формулу.
Слабое косвенное доказательство формулы считается построенным, если в соответствии с пунктами 1)-4) получена последовательность формул, содержащая формулу С, пару противоречащих формул и оканчивающаяся одной из формул данной пары.
Слабое косвенное доказательство - это частный случай косвенного доказательства, характеризующийся следующими ограничительными условиями:
если при построении косвенного доказательства мы могли вводить формулу, получаемую из консеквента его тезиса как стиранием, так и приписыванием слева знака отрицания, то в слабом косвенном доказательстве мы располагаем только первой возможностью (стиранием знака отрицания);

Косвенное доказательство.







Слабое косвенное доказательство формулыA1->(A2-> ... (An->С) ... ) строится согласно следующему предписанию. На любом шаге построения можно написать:

Слайд 70если для окончания косвенного доказательства требуется получение последовательности формул, содержащей

пару противоречащих формул, и не требуется, чтобы в эту последовательность

входило специальное допущение косвенного доказательства, то одним из непременных условий окончания слабого косвенного доказательства является наличие допущения слабого косвенного доказательства.

Косвенное доказательство.







если для окончания косвенного доказательства требуется получение последовательности формул, содержащей пару противоречащих формул, и не требуется, чтобы

Слайд 71 Правило построения сильного косвенного доказательства.
Сильное косвенное доказательство формулы
A1->(A2->...(An->C)..)
строится согласно следующему

предписанию. На любом шаге построения можно написать:
одну из формул

A1, A2, ..., An в качестве допущения;
формулу - С в качестве допущения сильного косвенного доказательства;
формулу, следующую из ранее написанных формул, по одному из правил логического следования;
ранее доказанную формулу.
Сильное косвенное доказательство формулы считается построенным, если в соответствии с пунктами 1) - 4), включая и пункт 2), получена последовательность формул, содержащая формулу ~ С, пару противоречащих формул и оканчивающаяся одной из формул данной пары.
Таким образом, выявляется следующая классификация доказательств в системе N. Доказательства подразделяются на прямые и косвенные, а последние в свою очередь делятся на квазисильные и сильные.

Сильное (классическое) косвенное доказательство.







Правило построения сильного косвенного доказательства. Сильное косвенное доказательство формулыA1->(A2->...(An->C)..) строится согласно следующему предписанию. На любом шаге построения можно написать:

Слайд 72 При построении исчисления высказываний гильбертовского типа выбирают конечный запас логических

тождеств или конечный запас эффективно определенных типов логических тождеств в

качестве аксиом и указывают правила, применяя которые можно получать из аксиом новые логические тождества в качестве теорем, или доказуемых формул, соответствующей логической системы.
В описываемой ниже системе Я аксиомами являются формулы следующих видов:
А1. А (В А)
А2. (А (В С)) ((А В) (А С))
A3. А (В (А & В))
А4. (А & В) А
А5. (А & В) В
А6. А (А V В)
А7. В (А V В)
А8. (А С) ((В С) ((А V В) С))
А9. (А В) ((А ~ В) ~ А)
А10. А(~АВ)
А10°. ~ ~А А,

Аксиоматическое представление логики высказываний.







При построении исчисления высказываний гильбертовского типа выбирают конечный запас логических тождеств или конечный запас эффективно определенных типов

Слайд 73 А единственным правилом вывода служит МП. Доказательство в системе Н

формулы F строится согласно следующему предписанию.
На любом шаге построения можно

написать:
одну из аксиом;
формулу, следующую из ранее написанных формул по правилу МП.


Аксиоматическое представление логики высказываний.







А единственным правилом вывода служит МП. Доказательство в системе Н формулы F строится согласно следующему предписанию. На любом

Слайд 74 Доказательство формулы F считается построенным, если в соответствии с пунктами

1) - 2) получена последовательность формул, оканчивающаяся формулой F.
В системе

F формула называется доказуемой формулой или логической теоремой, если можно построить доказательство данной формулы.
Так же как и в системе N, в системе Н вводится по определению.
Рассмотрим пример доказательства формулы вида А→А.
Доказательство.
1.(A→((B→A)→A))→((A→(B→A))→(A→A)) аксиома А2
2.A→((B→A)→A) аксиома А1
3.(A→(B→A))→(A→A)МП (2, 1)4.A→(B→A) аксиома А1
5.A→A МП (4,3) Любое доказательство в системе N можно преобразовать в одноименное доказательство в системе Н.
Системы Н→N эквивалентны.
Если формула F доказуема в системе Н, то F тождественно-истинна.
Любая формула, доказуемая в системе N, тождественно-истинна.

Аксиоматическое представление логики высказываний.







Доказательство формулы F считается построенным, если в соответствии с пунктами 1) - 2) получена последовательность формул, оканчивающаяся

Слайд 75Непротиворечивость логической системы можно определить следующим образом: система называется непротиворечивой,

если в ней недоказуемы некоторая формула и ее отрицание. Иначе

говоря, в непротиворечивой системе не найдется пары формул А и ~ А, из которых каждая доказуема в данной системе.
Для системы, в которой доказуема формула А→(~А→В), сформулированный критерий непротиворечивости эквивалентен следующему: система называется непротиворечивой, если существует хотя бы одна формула, недоказуемая в данной системе. Действительно, если бы в ней можно было найти доказательства каких-то формул А и ~А, то с помощью МП мы на основании данной формулы смогли бы построить доказательство любой формулы В. Заметим, что для логических систем, не содержащих знака отрицания, применяется эта вторая форма критерия непротиворечивости.
Из свойства семантической корректности системы вытекает непротиворечивость данной системы. Действительно, если в логической системе доказуема какая-то пара формул А и ~А, то данная система не является семантически корректной, так как формулы А и ~А, очевидно, не могут быть обе тождественно-истинными. Поэтому если логическая система семантически корректна, то она и непротиворечива.

Аксиоматическое представление логики высказываний.







Непротиворечивость логической системы можно определить следующим образом: система называется непротиворечивой, если в ней недоказуемы некоторая формула и

Слайд 76Логическую систему называют разрешимой теорией, если для нее существует эффективный

метод, позволяющий конечным числом достаточно простых действий для любой формулы

ответить на вопрос, доказуема она или нет в данной системе. Этот эффективный метод называют разрешающей процедурой, или разрешающим алгоритмом.
Из результатов проделанного рассмотрения систем N и H классической логики высказываний следует, что они являются разрешимыми теориями; при этом разрешающей процедурой для них служит табличный метод. Действительно, для любой предъявленной формулы мы в состоянии построить ее таблицу. Если в результате построения таблицы будет установлено, что испытываемая формула тождественно-истинна, то по теореме о полноте она доказуема и можно эффективно построить ее доказательство. Если же окажется, что испытываемая формула не является тождественно-истинной, то по теореме о семантической корректности данная формула не доказуема.
Система H - аксиоматическое представление логики высказываний, так же как и система N естественного вывода,
Для системы H можно доказать теорему, устанавливающую допустимость в ней правила эквивалентной замены. (Формулы А, В называются эквивалентными, если доказуема формула А→В). Согласно этому правилу, если формулы А, В эквивалентны, то, заменив в какой-то формуле F одно или более вхождений А вхождением В, мы получим некоторую формулу G, эквивалентную первоначальной формуле F.







Аксиоматическое представление логики высказываний.

Логическую систему называют разрешимой теорией, если для нее существует эффективный метод, позволяющий конечным числом достаточно простых действий

Слайд 77 Покажем , что система N естественного вывода семантически полна, отложив

установление ее семантической корректности.
Будем говорить, что формула F составлена из

пропозициональных букв E1, E2, ..., En (эти буквы выписаны без повторений), если в перечне E1, E2,..., En имеются все пропорциональные буквы, входящие в F (но могут содержаться и другие, не входящие в F буквы).
Для любой формулы можно указать (неограниченно) много перечней пропозициональных букв, из которых она составлена, но только один из этих перечней будет минимальным, а именно тот, в котором нет пропозициональных букв, не входящих в данную формулу,
Положение 1.
Пусть E1, E2, ...,En - перечень пропозициональных букв, из которых составлена формула F. Тогда, если F есть тождественно-истинная формула, то в системе N доказуема формула
(E1 V ~ E1), (E2 V ~E2), .... (En V ~ En) → F.
Положение 2.
Если формула F тождественно-истинна, то F доказуема в N.
Из положений 1 и 2 следует, что формула F доказуема в N. Доказательство положения 2 дает эффективный общий метод, с помощью которого для любой тождественно-истинной формулы по ее таблице можно построить доказательство данной формулы в системе N. Из положения 2 вытекает следствие.
Если формулы А, В равносильны, то в системе N доказуема формула А→В.

Полнота классического исчисления высказываний.







Покажем , что система N естественного вывода семантически полна, отложив установление ее семантической корректности. Будем говорить, что формула

Слайд 78 Логика - это наука о способах доказательства. Выясним, в чем,

собственно, состоит различие в построении доказательств в логике высказываний и

логике Буля.
В булевой логике все доказательства строились на отношении эквивалентности. Две логические функции считались эквивалентными, если они давали на соответствующих наборах аргументов абсолютно одинаковые значения нулей и единиц. При использовании формальной записи логических выражений отдельные звенья цепи любого доказательства там были связаны через символ равенства "=". Отношение эквивалентности удовлетворяет трем законам -
рефлексивности: А = А;
симметричности: если А = В , то В = А; транзитивности: если А = В и В = С, то А = С.
В логике высказываний все доказательства строятся на отношении порядка, т.е. на отношении, которое существует между причиной и следствием. В логике Буля используются два символа эквивалентности - " ~ " и " = ". Символ " ~ " является объектным, а " = " - субъектным. Таким образом, следует различать язык логики высказываний и метаязык исследователя.

Построение доказательств в логике высказываний.







Логика - это наука о способах доказательства. Выясним, в чем, собственно, состоит различие в построении доказательств в

Слайд 79 Введем еще два метасимвола: вместо объектной конъюнкции " /\ "

будем использовать субъектный символ метаконъюнкции - " , ", а

вместо объектной дизъюнкции " \/ " - субъектную метадизъюнкцию " ; ".
Утверждение, требующее доказательства, в логике высказываний оформляется в виде следующего причинно-следственного отношения:
Р1,Р2,...,Рn -1,Рn С где Рi - посылка (причина), С - заключение (следствие). Читается: "Если посылки P1,Р2,...,Рn -1,Рn истинны, то заключение С тоже истинно" или, по-другому: "Если причины P1,Р2,...,Рn-1,Рn имели место, то будет иметь место и следствие С".
Р1,Р2,...,Рn -1,Рn С - называется клаузой (clause).
Клауза - это метапредложение, в котором использовано отношение порядка, оформленное через символ метаимпликации " ".

Построение доказательств в логике высказываний.







Введем еще два метасимвола: вместо объектной конъюнкции

Слайд 80 Клауза есть именно формальная запись доказываемого предложения. Вместо букв в

ней можно подставить объектные высказывания, и тогда клауза наполняется конкретным

содержанием, которое уже именуется семантикой или легендой. Над субъектом, который формулирует метапредложения, может стоять другой субъект, для которого уже предложения первого субъекта окажутся объектными. Тогда клаузу Р1,Р2,...,Рn -1,Рn С второй субъект или метасубъект запишет для себя следующим логическим выражением:
(Р1 → Р2 →... → Рn-1 → Рn)→C.
Преобразовав это выражение в дизъюнкт, получим:
~Р1 \/ ~Р2...\/ ~Рn-1 → ~Рn \/ С.
Отсюда легко находим:
(Р1/\Р2/\.../\Рn-1)→(~Рn\/ С).
Поэтому исходная клауза может быть представлена в другой эквивалентной форме:
Р1,Р2,...,Рn-1 ~Рn;С.
В силу коммутативности конъюнкции на месте посылки Рn может оказаться любая другая, причем не одна. Например, клауза:
Р1, Р2, Р3, Р4 C1 ; C2; C3
может быть преобразована в другую эквивалентную форму:
Р4, ~C2, Р1, ~C1 ~Р1 ; C3; ~Р2.








Построение доказательств в логике высказываний.

Клауза есть именно формальная запись доказываемого предложения. Вместо букв в ней можно подставить объектные высказывания, и тогда

Слайд 81 Однако исходная клауза по сравнению с другими подобными формами, имеет

определенные преимущества и, в частности, используется в языке логического программирования

ПРОЛОГ. Ее называют хорновской. Произвольную клаузу всегда можно свести путем эквивалентных преобразований к хорновскому виду.
Если символ метаимпликации " " клаузы сместить в крайнее левое положение, то она превратится в тавтологию', если же его сместить в крайнее правое положение, то - в противоречие:
1 ~Р1; ~Р2; ... ; Рn-1; Рn; С - тавтология,
Р1, Р2,..., Рn-1, Рn, Рn, ~С 0 - противоречие.
Аксиоматическое построение логики высказываний состоит в том, чтобы попытаться вычленить из бесконечного числа истинных клауз независимую систему аксиом, с помощью которой можно было бы установить справедливость любых других клауз.







Построение доказательств в логике высказываний.

Однако исходная клауза по сравнению с другими подобными формами, имеет определенные преимущества и, в частности, используется в

Слайд 82 В качестве основной аксиомы логики высказываний, выражающей отношение порядка, мы

возьмем клаузу А,В А, .








Построение доказательств в логике высказываний.

В качестве основной аксиомы логики высказываний, выражающей отношение порядка, мы возьмем клаузу А,В А, .

Слайд 83 Закона о единице записывается как:
А, 1 А ,
Закон

транзитивности :
А→В, В→С А→С,







Построение доказательств в логике высказываний.

Закона о единице записывается как:А, 1 А , Закон транзитивности : А→В, В→С А→С,

Слайд 84 Противоположным к аксиоматическому является конструктивный метод доказательства, основанный на таблицах

истинности.






Построение доказательств в логике высказываний.

Противоположным к аксиоматическому является конструктивный метод доказательства, основанный на таблицах истинности.

Слайд 85 Правило отделения:
А, А→В В
Принцип резолюций целиком заменяет аксиому порядка,

поскольку сама эта аксиома может быть доказана в рамках метода

резолюций.
Действительно, А, В А, А, В, 0 , О, В 0.
Обращаем внимание на то, что посылка В здесь вообще не используется. Это необходимо иметь в виду: необязательно использовать все посылки (их число часто бывает избыточным) - главное получить ноль.







Построение доказательств в логике высказываний.

Правило отделения:А, А→В В Принцип резолюций целиком заменяет аксиому порядка, поскольку сама эта аксиома может быть доказана

Слайд 86 Доказательный вывод в натуральном исчислении строится как упорядоченная цепь преобразований,

связанных с удалением или введением логических связок на основе следующих

десяти правил:
1) правило введения конъюнкции (ВК) - ( А) & ( В) А /\ В ;
2) правило удаления конъюнкции (УК) - А /\ В А ;
3) правило введения импликации (ВИ) - В А→В ,  А В А→В;
4) правило удаления импликации (УИ) - ( А) & ( А→В) В ,  А→В // А В ;
5) правило введения дизъюнкции (ВД) - А A \/ В ;
6) правило удаления дизъюнкции (УД) - ( A \/ В) & (А С) & (В С) С ;
7) правило введения отрицания (ВО) - А, В 0 // А ;
8) правило удаления отрицания (УО) - (А ) & (А В) // А 0;
9) правило введения эквивалентности (ВЭ) - (А В) & (В А) А ↔ В;
10) правило удаления эквивалентности (УЭ) - А ↔ В // (А В) & (В А).
Эти правила надо понимать так: если слева от символа " // " стоят истинные клаузы, то справа от символа " // " тоже будут стоять истинные клаузы. Например, первое правило введения конъюнкции можно прочитать следующим образом: если высказывания А и В (связка "и" передается знаком " & ") порознь истинные (о чем говорят рядом стоящие с этими буквами символы метаимпликации " "), то будет истинной и их конъюнкция А и В.







Построение доказательств в логике высказываний.

Доказательный вывод в натуральном исчислении строится как упорядоченная цепь преобразований, связанных с удалением или введением логических связок

Слайд 87 Во всех десяти правилах перед символом метаимпликации " "

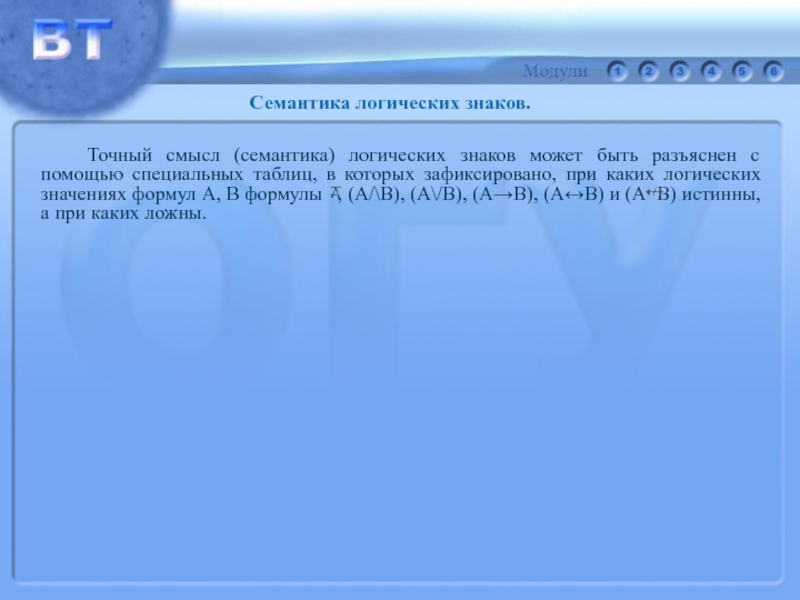
может стоять любой перечень посылок Р. Так, десятое правило может

выглядеть следующим образом:
Р А ↔ В // (Р, А В) & (Р, В А).
Кроме перечисленных десяти правил, имеется еще одно - базовое правило (БП), которое сначала сформулируем словами: во-первых, любая посылка может выступать в роли следствия, т.е.
А, В, С А ,  А, В, С В и А, В, С С
будут всегда истинными и не требуют доказательства, т.к. удовлетворяют аксиоме порядка; во-вторых, в перечень посылок истинной клаузы всегда можно добавить новые посылки, т.е. если клауза
А, В, С X
верна, то будут истинными и все клаузы, построенные на ее основе -
А, В, С, D X ,  А, В, С, ... X.
В обобщенной форме базовое правило можно записать так:
Р X // Р, Y X ,
где X - любая посылка из Р, a Y - произвольная посылка.
Действенность метода натурального исчисления продемонстрируем на примере следующей тавтологии:
1 (А→В)→((А→ )→ ).







Построение доказательств в логике высказываний.

Во всех десяти правилах перед символом метаимпликации

Слайд 88 Доказательство:
1. А, А→В В, (УИ)
2. А, А→

(УИ)
3. А, А→В, А→ B

В(1, БП)
4. А, А→ , А→В (2, БП)
5. А, А→В, А→ 0 (3,4, УО)
6. А→В, А→ (5, ВО)
7. А→В (А→ )→ (6, ВИ)
8. 1 (А→В)→((А→ )→ ). (7, ВИ)







Построение доказательств в логике высказываний.

Доказательство: 1. А, А→В В, (УИ) 2. А, А→ (УИ) 3. А, А→В, А→

Слайд 89Модуль 6.
Исчисление предикатов. Символизация естественного языка.
Тема 1: Понятие предиката, предикатного

выражения и кванторов.
Тема 2: Исчисление предикатов. Общезначимость.
Тема 3: Тождественно истинные

формулы логики предикатов.

Тема 4: Логическое следование.

Тема 5: Естественный вывод в логике предикатов.

Тема 6: Специфические законы логики предикатов.







Модуль 6.Исчисление предикатов. Символизация естественного языка.Тема 1: Понятие предиката, предикатного выражения и кванторов.Тема 2: Исчисление предикатов. Общезначимость.Тема

Слайд 90Понятие предиката, предикатного выражения и кванторов.
В грамматике предикат (сказуемое) есть

то слово (или несколько слов) в предложении, которое выражает то,

что говорится о субъекте (подлежащем) . В логике "предикат" употребляется в более общем смысле, чем в грамматике. Вводя в предикат переменную, замещающую предмет (например,"x есть действительное число"), мы получаем назывательную функцию в том смысле, что для каждого значения переменной (из соответствующей области определения) результат есть высказывание.
Результатом является понятие об n-местном предикате как о выражении, обладающем тем свойством, что, приписав значения х1, х2, ... хn из соответствующих областей определения, мы получаем высказывание. Для удобства в число значений п включаем и под 0-местным предикатом высказывание.







Понятие предиката, предикатного выражения и кванторов. В грамматике предикат (сказуемое) есть то слово (или несколько слов) в предложении,

Слайд 91 Выражение "для всякого x" называется квантором общности. Мы считаем "для

каждого x" и "для всех x" выражающими одинаковый смысл.
Подобным же

образом, предписав S(x) выражение "существует х (такое, что)", получаем высказывание, имеющее тот же смысл, что и "существуют второкурсники". Выражение "существует x" называется квантором существования.







Понятие предиката, предикатного выражения и кванторов.

Выражение

Слайд 92 Исчисление предикатов. Общая формулировка
Для каждого n = 0, 1, 2,

... дано некоторое число n - местных предикатов (или высказывательных

функций от n переменных). Будем обозначать их символически через Р(х, у), Р(х, у, z).
Понятие формулы логики предикатов
Пользуясь данным множеством предикатных символов, мы образуем выражения, которые будем называть "формулами (исчисления предикатов)". Простая (или элементарная) формула есть выражение, получающееся из предикатного символа подстановкой в него вместо переменных, входящих в предикатный символ, каких-либо (не обязательно различных) переменных.







Понятие предиката, предикатного выражения и кванторов.

Исчисление предикатов. Общая формулировка Для каждого n = 0, 1, 2, ... дано некоторое число n - местных

Слайд 93 Если А и В - элементы данного множества, то элементами

его будут и ~ (А), (А) & (В), (А) V

(В), (А) -> (В) и (А)<->(В).
Если А - элемент данного множества, а х - переменная, то (x)А и (Е х)А - тоже элементы этого множества. Элементы такого расширенного множества называются формулами, те из них, которые не являются простыми, называются составными формулами.







Понятие предиката, предикатного выражения и кванторов.

Если А и В - элементы данного множества, то элементами его будут и ~ (А), (А) &

Слайд 94 Вхождение переменной в формулу называется связанным, если оно находится

в области действия квантора, использующего эту переменную, или же оно

является вхождением в этот квантор. Вхождение переменной в формулу называется свободным, если оно не является связанным.
Например,
(x)Р(х, у)
оба вхождениям связанные, а единственное вхождение y в данную формулу является свободным.







Понятие предиката, предикатного выражения и кванторов.

Вхождение переменной в формулу называется связанным, если оно находится в области действия квантора, использующего эту переменную,

Слайд 95Исчисление предикатов. Общезначимость.
Примем, что простой формуле Р(y1, y2, ... yn)

приписывается истинностное значение, связанное с приписыванием элементов из поля D

каждой переменной из числа y1, y2, ... уn, следующим образом. Если переменной уi приписывается элемент di поля D и если предикатному символу Р (x1, x2, ... хn) приписывается значение f, то истинностное значение для Р(у1, у2, ... уn) будет f (d1, d2, ... dn).
Например, если Р(х, у, х) есть простая формула и формуле Р (х, у, z) приписывается значение f, то истинностное значение Р (х, у, х), связанное с приписыванием элемента a переменной х и элемента в переменной y, будет f(а, в, a).







Исчисление предикатов. Общезначимость. Примем, что простой формуле Р(y1, y2, ... yn) приписывается истинностное значение, связанное с приписыванием элементов

Слайд 96Тождественно истинные формулы логики предикатов.
Напомним, что как и в логике

высказываний, формула, имеющая на выходе только значения 1, называется тождественно-истинной

формулой (логической тавтологией) и обозначается с помощью специального логического знака - ╞.
Запись формулы ╞ А говорит о том, что формула А - тождественно-истинная формула.
Такими же формулами логики предикатов будут следующие формулы:
1. ╞ (x) P(x) -> P(x)
2. ╞ P(x) -> (E x) P(x)
3. Если (х) Р(х) V (x) Q(х), то ╞(х) (Р(х) V Q(х))
4. ╞ Р(х)->(Ех) Р(х)
5. ╞ (х) Р(х)-> ╞ Р(х)
6. Если Q -> Р(х), то ├ Q -> (х) Р(х)
7. Если Р(х) -> Q, то ╞ (Е х) Н(х) -> Q







Тождественно истинные формулы логики предикатов. Напомним, что как и в логике высказываний, формула, имеющая на выходе только значения

Слайд 97Логическое следование.
Основное определение понятия логического следования для логики предикатов.
Формула В

есть логические следствие формул А1, А2, .... Аn, что выражается

следующей записью - А1, А2, .... Аn > В , если и только если для каждого поля В формула В получает значение 1 каждый раз, как каждое значение А получает значение 1. Если переменная х входит как свободная в какую-то формулу А, то при каждом приписывании значений формулам А для всех свободных вхождений х в поле В выбирается одно и то же значение, т.е., выбирая приписывание значений формулам А, такое х рассматривается как постоянная.







Логическое следование. Основное определение понятия логического следования для логики предикатов. Формула В есть логические следствие формул А1, А2, ....

Слайд 98Естественный вывод в логике предикатов.
Подстановкой в формулу А переменной у

вместо переменной х называется замещение в А всех свободных вхождений

х вхождениями у. Результат подстановки в формулу А мы обозначаем посредством А (х - у). Если х не входит свободно в А, то мы считаем, что А (х - у) совпадает с А. Очевидно, что если у совпадает с х, А (х - у) также совпадает с А, т. е. в этом случае подстановка не изменяет формулу, в которую производится подстановка.
Подстановка у в А вместо х называется корректной, если ни одно введенное данной подстановкой вхождение у не оказывается связанным в А (х - у). Иначе говоря, вводимое подстановкой вхождение переменной не должно попадать в область действия квантора, связывающего данную переменную.
Система естественного вывода в логике предикатов (натурального вывода).
Ниже в схемах правил А, С - формулы, х, у - переменные, А (х - у) - результат корректной подстановки у в А вместо х:
ВВ  А (х - у) (х)А
УВ     (х)А    А (х - у)







Естественный вывод в логике предикатов. Подстановкой в формулу А переменной у вместо переменной х называется замещение в А

Слайд 99Естественный вывод в логике предикатов.
ВС  А (х-у)

Е х А
УС

 Е х А А(х - у) → С C







Естественный вывод в логике предикатов. ВС  А (х-у)

Слайд 100 Правило ВВ называется введением всеобщности, правило ВС - введением существования,

и, наконец, правило УС -удаление существования. Можно заметить известную аналогию

между ВВ, УВ и ВК, УК, с одной стороны, и ВС, УС и ВД, УД - с другой.
Переменная, обозначенная в схемах правил ВВ и УС посредством у, называется собственной переменной этих правил. При построении доказательств правила ВВ и УС применяются с ограничениями, относящимися к собственной переменной.
Ограничения на применение правил ВВ, УС
При построении доказательства правило ВВ применяется, если выполняются следующие условия:
собственная переменная данного правила не входит свободно в формулы, написанные ранее в качестве допущений (в том числе и в качестве допущения косвенного доказательства);
собственная переменная не входит свободно в формулу, обозначенную в схеме правила посредством (х) А (т. е. в заключение данного правила).







Естественный вывод в логике предикатов.

Правило ВВ называется введением всеобщности, правило ВС - введением существования, и, наконец, правило УС -удаление существования. Можно

Слайд 101При построении доказательства правило УС применяется, если выполняются следующие условия:


собственная переменная данного правила не входит свободно в формулы, ранее

написанные в качестве допущений (в том числе и в качестве допущения косвенного доказательства);
собственная переменная не входит свободно ни в формулу, обозначенную посредством Е х А, ни в формулу, обозначенную посредством С, в схеме правила УС (т. е. ни в левую посылку, ни в заключение данного правила).
Правило УВ можно охарактеризовать как правило логического перехода от общего предложения к рассмотрению его частного случая.







Естественный вывод в логике предикатов.

При построении доказательства правило УС применяется, если выполняются следующие условия: собственная переменная данного правила не входит свободно

Слайд 102Правило ВВ
Оно позволяет переходить от предложения, выражающего условие, к общему

предложению, если от параметра данного условия не зависят:

1) ни допущения доказательства,
2) ни заключение данного правила.
Поясним сначала существенность второго ограничения на применение правила ВВ. Так, логически некорректный (ошибочный) переход от истинного арифметического равенства у = у к ложной арифметической формуле А (х) (х=(у)), означающей, что любые числа равны между собой, объясняется, как нетрудно убедиться в том, чтоу, как собственная переменная данного правила, входит свободно в (х) (х = у), т. е. (х) (х = у) зависит от параметра у.
Правило УС
Правило УС связано со следующим способом рассуждения. Располагая предложением Е хА, утверждающим существование предмета (объекта), удовлетворяющего условию А, мы допускаем, что таким объектом является, скажем, объект, представленный параметром у, от которого не зависят ни допущение доказательства, ни предложение Е хА. Затем, получив условное предложение (импликацию) А (х - у) → С, где С также не зависит от параметра у, мы с помощью правила УС переходим к заключению С.







Естественный вывод в логике предикатов.

Правило ВВ Оно позволяет переходить от предложения, выражающего условие, к общему предложению, если от параметра данного условия не

Слайд 103Специфические законы логики предикатов.
С помощью сформулированных выше правил естественного вывода

доказываются следующие формулы, которые выражают собой специфические законы логики предикатов:
1. (х)А->

А(х - у)
2. А (х) -> Е х А
3. (х)А -> Е х А
4. (х) А (у) А <-> (у) (х) А
5. Е х Е у А<-> Е у Е х А
6. Е х (у) А -> (х) Е у А
7. (х) (А -> В) -> ((х) А -> (х) В)
8. (х) (А -> В) <-> (А-> (х) В), где х не входит свободно в А
9. (х) (А -> В)-> (Е х А -> Е х В)
10. (х) (А -> В) <->(Е х А -> В), где x не входит свободно в В
11. (х) (А & В) <-> ((х)А & (х) В)
12. (х) (А & В) <-> (А & (х) В), ...







Специфические законы логики предикатов. С помощью сформулированных выше правил естественного вывода доказываются следующие формулы, которые выражают собой специфические

Слайд 104Специфические законы логики предикатов.
13. Е х (А & В)-> (Е х

А & Е х В)
14. Е х (А & В)

(А & Е х В), ...
15. ((х) А v (х) В) -> (х) (А v В)
16. Е х (А v В) <-> (Е х А v Е х В
17. (х) А <-> А, когда х не входит свободно в А
18. Е х А <-> А, когда х не входит свободно в А
19. А (х) -> ~(х) А
20. ~ Е х А-> ~ А(х)
21. ~ Е х А->~ (х)А
22. ~ (х) А <-> Е х ~ А
23. ~ Е х А <-> (х) ~ А
24. (х) А <-> Е х ~ А
25. Е х А <-> ~ (х) ~ А
26. Е х (А -> В) <->((х) А -> Е х В)







Специфические законы логики предикатов. 13. Е х (А & В)-> (Е х А & Е х В) 14. Е х (А

Слайд 105 27. Е х (А -> В) (А -> Е х

В), где х не входит свободно в А
28. Е х (А

-> В) <-> ((х) А -> В), где х не входит свободно в В
29. (x) (А v В) <-> (А v (х) В), где х не входит свободно в А
Формулы 4 и 5 называются законами перестановки кванторов. Согласно этим законам начинающие формулу однородные кванторы вместе с их переменными можно менять местами.
Формулы 7-16 называются законами пронесения кванторов. В них указываются условия, при которых кванторы можно вносить в область действия или выносить из области действия бинарной пропозициональной связки, т.е. знака конъюнкции, дизъюнкции и импликации.
Формулы 17-18 выражают принципы так называемых вырожденных кванторрв, которые не имеют в управляемой ими формуле свободных вхождений переменных, связываемых этими кванторами. Согласно этим принципам можно избавляться от вырожденных кванторов.
Формулы 19-25 называются законами отрицания кванторов. Формулы 22-23 называются законами де Моргана для кванторов. Формула 24-25 доказуемы только в классическом исчислении предикатов.







Специфические законы логики предикатов.

27. Е х (А -> В) (А -> Е х В), где х не входит свободно в А 28. Е

Похожие презентации

Тема № 7 Передвижение и расположение подразделений на месте Тема № 7 Передвижение и расположение подразделений на месте 298
17_IBS 17_IBS 470
Роль религии в современном мире Роль религии в современном мире 246
Знаем правила прекрасно - соблюдаем не напрасно Знаем правила прекрасно - соблюдаем не напрасно 186
Звіт про рух грошових коштів Звіт про рух грошових коштів 394
Ткани животных Ткани животных 192
Раздел Художественная культура Средневековья Раздел Художественная культура Средневековья 230
Виртуальная выставка Виртуальная выставка 221
Психофизиология функциональных состояний Психофизиология функциональных состояний 349
Беркли и Юм Субъективный идеализм МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ Беркли и Юм Субъективный идеализм МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ 241
Повреждение вращательной манжеты Повреждение вращательной манжеты 249
вар 6-2 новая.ppt вар 6-2 новая.ppt 231
ТЕМА 3.1 Общие сведения о технических средствах таможенного контроля ДРМ ТЕМА 3.1 Общие сведения о технических средствах таможенного контроля ДРМ 530
ЛОГИКА Теория и практика аргументации СМИРНОВА О.М. Кандидат философских ЛОГИКА Теория и практика аргументации СМИРНОВА О.М. Кандидат философских 304
Железнодорожный путь Практические занятия для студентов 3 курса 2 семестра Железнодорожный путь Практические занятия для студентов 3 курса 2 семестра 314
КНАУ Кафедра гидротехническое строительство КНАУ Кафедра гидротехническое строительство 251
Тема 7. Процесс производства и результаты деятельности предприятия Тема 7. Процесс производства и результаты деятельности предприятия 271
Природознавство. 2 клас Тема 2. Природа зимою Урок № 26 Тема уроку: Погода зимою Природознавство. 2 клас Тема 2. Природа зимою Урок № 26 Тема уроку: Погода зимою 196
Юрий Яковлев Юрий Яковлев 881
Защита от электрического тока Защита от электрического тока 306

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика