Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Содержание: Элементы теории алгоритмов. Формализация представления
Содержание
- 1. Содержание: Элементы теории алгоритмов. Формализация представления
- 2. Элементы теории алгоритмов.Тема 1: Нестрогое определение алгоритма.Тема
- 3. Компьютер нужен человеку для решения задач практики.
- 4. В связи с этим возникает ряд взаимосвязанных
- 5. Начнем с рассмотрения элементов теории алгоритмов. Это
- 6. Исторически термин "алгоритм" произошел от фамилии узбекскогоматематика
- 7. В связи с этим возникает вопрос: можно
- 8. Элементарность шагов: закон получения последующей системы величин
- 9. Любая программа есть ни что иное, как
- 10. В теоретических подходах к построению строгого определения
- 11. Данный подход развивался в работах Э.
- 12. 1.Исполнитель алгоритма - это субъект или устройство
- 13. При построении алгоритма для такого исполнителя разработчику
- 14. 2. Допустимость нестрогой
- 15. Введем ряд определений. Пусть имеются два множества
- 16. В данном подходе любой алгоритм, единый для
- 17. Совокупность вычислимых функций для самых разных понимании
- 18. Перечисленные простейшие функции всюду определены и интуитивновычислимы.
- 19. Говорят, что функция h получена из функций
- 20. Поскольку областью определения функций является множество всехнатуральных
- 21. Частичная функция f(x1, ..., xn) называется примитивно
- 22. Подобным же образом определяется функция многих переменных: fi(x1,
- 23. Понятие частично рекурсивной функции является одним из
- 24. Понятие частично рекурсивной функции научным эквивалентом интуитивногопонятия
- 25. Общие подходы. Алгоритмические
- 26. перед началом работы машине предоставляются исходные данные
- 27. Алгоритм - это любая конечная система правил
- 28. Таким образом, все возможные алфавитные преобразования сводится
- 29. Алгоритмическая машина Поста Пост, в отличие от Тьюринга,
- 30. Условимся обозначать головку знаком "V" над обозреваемой
- 31. Алгоритм как абстрактная машина.
- 32. В отличие от этой ситуации, остановка по
- 33. Можно показать, что с помощью машины Поста
- 34. Алгоритмическая машина Тьюринга Машина Тьюринга состоит из трех
- 35. Информация, хранящаяся на ленте, изображается конечной последовательностьюзнаков
- 36. Эта система команд обработки дополняется также предельно
- 37. Общее правило, по которому
- 38. Это означает, что логический блок реализует функцию,сопоставляющую
- 39. В зависимости от начальной конфигурации возможны два
- 40. Всякий алгоритм может быть задан посредством тьюринговой
- 41. Алгоритм задается системой подстановок,которые указывают, какие
- 42. Алгоритмом в алфавите А называется эффективно вычислимаяфункция,
- 43. Процесс прекращается в двух случаях: либо в
- 44. Различные варианты решения проблемы формулировки точного определенияалгоритма
- 45. Основные понятия теории алгоритмов – вычислимаяфункция и
- 46. Рассмотренный тезис Черча, утверждает, что всякая частично
- 47. Также была доказана теорема о сводимости одной
- 48. Задача считается алгоритмически неразрешимой, если не существуетмашины
- 49. В теории алгоритмов к алгоритмически неразрешимой относится
- 50. Неразрешимой оказывается и проблема распознавания эквивалентностиалгоритмов: нельзя
- 51. Сложность алгоритма. Исполнение любого алгоритма требует определенного
- 52. Обсуждать будем временную сложность алгоритмов. Время работы алгоритма
- 53. При этом, безусловно, предполагается, что во всех
- 54. Для сопоставления в таблице ниже приведены данные
- 55. Из таблицы видно, что, например, для экспоненциального
- 56. Сложность алгоритма.
- 57. Сложность алгоритма.
- 58. Слайд 58
- 59. Формальные языки.
- 60. Формальные языки.
- 61. Формальные языки.
- 62. Способы представления алгоритмов.
- 63. Способы представления алгоритмов.
- 64. Способы представления алгоритмов.
- 65. Способы представления алгоритмов.
- 66. Способы представления алгоритмов.
- 67. Способы представления алгоритмов.
- 68. Способы представления алгоритмов.
- 69. Способы представления алгоритмов.
- 70. Пример команд ассемблера: CLA - очистить один
- 71. Способы представления алгоритмов.
- 72. Примерами являются язык FORTRAN (FOFtmula TRANsiator) -язык
- 73. Графическая форма записи Другое распространенное название данной формы
- 74. Способы представления алгоритмов.
- 75. Идеи структурного программирования были высказаны в 1965
- 76. каждый блок выполняется не более одного раза;
- 77. Очевидно несколько блоков, связанных линейным потоком управления,
- 78. Третий тип потока управления называется циклическим -
- 79. Структурная теорема.
- 80. Структурная теорема.
- 81. Структурная теорема.
- 82. Литература.
- 83. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Элементы теории алгоритмов.
Тема 1: Нестрогое определение алгоритма.
Тема 2: Рекурсивные функции.
Тема
3: Алгоритм как абстрактная машина.
Тема 4: Нормальные алгоритмы Маркова.
Тема 5:
Сопоставление алгоритмических моделей.Тема 6: Проблема алгоритмической разрешимости.
Тема 7: Сложность алгоритма.
Модуль 1.
Слайд 3 Компьютер нужен человеку для решения задач практики.
Просматриваются общие моменты
в порядке их решения:
- во-первых, требуется выделить систему и построить
ее информационную модель.- во-вторых, должен быть установлен порядок обработки данных.
В общем случае обработка состоит в преобразовании по некоторым правилам
исходной данных, в результате чего появляются новые данные. Преобразование должно осуществлять некоторое техническое устройство в автоматическом режиме.
Алгоритмы. Модели. Системы.
Слайд 4 В связи с этим возникает ряд взаимосвязанных задач, требующих
разрешения:
определение
правил обработки информации с учетом того, что она представлена в
дискретной форме;установление, каким требованиям должно удовлетворять устройство, производящее обработку;
определение того, каким образом данные и последовательность обработки может быть представлена для исполнения устройству.
Общие подходы к решению проблем обработки дискретной информации изучаются в теории алгоритмов.
Алгоритмы. Модели. Системы.
Слайд 5Начнем с рассмотрения элементов теории алгоритмов. Это рассмотрение будет
построено в
два этапа; на первом, приводится возможно более строгое определение
алгоритма и
обсуждаются его свойства, а на втором изучаются теоретические моделиалгоритмов, а также исследуется проблема алгоритмической разрешимости задач.
Элементы теории алгоритмов.
Слайд 6 Исторически термин "алгоритм" произошел от фамилии узбекского
математика IX века Мухаммеда
ибн Муса ал-Хорезми, который впервые
сформулировал правила четырех основных арифметических действий.
Поначалуименно эти правила назывались алгоритмами, но затем термин получил дальнейшее
развитие в первую очередь в математике - алгоритмом стал называться любой способ
вычислений, единый для некоторого класса исходных данных, например, нахождение
производной функции. Одна из важнейших задач обучения математике состоит именно
в освоении общих вычислительных алгоритмов.
Нестрогое определение алгоритма.
Слайд 7 В связи с этим возникает вопрос: можно ли построить общее
и точное
определение алгоритма .
Алгоритм - это точно определенная (однозначная) последовательность
простых (элементарных) действий, обеспечивающих решение любой задачи из некоторого класса. Понятие можно уточнить, указав перечень общих свойств, которые характерны
для алгоритмов. К ним относятся:
Дискретность алгоритма означает, что алгоритм разделен на отдельные шаги (действия), причем, выполнение очередного шага возможно только после завершения всех операций на предыдущем шаге. При этом набор промежуточных данных конечен и он получается по определенным правилам из данных предыдущего шага.
Детерминированность алгоритма состоит в том, что совокупность промежуточных величин на любом шаге однозначно определяется системой величин, имевшихся на предыдущем шаге.
Нестрогое определение алгоритма.
Слайд 8
Элементарность шагов: закон получения последующей системы величин из предыдущей должен
быть простым и локальным. Какой шаг (действие) можно считать элементарным,
определяется особенностями исполнителя алгоритма.Направленность апгоритма: если способ получения после дующих величин из каких-либо исходных не приводит к результату, то должно быть указано, что следует считать результатом алгоритма.
Массовость алгоритма: начальная система величин может выбираться из некоторого множества.
Нестрогое определение алгоритма.
Слайд 9 Любая программа есть ни что иное, как запись алгоритма на
языке, который
может "понять" исполнитель - компьютер.
Уточнение понятия алгоритма производится
в рамках алгоритмических моделей.Модель определяет набор средств, использование которых допустимо при решении
задачи, т.е. перечень элементарных шагов, способы определения следующего шага и
т.п. Алгоритмические модели могут быть теоретическими и практическими.
Нестрогое определение алгоритма.
Слайд 10 В теоретических подходах к построению строгого определения понятия
алгоритма исторически выделились
три основные направления.
Первое направление связано с рассмотрением алгоритмов, позволяющих
вычислить значение
числовых функций, зависящих от целочисленных значенийаргументов - такие функции получили название вычислимых.
Благодаря работам А.Черча, К. Геделя, С. Клини, была обоснована
тождественность класса всюду определенных вычислимых функций с классом
частично рекурсивных функций, который определяется строго. Это позволило свести
проблему алгоритмической разрешимости к доказательству возможности (или
невозможности) построения рекурсивной функции, решающей задачу. Второе направление связано с машинной
математикой. Основная идея этого направления состоит в том, что алгоритмические
процессы - это процессы, которые может совершать соответствующим образом
устроенная "машина".
Нестрогое определение алгоритма.
Слайд 11 Данный подход развивался в работах Э. Поста и А.
Тьюринга одновременно с упомянутым выше подходом. Доказательство алгоритмической разрешимости задачи
сводится к доказательству существования машины, ее решающей.Третье направление связано с понятием нормальных алгоритмов, введенным и
разработанным российским математиком А. А. Марковым в начале 50-х гг. XX в.
Нестрогое определение алгоритма.
Слайд 12 1.Исполнитель алгоритма - это субъект или устройство способные правильно интерпретировать
описание алгоритма и выполнить содержащийся в нем перечень действий.
Указания по
выполнению действий для каждого исполнителя формулируютсяпосредством некоторого языка, включающего набор служебных слов, обозначающих
действия (команды), а также синтаксические правила их объединения. Совокупность
допустимых команд образует систему команд исполнителя (СКИ). Различаться СКИ
разных исполнителей могут детальностью описания действий. Элементарным
(простейшим) действием при обработке дискретной информации является замена
одного знака другим. Однако можно построить абстрактное или реальное устройство,
которое будет способно выполнять целую цепочку подобных
элементарных действий по заложенному в него правилу - некое комплексное
(интегральное) действие.
Нестрогое определение алгоритма.
Слайд 13 При построении алгоритма для такого исполнителя разработчику достаточно
указать последовательность интегральных
команд, а их преобразование в цепочку
истинно элементарных шагов будет производиться
самим исполнителем. Истинно элементарными следует считать действия процессора - их называют
машинными командами, а их обозначения - машинными кодами. Первым (низшим)
уровнем, на котором происходит отход от машинных кодов, является код ассемблера –
внутренний (т.е. аппаратно-зависимый) язык.
Нестрогое определение алгоритма.
Слайд 14 2. Допустимость нестрогой формализации представления алгоритмов,
если исполнителем является человек.
3. Расширение применимости
понятия алгоритма на последовательность любых дискретных действий.Нестрогое определение алгоритма.
Слайд 15 Введем ряд определений.
Пусть имеются два множества X и У.
Если некоторым элементам множества X поставлены в соответствие однозначно
определенные элементы множества У, то говорят, что задана частичная функция из Х в У.Совокупность тех элементов множества X, у которых есть соответствующие элементы в У, называется областью определения функции, а совокупность тех элементов У, которые соответствуют элементам X, называются совокупностью значений функции.
Если область определения функции из X е Y совпадает с множеством X, то функция называется всюду определенной.
Исходная идея построения точного определения алгоритма, опирающегося на
понятие рекурсивной функции, состоит в том, что любые данные (безусловно,
дискретные) можно закодировать натуральными числами в некоторой системе
счисления, и тогда всякое их преобразование сведется к последовательности
вычислительных операций, а результат обработки также будет представлять собой
целое число.
Рекурсивные функции.
Слайд 16 В данном подходе любой алгоритм, единый для данной числовой функции,
вычисляет
ее значение, а его элементарными шагами оказываются обычные
арифметические и логические
операции. Такие функции получили названиевычислимых.
Функция y(x1, x2,...,xn) называется эффективно вычислимой, если существует
алгоритм, позволяющий вычислить ее значение по известным значениям аргументов.
Рекурсивные функции.
Слайд 17 Совокупность вычислимых функций для самых разных понимании процессов,
удовлетворяющих перечисленным условиям,
оказалась одной и той же и притом легко
описываемой в обычных
математических терминах. Эта точно описанная совокупностьчисловых функций, совпадающая с совокупностью всех вычислимых функций, носит
название совокупности рекурсивных функций.
В рекурсивной модели "элементарными шагами" являются так называемые простейшие числовые функции S1 0n и Inm,
комбинацией которых строятся все более сложные и которые определяются
следующим образом:
S1(x)=x+1 - это одноместная (т.е. имеет один аргумент) функция непосредственного следования;
0n(x1, x2, ..., sn)=0 - это n-местная функция тождественного равенства нулю;
Inm(x1, ..., xn)=xm (1<=т<=п ;п= 1, 2, ...) - n-местная функция тождественного повторения значения одного из своих аргументов.
Рекурсивные функции.
Слайд 18 Перечисленные простейшие функции всюду определены и интуитивно
вычислимы. Частичные функции, которые
можно получить при помощи этих
операторов из простейших функций называются частично
рекурсивными. Гипотеза Черча состоит в том, что класс построенных таким образом частично рекурсивных функций совпадает с классом функций, допускающим алгоритмическое вычисление.
Суперпозиция частичных функций
Пусть m-местные функции
f1(x1, ..., xm),f2(x1, ..., xm),f3(x1, ..., xm)
подставляются в n-местную функцию g(x1,…, xn). В результате получается n-местная функция
h(x1, ..., xn)=g(f1(x1, ..., xn), ..., fn(x1, ..., xn)
Рекурсивные функции.
Слайд 19 Говорят, что функция h получена из функций g, f1, ...,
fn суперпозицией (или
подстановкой). Символически такая подстановка обозначается следующим образом:
Sn+1(g,f1, ...
,fn), где индекс сверху обозначает количество функций, подставляемых вкачестве аргументов.
Если вычислимы функции g, f1, ..., fn, то функция h также может быть
вычислена. Ясно также, что если все функции g, f1, ...., fn всюду определены, то и
функция h также всюду определена.
Таким образом, если функции g, f1, ...,fn интуитивно вычислимы, то будет
интуитивно вычислимой и функция h.
Примитивная рекурсия
Пусть заданы какие-либо числовые частичные функции: n-местная g(х1, ..., хn) и
(n+2)-местная h(x1, ..., хn,k,у). Говорят, что (п + 1)-местная частичная функция f
образуется из функций g и h посредством примитивной рекурсии, если для всех
натуральных значений х1, ..., хn y справедливо:
f(x1, ..., xn,0)=g(x1, ..., xn)
f(x1, ..., xn, y+1)=h(x1, ..., xn, y, f(x1, .., xn, 0)) (1)
Рекурсивные функции.
Слайд 20 Поскольку областью определения функций является множество всех
натуральных чисел, частичная функция
f, удовлетворяющая условиям (1), существует
для каждых частичных функций g и
h и функция эта будет единственной. Условия (1)задают также последовательность определения значений f на различных шагах
рекурсии:
f(x1, ..., xn,0)=g(x1, ..., xn),
f(x1, ..., xn,1)=h(x1, ..., xn, 1, f(x1, ..., xn, n,m)) (2)
Символически примитивная рекурсия обозначается f=R(g,h); в этой записи R
рассматривается как символ двуместной частичной операции, определенной на
множестве всех частичных функций. Из соотношений (2) вытекает, в частности, что
если g и h являются всюду определенными, то и f также является всюду определенной.
Из (2) видно также то важное обстоятельство, что если умеем находить значения
функций g и h, то значения функции f(a1, ..., an, m+1) можно вычислять "механически",
находя последовательно значения на предыдущих шагах.
Рекурсивные функции.
Слайд 21 Частичная функция f(x1, ..., xn) называется примитивно рекурсивной, если ее
можно
получить конечным числом операций суперпозиции и примитивной рекурсии,
исходя лишь из
простейших функций S1, 0n и Inm.Если операции суперпозиции и примитивной рекурсии применить к всюду
определенным функциям, в результате будет получена также всюду определенная
функция. В частности, все примитивно рекурсивные функции всюду определены.
Операция минимизации
Пусть задана некоторая функция f(x,y). Зафиксируем значение х и выясним, при
каком у значение f(x,у)=0. Более сложной оказывается задача отыскания наименьшего
из тех значений у, при которых f(x,y)=0. Поскольку результат решения такой задачи,
очевидно, зависит от х, то и наименьшее у является функцией х. Примем обозначение:
fi(x)=muy[f(x,y)=0]
(читается: "наименьшее у такое, что f(x,y)=0", а muy, называются mu-оператором
или оператором минимизации).
Рекурсивные функции.
Слайд 22Подобным же образом определяется функция многих переменных:
fi(x1, ..., xn)=muy[f(x1, ...,
xn, y)=0]
Для вычисления функции ф можно предложить следующую процедуру:
Вычислим f(x1,
..., xn,0); если значение равно нулю, то полагаем fi(x1, ..., xn)=0. Если f(x1, ..., xm,0)!=0, то переходим к следующему шагу. Вычисляем f(x1, ..., xn,1); если значение равно нулю, то полагаем fi(x1, ..., xn)=1. Если f(x1, ..., xn,0), то переходим к следующему шагу и т.д.
Если окажется, что для всех у функция f(х1, ..., xm,0)!=0 то функция fi{x1...хn)
считается неопределенной.
Частичная функция f(x1,...,xn) называется частично рекурсивной, если ее
можно получить конечным числом операций суперпозиции, примитивной рекурсии и
минимизации, исходя лишь из простейших функций S1, 0n и lnm.
Класс частично рекурсивных функций шире класса примитивно рекурсивных
функций, т.к. все примитивно рекурсивные функции являются всюду определенными, а
среди частично рекурсивных функций встречаются функции не всюду определенные, а
также нигде не определенные.
Рекурсивные функции.
Слайд 23 Понятие частично рекурсивной функции является одним из главных понятий
теории алгоритмов.
Значение его состоит в следующем: с одной стороны, каждая
стандартно заданная
частично рекурсивная функция вычислима путем некоторойпроцедуры механического характера, отвечающей интуитивному представлению об
алгоритмах. С другой стороны, какие бы классы точно очерченных алгоритмов ни
строились, во всех случаях неизменно оказывалось, что вычислимые посредством них
числовые функции являлись частично рекурсивными. Поэтому общепринятой является
научная гипотеза, формулируемая как тезис Черча:
Класс алгоритмически (или машинно-вычислимых частичных числовых
функций) совпадает с классом всех частично рекурсивных функций.
Рекурсивные функции.
Слайд 24 Понятие частично рекурсивной функции научным эквивалентом интуитивного
понятия вычислимой частичной функции.
Тезис
Черча оказался достаточным, чтобы придать необходимую точность
формулировкам алгоритмических проблем и
в ряде случаев сделать возможнымдоказательство их неразрешимости. В силу тезиса Черча вопрос о
вычислимости функции равносилен вопросу о ее рекурсивности.
Рекурсивные функции.
Слайд 25 Общие подходы.
Алгоритмические процессы - это
процессы,
которые может осуществлять определенным образом устроенная машина,
моделирующая тем самым выполнение
отдельных операций человеком.Функционирование такой машины и есть выполнение некоторого алгоритма. Исходя из свойств алгоритма , можно сформулировать общие требования к таким машинам:
характер их функционирования должен быть дискретным, т.е. состоять из отдельных шагов, каждый из которых выполняется только после завершения предыдущего;
действия должны быть детерминированы, т.е. шаги выполняются в строгом порядке, а их результат определяется самим шагом и результатами предыдущих шагов;
Алгоритм как абстрактная машина.
Слайд 26перед началом работы машине предоставляются исходные данные из области определения
алгоритма;
за конечное число шагов работы машины должен быть получен
результат (или информация о том, что считать результатам); машина должна быть универсальной, т.е. такой, чтобы с ее помощью можно было бы выполнить любой алгоритм.
Чем проще структура (т.е. устройство) описанной машины и чем элементарнее ее шаги,
тем больше оснований считать, что ее работа и есть выполнение алгоритма.
Конечность алфавита является очевидным следствием того обстоятельства, что
решение должно быть получено за конечное число шагов. Таким образом, алгоритм
оказывается конечной последовательностью действий, производимых над данными,
представленными с помощью конечного алфавита.
Алгоритм как абстрактная машина.
Слайд 27 Алгоритм - это любая конечная система правил преобразования информации
(данных) над
любым конечным алфавитом.( В. М. Глушков )
Пусть исходные данные из
области определения алгоритма представленыпосредством алфавита А и образуют при этом конечную последовательность знаков
{a1, ..., аn} - такая последовательность называется словом. В результате выполнения
алгоритма сформируется новое слово {b1, ..., bm}, представленное, в общем случае, в
другом алфавите В. В качестве элементарных выделяются следующие операции (шаги):
замена одного знака исходного слова аi,- знаком bi из алфавита В;
удаление знака исходного слова;
добавление к исходному слову знака из алфавита В.
Однако если в алфавиты включен знак, имеющий смысл пустого знака, добавление
которого к слову слева или справа не изменяет этого слова (аналог числового нуля), то
легко видеть, что операция (2) есть ни что иное, как замена а, пустым знаком, а
операция (3) есть замена пустого знака знаком bj.
Алгоритм как абстрактная машина.
Слайд 28 Таким образом, все возможные алфавитные преобразования сводится к операции
(1) -
замене одного знака другим. Именно по этой причине функционирование
абстрактной машины
сводится к тому, что она обозревает символы (т.е. считываети распознает их), записанные в памяти (в этом качестве выступает бесконечная
лента), и в зависимости от своего состояния и того, каков обозреваемый символ,
она заменяет его другим символом; после этого она переходит в новое состояние,
читает следующий символ и т.д. до команды о прекращении работы. Поскольку
подобные машины являются чисто модельным, теоретическим построением, они
получили название абстрактных машин и рассматриваются в качестве одной из
возможных универсальных алгоритмических систем.
Концепция алгоритма как абстрактной машины была выдвинута практически
одновременно (1936 - 1937 гг.) английским математиком Аланом Тьюрингом и его американским
коллегой Эмилем Постом.
Алгоритм как абстрактная машина.
Слайд 29 Алгоритмическая машина Поста
Пост, в отличие от Тьюринга, не пользовался термином
"машина", а
называл свою модель алгоритмической системой.
Абстрактная машина Поста состоит
из бесконечной ленты, разделеннойна равные секции, а также считывающе - записывающей головки. Каждая
секция может быть либо пуста (т.е. в нее ничего не записано), либо заполнена
(отмечена – т.е. в нее записана метка). Вводится понятие состояние ленты как
информация о том, какие секции пусты, а какие отмечены (по-другому:
состояние ленты – это распределение меток по секциям, т.е. это функция,
которая каждому числовому номеру секции ставит в соответствие либо метку,
либо знак "пусто"). Естественно, в процессе работы машины состояние ленты
меняется. Состояние ленты и информация о положении головки
характеризуют состояние машины Поста.
Алгоритм как абстрактная машина.
Слайд 30 Условимся обозначать головку знаком "V" над обозреваемой секцией, а
метку -
знаком "M" внутри секции. Пустая секция никакого знака не содержит.
За один такт (его называют шагом) головка может сдвинуться на одну
секцию вправо или влево и поставить или удалить метку. Работа машины Поста
заключает в переходе от одного состояния машины к другому в соответствии с
заданной программой, которая строится из отдельных команд. Каждая команда
имеет следующую структуру: хКу, где х - номер исполняемой команды; К –
указание о выполняемом действии; у - номер следующей команды {наследника).
Система команд машины включающая шесть действий, представлена в таблице:
Алгоритм как абстрактная машина.
Слайд 31
Алгоритм как абстрактная машина.
Данный перечень должен
быть дополнен следующими условиями: команда <хМу> может быть выполнена только в пустой секции;
команда <хСу> может применяться только к заполненной секции;
номер наследника любой команды (y) должен соответствовать номеру команды, обязательной имеющейся в данной программе.
Если данные условия не выполняются, происходит безрезультатная остановка
машины, т.е. остановка до получения запланированного результата.
Слайд 32 В отличие от этой ситуации, остановка по команде
является
результативной, т.е. она происходит после того, как результат действия
алгоритма получен.
Кроме того, возможна ситуация, когда машина неостанавливается никогда - это происходит, если ни одна из команд не содержит в
качестве последователя номера команды остановки или программа не переходит
к этой команде.
Алгоритм как абстрактная машина.
Слайд 33 Можно показать, что с помощью машины Поста реализуются (хотя и
довольно
громоздко) все арифметические действия над числами в унарной системе счисления.
Алгоритм как абстрактная машина.
Слайд 34 Алгоритмическая машина Тьюринга
Машина Тьюринга состоит из трех частей: ленты, считывающе
- записывающей
головки и логического устройства.
Лента выступает в качестве внешней памяти;
она считается неограниченной(бесконечной) - уже это свидетельствует о том, что машина Тьюринга является
модельным устройством, поскольку ни одно реальное устройство не может
обладать памятью бесконечного размера.
Как и в машине Поста, лента разбита на отдельные ячейки, однако, в
машине Тьюринга неподвижной является головка, а лента передвигается
относительно нее вправо или влево. Другим отличием является то, что она
работает не в двоичном, а некотором произвольном конечном алфавите
А={delta,a1 ... an} - этот алфавит называется внешним. В нем выделяется
специальный символ - delta, называемый пустым знаком - его посылка в какую
либо ячейку стирает тот знак, который до этого там находился, и оставляет
ячейку пустой. В каждую ячейку ленты может быть записан лишь один символ.
Алгоритм как абстрактная машина.
Слайд 35 Информация, хранящаяся на ленте, изображается конечной последовательностью
знаков внешнего алфавита, отличных
от пустого знака.
Головка всегда расположена над одной из ячеек ленты.
Работа происходиттактами (шагами). Система исполняемых головкой команд предельно проста: на
каждом такте она производит замену знака в обозреваемой ячейке аi, знаком aj.
При этом возможны сочетания:
j=i - это означает, что в обозреваемой ячейке знак не изменился;
i!=0, j=0 означает, что хранившийся в ячейке знак заменяется пустым, т.е. стирается;
i=0, j!=0 означает, что пустой знак заменяется непустым (с номером j в алфавите), т.е. производится вставка знака;
i!=j!=0 соответствует замене одного знака другим.
Таким образом, в машине Тьюринга реализуется система предельно простых
команд обработки информации.
Алгоритм как абстрактная машина.
Слайд 36 Эта система команд обработки дополняется также предельно простой
системой команд перемещений
ленты: на ячейку влево, на ячейку вправо и
остаться на месте,
т.е. адрес обозреваемой ячейки в результате выполнениякоманды может либо измениться на 1, либо остаться неизменным.
Алгоритм как абстрактная машина.
Слайд 37 Общее правило, по которому работает машина Тьюринга,
можно представить
следующей записью: qiaj->q`ia`jDk, т.е. после обзора символа аj, головкой
в состоянииqi, в ячейку записывается символ а`,j, головка переходит в состояние q`i а лента
совершает движение Dk. Для каждой комбинации qiaj, имеется ровно одно
правило преобразования (правил нет только для z, поскольку, попав в это состояние,
машина останавливается).
Алгоритм как абстрактная машина.
Слайд 38Это означает, что логический блок реализует функцию,
сопоставляющую каждой паре входных
сигналов да, одну и только одну тройку
выходных q`ia`jDk - она
называется логической функцией машины и обычнопредставляется в виде таблицы (функциональной схемой машины), столбцы которой
обозначаются символами состояний, а строки - знаками внешнего алфавита. Если
знаков внешнего алфавита n, а число состояний ЛУ - m, то, очевидно, общее число
правил преобразования составит m*n.
Конкретная машина Тьюринга задается перечислением элементов множеств А и
Q, а также, логической функцией, которую реализует ЛУ, т.е. набором правил
преобразования. Ясно, что различных множеств A, Q и логических функций может
быть бесконечно много, т.е. и машин Тьюринга также бесконечно много.
Совокупность состояний всех ячеек ленты, состояния ЛУ и положение головки
называется конфигурацией машины.
Алгоритм как абстрактная машина.
Слайд 39В зависимости от начальной конфигурации возможны два варианта развития событий:
после конечного числа тактов машина останавливается по команде остановки; при
этом на ленте оказывается конечная конфигурация, соответствующая выходной информации; остановки не происходит.
В первом случае говорят, что данная машина применима к начальной
информации, во втором - нет. Вся совокупность входных конфигураций, при которых
машина обеспечивает получение результата, образуют класс решаемых задач.
Алгоритм как абстрактная машина.
Слайд 40
Всякий алгоритм может быть задан посредством тьюринговой функциональной
схемой и реализован
в соответствующей машине Тьюринга.
Эта гипотеза получила название тезиса Тьюринга. Как
и тезис Черча, ее нельзядоказать, так как она связывает нестрогое определение понятия алгоритма со строгим
определением машины Тьюринга.
Алгоритм как абстрактная машина.
Слайд 41 Алгоритм задается системой подстановок,
которые указывают, какие замены символов необходимо
производить и в каком
порядке эти подстановки должны следовать. Такой
подход был предложен А. А.Марковым. В начале 50-х годов было введено понятие нормального алгоритма (сам
Марков называл их алгорифмами).
Вновь рассмотрим некоторый алфавит А, содержащий конечное число знаков
(букв). Введем ряд определений:
Слово - это любая конечная последовательность знаков алфавита.
Число символов в слове называется его длиной.
Слово, длина которого равна нулю, называется пустым.
Слово s называется подсловом слова q, если q можно представить в виде q=rst, где r и t - любые слова в том же алфавите (в том числе и пустые).
Теперь можно определить понятие алгоритма (не являющееся строгим):
Нормальные алгоритмы Маркова.
Слайд 42 Алгоритмом в алфавите А называется эффективно вычислимая
функция, областью определения которой
служит какое-либо подмножество
множества всех слов в алфавите А и значениями
которой также являются слова валфавите А.
В алгоритмах Маркова в качестве элементарного шага алгоритма принимается
подстановка одного слова вместо другого. Пусть в алфавите А построено исходное
слово Р, которое содержит подслово Рr (в общем случае таких подслое в исходном
слове может быть несколько), а также имеется некоторое слово Рk в том же алфавите.
Подстановкой называется замена первого по порядку подслова Рr, исходного
слова Р на слово Рk. Обозначается подстановка.
Алгоритм в данной форме представления задается системой подстановок,
которая представляет собой последовательность (список) подстановок. Если в этом
списке имеются подстановки с левыми частями, которые входят в Р, то первая из них
применяется к Р, в результате чего оно переходит в другое слово Р1. К нему вновь
применяется схема подстановок и т.д.
Нормальные алгоритмы Маркова.
Слайд 43Процесс прекращается в двух случаях: либо в списке не нашлось
подстановки с левой
частью, входящей в Рn, либо при получении Рn
была применена последняяподстановка.
Различные нормальные алгоритмы отличаются друг от друга алфавитами и
системами допустимых подстановок. Нормальный алгоритм Маркова можно
рассматривать как стандартную форму для задания любого алгоритма.
Нормальные алгоритмы Маркова.
Слайд 44Различные варианты решения проблемы формулировки точного определения
алгоритма , привели к
построению так называемых абстрактных алгоритмических
систем (их называют также алгоритмическими моделями).
Сопоставление
алгоритмических моделей.
Слайд 45Основные понятия теории алгоритмов – вычислимая
функция и разрешимое множество.
Функция называется
вычислимой, если имеется алгоритм, вычисляющий ее
значение.
Множество называется разрешимым, если имеется
алгоритм, который длялюбого объекта позволяет определить, принадлежит он данному множеству или
нет.
Сопоставление алгоритмических моделей.
Слайд 46Рассмотренный тезис Черча, утверждает, что всякая частично рекурсивная функция
является вычислимой.
Другими словами, если функцию удалось простроить с
помощью суперпозиции, рекурсии
и минимизации из простейших арифметических, тосуществует алгоритм, ее вычисляющий. Далее последовал тезис Тьюринга,
утверждающий, что для всякой вычислимой функции можно построить машину
Тьюринга, которая ее вычисляет. Можно доказать, что алгоритмы Поста также
сводятся к алгоритмам, реализуемых с помощью частично рекурсивных функций.
Сопоставление алгоритмических моделей.
Слайд 47 Также была доказана теорема о сводимости одной алгоритмической модели к
другой,
следствием которой явились утверждения типа: "любую рекурсивную функцию
можно вычислить с
помощью соответствующей машины Тьюринга-" или ".длялюбой задачи, решаемой с помощью машины Тьюринга, существует решающий ее
нормальный алгоритм Маркова". Таким образом, все модели оказываются
эквивалентными, в чем виден глубокий смысл, ибо результат обработки информации,
безусловно, определяется характером функции (алгоритмом) и входными данными, но
не зависит от вида алгоритмической модели.
Сопоставление алгоритмических моделей.
Слайд 48Задача считается алгоритмически неразрешимой, если не существует
машины Тьюринга (или рекурсивной
функции, или нормального алгоритма Маркова),
которая ее решает.
Проблема алгоритмической разрешимости.
Слайд 49В теории алгоритмов к алгоритмически неразрешимой относится "проблема
остановки": можно ли
по описанию алгоритма (Q) и входным данным (х) установить,
завершится ли
выполнение алгоритма результативной остановкой?Неразрешимость проблемы остановки означает, что нельзя создать общий (т.е. пригодный для любой программы) алгоритм отладки программ.
Проблема алгоритмической разрешимости.
Слайд 50 Неразрешимой оказывается и проблема распознавания эквивалентности
алгоритмов: нельзя построить алгоритм, который
для любых двух алгоритмов
(программ) выяснял бы, всегда ли они приводят
к одному и тому же результату илинет.
Алгоритмическая неразрешимость какой-либо задачи в
общей постановке не исключает возможности того, что разрешимы какие-то ее
частные случаи. Справедливо и обратное утверждение: решение частного случая
задачи еще не дает повода считать возможным ее решения в самом общем случае, т.е.
не свидетельствует о ее общей алгоритмической разрешимости. Роль абстрактных
алгоритмических систем в том, что именно они позволяют оценить возможность
нахождения полного (общего) решения некоторого класса задач.
Проблема алгоритмической разрешимости.
Слайд 51 Сложность алгоритма.
Исполнение любого алгоритма требует определенного объема памяти компьютера
для
размещения данных и программы, а также времени центрального процессора по
обработке
этих данных – эти ресурсы ограничены и, следовательно, правомоченвопрос об эффективности их использования.
Под "самым эффективным алгоритмом" понимается алгоритм, обеспечивающий наиболее быстрое получение результата, поскольку в практических ситуациях именно ограничения по времени часто являются доминирующим фактором, определяющим пригодность того или иного алгоритма.
Сложность алгоритма.
Слайд 52Обсуждать будем временную сложность алгоритмов.
Время работы алгоритма удобно выражать в
виде функции от одной
переменной, характеризующей "размер" конкретной задачи, т.е. объем
входныхданных, необходимых для ее решения.
Временная сложность алгоритма - это функция, которая каждой входной
длине слова n ставит в соответствие максимальное (для всех конкретных
однотипных задач длиной n) время, затрачиваемое алгоритмом на ее решение.
Сложность алгоритма.
Слайд 53При этом, безусловно, предполагается, что во всех задачах используется одинаковая
схема
кодирования входных слов.
Различии между полиномиальными и экспоненциальными алгоритмами.
Полиномиальным называется алгоритм,
временная сложность котороговыражается некоторой полиномиальной функцией размера задачи п.
Алгоритмы, временная сложность которых не поддается подобной оценке,
называются экспоненциальными.
Различие между указанными двумя типами алгоритмов становятся особенно
заметными при решении задач большого размера.
Сложность алгоритма.
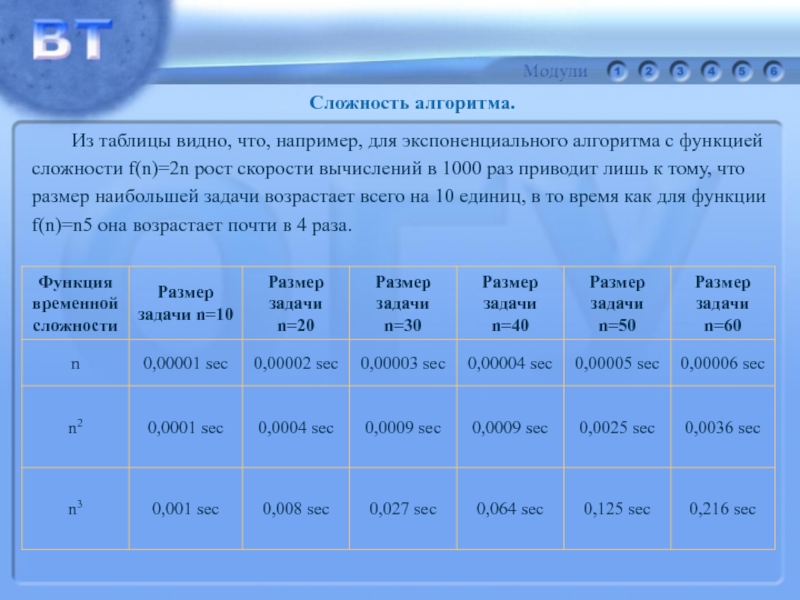
Слайд 54Для сопоставления в таблице ниже приведены данные о времени решения
задач
различной сложности.
Из приведенных данных видно, что, во-первых, время обработки
экспоненциальных алгоритмов
при одинаковых размерах задач (превышающих 20)намного выше, чем у полиномиальных; во-вторых, скорость нарастания времени
обработки с увеличением размера задачи у экспоненциальных алгоритмов
значительно выше, чем у полиномиальных.
Различие между обоими типами алгоритмов проявляются еще более
убедительно, если проанализировать влияние увеличения быстродействия
компьютера на время исполнения алгоритма. В таблице показано, насколько
возрастают размеры наибольшей задачи, решаемой за единицу машинного времени,
если быстродействие компьютера вырастет в 100 и 1000 раз.
Сложность алгоритма.
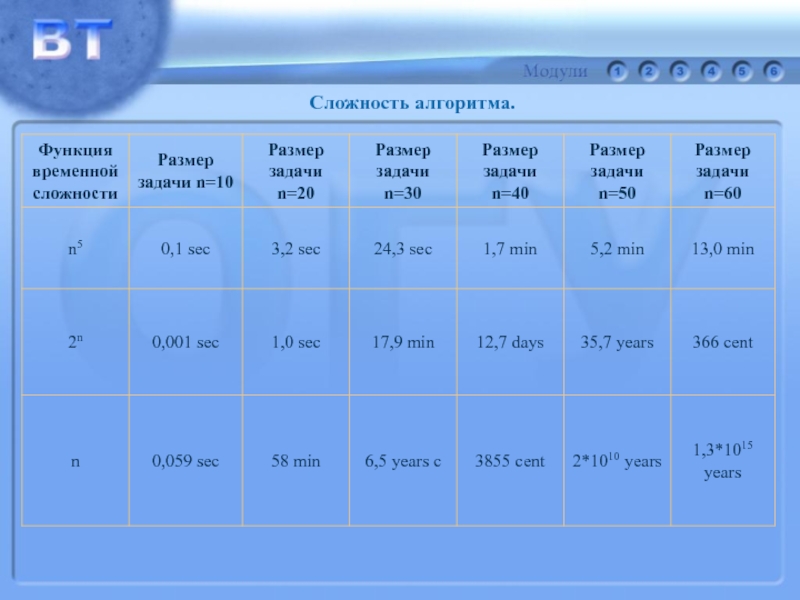
Слайд 55 Из таблицы видно, что, например, для экспоненциального алгоритма с функцией
сложности
f(n)=2n рост скорости вычислений в 1000 раз приводит лишь к
тому, чторазмер наибольшей задачи возрастает всего на 10 единиц, в то время как для функции
f(n)=n5 она возрастает почти в 4 раза.
Сложность алгоритма.
Слайд 57Сложность алгоритма.
Задача считается трудно решаемой,
если для нее не удается построить полиномиального алгоритма. Слайд 58
Формализация представления алгоритмов.
Тема 1: Формальные языки.
Тема
2: Способы представления алгоритмов.Тема 3: Структурная теорема.
Модуль 2.
Слайд 59Формальные языки.
Искусственных язык со строгим синтаксисом и полной смысловой определенностью - такие языки получили название формальный.
В любом языке - естественном или искусственном - можно выделить две составляющие: синтаксис и семантику. Синтаксис (грамматика языка) - это совокупность правил, согласно которым строятся допустимые а данном языке конструкции. Семантика -смысловая сторона языка - она соотносит единицы и конструкции языка с некоторым внешним миром, для описания которого язык используется.
Для описания формального языка необходим другой язык, с помощью которого будут создаваться языковые конструкции. Описываемый формальный язык называется языком-объектом, а язык, средствами которого производится описание - метаязыком.
Слайд 60Формальные языки.
Система правил, позволяющих конструкциям
языка придать смысл - эти правила образуют семантику языка.Формальная грамматика - система правил, описывающая множество конечных последовательностей символов формального алфавита.
Конечные цепочки символов называются предложениями формального языка, а само множество цепочек - языком, описываемым данной грамматикой.
Набор синтаксических правил формального языка аналогичен системе подстановок, используемых в нормальных алгоритмах Маркова.
Слайд 61Формальные языки.
Формальная грамматика задается упорядоченной
четверкой [T, N, S, Р], где T и N - непересекающиеся конечные множества, образующие алфавит или словарь порождаемого формального языка; Т называется множеством (словарем) терминальных символов; N - множеством (словарем) нетерминальных (вспомогательных) символов. S - начальный (выделенный) вспомогательный символ из множества N. Р- набор правил вывода конструкций языка (подстановок) из выделенного вспомогательного символа, имеющие вид g -> h, где g и h - цепочки, состоящие как из терминальных, так и нетерминальных символов.Подстановки работают следующим образом: если в преобразуемой цепочке есть слово g, то оно заменяется словом h. Единственное ограничение на вид подстановок состоит в том, что слово g не может состоять только из терминальных символов. Это означает, что получение на некотором шаге цепочки, состоящей только из терминальных символов, свидетельствует о прекращении процесса порождения - эта цепочка является правильной, завершенной конструкцией порождаемого языка.
Слайд 62Способы представления алгоритмов.
Исполнитель алгоритма
Введем
понятие формального исполнителя:Формальный исполнитель - субъект или устройство, способные воспринимать и анализировать указания алгоритма, изменять в соответствии с ним свое состояние, а также обладающие механизмом исполнения, способным производить пошаговую обработку информации.
Исполнитель алгоритма считается заданным, если для него установлены:
система команд (элементарных действий алгоритма, которые способен выполнить исполнитель);
формы представления входной и выходной информации;
Слайд 63Способы представления алгоритмов.
система допустимых
внутренних состояний; язык представления алгоритма.
Слайд 64Способы представления алгоритмов.
В представлении алгоритмов можно выделить две основные формы: символьную (словесную) и графическую.
Строчная запись, как ясно из названия, представляет собой последовательность строк, каждая из которых содержит описание одного или нескольких элементарных действий. Эти строки могут иметь метки в виде букв или порядковых числовых номеров. Логика алгоритма, т.е. порядок выполнения действий, задается либо в явном виде путем указания метки последующей строки, либо в неявном - по умолчанию управление передается строке, следующей за выполненной.
Слайд 65Способы представления алгоритмов.
"Элементарность" действия определяется возможностями
исполнителя.Данный способ представления алгоритма следует считать основным, поскольку последовательностью строк может быть записана алгоритмическая нотация для любого исполнителя - как человека, так и технического устройства.
Для технического устройства запись производится на специализированном формализованном языке.
Пошагово-словесная форма представляет собой пронумерованную последовательность строк, каждая из которых содержит описания конкретных действий на естественном языке.
Слайд 66Способы представления алгоритмов.
Формула - строчная запись
действий, обеспечивающих обработку числовых, символьных или логических данных. Например, в языке PASCAL для математических и логических операций приняты следующие приоритеты:
операции в скобках;
возведение в степень, вычисление значения стандартных функций и процедур-функций;
логическое отрицание NOT;
умножение, деление, целочисленное деление (div), остаток от целочисленного деления (mod), логическое И (AND);
сложение, вычитание, логическое ИЛИ (OR);
операции отношения (>, <, >=, =, <= >).
Слайд 67Способы представления алгоритмов.
Помимо указанных приоритетов принимается
дополнительное правило: при наличии операций равного приоритета они выполняются в порядке слева направо. Обработка символьной информации производится предназначенными для этого функциями и процедурами.
Псевдокод - ориентированный на исполнителя "человек" частично формализованный язык, позволяющий записывать алгоритмы в форме, весьма близкой к алголоподобным языкам программирования.
Для записи управляющих структур приняты следующие обозначения:
Слайд 68Способы представления алгоритмов.
внешнее оформление:
АЛГ - начало алгоритма, ПРОЦ - начало процедуры, КНЦ; - конец процедуры, КНЦ. - конец алгоритма; ветвление: ЕСЛИ ...ТО...ИНАЧЕ...ВСЕ; после ЕСЛИ ставится описание логического условия, по которому происходит ветвление, после ТО - описание действий (их может быть несколько), которые исполняются при значении условия TRUE, если ветвление полное - после ИНАЧЕ описываются альтернативные действия, в любом случае в конце ставится слово ВСЕ, которое служит признаком окончания данной конструкции;
цикл: ПОКА...ПОВТОРЯТЬ...КЦ; после ПОКА ставится описание логического условия выполнения команд цикла, после ПОВТОРЯТЬ - описание действий (тела цикла), КЦ - признак конца циклической конструкции.
Часто при записи алгоритма отдельные действия заканчиваются разделителем (например, ";"} - это позволяет избежать ошибок в случае, если описание действия занимает не одну строку.
Слайд 69Способы представления алгоритмов.
Язык программирования - искусственный
формализованный язык, предназначенный для записи алгоритма для исполнителя "компьютер", метаязыком которого является естественный язык. Язык программирования строго фиксирует (т.е. определяет) и изображение управляющих структур, и описание допустимых действий, и синтаксические правила построения сложных структур. Различают языки низкого уровня (машинно-ориентированные) и высокого уровня (машинно-независимые). К языкам первого типа относятся:
машинный язык (язык машинных кодов) - совокупность команд, интерпретируемых и исполняемых компьютером; каждый оператор программы на этом языке является машинной командой, а все данные отыскиваются по абсолютным значениям адресов, по которым они располагаются в ОЗУ;
ассемблер (макроассемблер) - язык символического кодирования - операторами языка являются машинные команды, которым приписываются мнемонические обозначения, а в качестве операндов используются не конкретные адреса в ОЗУ, а их символические имена.
Слайд 70 Пример команд ассемблера: CLA - очистить один из регистров сумматора (аккумулятор); ADD
- сложение содержимого ячейки, номер которой написан после команды, с
содержимым аккумулятора; результат остается в аккумуляторе; MOV - содержимое аккумулятора пересылается в ячейку с номером, записаннымвслед за командой; HLT- стоп.
Способы представления алгоритмов.
Слайд 72
Примерами являются язык FORTRAN (FOFtmula TRANsiator) -язык решения сложных научных
и инженерных задач (кстати, это был первый язык программирования высокого
уровня); COBOL {Common Business Oriented Language) - язык для решения экономических и коммерческих задач; LISP {List Processing Language) -язык, используемый в решении задач искусственного интеллекта. К универсальным языкам относятся PASCAL (Philips Automatic Sequence CALcuiator), BASIC {Beginner ALL-purpose Symbolic Instruction Code), С (C++), Jawa, а также современные среды визуального программирования DELPHI, VISUAL BASIC и др.Способы представления алгоритмов.
Слайд 73 Графическая форма записи
Другое распространенное название данной формы - блок-схема. В
данной форме для представления отдельных блоков алгоритма используются обусловленный набор
геометрических фигур. Приняты следующие обозначения:Способы представления алгоритмов.
Слайд 75 Идеи структурного программирования были высказаны в 1965 г. Э. Дейкстрой,
но
сведены в некую законченную систему правил они не были. В
том же годуитальянские математики К. Бом и Д. Джакопини сформулировали теорему о
структурности.
Поскольку алгоритм определяет порядок обработки информации, он должен
содержать, с одной стороны, действия по обработке, а с другой стороны, порядок их
следования, называемым потоком управления.
Часть алгоритма, организованная как простое действие, т.е. имеющая один вход
(выполнение начинается всегда с одного и того же действия) и один выход (т.е.
после завершения данного блока всегда начинает выполняться одно и то же
действие), называется функциональным блоком.
Из этого определения, в частности, следует, что каждое простое действие является
функциональным блоком, а условное - нет.
Согласно положениям структурного программирования можно выделить всего три
различных варианта организации потока управления действиями алгоритма. Поток
управления может обладать следующими свойствами:
Структурная теорема.
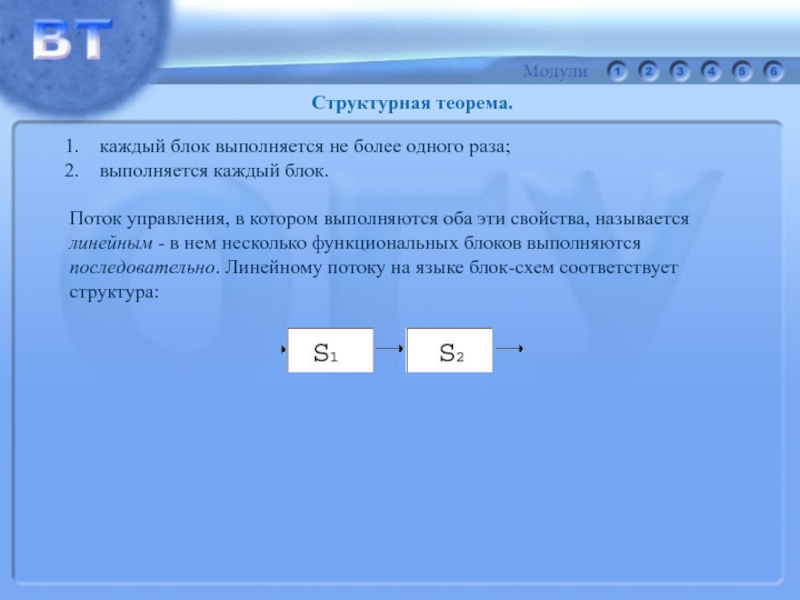
Слайд 76каждый блок выполняется не более одного раза;
выполняется каждый блок.
Поток управления, в котором выполняются оба эти свойства, называется
линейным -
в нем несколько функциональных блоков выполняютсяпоследовательно. Линейному потоку на языке блок-схем соответствует
структура:
Структурная теорема.
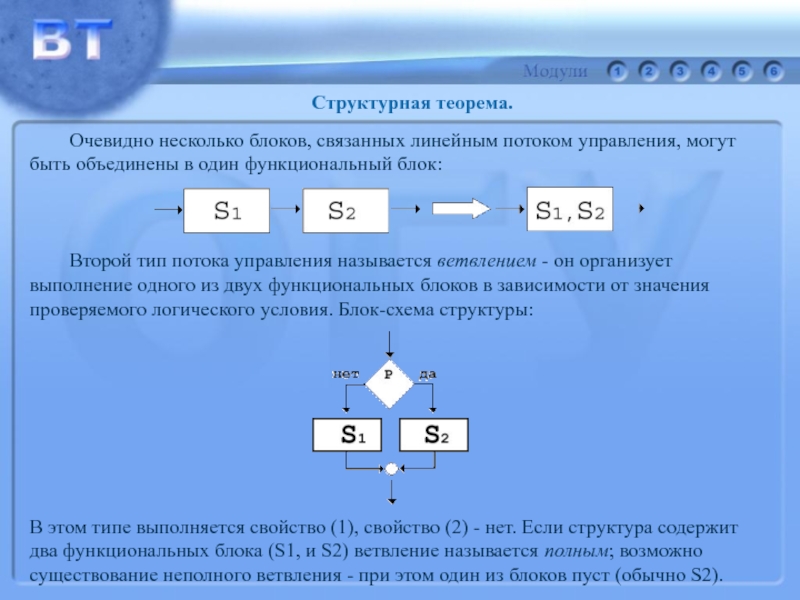
Слайд 77 Очевидно несколько блоков, связанных линейным потоком управления, могут
быть объединены в
один функциональный блок:
Второй тип потока управления называется ветвлением -
он организуетвыполнение одного из двух функциональных блоков в зависимости от значения
проверяемого логического условия. Блок-схема структуры:
В этом типе выполняется свойство (1), свойство (2) - нет. Если структура содержит
два функциональных блока (S1, и S2) ветвление называется полным; возможно
существование неполного ветвления - при этом один из блоков пуст (обычно S2).
Структурная теорема.
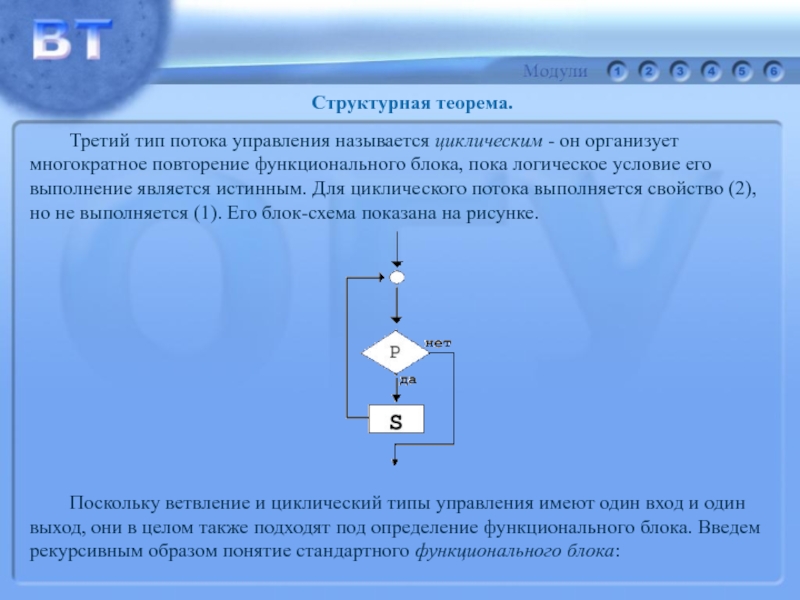
Слайд 78 Третий тип потока управления называется циклическим - он организует
многократное повторение
функционального блока, пока логическое условие его
выполнение является истинным. Для циклического
потока выполняется свойство (2),но не выполняется (1). Его блок-схема показана на рисунке.
Поскольку ветвление и циклический типы управления имеют один вход и один
выход, они в целом также подходят под определение функционального блока. Введем
рекурсивным образом понятие стандартного функционального блока:
Структурная теорема.
Слайд 79Структурная теорема.
каждое простое действие есть стандартный
функциональный блок; каждая из описанных трех управляющих структур является стандартным функциональным блоком, если все входящие в них блоки являются стандартными функциональными;
других стандартных функциональных блоков не существует.
Определим еще одно понятие: Алгоритм называется структурным, если он может быть представлен стандартным функциональным блоком.
Другими словами, структурный алгоритм представляет собой комбинацию трех
рассмотренных выше структур (иногда они называются базовыми алгоритмическими
структурами). Безусловно, не все алгоритмы являются структурными. Однако именно
структурные алгоритмы обладают рядом замечательных преимуществ по сравнению с
неструктурными:
понятность и простота восприятия алгоритма {поскольку невелико число исходных структур, которыми он образован);
проверяемость (для проверки любой из основных структур достаточно убедиться в правильности входящих в нее функциональных блоков);
модифицируемость (она состоит в простоте изменения структуры алгоритма, поскольку составляющие блоки относительно независимы).
Слайд 80Структурная теорема.
После введенных определений можно сформулировать
структурную теорему БомаДжакопини:
любой алгоритм может быть сведен к структурному.
Или по-другому:
любому неструктурному алгоритму может быть построен эквивалентный ему структурный алгоритм.
Значение структурной теоремы для практики программирования состоит в том, что на
ее основе разработан и широко используется структурный метод программирования.
Слайд 81Структурная теорема.
Эффективность метода структурного программирования особенно
заметна присоздании сложных программ; модульный принцип позволяет разбить общую задачу
на составные и относительно автономные части, каждая из которых может
создаваться и отлаживаться независимо (и даже разными разработчиками);
безусловно, такое разбиение требует согласования входных и выходных параметров
модулей.
Слайд 82Литература.
Список используемой и рекомендуемой литературы:
Теоретические основы
информатики: Учебное пособие для вузов. - 2е изд. перераб. и доп. - М.: Горячая линия - Телеком, 2003 - 312 с.; ил. Дайитбегов Д.М., Черноусов Е. А. Основы алгоритмизации и алгоритмические языки. Финансы и статистика. 1992
Игошин В .И. Математическая логика и теория алгоритмов Саратов. Издательство Саратовского университета. 1991
Кузин Л. Т. Основы кибернетики .Том1, 2. М .Энергия 1979
Эдельман С. Л. Математическая логика. М. Наука 1975
Новиков Ф .А. Дискретная математика для программистов. Санкт - Петербург. 2001
Чернов Б.И. Программирование на алгоритмических языках. М. Просвещение.1991





















![Содержание:
Элементы теории алгоритмов.
Формализация представления Подобным же образом определяется функция многих переменных: fi(x1, ..., xn)=muy[f(x1, ..., xn, Подобным же образом определяется функция многих переменных: fi(x1, ..., xn)=muy[f(x1, ..., xn, y)=0]Для вычисления функции ф можно предложить](/img/thumbs/8dd6827460efa078c4857a22e1331e04-800x.jpg)