СОРТИРОВКА

которая на любых двух элементах последовательности принимает одно из трех

значений: меньше, больше или равно.
Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие: ai <= ai+1, для всех i от 0 до n.

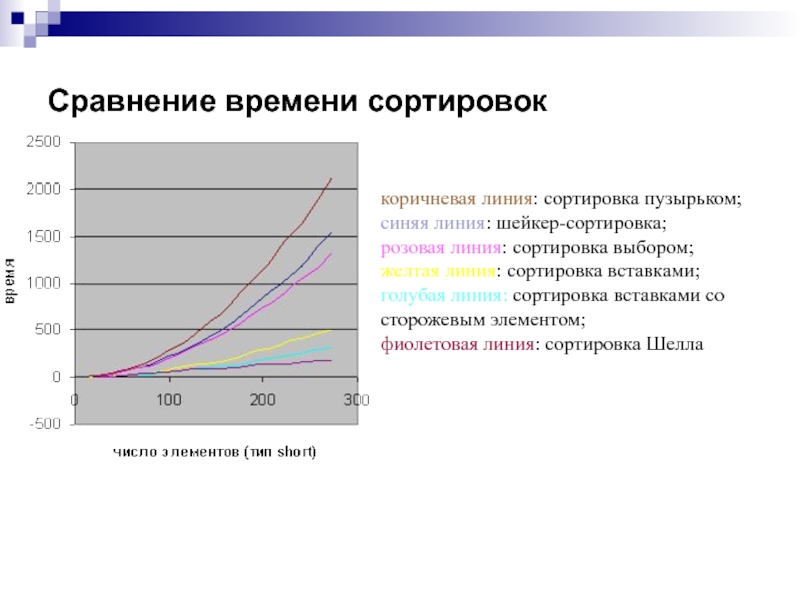
Время сортировки - основной параметр, характеризующий быстродействие алгоритма.
Память - ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы.

Возможна ситуация, когда элементы состоят из нескольких полей:

Если значение функции сравнения зависит только от поля x, то x называют ключом, по которому производится сортировка. На практике, в качестве x часто выступает число, а поле y хранит какие-либо данные, никак не влияющие на работу алгоритма.

Такое свойство может быть очень полезным, если они состоят из

нескольких полей, как на рис. 1, а сортировка происходит по одному из них, например, по x.

Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" осталось прежним: элемент с полем "a", затем - с "b", затем - с "c".

Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" изменилось.

Естественность поведения - эффективность метода при обработке уже отсортированных, или частично отсортированных данных. Алгоритм ведет себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.

и в его начале "вырастает" отсортированная последовательность.

Для i-го шага последовательность разделена на две части:
готовую a[0]...a[i] и неупорядоченную a[i+1]...a[n]. На следующем, (i+1)-м каждом шаге алгоритма берем a[i+1] и вставляем на нужное место в готовую часть массива.
Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним. В зависимости от результата сравнения элемент либо остается на текущем месте(вставка завершена), либо они меняются местами и процесс повторяется.

Таким образом, в процессе вставки мы "просеиваем" элемент x к началу массива, останавливаясь в случае, когда найден элемент, меньший x или достигнуто начало последовательности.

в свою правильную позицию.
При сортировке вставками выполняется меньше перестановок, чем

в пузырьковой сортировке.
Наихудший случай — когда все элементы данных отсортированы в обратном порядке.
Наилучший случай — когда элементы почти отсортированы в правильном порядке.
Сортировка вставками легко реализуется.

вставками проверяются 2 условия. Можно объединить их в одно, поставив

в начало массива специальный сторожевой элемент. Он должен быть заведомо меньше всех остальных элементов массива.

Тогда при j=0 будет заведомо верно a[0] <= x. Цикл остановится на нулевом элементе, что и было целью условия j>=0. Таким образом, сортировка будет происходить правильным образом, а во внутреннем цикле станет на одно сравнение меньше. Однако, отсортированный массив будет не полон, так как из него исчезло первое число. Для окончания сортировки это число следует вернуть назад, а затем вставить в отсортированную последовательность a[1]...a[n].

путем присоединения к ней одного элемента за другим в правильном

порядке. Будем строить готовую последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)-м. На i-м шаге выбираем наименьший из элементов a[i] ... a[n] и меняем его местами с a[i]. Последовательность шагов при n=5 изображена на рисунке ниже.

Вне зависимости от номера текущего шага i, последовательность a[0]...a[i] (выделена курсивом) является упорядоченной. Таким образом, на (n-1)-м шаге вся последовательность, кроме a[n] оказывается отсортированной, а a[n] стоит на последнем месте по праву: все меньшие элементы уже ушли влево.

перестановках.
Всего потребуется n-1 раз выполнить эту последовательность действий.
В

процессе сортировки будет увеличиваться отсортированная часть массива, а не отсортированная, соответственно, уменьшаться.
Общее количество сравнений для сортировки выбором можно вычислить так:
(п-1) + (п-2) + (п-3) +...+ [n-(n-1)] = п(п-1)/2 = п2/2 - п/2 = 0(п2) - это сценарий худшего и лучшего случаев.
Сортировка выбором не учитывает частичной сортировки, которая может существовать в исходных данных.

последнему. Идея метода: шаг сортировки состоит в проходе снизу вверх по

массиву. По пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами.

После нулевого прохода по массиву "вверху" оказывается самый "легкий" элемент - отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента, таким образом второй по величине элемент поднимается на правильную позицию...

Делаем проходы по все уменьшающейся нижней части массива до тех пор, пока в ней не останется только один элемент. На этом сортировка заканчивается, так как последовательность упорядочена по возрастанию.

в свою правильную позицию.
При пузырьковой сортировке сравниваются и переставляются смежные

элементы данных.
Худший случай — когда элементы данных отсортированы в обратном порядке.
Лучший случай — когда элементы данных уже отсортированы в правильном порядке.
Пузырьковая сортировка легко реализуется и не требует дополнительной памяти.

несколько частей, которые сортируются по отдельности и впоследствии "сливаются" в

одну.
Операция слияния:
из каждой части выбирается по одному элементу, и меньший из них помещается в результирующий массив.
так продолжается до тех пор, пока не будет исчерпана одна из частей,
оставшаяся часть просто переносится в конец результирующего массива.

властвуй":
В этом методе фаза разбиения очень простая: она просто

делит список пополам. Фаза слияния более сложная.
На каждом просмотре сортировка слиянием проходит весь список и выполняет O(n) сравнений.
На первом просмотре при сортировке слиянием рассматривается только один список.
На втором просмотре этот алгоритм разбивает список на две половины, а затем сортирует и сливает их.
Поскольку список разбивается пополам, мы получаем не более log2 подсписков для списка из n элементов.
В худшем случае сортировка слиянием имеет производительность порядка nlog2n .

возможно больших расстояниях друг от друга.
Используется рекурсивная реализация сортировки:
Выбрать

элемент данных и сделать его точкой разбиения таким образом, чтобы он разбивал массив на левый и правый подмассивы.






Применить быструю сортировку к левому подмассиву.
Применить быструю сортировку к правому подмассиву.

выборе метода внутренней сортировки.
Этот алгоритм содержит сложную фазу разбиения

и простую фазу слияния.
В лучшем случае выполняется работа порядка nlog2n; в худшем случае выполненная работа эквивалентна работе при сортировке выбором, т.е. O(n2).
Производительность быстрой сортировки сильно зависит от выбора точки разбиения.
Лучше всего быстрая сортировка сортирует массивы, в которых порядок элементов в массиве случаен.

алгоритм сортировки массива a[0].. a[15].
1. Сортируем простыми вставками каждые 8

групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).

2. Сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]). В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.

3. Сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).

4. Сортируем вставками все 16 элементов.

до 1.6n1,25.
Эффективность этого метода сильно зависит от выбора последовательности

значений для h (число разбиений на подмассивы).
Не существует идеальной формулы для выбора этой последовательности, но хорошо подобранные последовательности показывают производительность сортировки по методу Шелла порядка nlog2n.
Сортировка по методу Шелла практически нечувствительна к исходным данным и показывает худшую производительность, чем пузырьковая сортировка и сортировка вставками, когда исходные данные почти отсортированы.
Для случайных наборов данных сортировку Шелла следует рассматривать в числе первых.

сколько элементов, меньших определенного числа,
поместить это число на соответствующие

место.

Особенности алгоритма:
Сортировка подсчетом метод подходит для сортировки целых чисел из не очень большого диапазона.
Этот простой метод не использует вложенных циклов и, учитывая небольшой диапазон значений, время его работы есть O(n).

сортировать числа большего диапазона, используя другую устойчивую сортировку.
Идея состоит в

следующем:
Отсортировать числа по младшему разряду,
Потом устойчивой сортировкой отсортировать по второму, третьему, и так до старшего разряда.
В качестве устойчивой сортировки можно выбрать сортировку подсчетом, в виду малого времени работы.
Время работы всей сортировки есть O(n).
Таким способом можно сортировать не только числа, но и строки, если же использовать сортировку слиянием в качестве устойчивой, то можно сортировать объекты по нескольким полям.

выбором;
желтая линия: сортировка вставками;
голубая линия: сортировка вставками со сторожевым элементом;
фиолетовая

линия: сортировка Шелла