Спектральное представление

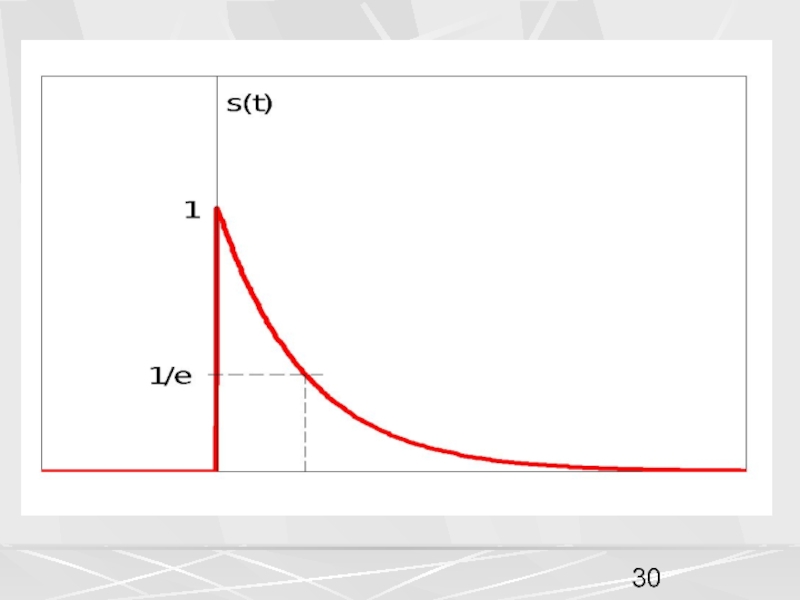
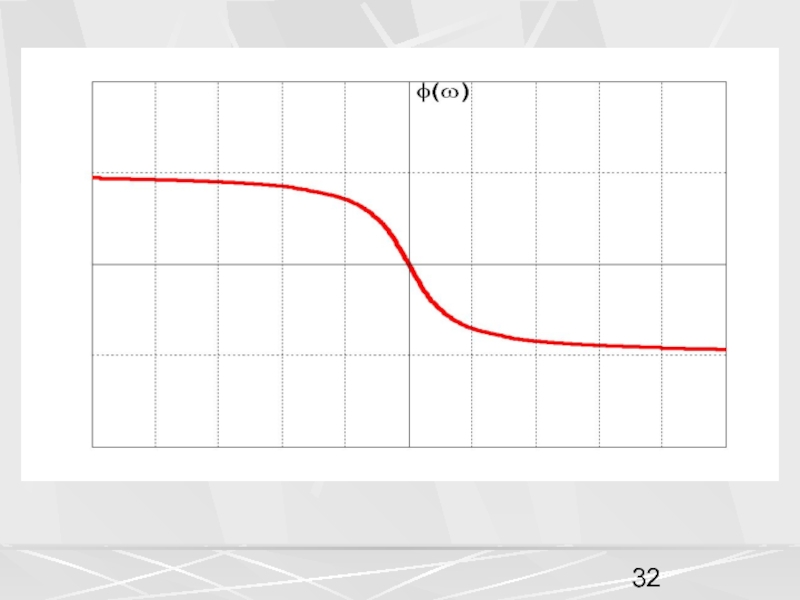
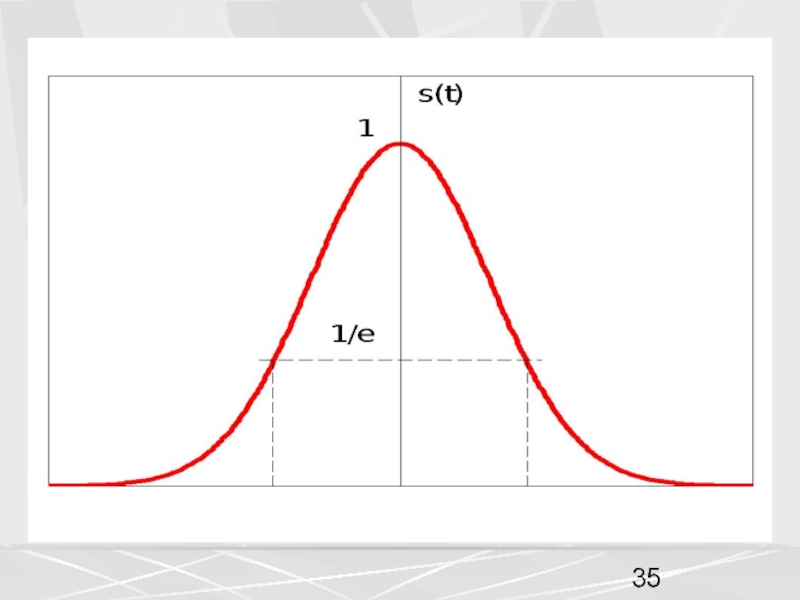
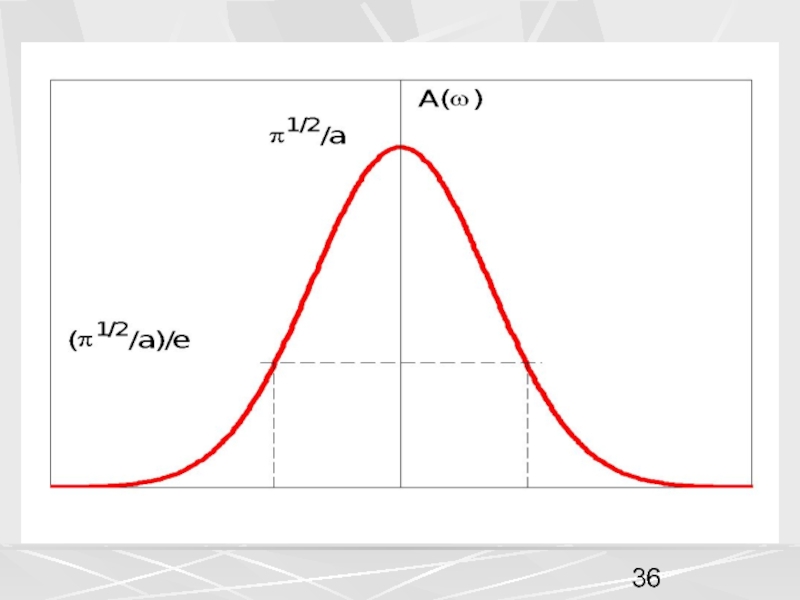
функция времени , при анализе и обработке

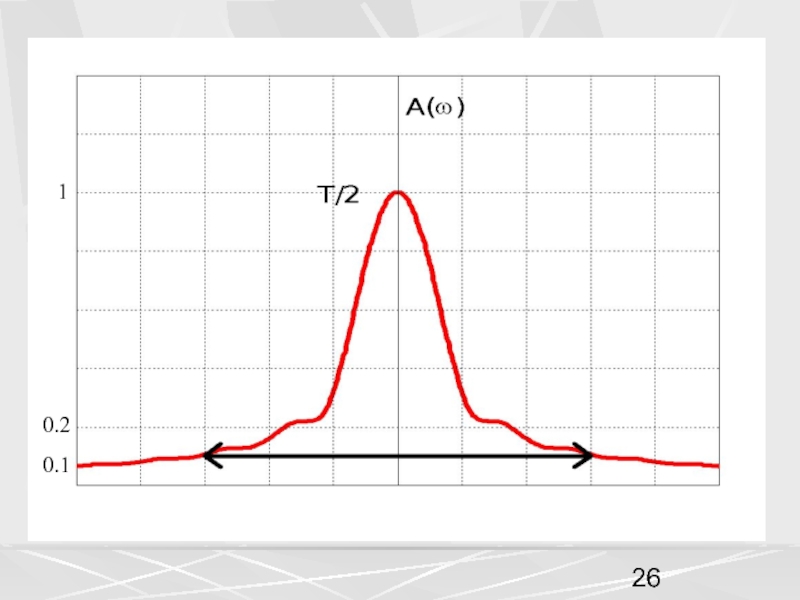
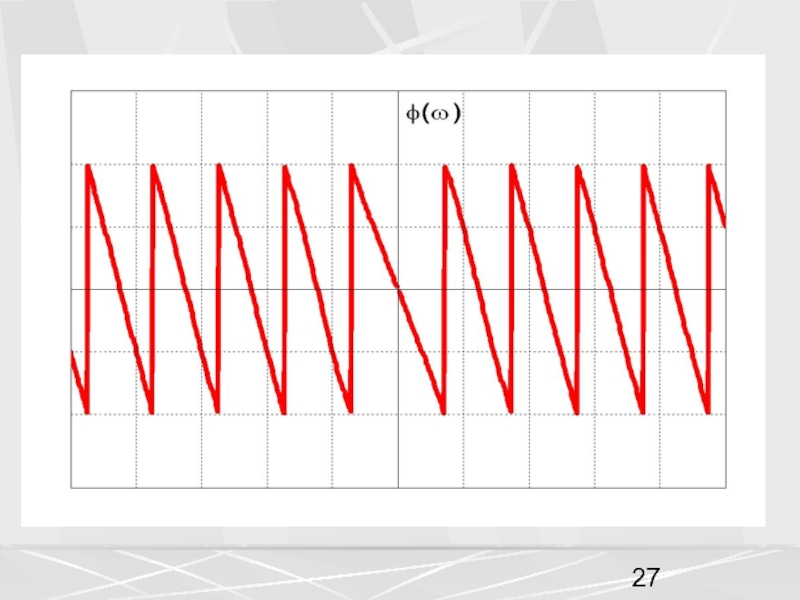
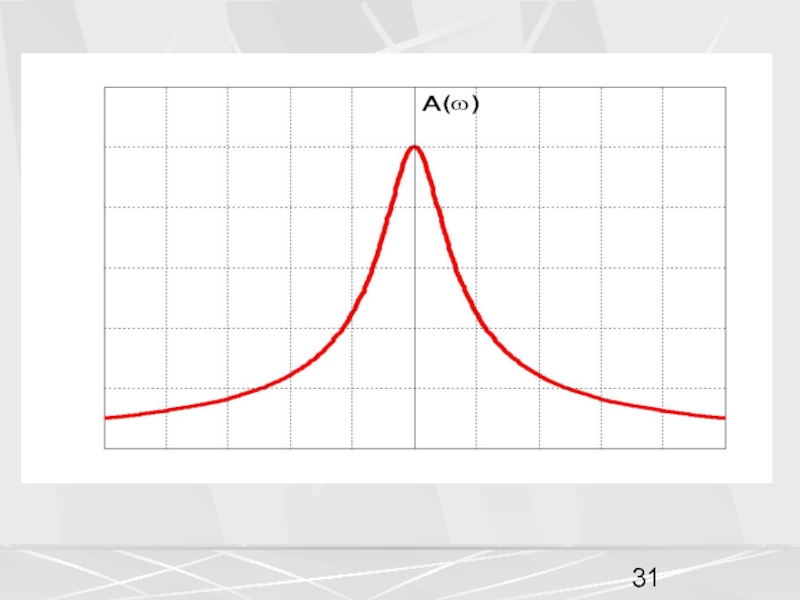
сигналов, используется также частотное представление сигнала в виде функции частоты .
Функции и связаны друг с другом преобразованием Фурье (Fourier transform).

Лекция 2

Спектральное представление сигналов

Здесь первое выражение называется прямое преобразование Фурье (direct Fourier transform), а второе выражение называется обратное преобразование Фурье (inverse Fourier transform).

сигнала ,

(signal spectrum). Имеются также другие названия этой функции – спектральная плотность, спектральная характеристика сигнала.
Функция является комплексной функцией, и может быть представлена в алгебраической и показательной форме. Для простоты записи частоту не указываем

Из теории комплексных чисел известно, что и действительные и мнимые части комплексного числа , и обозначаются

аргументом комплексного числа . Действительная и мнимая части комплексного числа могут быть выражены через модуль и аргумент комплексного числа следующими соотношениями

Соответственно, модуль и аргумент комплексного числа выражаются через действительную и мнимую части комплексного числа. Эти выражения имеют вид:

, а обычную , то формулы прямого и

обратного преобразования Фурье становятся более симметричными.

Из спектра можно получить амплитудно-частотную характеристику (АЧХ) и фазово-частотную характеристику (ФЧХ) сигнала (amplitude-frequency, phase-frequency characteristic), с помощью соотношений.

сложный сигнал можно представить в виде суммы

(или интеграла) более простых (базисных) сигналов

Обратим внимание на обратное преобразование Фурье

с весовыми множителями:

Формула Эйлера связывает эти простые сигналы с гармоническими колебаниями.

по гармоническим колебаниям.
Кроме разложения по гармоническим

функциям применяются и другие типы разложения: по функциям Уолша, Бесселя, Хаара, полиномам Чебышева, Ляггера, Лежандра и др.
В радиотехнике в качестве базисных функций разложения Фурье используют преимущественно гармонические функции. Это объясняется следующими причинами.
1) Гармоническое колебание сохраняют свою форму при прохождении через линейный преобразователь. Изменяться лишь амплитуда и фаза.
2) Для гармонических функций имеется мощный математический аппарат.
3) Гармоническое колебание легко осуществить на практике.

лекции. Сейчас же мы отметим только некоторые из этих свойств.

Первое, если сигнал вещественная функция, то для спектра выполняются следующие соотношения четности

Здесь звездочка означает комплексное сопряжение. Из этих соотношений видно, что для вещественного сигнала, АЧХ - четная функция, а ФЧХ – нечетная функция.

для спектра выполняются следующие соотношения

Третье, если сигнал

вещественная нечетная функция времени

то для спектра выполняются следующие соотношения

Фурье
Примеры спектров некоторых сигналов
Прямоугольный импульс
Рассмотрим прямоугольный импульс,

центрированный относительно начала отсчета времени и имеющий длительность .

что рассматриваемый прямоугольный импульс является действительной четной функцией времени.

затухая. Поэтому вводят понятие эффективной ширины спектра.
Как

видно из графиков, спектр имеет лепестковый характер и ширина главного лепестка равна

При лепестковом характере спектра за эффективную ширину спектра принимают ширину главного лепестка. Длительность прямоугольного импульса равна

равна некоторому числу (это произведение называется базой сигнала).

В случае прямоугольного импульса это есть:

Это означает, что чем короче сигнал, тем шире его спектр и наоборот. Например

соотношению неопределенности, гласящему, что произведение этих параметров не может быть

меньше единицы.

Отсюда следует:
1) Можно сформировать сигнал большой длительности, одновременно имеющий широкий спектр. Такие сигналы называют широкополосными, или сложными, или сигналами с большой базой.
2) Короткий сигнал с узким спектром существовать не может.

после сдвига прямоугольного импульса во времени. Пусть импульс начинается в

нулевой момент времени.

Вычисляем спектр с помощью прямого преобразования Фурье

друг друга иллюстрирует общее свойство – АЧХ не меняется, меняется

только ФЧХ.

Фурье. Если сравнить формулы прямого и обратного преобразования Фурье, можно

заметить, что они отличаются друг от друга лишь знаком в показателе комплексной экспоненты и множителем перед интегралом.
Отсюда следует, что если функции времени соответствует спектральная функция , то функции времени будет соответствовать спектральная функция .
Другими словами формы сигнала и его спектра поменяются местами.

с помощью прямого преобразования Фурье
Продемонстрируем это на

примере прямоугольного импульса. Рассмотрим сигнал следующего вида

Следующие рисунки показывают импульс и его спектр.

Фурье
Несимметричный треугольный импульс
Рассмотрим несимметричный треугольный импульс.


Следующие

рисунки показывают несимметричный треугольный импульс и его АЧХ и ФЧХ

выраженных лепестков, поэтому для определения эффективной ширины спектра необходим иной

критерий. Будем определять эффективную ширину спектра по уровню 0.1 от максимума. Из графика видно, что эта ширина (она показана стрелкой) составляет примерно

Так как длительность треугольного сигнала равна

,

то база треугольного сигнала равна

с помощью прямого преобразования Фурье
Односторонний

экспоненциальный импульс

У рассмотренных импульсов ФЧХ имела резкий пилообразный характер. Мы рассмотрим сейчас импульс, у которого ФЧХ имеет гладкую зависимость. Рассмотрим односторонний экспоненциальный импульс

0.1 от максимума. Из графика видно, что эта ширина составляет

примерно

Для экспоненциальных сигналов в качестве длительности сигнала обычно берется время, при котором амплитуда сигнала убывает в раз. Поэтому длительность экспоненциального сигнала равна

Таким образом, база экспоненциального сигнала равна

с помощью прямого преобразования Фурье


Поскольку сигнал является

четной действительной функцией, его спектр получился чисто вещественной функцией, кроме того положительной функцией. Это означает, что амплитудно-частотная характеристика АЧХ совпадает со спектральной функцией. Фазово-частотная характеристика ФЧХ в этом случае просто равна нулю.

спектр также описывается гауссовой функцией.
Определим его

эффективную длительность и ширину спектра по уровню от максимума. Тогда получим

База гауссова сигнала, таким образом, равна четырем

произвольной природы, для которых определены операции сложения и умножения на

скаляр, удовлетворяющие следующим аксиомам:

пространством (ЛНП), если каждому элементу , поставлено в соответствие число

.
Это число называется нормой элемента, и удовлетворяет следующим аксиомам (аксиомам нормы).

определить разными способами. Для задач ЦОС наиболее подходит норма, определенная

следующим образом:

Квадрат такой нормы будем называть энергией сигнала.

ЛНП с конечной нормой называется пространством функций с интегрируемым квадратом, и обозначается .

элементов поставлено в соответствие

неотрицательное число , называемое метрикой (расстоянием), удовлетворяющее следующим аксиомам (аксиомам метрики).

Обычно метрику вводят следующим образом:

элементов поставлено в соответствие вещественное число

, называемое скалярным произведением, удовлетворяющее следующим аксиомам:

в себе все свои предельные точки.

Евклидово пространство,

полное с нормой

называется гильбертовым пространством.