Слайд 2Что такое деньги?
Деньгами экономисты называют любые активы, которые используются в
качестве средства платеже при осуществлении сделок.
Этапы развития денег как средства
облуживания товарного обмена:
бартер;
товарные деньги;
металлические деньги;
бумажные деньги;
кредитные деньги;
электронные деньги.
Слайд 4Все финансовые активы подразделяют по степени ликвидности
Абсолютной ликвидностью обладают наличные
деньги (банкноты и монеты в обращении), т.к. принимаются к оплате
без всяких ограничений. Они образуют денежный агрегат М0.
В агрегат, М1, кроме нал. денег включают чековые депозиты и вклады до востребования. В макроэкономике под агрегатом М1 понимают деньги в узком смысле.
В агрегат, М2, помимо М1 включают срочные вклады, которые могут быть получены обратно без уведомления.
В агрегат М3 помимо М2 входят крупные срочные вклады, изъятие которых возможно лишь после предварительного уведомления, а также другие счета в небанковских финансовых институтах.
Слайд 5Функции денег
Средство обращения - при проведении сделок по покупке или
продаже товаров и услуг.
Счетная единица или мера измерения стоимости –
т.к. стоимость всех товаров и услуг выражается в денежных единицах.
Слайд 6Деньги позволяют перераспределять ресурсы во времени – т.о., деньги также
служат средством сохранения стоимости (или средством накопления).
Средство платежа - при
выплате заработной платы или при предоставлении и погашении кредитов.
Мировые деньги - для обслуживания мирохозяйственных связей стран приводит к появлению функции.
Слайд 7Трансакционный спрос на деньги: модель Баумоля- Тобина
ТС на деньги возникает
из-за необходимости использовать деньги для совершения регулярных платежей.
Слайд 8Предположения:
Доход перечисляется на банковский счет индивида,
на остаток средств ежемесячно начисляются
проценты.
Слайд 9Потребитель может:
- Снять деньги со счета и потерять проценты.
-
Посещать банк и снимать деньги только тогда, когда они ему
нужны.
Тогда остаток на счете и, процентные начисления будут выше.
Однако появляются неудобства, связанные с частыми посещениями банка.
Это приведет к дополнительным затратам времени и денег.
Слайд 10Т.О., задача потребителя
состоит в том, чтобы
выбрать оптимальную
стратегию снятия денег
со счета
с учетом
возможных упущенных
процентных платежей, и
дополнительных
трансакционных издержек.
Слайд 11Поведение условного потребителя.
Номинальный доход индивида
YN = Y*P,
где Y - реальный
доход.
Он имеет сберегательный счет, на который ежемесячно начисляются процентные платежи
и номинальная ставка процента равна i.
Примем, что трансакционные издержки не зависят от того, какая сумма снимается со счета и обозначим tc.
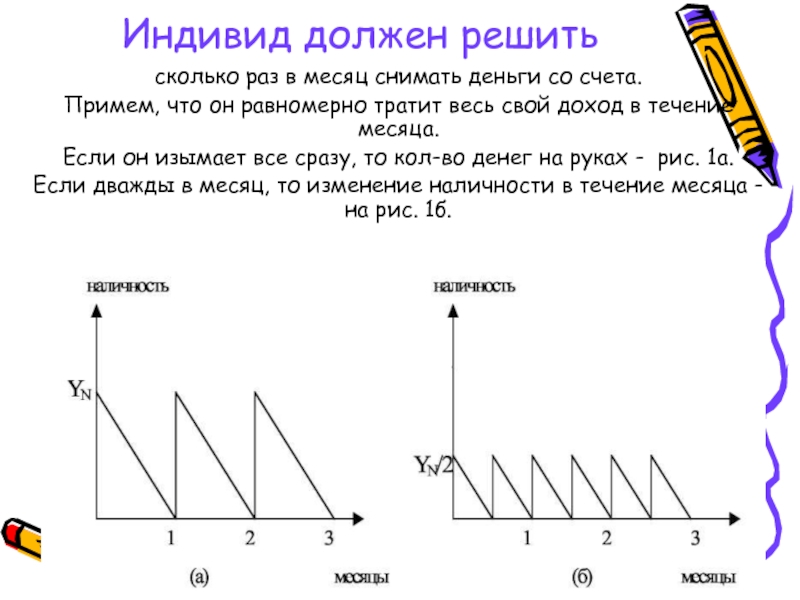
Слайд 12Индивид должен решить
сколько раз в месяц снимать деньги со счета.
Примем,
что он равномерно тратит весь свой доход в течение месяца.
Если
он изымает все сразу, то кол-во денег на руках - рис. 1а.
Если дважды в месяц, то изменение наличности в течение месяца - на рис. 1б.
Слайд 13Обозначим:
n - количество изъятий денег в банке в течение месяца;
YN/n
- сумма, которую каждый раз снимает индивидуум;
YN/2n - среднее количество
денег на руках в течение периода.
Тогда величина упущенных процентов за период равна
i*YN/2n,
а общие трансакционные изджержки
tc*n
Совокупные издержки составят
(tc*n + i*YN/2n).
Слайд 14Тогда задача потребителя состоит в том,
чтобы выбрать n,
минимизируя совокупные издержки:
Тогда
оптимальное число походов в банк:
Слайд 15Оптимальная средняя величина наличности:
Слайд 16Примечание:
Из модели следует, что реальный спрос на
деньги не зависит от
уровня цен.
Если цены выросли на 10%, то YN и номинальная
величина tc также возросла на
10%, что означает увеличение
номинального денежного спроса на 10%,
значит реальный спрос (M/P) остается неизменным.
Слайд 17Свойства функции трансакционного спроса
- Спрос на деньги отрицательно зависит от
номинальной ставки процента.
Потому, что повышение процентной ставки ведет к
росту
упущенных процентных платежей и
побуждает индивидуума чаще ходить в банк и
держать меньшее количество наличных средств.
Рост реального дохода положительно влияет на
реальные денежные балансы.
Слайд 18Однако рост дохода на 10% не приведет к такому же
увеличению спроса на деньги
то есть, при повышении дохода индивид находит
выгодным не увеличивать количество визитов в банк пропорционально изменению доходов.
Потому, что транс. издержки не зависят от снимаемой суммы, а пропорциональны числу визитов, поэтому
агент с более высоким доходом пользуется экономией
на масштабе, одновременно увеличивая не только
число визитов, но и размер снимаемой суммы.
Тогда эластичность спроса на деньги по реальному
доходу:
Слайд 19Примечание:
При условии целочисленности n* эластичность по доходу будет между 1/2
и 1,
т.к. возможна ситуация,
когда рост дохода не
приведет к изменению
числа визитов
в банк, а
повлияет лишь на
среднюю величину
наличности.
Слайд 21Можно выделить еще
параметр, который оказывает влияние на желаемую величину реальных
денежных балансов.
Слайд 22Это трансакционные издержки.
Их рост делает невыгодным частое
посещение банка, и приводит
к увеличению
среднего кол-ва денег на руках, т.е., к росту
трансакционного спроса
на деньги.
Т.О., мы можем представить в общем виде функцию трансакционного спроса:
Слайд 23Спрос на деньги, вызванный осторожностью.
Слайд 24Модель трансакционного
спроса БТ не принимает во
внимание проблему
неопределенности, когда
индивид может испытывать
затруднения,
связанные с
отсутствием денег.
Примем, что издержки,
связанные с отсутствием
ликвидных средств
можно
выразить в деньгах
и обозначим их q.
Слайд 25Вероятность возникновения такой ситуации
зависит от того, сколько средств индивидуум в
среднем держит в ликвидной форме и, какова степень неопределенности относительно
доходов и расходов.
Чем больше у индивидуума наличных денег и, чем меньше степень неопределенности, тем меньше вероятность неплатежеспособности.
Слайд 26С другой стороны
храня средства в наличной форме, он лишается процентов,
которые мог бы получить, положив эти средства на депозит.
Оптимальное количество
денег на руках
должно уравновешивать предельные
издержки, связанные с недополученными
процентами с предельной выгодой от
сокращения издержек, связанных с
неплатежеспособностью.
Слайд 27Введем обозначения:
M - средняя величина наличности;
i - ставка банковского процента.
Тогда
издержки, связанные с упущенными процентными платежами - iM.
Вероятность столкновения
с ситуацией
отсутствия ликвидных средств p(M, σ)
отрицательно зависит от имеющейся
наличности M и положительно от степени
неопределенности σ.
Слайд 28Агент, нейтральный к риску,
выбирает оптимальный уровень
наличности M*, минимизируя совокупные
ожидаемые издержки:
Слайд 30Условие первого порядка:
В левой части - предельные издержки, связанные с
упущенными процентными платежами,
В правой - предельная выгода от снижения издержек,
вызванных неплатежеспособностью.
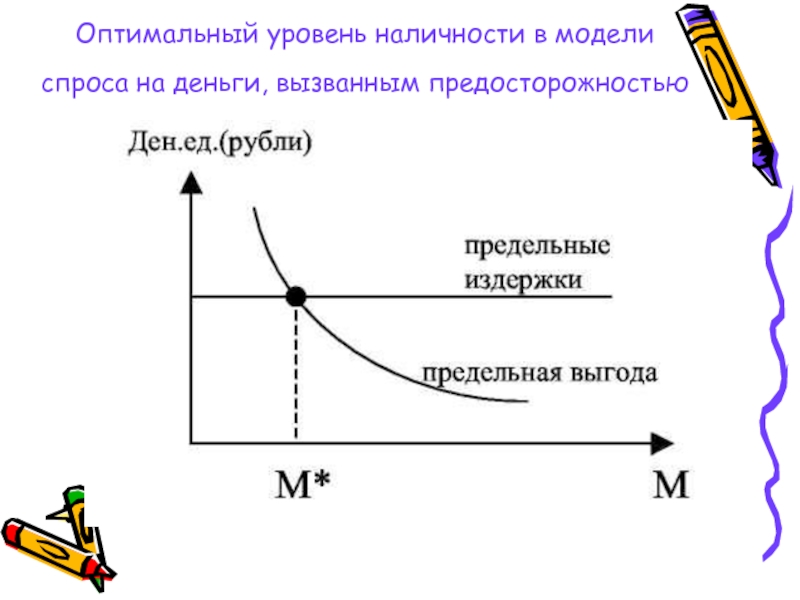
Слайд 31Оптимальный уровень наличности в модели спроса на деньги, вызванным предосторожностью
Слайд 32Почему так?
Предполагая, что предельная выгода от
снижения издержек, связанных с
неплатежеспособностью,
является
убывающей функцией наличных денег,
мы можем изобразить кривую предельной
выгоды и линию
предельных издержек,
точка пересечения которых дает
оптимальную величину наличности M*.
Слайд 33Проанализируем, какие факторы и как
влияют на величину спроса на деньги
из предосторожности.
Ставка процента i.
Рост ставки процента сдвигает вверх кривую предельных
издержек, что ведет к сокращению оптимальной величины наличности.
Величина потерь, связанных с неплатежеспособностью, q
Если q растет, то это вызывает сдвиг вверх кривой предельной выгоды, что ведет к росту оптимальной величины наличности.
Слайд 34Уровень неопределенности также влияет на M*.
Считая, что рост σ приводит
к сдвигу вверх кривой предельной выгоды, получаем, что увеличение уровня
неопределенности влечет рост спроса на деньги из предосторожности.
Т.О., можно записать параметры, влияющие на спрос на деньги из предосторожности:
Слайд 35Спекулятивный спрос на деньги.
Трансакционный спрос и спрос, вызванный предосторожностью
относятся к
функции денег как средства обращения,
так как индивид держал деньги
для оплаты.
Спекулятивный спрос на деньги объясняет поведение
агрегата М2, в то время как
предыдущие относятся скорее к М1.
Слайд 36Какими критериями руководствуется индивидуум
когда использует деньги как средство сохранения стоимости?
Деньги
по сравнению с другими фин. активами приносят значительно меньший доход.
Слайд 37С другой стороны, доходность является случайной величиной и для более
высокодоходных
активов наблюдается
больший разброс доходностей, то есть
больший риск.
Слайд 38Если индивид не склонен к риску, то он
диверсифицирует вложения и
часть богатства
хранит в виде денег, а часть - в виде
рисковых ФА.
Слайд 39Рассмотрим простейшую модель выбора оптимального портфеля ФА.
Разделим все ФА на
две группы.
Безрисковые активы – с очень низкой ожидаемой доходностью (назовем
их деньгами).
2. Альтернативные активы – с большей доходностью и большим риском:
Слайд 40Введем обозначения:
_
- Ожидаемая доходность - r,
- а риск (как среднеквадратическое отклонение) - σ
Тогда характеристика первого первого актива (денег):
_
rM ≥ 1, σM = 0.
Для второго актива:
_ _
rА > rM, σA > 0.
Слайд 41Если α (0≤α≤1) - доля вложений в безрисковый актив (деньги),
тогда
доля вложений в альтернативный актив - (1-α).
Если W- богатство индивида,
то вложения в безрисковый актив будут равны α×W.
Слайд 42Индивидуум не склонен к риску, тогда
чем выше риск (при прочих
равных), тем ниже уровень ожидаемой полезности.
Примем, что ожидаемая полезность зависит
от ожидаемой доходности портфеля положительно и от риска портфеля отрицательно:
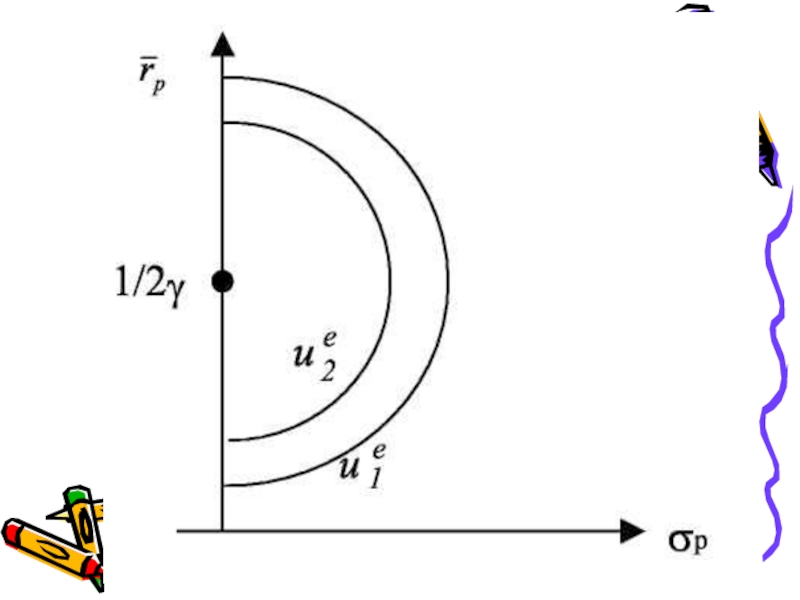
Слайд 43можно изобразить линии уровня этой функции в пространстве риск -ожидаемая
доходность.
Эти линии представляют из себя окружности
с центром в точке
Слайд 45Далее будем считать,
что все активы имеют ожидаемые доходности, лежащие ниже
точки насыщения:
_
rA < 1/2γ.
Слайд 46Если xi - случайная величина,
соответствующая валовой доходности актива i.
Тогда
ожидаемая валовая доходность портфеля равна:
Слайд 47Вывод:
ожидаемая доходность портфеля
равна средневзвешенной величине
ожидаемых доходностей входящих в
портфель активов.
Слайд 48Теперь определим риск портфеля
который равен квадратному корню из дисперсии (Var).
Дисперсия портфеля :
Слайд 49Учитывая, что
Var(xM) = σ2M = 0,
Var(xA) = σ2A
и
Cov(xM,xA) = 0
то:
σ2p = (1−α)2σ2A.
Слайд 50Тогда ожидаемая доходность и риск портфеля равны:
Откуда:
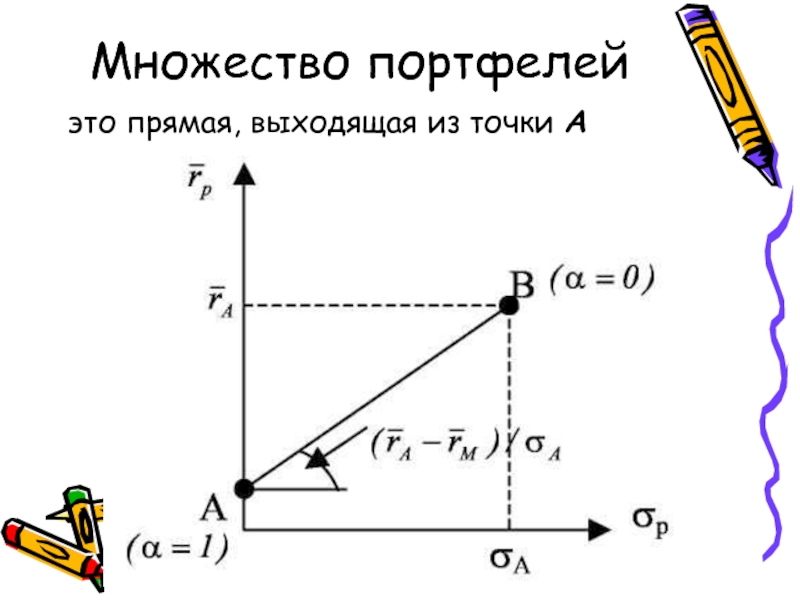
Слайд 51Множество портфелей
это прямая, выходящая из точки А
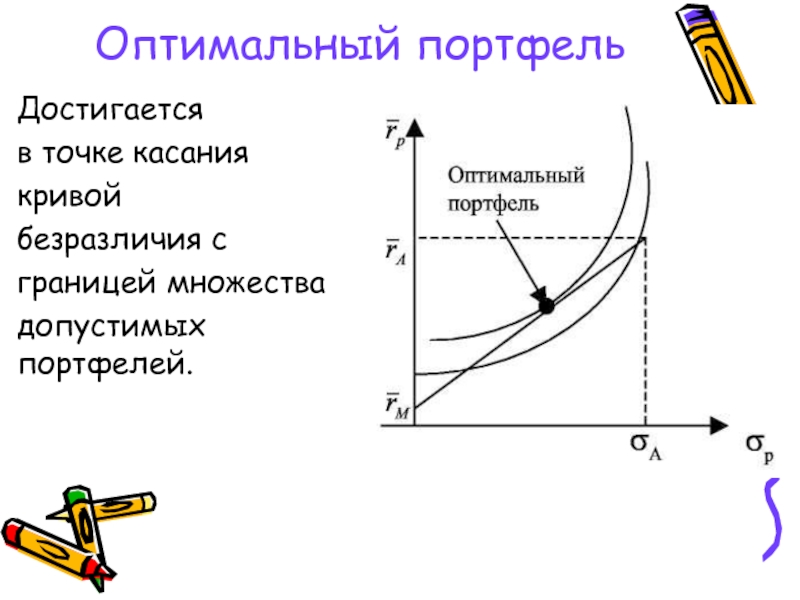
Слайд 52Оптимальный портфель
Достигается
в точке касания
кривой
безразличия с
границей множества
допустимых портфелей.
Слайд 53Какие факторы влияют на наше решение об оптимальном распределении богатства?
ожидаемая
доходность
риск альтернативных активов
величина богатства также влияет на сумму вложений
в каждый из активов.
Тогда задача выбора оптимального портфеля:
Слайд 54Тогда функция спекулятивного денежного спроса:
где rM- собственная доходность денег,
_
rА -
ожидаемая доходность альтернативного актива,
σА - риск по альтернативному активу,
W
- реальное богатство.
Слайд 55Спрос на деньги при гиперинфляции (функция Кейгана).
Учитывает тот факт, что
существуют еще физические активы,
которые могут рассматриваться как альтернатива деньгам.
Это актуально
в условиях высокой инфляции, т.к. деньги и
другие фин. активы очень быстро обесцениваются и
потребители стараются от них избавиться.
Слайд 57Сопоставляя доходность от хранения денег с доходностью физ. активов,
получаем,
что альтернативная стоимость хранения
денег равна реальной доходности физических активов
с поправкой
на ожидаемую инфляцию.
Слайд 58Учитывая, что
в условиях высокой инфляции изменения реальной доходности физ.
активов незначительны
по сравнению
с изменением уровня инфляции,
а также полагая неизменным реальный
доход,
Филипп Кейган предложил
Слайд 59рассматривать
спрос на деньги как функцию ожидаемой инфляции,
которая получила название
функции Кейгана:
M/Р = f(πexp) = е- γπexp , где
πexp
- ожидаемая инфляция и γ>0.
Слайд 60Скорость обращения денег
и количественная теория денег.
скорость обращения денег (V)
-
как отношение совокупных расходов к реальным денежным балансам:
Слайд 61Спрос на деньги является функцией дохода и ставки процента, поэтому:
Т.о.,
V положительно зависит от ставки процента.
Влияние реального дохода зависит от
эластичности
спроса на деньги по доходу и также характеризуется
положительной зависимостью между V и доходом.
Слайд 62Тогда можно записать:
M×V = P×Y.
Уравнение, связывающее уровень
цен, выпуск, скорость обращения
и
денежную массу, называют
уравнением количественной
теории денег
(уравнением обмена).
Слайд 63Прямым следствием из уравнения
КТД является
постулат о нейтральности денег.
Т.е при
постоянстве V и
полной занятости кредитно-денежная
политика является нейтральной по
отношению ко всем
реальным
переменным, воздействуя только на
номинальные переменные (уровень цен).