Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сравнение и корреляция
Содержание
- 1. Сравнение и корреляция
- 2. Содержание лекции 1. Задача сопоставления данных: эквивалентность,
- 3. Задача сопоставления данных Статистические оценки степенисвязи Метрические
- 4. Преобразования и эквивалентность Примеры отношений эквивалентности:
- 5. Преобразования и эквивалентность Разбиение множества — это представление
- 6. Преобразования и эквивалентность 2D-преобразования: сдвигКласс квадратов заданного размераКласс кругов заданного размера
- 7. Преобразования и эквивалентность 2D-преобразования: сдвиг, поворотКласс квадратных ромбов одного размераКласс кругов одного размера
- 8. Преобразования и эквивалентность 2D-преобразования: сдвиг, масштаб, поворотКласс всех квадратных ромбовКласс всех кругов
- 9. Преобразования и эквивалентность 2D-преобразования: сдвиг, масштаб, поворотКласс всех квадратных ромбовКласс всех кругов
- 10. Напоминание: двумерные аффинные преобразования
- 11. Преобразования и эквивалентность 2D-преобразования: аффинные преобразованияКласс параллелограммовКласс эллипсов
- 12. Преобразования и эквивалентность 2D-преобразования: проективные преобразованияКласс выпуклых четырехугольниковКласс эллипсов
- 13. Преобразования и инварианты Инвариант — это свойство
- 14. Признаковое описание изображений Геометрическое описание выделенных областейЧасто
- 15. Признаковое описание изображений Геометрическое описание выделенных областейКоординаты
- 16. Признаковое описание изображений Геометрическое описание выделенных областейДля
- 17. Признаковое описание изображений Геометрическое описание выделенных областейПериметр
- 18. Признаковое описание изображений Топологические признаки(геометрические инварианты):число несвязных
- 19. Признаковое описание изображений Инвариантные моментымоменты, инвариантные к
- 20. Сопоставление данных как оценка степени связи и
- 21. Статистическая корреляцияКорреляция (корреляционная зависимость) — статистическая взаимосвязь двух или
- 22. КовариацияКовариация (или корреляционный момент) является совместным центральным
- 23. Коэффициент корреляцииЛинейный коэффициент корреляцииСвойства коэффициента корреляции ,
- 24. Коэффициент корреляцииЛинейный коэффициент корреляции Коэффициент корреляции отражает
- 25. Коэффициент детерминацииКоэффициент детерминации ( - R-квадрат)
- 26. Коэффициент детерминацииВ частном случае линейной зависимости
- 27. Взаимная информацияВзаимная информация — статистическая функция двух случайных
- 28. Измерение степени связи однотипных объектов Принцип компактности:
- 29. Мера различий: Метрики (расстояния) abd(a,b) = |
- 30. Мера различий: Метрики (расстояния) zxy
- 31. Мера различий: Метрики (расстояния) Примеры различных метрик:
- 32. Мера различий: Метрики (расстояния) Примеры различных метрик:
- 33. Мера различий: Метрики (расстояния) Примеры различных метрик:Композиция метрик:
- 34. Мера различий: Метрики (расстояния) *Обобщения понятия метрики:
- 35. Мера различий: Метрики (расстояния) *Обобщения понятия метрики:
- 36. Мера различий: Метрики (расстояния) *Обобщения понятия метрики:OSrS(θ)θOSrS(θ)θРассмотрим
- 37. Мера различий: Метрики (расстояния) *Обобщения понятия метрики:ABСвойства
- 38. Напоминание: Векторы и Линейные пространства ВекторВекторное
- 39. Мера различий: Метрики (расстояния) Метрики в нормированных линейных пространствах
- 40. Мера различий: Метрики (расстояния) Метрики в нормированных линейных пространствах
- 41. Мера различий: Метрики (расстояния) Метрики в нормированных линейных пространствах
- 42. Мера различий: Метрики (расстояния) Метрики в нормированных линейных пространствахОбобщённая мера расстояний предложенная Германом Минковским:
- 43. Мера различий: Метрики (расстояния) Метрики в нормированных
- 44. Мера различий: Метрики (расстояния) Метрики в нормированных
- 45. Мера различий: Метрики (расстояния) Метрики в нормированных линейных пространствахЕдиничный шар в метриках Минковского:
- 46. Мера различий: Метрики (расстояния) Метрики в нормированных
- 47. Мера различий: Метрики (расстояния) Метрики в нормированных
- 48. Мера различий: Метрики (расстояния) Метрики в нормированных
- 49. Мера различий: Метрики (расстояния) Метрики, не определяемые
- 50. Мера различий: Метрики (расстояния) Метрики, не определяемые
- 51. Мера различий: Метрики (расстояния) Метрики, не определяемые
- 52. Меры сходства Коэффициент сходства — безразмерный показатель,
- 53. Теоретико-множественные меры сходства Наиболее простым коэффициентом сходства
- 54. Меры сходства на основе скалярного произведенияСкалярное произведение —
- 55. Меры сходства на основе скалярного произведения Неравенство Коши — Буняковского
- 56. Нормированная линейная корреляция A • B =
- 57. Нормированная линейная корреляцияНормированный коэффициент линейной корреляции функцийKN(f
- 58. Нормированная линейная корреляцияНормированный коэффициент линейной корреляции функцийKN(f
- 59. Меры сходства и меры различия Нормированный коэффициент
- 60. Меры сходства и меры различия | KN(f,g)
- 61. Информационный поискПоиск информации представляет собой процесс выявления
- 62. Информационный поискПоисковая система — программно-аппаратный комплекс с
- 63. Оценка эффективности поискаНа этом рисунке релевантные точки
- 64. Информационный поиск: индексы и алгоритмы Нечеткий поиск
- 65. Поиск по ключевым словам К группе поиска
- 66. Поиск по ключевым словам Инвертированный файл (ИФ)
- 67. Алгоритмы нечеткого поиска Последовательный поиск предполагает последовательный
- 68. Алгоритмы нечеткого поиска Поиск с использованием хеширования.
- 69. Дерево поиска Двоичное дерево поиска (binary search
- 70. Красно-черное дерево поиска Красно-чёрное дерево — двоичное дерево
- 71. Корреляционное обнаружение и прослеживание объектов на изображениях
- 72. Корреляционное обнаружение и прослеживание объектов на изображениях
- 73. Корреляционное обнаружение объектов на изображениях Эталонный фрагмент
- 74. Корреляционное прослеживание объектов на видеопоследовательностях захваченный эталонрезультат обнаруженияпоследовательность кадров
- 75. Корреляционное прослеживание объектов на видеопоследовательностях захваченный эталонрезультат обнаруженияпоследовательность кадров
- 76. Корреляционное прослеживание объектов на видеопоследовательностях захваченный эталонрезультат обнаружениясмена эталонапоследовательность кадров
- 77. Корреляционное прослеживание объектов на видеопоследовательностях текущий эталонрезультат обнаружениясмена эталонапоследовательность кадров
- 78. Корреляционное прослеживание объектов на видеопоследовательностях текущий эталонрезультат обнаружениясмена эталонапоследовательность кадров
- 79. Корреляционное прослеживание объектов на видеопоследовательностях текущий эталонрезультат обнаружениясмена эталонапоследовательность кадров
- 80. Корреляционное прослеживание объектов на видеопоследовательностях текущий эталонрезультат обнаружениясмена эталонапоследовательность кадров…
- 81. Корреляционное стерео отождествление (stereo matching) Задача стереоотождествления
- 82. Корреляционное стерео отождествление (stereo matching) Геометрические искажения образов
- 83. Корреляционное стерео отождествление (stereo matching) Пример корреляционной функции при отождествлении участков изображений Нормированный коэффициент корреляции
- 84. Корреляционное стерео отождествление (stereo matching) Сопоставление с
- 85. Корреляционное стерео отождествление (stereo matching) Вычисление ЦМР
- 86. Корреляционное стерео отождествление (stereo matching) Пример цифровой
- 87. Стерео отождествление на основе характерных чертТипы используемых
- 88. Стерео отождествление на основе характерных чертПервичное отождествление характерных точек (2/3 ложных пар)
- 89. Стерео отождествление на основе характерных чертПервичное отождествление
- 90. Морфологическая корреляция Пытьеваα = arccos ku, β
- 91. Морфологическая корреляция Пытьеваα = arccos ku, β
- 92. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Содержание лекции
1. Задача сопоставления данных: эквивалентность, инварианты, связь, метрики
и коэффициенты корреляции
2. Информационный поиск: индексы и алгоритмы.
3. Признаковое
описание изображений.4. Корреляционная привязка фрагментов изображений.
5. Корреляционное стерео отождествление.
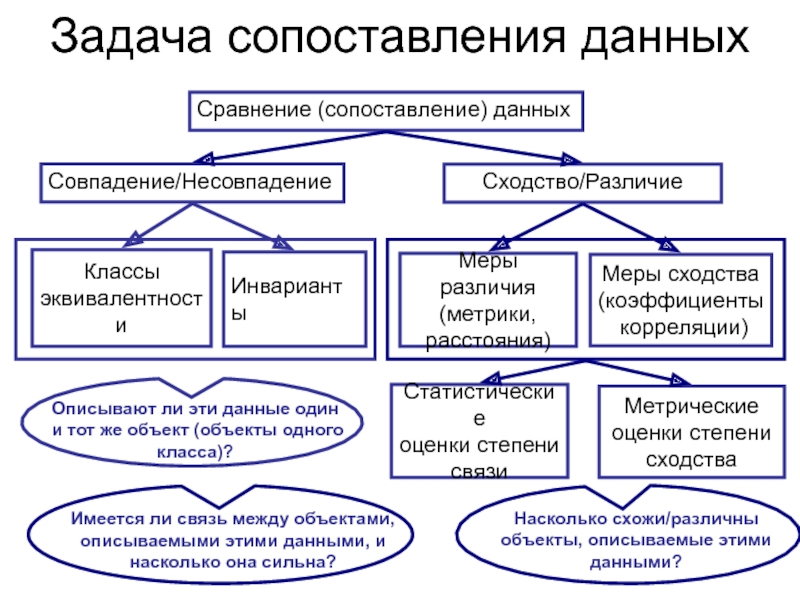
Слайд 3Задача сопоставления данных
Статистические
оценки степени
связи
Метрические
оценки степени
сходства
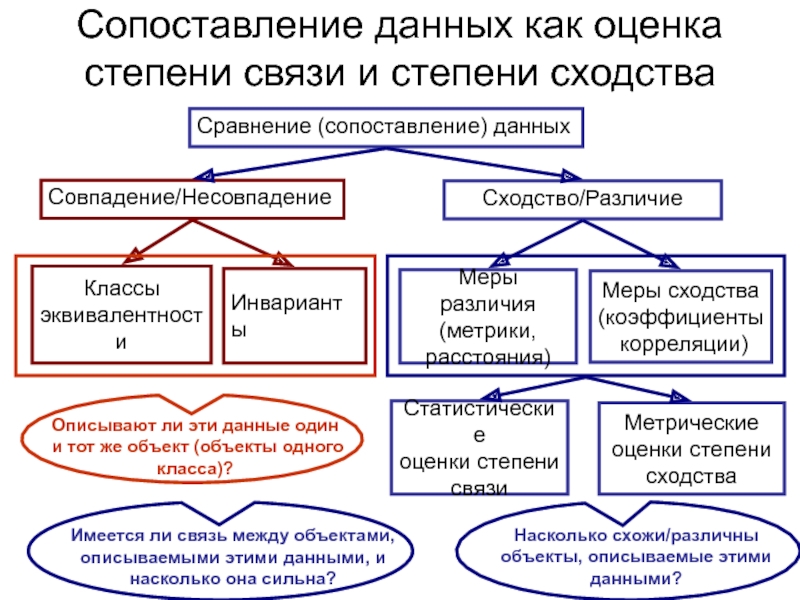
Сравнение (сопоставление) данных
Совпадение/Несовпадение
Сходство/Различие
Классы
эквивалентности
Инварианты
Меры различия
(метрики,
расстояния)
Меры
сходства
(коэффициенты
корреляции)
Описывают ли эти данные один и тот же объект
(объекты одного класса)? Имеется ли связь между объектами, описываемыми этими данными, и насколько она сильна?
Насколько схожи/различны объекты, описываемые этими данными?
Слайд 5Преобразования и эквивалентность
Разбиение множества — это представление его в виде
объединения произвольного количества попарно непересекающихся подмножеств.
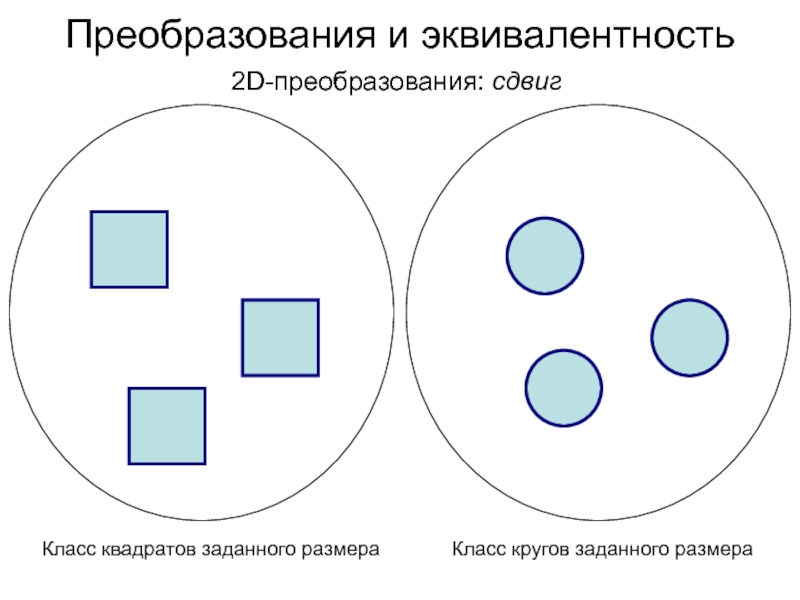
Слайд 6Преобразования и эквивалентность
2D-преобразования: сдвиг
Класс квадратов заданного размера
Класс кругов заданного
размера
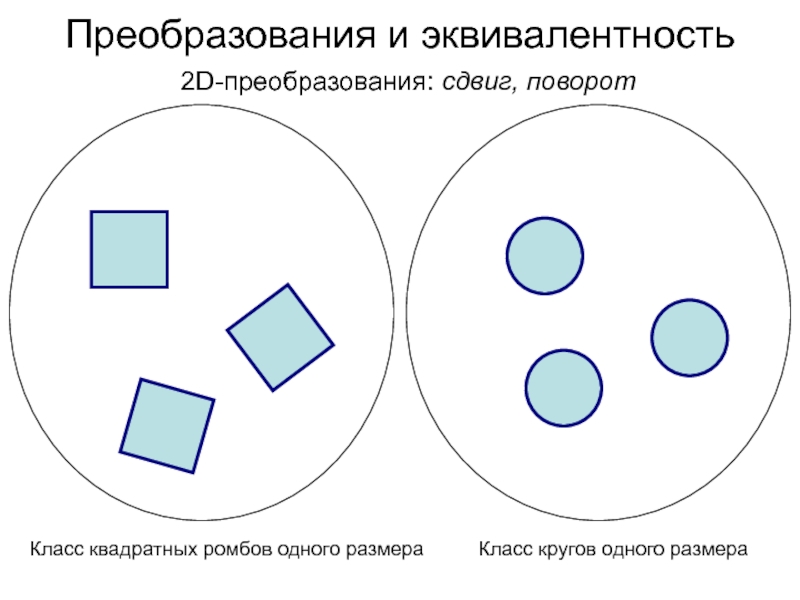
Слайд 7Преобразования и эквивалентность
2D-преобразования: сдвиг, поворот
Класс квадратных ромбов одного размера
Класс
кругов одного размера
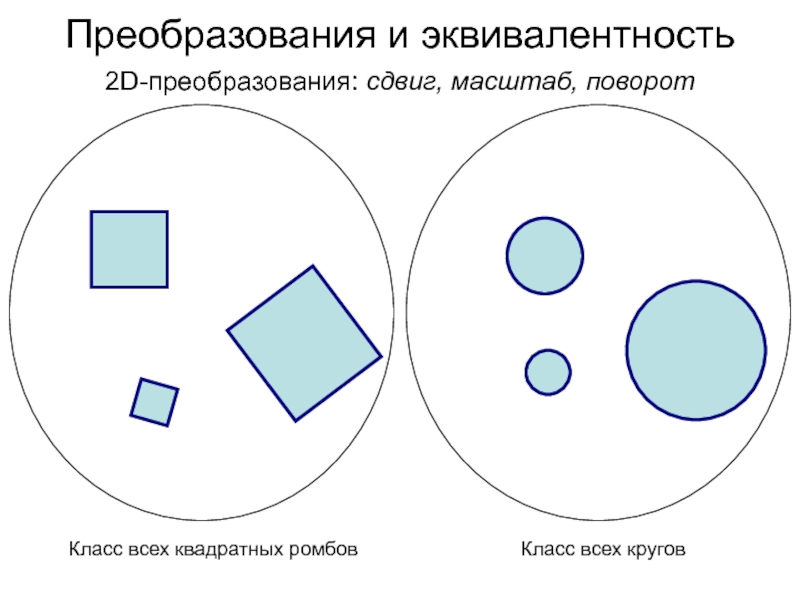
Слайд 8Преобразования и эквивалентность
2D-преобразования: сдвиг, масштаб, поворот
Класс всех квадратных ромбов
Класс
всех кругов
Слайд 9Преобразования и эквивалентность
2D-преобразования: сдвиг, масштаб, поворот
Класс всех квадратных ромбов
Класс
всех кругов
Слайд 10Напоминание: двумерные аффинные преобразования
x' = a11x + a12y
y' = a21x + a22y
Преобразования и эквивалентность
2D-преобразования: аффинные преобразования
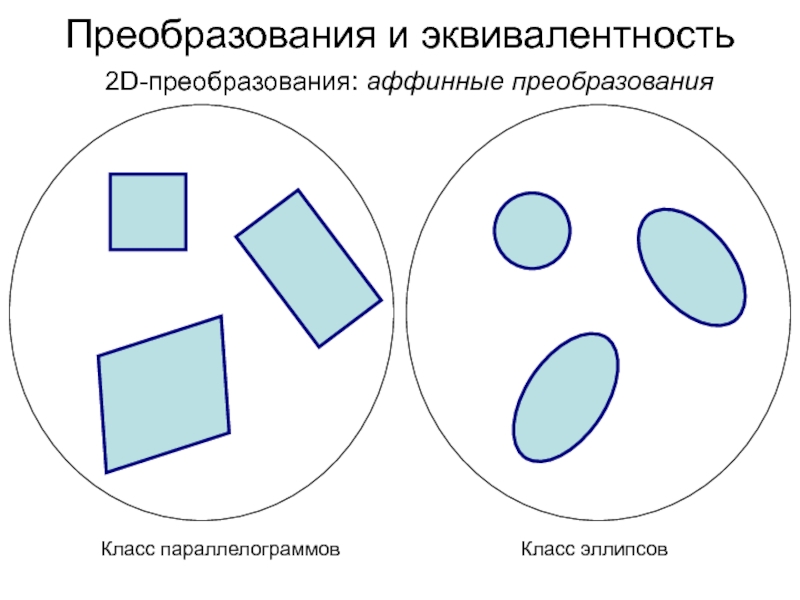
Слайд 11Преобразования и эквивалентность
2D-преобразования: аффинные преобразования
Класс параллелограммов
Класс эллипсов
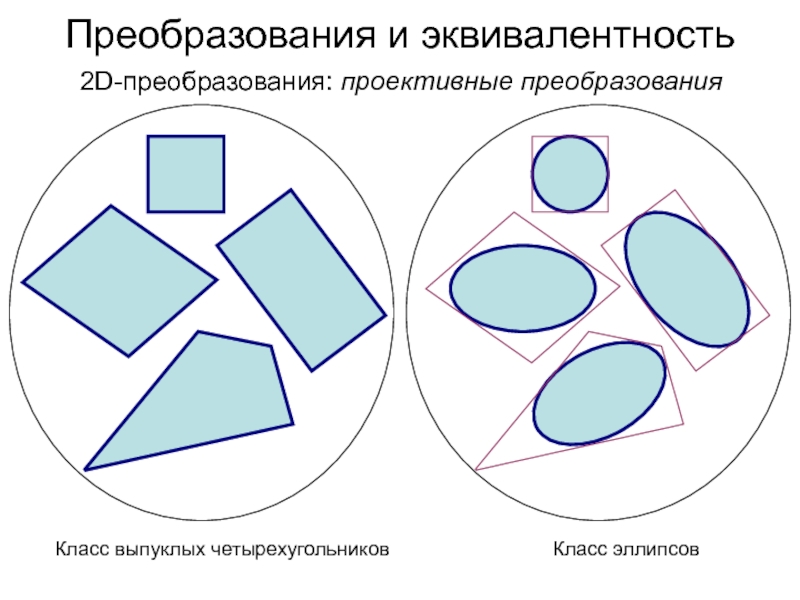
Слайд 12Преобразования и эквивалентность
2D-преобразования: проективные преобразования
Класс выпуклых четырехугольников
Класс эллипсов
Слайд 13Преобразования и инварианты
Инвариант — это свойство некоторого класса (множества)
математических объектов, остающееся неизменным при преобразованиях определённого типа.
Концепция инварианта
является одной из важнейших в математике, поскольку изучение инварианта непосредственно связано с задачами классификации объектов того или иного типа. По существу, целью всякой математической классификации является построение некоторой полной системы инвариантов (по возможности, наиболее простой), то есть такой системы, которая разделяет любые два неэквивалентных объекта из рассматриваемой совокупности. Слайд 14Признаковое описание изображений
Геометрическое описание выделенных областей
Часто используемые признаки:
площадь образа;
положение
центра тяжести образа;
положение центра тяжести образа, рассматриваемого как бинарный;
периметр образа;
отношение
квадрата периметра к площади образа;формат;
компактность;
периметр и площадь описанного прямоугольника минимальной площади;
отношение площади описанного прямоугольника к площади образа;
отношение квадрата периметра описанного прямоугольника к его площади;
формат описанного прямоугольника;
относительные длина и ширина образа.
Слайд 15Признаковое описание изображений
Геометрическое описание выделенных областей
Координаты центра тяжести образа
рассчитываются через статические моменты:
что для бинарной фигуры имеет вид:
а для
полутонового изображения
Слайд 16Признаковое описание изображений
Геометрическое описание выделенных областей
Для вычисления значения признака
F (формата) по контурным точкам образа строится матрица рассеяния
где
и
находятся собственные числа этой матрицыДля определения ориентации находятся собственные векторы матрицы рассеяния:
Чтобы найти величины сторон описанного прямоугольника, ориентированного по собственным векторам, достаточно определить проекции образа на эти векторы.
Слайд 17Признаковое описание изображений
Геометрическое описание выделенных областей
Периметр и площадь минимального
описанного прямоугольника рассчитываются по следующим формулам, где Т1 и Т2
- стороны описанного прямоугольника:Отношение площади описанного прямоугольника к площади образа рассчитывается по формуле:
Отношение квадрата периметра описанного прямоугольника к его площади рассчитывается по формуле:
Формат описанного прямоугольника:
Относительные длина и ширина:
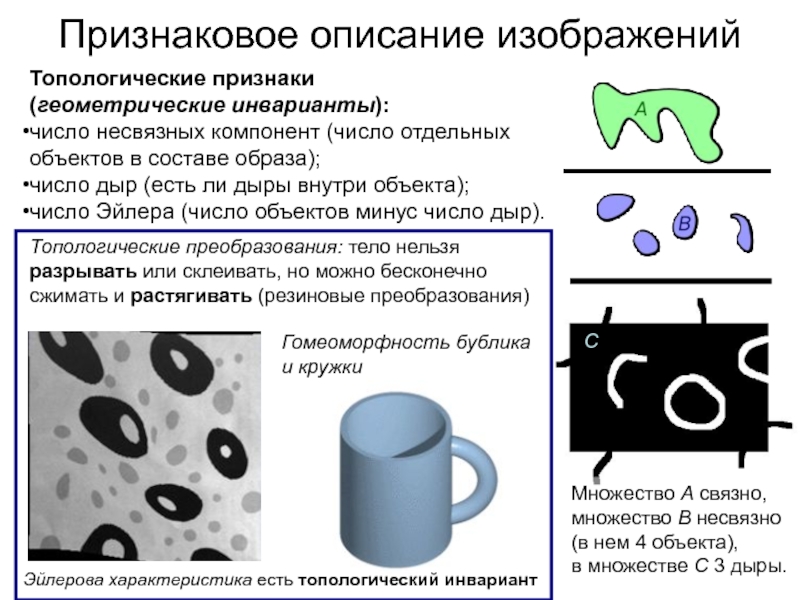
Слайд 18Признаковое описание изображений
Топологические признаки
(геометрические инварианты):
число несвязных компонент (число отдельных
объектов в составе образа);
число дыр (есть ли дыры внутри объекта);
число
Эйлера (число объектов минус число дыр).Множество A связно,
множество B несвязно (в нем 4 объекта),
в множестве C 3 дыры.
Топологические преобразования: тело нельзя разрывать или склеивать, но можно бесконечно сжимать и растягивать (резиновые преобразования)
С
Эйлерова характеристика есть топологический инвариант
Гомеоморфность бублика и кружки
Слайд 19Признаковое описание изображений
Инвариантные моменты
моменты, инвариантные к смещению:
где Ω -
образ в декартовой системе координат (x,y); B(x,y) - значение функции
интенсивности (x,y);xc, yc - координаты центра тяжести образа.
моменты, инвариантные к изменению масштаба:
моменты, инвариантные к повороту:
где
Слайд 20Сопоставление данных как оценка степени связи и степени сходства
Статистические
оценки степени
связи
Метрические
оценки степени
сходства
Сравнение (сопоставление) данных
Совпадение/Несовпадение
Сходство/Различие
Классы
эквивалентности
Инварианты
Меры различия
(метрики,
расстояния)
Меры сходства
(коэффициенты
корреляции)
Описывают ли эти данные
один и тот же объект (объекты одного класса)? Имеется ли связь между объектами, описываемыми этими данными, и насколько она сильна?
Насколько схожи/различны объекты, описываемые этими данными?
Слайд 21Статистическая корреляция
Корреляция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин.
При
этом изменения значений одной или нескольких из этих величин сопутствуют
систематическому изменению значений другой или других величин.Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным.
Положительная корреляция — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной.
Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. При этом переменные могут быть разного типа (разной размерности, разной природы).
Слайд 22Ковариация
Ковариация (или корреляционный момент) является совместным центральным моментом второго порядка.
Ковариация
определяется как математическое ожидание произведения отклонений случайных величин
где M —
математическое ожидание. Свойства ковариации:
Ковариация двух независимых случайных величин X и Y равна нулю.
Абсолютная величина ковариации двух случайных величин X и Y не превышает среднего геометрического их дисперсий:
Ковариация имеет размерность, равную произведению размерности случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа
,
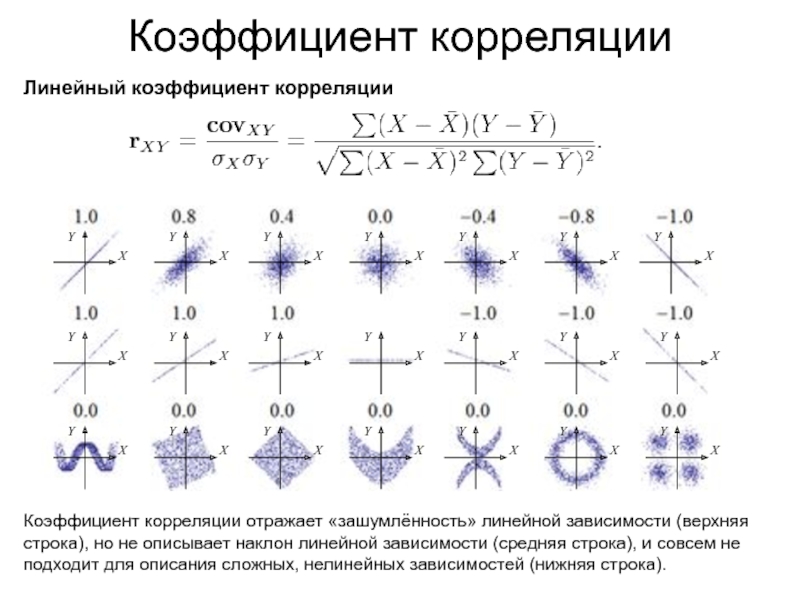
Слайд 24Коэффициент корреляции
Линейный коэффициент корреляции
Коэффициент корреляции отражает «зашумлённость» линейной зависимости
(верхняя строка), но не описывает наклон линейной зависимости (средняя строка),
и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).Слайд 25Коэффициент детерминации
Коэффициент детерминации ( - R-квадрат) — это доля
дисперсии) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью
зависимости (регрессии), то есть объясняющими переменными.Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной.
Его рассматривают как универсальную меру связи одной случайной величины от множества других.
Линейная регрессия:
+ ξ
Слайд 26Коэффициент детерминации
В частном случае линейной зависимости является
квадратом так называемого множественного коэффициента корреляции между зависимой переменной и
объясняющими переменными.В частности, для модели парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции между y и x.
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%
(в этом случае коэффициент множественной корреляции превышает по модулю 70%). Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими (коэффициент корреляции превышает 90%). Значение коэффициента детерминации 1 означает функциональную зависимость между переменными.
Слайд 27Взаимная информация
Взаимная информация — статистическая функция двух случайных величин, описывающая количество
информации, содержащееся в одной случайной величине относительно другой. Взаимная информация
определяется через энтропию — статистическая функция двух случайных величин, описывающая количество информации, содержащееся в одной случайной величине относительно другой. Взаимная информация определяется через энтропию и условную энтропию — статистическая функция двух случайных величин, описывающая количество информации, содержащееся в одной случайной величине относительно другой. Взаимная информация определяется через энтропию и условную энтропию двух случайных величин какСвойства взаимной информации:
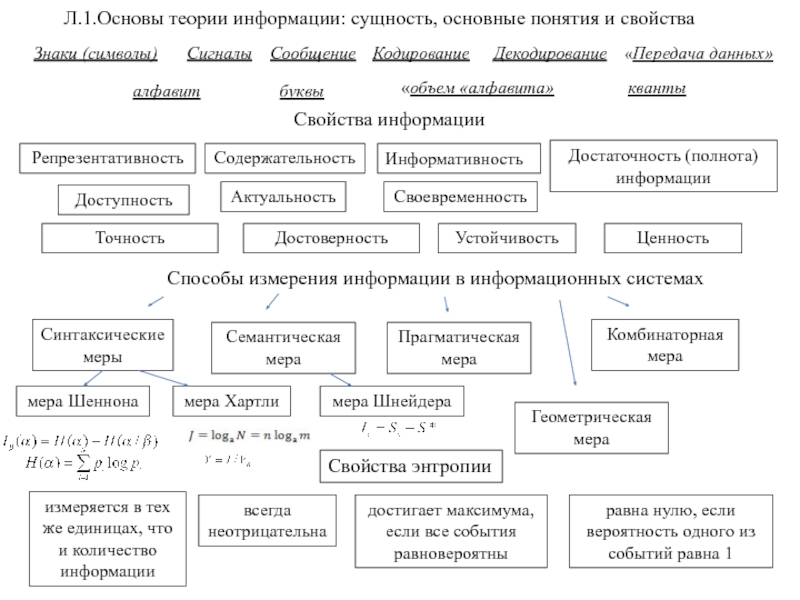
Слайд 28
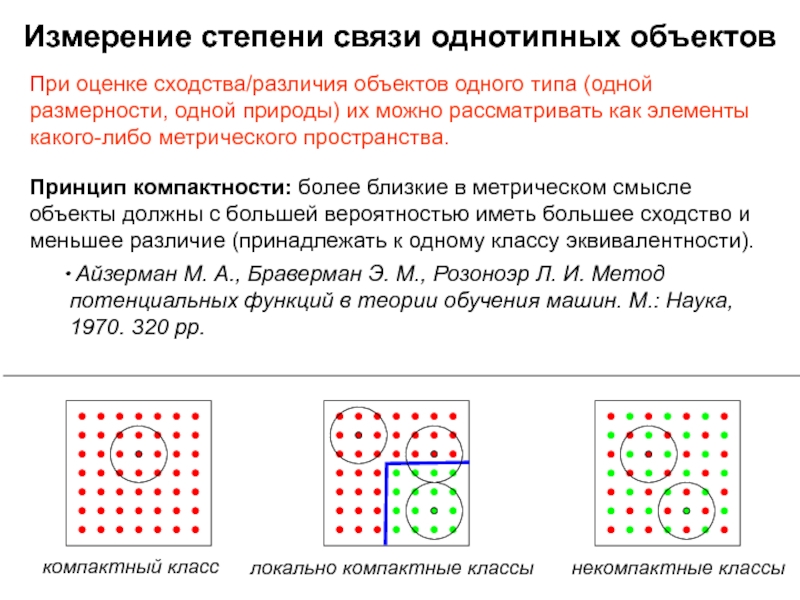
Измерение степени связи однотипных объектов
Принцип компактности: более близкие в
метрическом смысле объекты должны с большей вероятностью иметь большее сходство
и меньшее различие (принадлежать к одному классу эквивалентности).Айзерман М. А., Браверман Э. М., Розоноэр Л. И. Метод потенциальных функций в теории обучения машин. М.: Наука, 1970. 320 pp.
компактный класс
локально компактные классы
некомпактные классы
При оценке сходства/различия объектов одного типа (одной размерности, одной природы) их можно рассматривать как элементы какого-либо метрического пространства.
Слайд 29Мера различий: Метрики (расстояния)
a
b
d(a,b) = | b – a
|
a
b
A
B
d(a,b) = | b – a |
b – a
x
x
y
d(a,b)
= √(xa-xb)2+(ya-yb)2Слайд 36Мера различий: Метрики (расстояния)
*Обобщения понятия метрики:
O
S
rS(θ)
θ
O
S
rS(θ)
θ
Рассмотрим множество точек на
плоскости со следующей квазиметрикой.
Пусть задана некая выпуклая фигура (структурирующий элемент)
S с полюсом O, граница которой ∂S не содержит полюс и описывается в ее собственных полярных координатах непрерывной циклической функцией (переменным радиусом) rS(θ), θ∈[0,2π).Размером фигуры S назовем максимальное значение ее радиуса r(S). Фигуру с центром O и размером r будем обозначать S(O,r).
Эксцентриситетом e(S) фигуры S назовем максимальное отношение rS(θ)/rS(θ-π), θ∈[0,2π).
Определим квазирасстояние dS(A,B) как размер r такой фигуры S(A,r), которая касается точки B: B∈∂S(A,r).
Слайд 37Мера различий: Метрики (расстояния)
*Обобщения понятия метрики:
A
B
Свойства квазирасстояния dS(A,B)
dS(A,B) ≥
0, dS(A,B) = 0 ⇔ A = B
2) dS(A,B) ≤
e(S) dS(B,A), 1 ≤ e(S) < ∞3) dS(A,B) + dS(B,C) ≥ dS(A,C)
dS(A,B)
dS(B,A)
θ
d(A,B) = dS(A,B) rS(θBA) = dS(B,A) rS(θAB)
d(A,B)
A
B
Частный случай – круговая фигурная квазиметрика совпадает с центрально симметричной евклидовой метрикой e(S)=1.
Слайд 38Напоминание:
Векторы и Линейные пространства
Вектор
Векторное пространство
Два вектора
u, v и вектор их суммы
Определение: "Вектор" это такой математический
объект, для которого определены операции сложения векторов и умножения вектора на число.Примечание: Как и "чисел", "векторов" в математике множество. Например, функции также образуют векторное пространство.
Слайд 42Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах
Обобщённая мера
расстояний предложенная Германом Минковским:
Слайд 43Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах
Расстояние Хэмминга —
число позиций, в которых соответствующие символы двух слов одинаковой длины
различны. В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых q-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.Примеры:
"Манхэттенская
метрика" (метрика
городских кварталов)
Х
Y
d(X,Y) = S(X∪Y) - S(X∩Y)
Слайд 44Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах
Евклидово расстояние
между точками p и q это длина отрезка pq.
В
Декартовых координатах, если p = (p1, p2,…, pn) и q = (q1, q2,…, qn)две точки в Евклидовом пространстве, длина отрезка p q равна:
Расстояние Чебышева
Слайд 45Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах
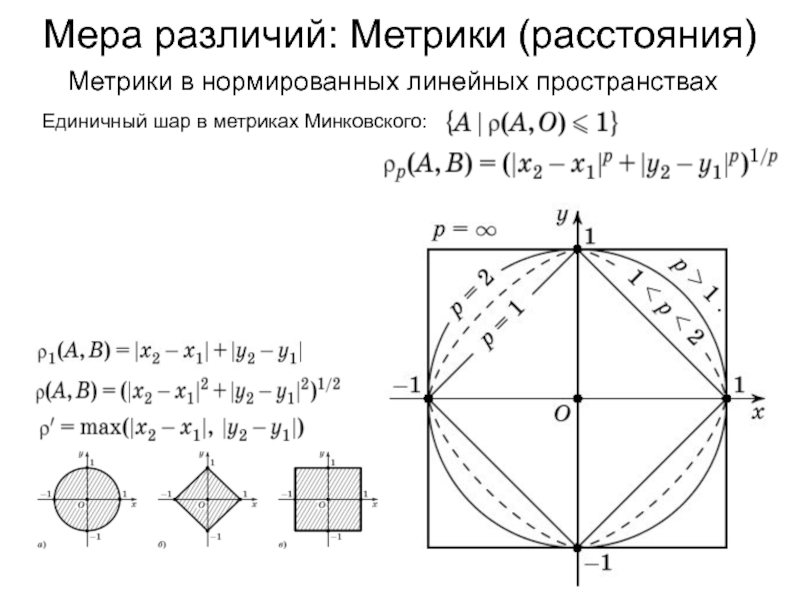
Единичный шар
в метриках Минковского:
Слайд 46Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах
Расстояния между
функциями:
ρ(f1,f2) = ∫x∈[a,b] | f1(x) – f2 (x) | dx
ρ(f1,f2)
= √ ∫x∈[a,b] ( f1(x) – f2 (x) )2 dxметрика L1
метрика L2
метрика L∞
Слайд 47Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах
Метрика Хаусдорфа
есть естественная метрика, определённая на множестве всех непустых компактных подмножеств
метрического пространства.Пример:
Расстояние между кривыми
Слайд 48Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах
Метрика Хаусдорфа
есть естественная метрика, определённая на множестве всех непустых компактных подмножеств
метрического пространства.Х
Y
DH(Х,Y)
Слайд 49Мера различий: Метрики (расстояния)
Метрики, не определяемые нормой
Французская железнодорожная
метрика является необычным примером метрики. Название этой метрики произошло из-за
очень централизованно проложенной (особенно раньше) железнодорожной сети Франции, в которой чуть ли не все пути сходились в Париже. Например, чтобы добраться по железной дороге из Страсбурга в Лион, нужно сделать крюк в 400 км через Париж в связи с тем, что нет прямого сообщения.В невырожденном случае, то есть когда существуют неколлинеарные векторы, французская железнодорожная метрика — простейший пример метрики, которая не порождается нормой.
Слайд 50Мера различий: Метрики (расстояния)
Метрики, не определяемые нормой
Расстояние Левенштейна
(также редакционное расстояние и) между двумя строками в теории информации
и компьютерной лингвистие — это минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на другой, необходимых для превращения одной строки в другую.Впервые задачу упомянул в 1965 году советский математик Владимир Иосифович Левенштейн.
Если к списку разрешённых операций добавить транспозицию (два соседних символа меняются местами), получается расстояние Дамерау — Левенштейна.
Расстояние Левенштейна и его обобщения применяются:
для исправления ошибок в слове (в поисковых системах, базах данных, при вводе текста, при автоматическом распознавании отсканированого текста или речи).
для сравнения текстовых файлов утилитой diff и ей подобными. Здесь роль «символов» играют строки, а роль «строк» — файлы.
в биоинформатике для сравнения генов, хромосом и белков.
Слайд 51Мера различий: Метрики (расстояния)
Метрики, не определяемые нормой
Редакционным предписанием
называется последовательность действий, необходимых для получения из первой строки второй
кратчайшим образом.Обычно действия обозначаются так: D (delete) — удалить, I (insert) — вставить, R (replace) — заменить, M (match) — совпадение.
Например, для 2-х строк «CONNECT» и «CONEHEAD» можно построить следующую таблицу преобразований:
Цены операций могут зависеть от вида операции (вставка, удаление, замена) и/или от участвующих в ней символов, отражая разную вероятность мутаций в биологии, разную вероятность разных ошибок при вводе текста и т. д. В общем случае:
w(a, b) — цена замены символа a на символ b
w(ε, b) — цена вставки символа b
w(a, ε) — цена удаления символа a
Слайд 52Меры сходства
Коэффициент сходства — безразмерный показатель, применяемый для количественного
определения степени сходства объектов (данных).
Большинство коэффициентов нормированы и находятся
в диапазоне от 0 (сходство отстутствует) до 1 (полное сходство).Слайд 53Теоретико-множественные меры сходства
Наиболее простым коэффициентом сходства является мера абсолютного
сходства, которая является числом общих элементов (признаков) двух сравниваемых объектов:
Коэффициент
сходства Жаккара: Меры включения
Это несимметричные меры, которые показывают степень сходства (включения) одного объекта относительно другого:
A
B
или .
меры включения Сёренсена
меры включения Жаккара .
Слайд 54Меры сходства на основе скалярного произведения
Скалярное произведение — операция над двумя
векторами — операция над двумя векторами, результатом которой является число (скаляр),
не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x.Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.
Обычно используется одно из следующих обозначений:
или (обозначениеили (обозначение Дирака, часто применяемое
в квантовой механике для векторов состояния):
.
Обычно предполагается что скалярное
произведение положительно определено, то есть
для всех .
A • B = |A| |B| cos(θ)
Слайд 56Нормированная линейная корреляция
A • B = |A| |B| cos(θ)
KN(A,B)
=
〈A,B〉
|| A || || B ||
|| A || =
; || B || = √〈A,A〉
√〈B,B〉
Нормированный коэффициент линейной корреляции:
Слайд 57Нормированная линейная корреляция
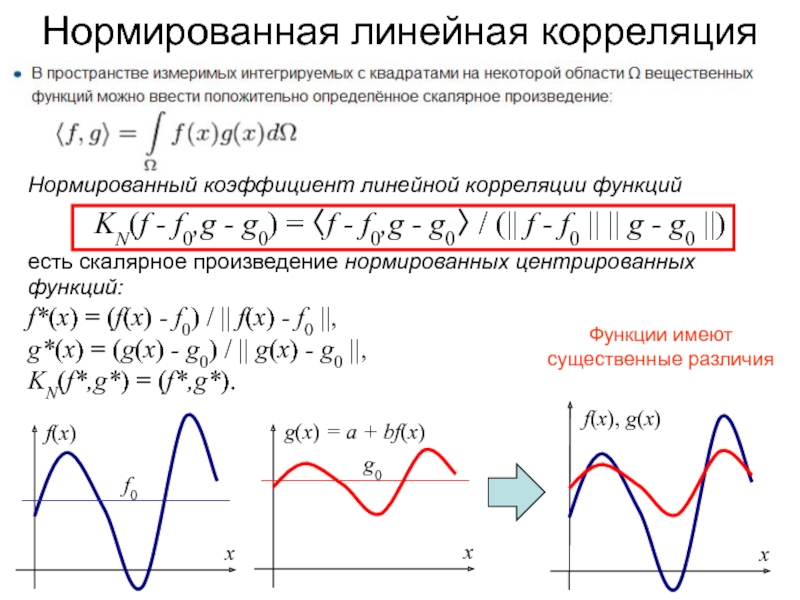
Нормированный коэффициент линейной корреляции функций
KN(f - f0,g -
g0) = 〈f - f0,g - g0〉 / (|| f
- f0 || || g - g0 ||)есть скалярное произведение нормированных центрированных функций:
f*(x) = (f(x) - f0) / || f(x) - f0 ||,
g*(x) = (g(x) - g0) / || g(x) - g0 ||,
KN(f*,g*) = (f*,g*).
f(x)
x
g(x) = a + bf(x)
x
f0
g0
f(x), g(x)
x
Функции имеют
существенные различия
Слайд 58
Нормированная линейная корреляция
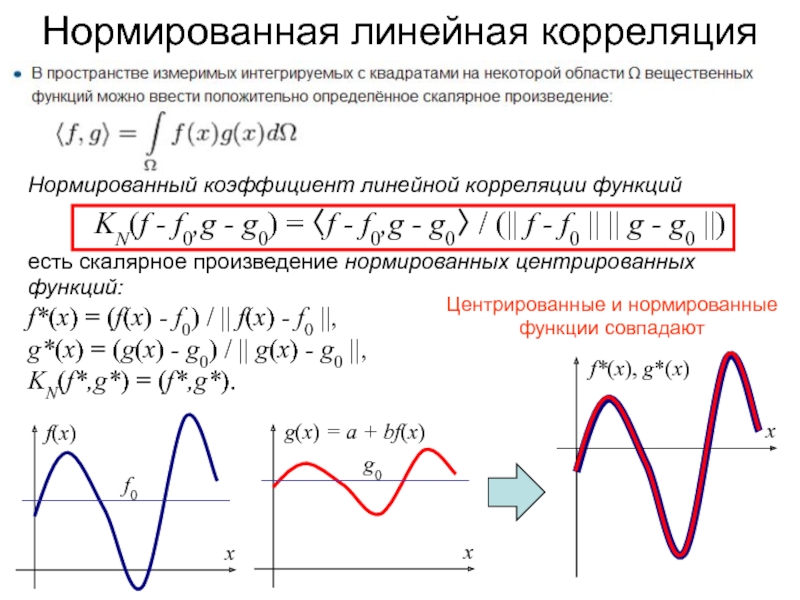
Нормированный коэффициент линейной корреляции функций
KN(f - f0,g -
g0) = 〈f - f0,g - g0〉 / (|| f
- f0 || || g - g0 ||)есть скалярное произведение нормированных центрированных функций:
f*(x) = (f(x) - f0) / || f(x) - f0 ||,
g*(x) = (g(x) - g0) / || g(x) - g0 ||,
KN(f*,g*) = (f*,g*).
f(x)
x
g(x) = a + bf(x)
x
f0
g0
f*(x), g*(x)
x
Центрированные и нормированные
функции совпадают
Слайд 59Меры сходства и меры различия
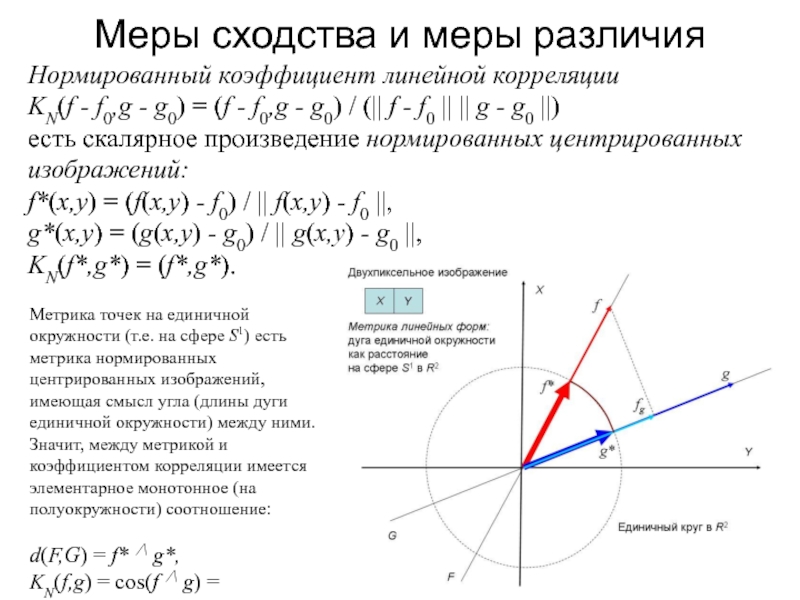
Нормированный коэффициент линейной корреляции
KN(f -
f0,g - g0) = (f - f0,g - g0) /
(|| f - f0 || || g - g0 ||)есть скалярное произведение нормированных центрированных изображений:
f*(x,y) = (f(x,y) - f0) / || f(x,y) - f0 ||,
g*(x,y) = (g(x,y) - g0) / || g(x,y) - g0 ||,
KN(f*,g*) = (f*,g*).
Метрика точек на единичной окружности (т.е. на сфере S1) есть метрика нормированных центрированных изображений, имеющая смысл угла (длины дуги единичной окружности) между ними. Значит, между метрикой и коэффициентом корреляции имеется элементарное монотонное (на полуокружности) соотношение:
d(F,G) = f* ∧ g*,
KN(f,g) = cos(f ∧ g) = cos(d(F,G)).
Слайд 60Меры сходства и меры различия
| KN(f,g) | = |
cos(f ∧ g) | = | cos( d(F,G) ) |,
откуда следует неравенство треугольника для коэффициентов корреляции:| KN(f,g) | ≥ KN(f,w) KN(w,g) – √(1 – K2N(f,w)) √(1 – K2N(w,g)),
поскольку
cos(a + b) = cos(a) cos(b) – sin(a) sin(b),
sin(a) = √(1 – cos2(a)).
Пример. Если
KN(f,w) = KN(w,g) = 1/√2 = 0,707…,
то корреляция двух крайних изображений между собой может оказаться даже нулевой:
| KN(f,g) | ≥ 0.
Это объясняет многие известные примеры «плохого» поведения теоретически «хороших» мер сходства на реальных данных.
Слайд 61Информационный поиск
Поиск информации представляет собой процесс выявления в некотором множестве
документов представляет собой процесс выявления в некотором множестве документов (текстов
представляет собой процесс выявления в некотором множестве документов (текстов) всех тех, которые посвящены указанной теме (предмету), удовлетворяют заранее определенному условию поиска (запросу представляет собой процесс выявления в некотором множестве документов (текстов) всех тех, которые посвящены указанной теме (предмету), удовлетворяют заранее определенному условию поиска (запросу) или содержат необходимые (соответствующие информационной потребности) факты представляет собой процесс выявления в некотором множестве документов (текстов) всех тех, которые посвящены указанной теме (предмету), удовлетворяют заранее определенному условию поиска (запросу) или содержат необходимые (соответствующие информационной потребности) факты, сведения, данные.Рассматривается поиск информации в документах, поиск самих документов, извлечение метаданных из документов, поиск текста, изображений, видео и звука в локальных реляционных базах данных, в гипертекстовых базах данных таких, как Интернет и локальные интранет-системы.
Запрос — это формализованный способ выражения информационных потребностей пользователем системы. Для выражения информационной потребности используется язык поисковых запросов — это формализованный способ выражения информационных потребностей пользователем системы. Для выражения информационной потребности используется язык поисковых запросов, синтаксис — это формализованный способ выражения информационных потребностей пользователем системы. Для выражения информационной потребности используется язык поисковых запросов, синтаксис варьируется от системы к системе. Кроме специального языка запросов — это формализованный способ выражения информационных потребностей пользователем системы. Для выражения информационной потребности используется язык поисковых запросов, синтаксис варьируется от системы к системе. Кроме специального языка запросов, современные поисковые системы — это формализованный способ выражения информационных потребностей пользователем системы. Для выражения информационной потребности используется язык поисковых запросов, синтаксис варьируется от системы к системе. Кроме специального языка запросов, современные поисковые системы позволяют вводить запрос на естественном языке.
Объект запроса — это информационная сущность, которая хранится в базе информационно-поисковой системы (ИПС). Процесс занесения объектов поиска в ИПС называется индексацией. ИПС не всегда хранит точную копию объекта, нередко вместо неё хранится суррогат или индекс.
Слайд 62Информационный поиск
Поисковая система — программно-аппаратный комплекс с веб-интерфейсом, предоставляющий возможность
поиска информации в Интернете.
Под поисковой системой обычно подразумевается сайтПод поисковой
системой обычно подразумевается сайт, на котором размещён интерфейс (фронт-энд) системы.Поисковая машина (поисковый движок) — комплекс программ, предназначенный для поиска информации. Обычно является частью поисковой системы.
Основными критериями качества работы поисковой машины являются релевантность работы поисковой машины являются релевантность (степень соответствия запроса и найденного, т.е. уместность результата), полнота базы работы поисковой машины являются релевантность (степень соответствия запроса и найденного, т.е. уместность результата), полнота базы, учёт морфологии работы поисковой машины являются релевантность (степень соответствия запроса и найденного, т.е. уместность результата), полнота базы, учёт морфологии языка.
Индексация - извлечение из документов информации, важной для поиска, преобразование этой информации в формат, удобный для поисковой машины и сохранение этой информации в базу данных поисковой машины.
Поиск по базе данных проиндексированных документов включает:
Нахождение документов, соответствующих поисковому запросу
Ранжирование документов в соответствии с их релевантностью поисковым запросам
Кластеризацию (группировку) документов
Слайд 63Оценка эффективности поиска
На этом рисунке релевантные точки (rel) находятся слева
от прямой, а точки, найденные поисковой системой (retr), находятся в
овале. Области красного цвета представляют ошибки поисковой системы. Красная область слева - это релевантные точки, не найденные системой (пропуск событияНа этом рисунке релевантные точки (rel) находятся слева от прямой, а точки, найденные поисковой системой (retr), находятся в овале. Области красного цвета представляют ошибки поисковой системы. Красная область слева - это релевантные точки, не найденные системой (пропуск события), красная область справа - найденные, но нерелевантные точки (ложная тревога).Точность - это пропорция левой зелёной области по отношению к овалу (горизонтальная стрелка).
Полнота - это пропорция левой зелёной области к области слева от прямой (диагональная стрелка).
Определяется как отношение числа найденных релевантных документов к общему числу найденных документов
Отношение числа найденных релевантных документов, к общему числу релевантных документов в базе
Слайд 64Информационный поиск:
индексы и алгоритмы
Нечеткий поиск – поиск по ключевым
словам с учётом возможных произвольных ошибок в написании ключевого слова
и/или целевого запроса.Поисковые индексы – структуры данных, используемые при поиске:
векторные и кластерные модели;
модели на основе ключевых слов.
Инвертированные файлы
Сигнатурные файлы
Поисковые метрики - меры сходства или различия между словами:
Расстояния Хемминга, Левенштейна, Дамерау-Левенштейна, Джаро, Джаро-Уинклера и др.
Методы поиска
Последовательный поиск (полный перебор всех слов словаря);
Метод расширения выборки (query extension);
Метод n-грамм;
Поиск с использованием хеширования;
Методы, основанные на неравенстве треугольника (триангуляционные деревья).
Слайд 65Поиск по ключевым словам
К группе поиска по ключевым словам
относится большинство современных технологий поиска, используемых в информационно-поисковых системах, в
том числе – системах поиска в сети Интернет, обрабатывающих запросы на естественных языках (Google, Yandex…).В процессе поиска такие системы производят выборку всех документов, содержащих хотя бы одно ключевое слово (грамматическую форму данного слова или его синоним), а затем ранжируют результаты поиска по степени соответствия (релевантности) документов поисковому запросу.
В основе поиска по ключевым словам лежит использование специализированных индексных словарей двух основных типов: инвертированные файлы и сигнатурные файлы.
Слайд 66Поиск по ключевым словам
Инвертированный файл (ИФ) является аналогом предметного
указателя в конце книги. ИФ – множество пар
адрес вхождения ключевого слова в документ>. Детализация адреса слова может быть различной: на уровне документа, абзаца, непосредственного места слова в тексте. Основным недостатком ИФ является его большой объём. Если не применять специальные методы сжатия списков вхождений, то размер ИФ может превышать размер исходного текстового массива в 2-3 раза.Сигнатурные файлы (СФ) содержат сигнатуры данных, представляющие собой их упрощенные профили, в которых каждый элемент кодируется одним битом (есть вхождение ключевого фрагмента или нет такого вхождения). Размер СФ составляет порядка 50% от исходных данных. Основным недостатком сигнатурных файлов является то, что множество сигнатур однозначно определяет множество документов, но не каждый документ конкретно. Поэтому после предварительной выборки данных по сигнатурам необходима их дополнительная обработка с целью уточненной проверки на соответствие запросу.
В настоящее время разработаны методы построения сжатых ИФ, вследствие чего область применения СФ несколько сузилась. Сжатые ИФ существенно превосходят СФ по производительности для коротких запросов, но проигрывают им на длинных и очень длинных запросах. В среднем короткие запросы встречаются гораздо чаще, поэтому в большинстве систем на сегодняшний день преимущество отдается ИФ.
Слайд 67Алгоритмы нечеткого поиска
Последовательный поиск предполагает последовательный перебор слов из
словаря и сравнение каждого из них с запросом в соответствии
с принятой метрикой. Основным достоинством последовательного поиска являются простота реализации и достаточно высокая скорость работы, связанная с тем, что при последовательном считывании данных с диска компьютера в виде больших файлов достигается пиковая скорость чтения. Время поиска в данном случае пропорционально размеру словаря. Кроме того, этот метод позволяет без ограничений реализовать многофункциональный поиск, например, по подстроке или по регулярным выражениям.Метод расширения выборки. Суть данного метода заключается в построении множества всевозможных «ошибочных» слов, например, получающихся из исходного в результате одной операции редактирования Левенштейна, после чего построенные поисковые запросы ищутся в словаре на точное совпадение.
Метод n-грамм. Идея метода заключается в построении инвертированного файла, в котором роль документов играют слова, а роль слов – подстроки длины n, называемые n-граммами. Основной недостаток метода – большой размер вспомогательного индексного файла (в 10-20 раз больше размера исходного словаря).
Слайд 68Алгоритмы нечеткого поиска
Поиск с использованием хеширования. Идея, лежащая в
основе методов хеширования, состоит в подборе отображения (хеш-функции) слова, например,
во множество чисел или строк, сохраняющего основные характеристики исходного слова и устойчивого к наиболее распространённым ошибкам. Такая функция позволяет разбить слова словаря на группы и производить последовательный поиск внутри группы, вычисляемой по поисковому шаблону. Например, для разбиения на группы иногда используют хеширование по некоторому количеству первых символов слова (метод trie-деревьев). Другим известным примером является хеш-функция Soundex, встроенная в коммерческие СУБД Sybase, MS SQL Server, Oracle.Триангуляционные деревья позволяют индексировать множества произвольной структуры, при условии, что на них задана метрика. В основу построения триангуляционных деревьев положена идея расположения близких в смысле заданной метрики объектов в одинаковых поддеревьях. Метод эффективен в ситуации, когда операция сравнения достаточно дорогостоящая (например, при поиске в базах изображений или больших документов), и позволяет существенно сократить количество сравнений.
Слайд 69Дерево поиска
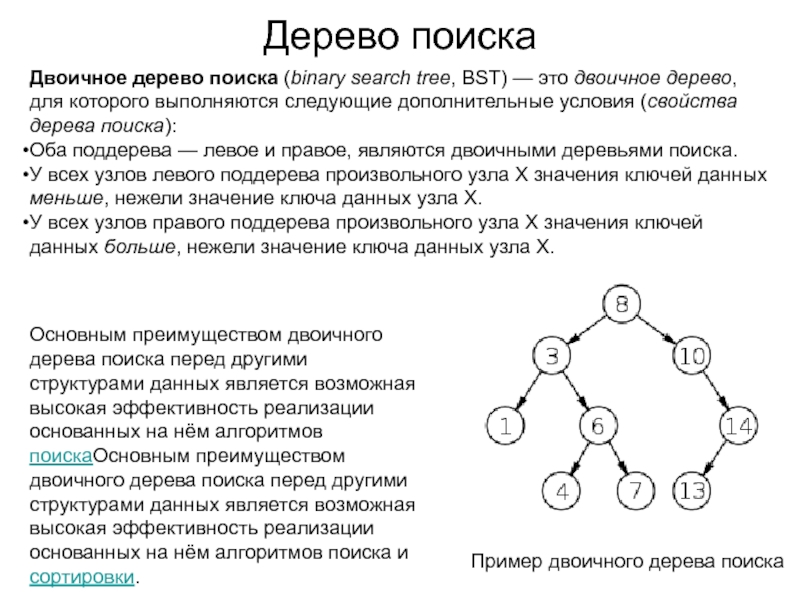
Двоичное дерево поиска (binary search tree, BST) —
это двоичное дерево, для которого выполняются следующие дополнительные условия (свойства
дерева поиска):Оба поддерева — левое и правое, являются двоичными деревьями поиска.
У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных узла X.
У всех узлов правого поддерева произвольного узла X значения ключей данных больше, нежели значение ключа данных узла X.
Пример двоичного дерева поиска
Основным преимуществом двоичного дерева поиска перед другими структурами данных является возможная высокая эффективность реализации основанных на нём алгоритмов поискаОсновным преимуществом двоичного дерева поиска перед другими структурами данных является возможная высокая эффективность реализации основанных на нём алгоритмов поиска и сортировки.
Слайд 70Красно-черное дерево поиска
Красно-чёрное дерево — двоичное дерево поиска, в котором
каждый узел имеет атрибут цвет, принимающий значения красный или черный.
К
красно-чёрным деревьям дополнительно применяются следующие требования:Узел либо красный, либо чёрный.
Корень — чёрный.
Все листья — черные.
Оба потомка каждого красного узла — черные.
Всякий простой путь от данного узла до любого листового узла, являющегося его потомком, содержит одинаковое число черных узлов.
Эти ограничения реализуют критическое свойство красно-черных деревьев: путь от корня до самого дальнего листа не более чем в два раза длиннее пути от корня до ближайшего листа. Так как операции вставки, удаления и поиска значений требуют в худшем случае времени, пропорционального длине дерева, эта верхняя граница высоты позволяет красно-чёрным деревьям быть более эффективными в худшем случае, чем обычные двоичные деревья поиска.
Пример красно-чёрного дерева
Слайд 71Корреляционное обнаружение
и прослеживание объектов на изображениях
Согласованная фильтрация бинарных изображений
Если изображение рассматривается не как полутоновое, а как бинарное, то
в этом случае эталонное обнаружение объектов сводится к процедуре согласованной фильтрации. Часто сравниваются контурные изображения.Согласованная фильтрация представляет собой разновидность оконной фильтрации. При этом создается окно, совпадающее по форме с искомым объектом, назначается центральный пиксел окна (reference point), после чего производится проход окном по входному изображению. В каждом возможном положении окна подсчитывается число ненулевых элементов окна. Если это число больше некоторого порога (ранга), то принимается решение об обнаружении объекта в этой точке, и в центральный пиксел текущего окна на выходном изображении (предварительно обнуленном) выставляется значение 1.
Иногда при этом еще проверяется то условие, что в "окаймлении" согласованного окна число единиц не превышает некоторого порога ("согласованная фильтрация с окаймлением").
Слайд 72Корреляционное обнаружение
и прослеживание объектов на изображениях
Расстояние между изображениями
Как правило,
для вычисления расстояний между изображениями используется следующая формула:
где f(x,y), g(x,y)
- функции интенсивности, X – апертура зоны поиска; величина α∈[1,∞] - определяет характеристики используемой метрики.
Нормированный коэффициент корреляции
со свойствами.
1) -1 ≤ k(f,g) ≤1;
2) k(f,g) = 1 ⇔ g = af + b; a>0, b;
3) k(f,g) = -1 ⇔ g = af + b; a<0, b.
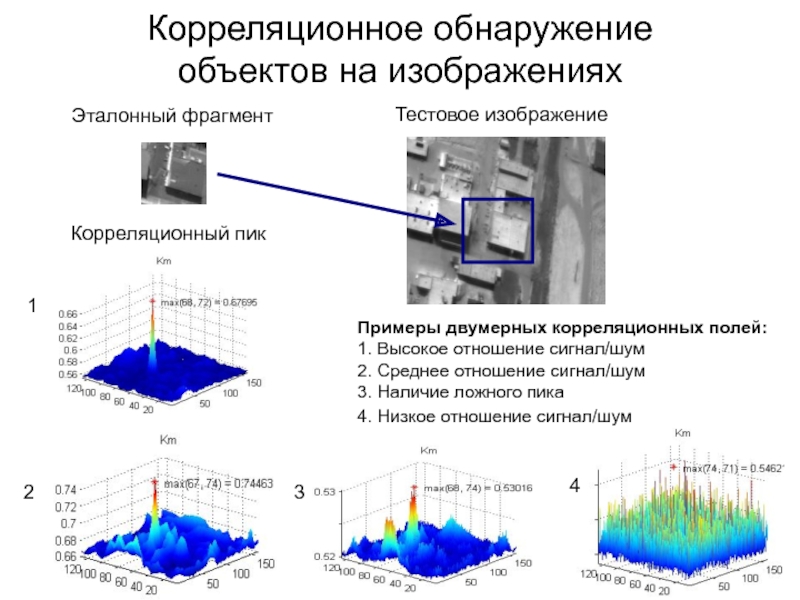
Слайд 73Корреляционное обнаружение
объектов на изображениях
Эталонный фрагмент
Тестовое изображение
Корреляционный пик
Примеры двумерных корреляционных полей:
1. Высокое отношение сигнал/шум
2. Среднее отношение сигнал/шум
3.
Наличие ложного пика4. Низкое отношение сигнал/шум
1
2
3
4
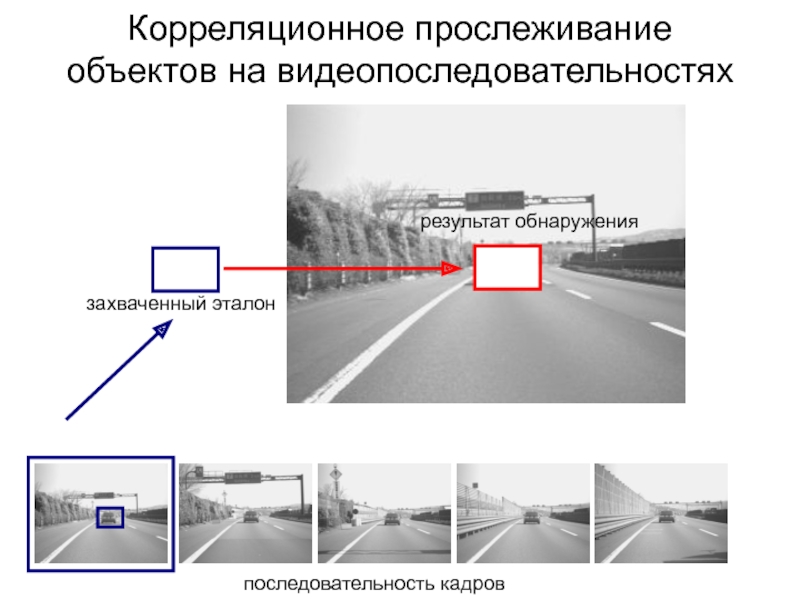
Слайд 74Корреляционное прослеживание
объектов на видеопоследовательностях
захваченный эталон
результат обнаружения
последовательность кадров
Слайд 75Корреляционное прослеживание
объектов на видеопоследовательностях
захваченный эталон
результат обнаружения
последовательность кадров
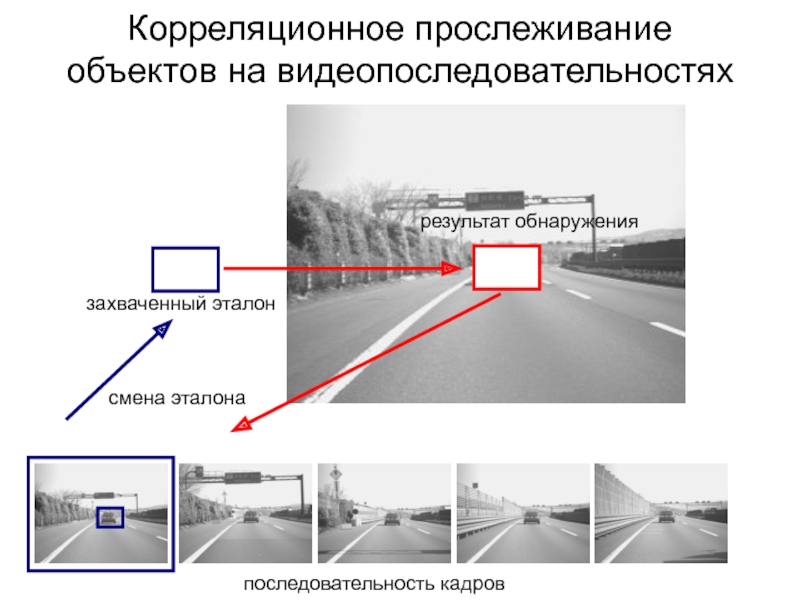
Слайд 76Корреляционное прослеживание
объектов на видеопоследовательностях
захваченный эталон
результат обнаружения
смена эталона
последовательность кадров
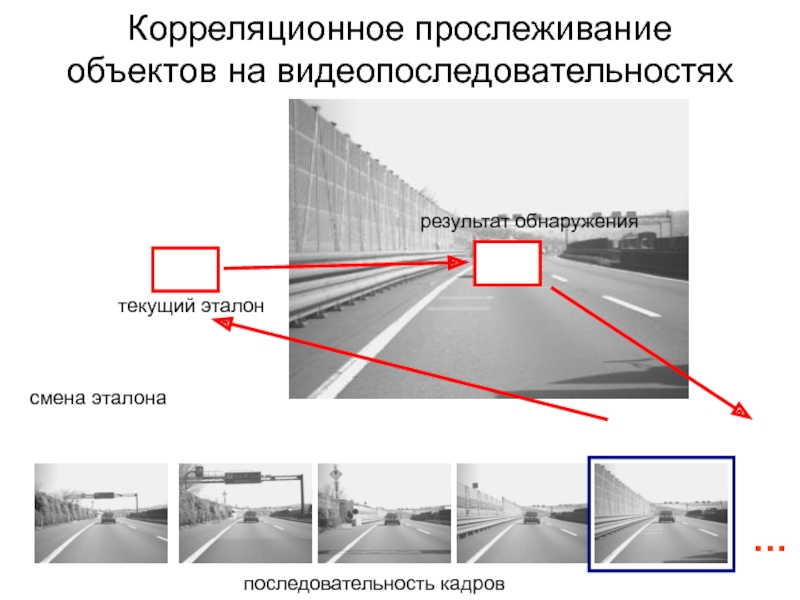
Слайд 77Корреляционное прослеживание
объектов на видеопоследовательностях
текущий эталон
результат обнаружения
смена эталона
последовательность кадров
Слайд 78Корреляционное прослеживание
объектов на видеопоследовательностях
текущий эталон
результат обнаружения
смена эталона
последовательность кадров
Слайд 79Корреляционное прослеживание
объектов на видеопоследовательностях
текущий эталон
результат обнаружения
смена эталона
последовательность кадров
Слайд 80Корреляционное прослеживание
объектов на видеопоследовательностях
текущий эталон
результат обнаружения
смена эталона
последовательность кадров
…
Слайд 81Корреляционное стерео
отождествление (stereo matching)
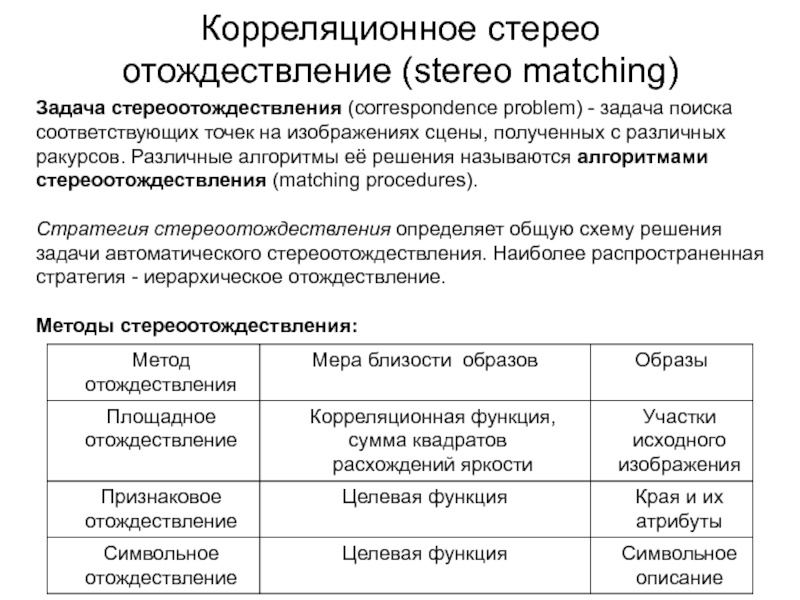
Задача стереоотождествления (correspondence problem) - задача
поиска соответствующих точек на изображениях сцены, полученных с различных ракурсов.
Различные алгоритмы её решения называются алгоритмами стереоотождествления (matching procedures).Стратегия стереоотождествления определяет общую схему решения задачи автоматического стереоотождествления. Наиболее распространенная стратегия - иерархическое отождествление.
Методы стереоотождествления:
Слайд 83Корреляционное стерео
отождествление (stereo matching)
Пример корреляционной функции при отождествлении участков
изображений
Нормированный коэффициент корреляции
Слайд 84Корреляционное стерео
отождествление (stereo matching)
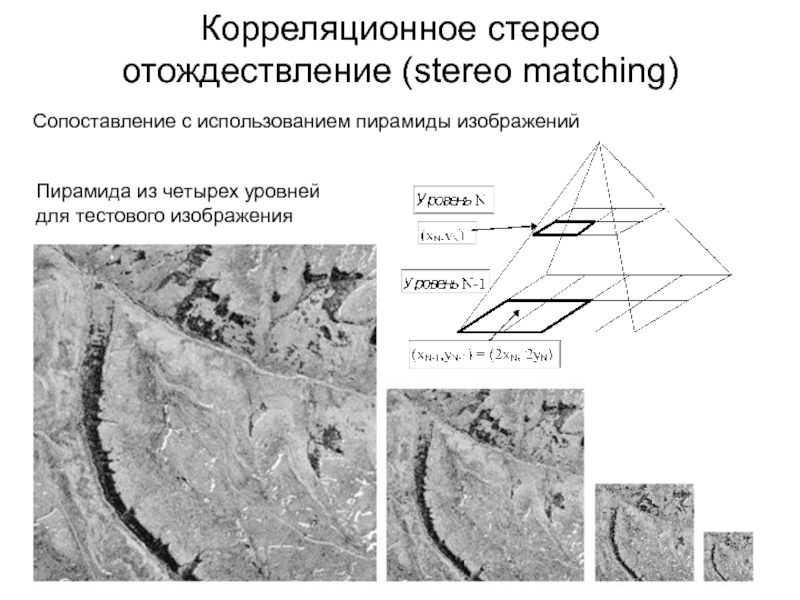
Сопоставление с использованием пирамиды изображений
Пирамида
из четырех уровней для тестового изображения
Слайд 85Корреляционное стерео
отождествление (stereo matching)
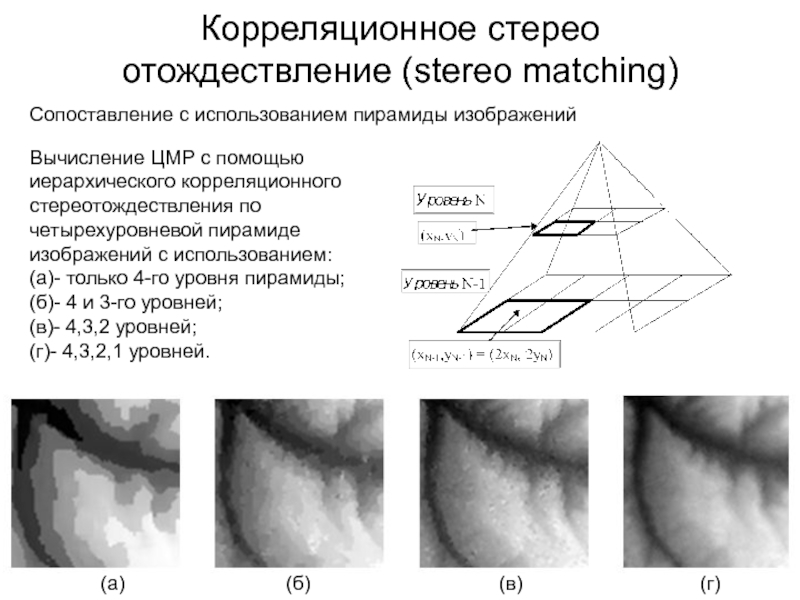
Вычисление ЦМР с помощью иерархического корреляционного
стереотождествления по четырехуровневой пирамиде изображений с использованием:
(а)- только 4-го уровня
пирамиды;(б)- 4 и 3-го уровней;
(в)- 4,3,2 уровней;
(г)- 4,3,2,1 уровней.
Сопоставление с использованием пирамиды изображений
(а) (б) (в) (г)
Слайд 86Корреляционное стерео
отождествление (stereo matching)
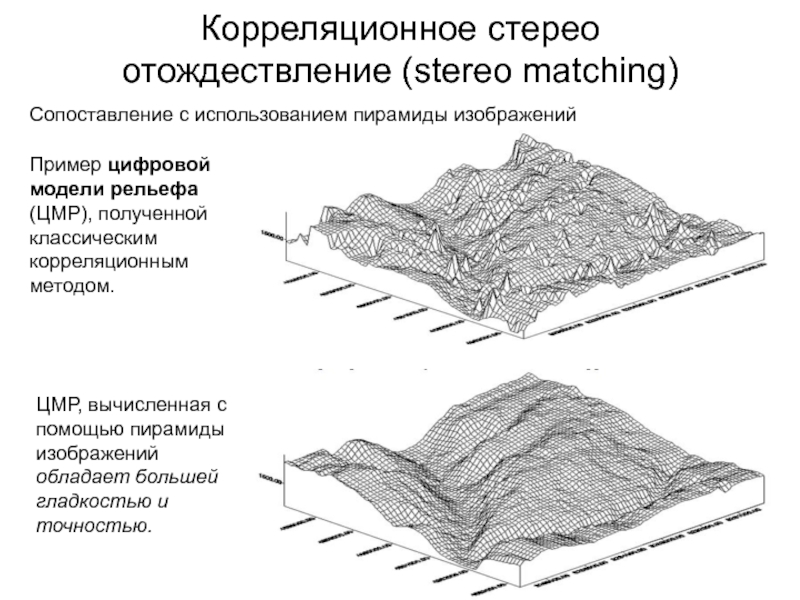
Пример цифровой модели рельефа (ЦМР), полученной
классическим корреляционным методом.
Сопоставление с использованием пирамиды изображений
ЦМР, вычисленная с
помощью пирамиды изображений обладает большей гладкостью и точностью. Слайд 87Стерео отождествление
на основе характерных черт
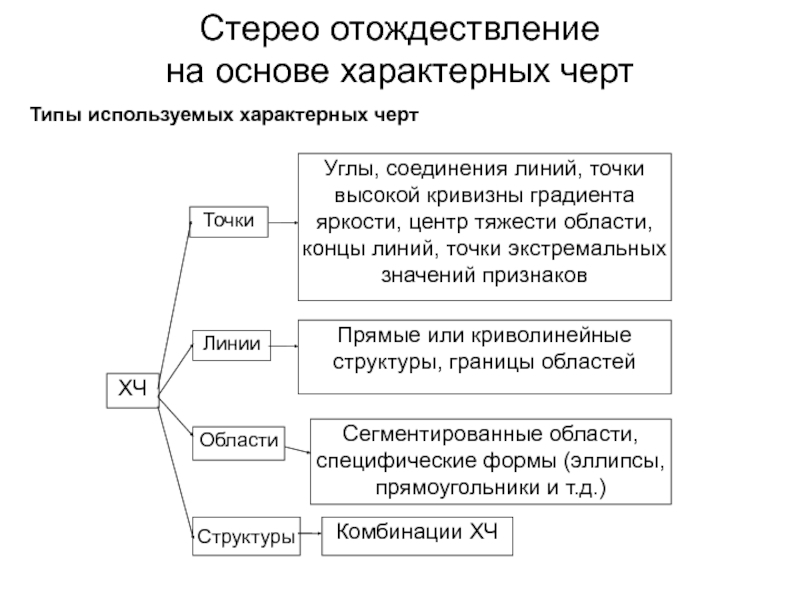
Типы используемых характерных черт
ХЧ
Точки
Углы, соединения линий,
точки высокой кривизны градиента яркости, центр тяжести области, концы линий,
точки экстремальных значений признаковЛинии
Прямые или криволинейные структуры, границы областей
Области
Сегментированные области, специфические формы (эллипсы, прямоугольники и т.д.)
Структуры
Комбинации ХЧ
Слайд 88Стерео отождествление
на основе характерных черт
Первичное отождествление характерных точек (2/3 ложных
пар)
Слайд 89Стерео отождествление
на основе характерных черт
Первичное отождествление характерных точек (2/3 ложных
пар)
Геометрическая фильтрация пар точек (большинство ложных пар удалены)
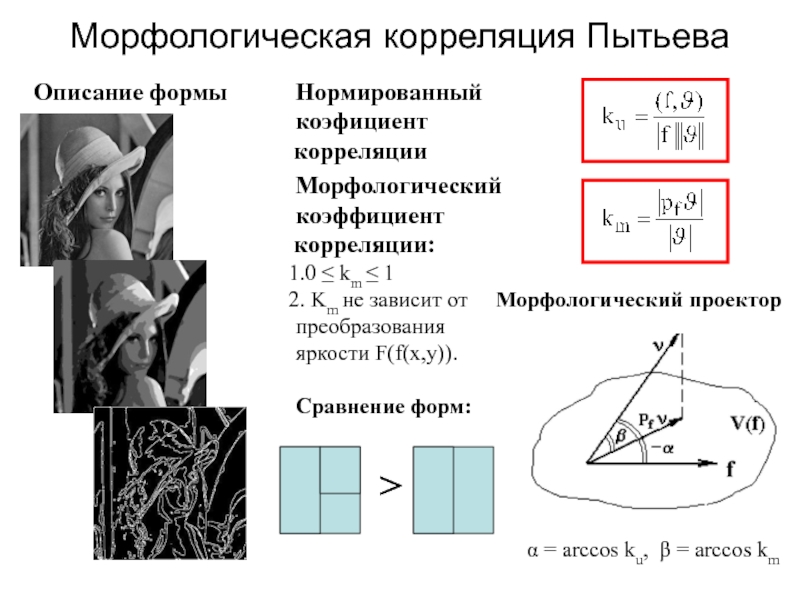
Слайд 90Морфологическая корреляция Пытьева
α = arccos ku, β = arccos km
Нормированный
коэфициент
корреляции
Морфологический
коэффициент
корреляции:
0
≤ km ≤ 1
Km не зависит от
Морфологический проектор
преобразования
яркости F(f(x,y)).Сравнение форм:
Описание формы
>
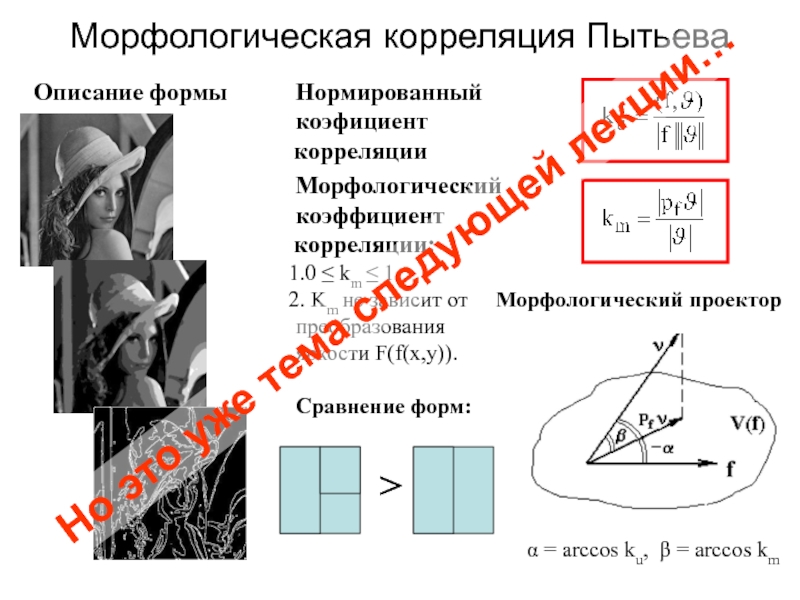
Слайд 91Морфологическая корреляция Пытьева
α = arccos ku, β = arccos km
Нормированный
коэфициент
корреляции
Морфологический
коэффициент
корреляции:
0
≤ km ≤ 1
Km не зависит от
Морфологический проектор
преобразования
яркости F(f(x,y)).Сравнение форм:
Описание формы
>
Но это уже тема следующей лекции…


































![Сравнение и корреляция Мера различий: Метрики (расстояния) Метрики в нормированных линейных пространствахРасстояния между функциями:ρ(f1,f2) Мера различий: Метрики (расстояния) Метрики в нормированных линейных пространствахРасстояния между функциями:ρ(f1,f2) = ∫x∈[a,b] | f1(x) – f2](/img/thumbs/d489b172ec3c658ea815ed427e8242a7-800x.jpg)