Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Старинные системы записи чисел
Содержание
- 1. Старинные системы записи чисел
- 2. Так говорили пифагорейцы, подчёркивая необычайно важную роль чисел в практической деятельности.
- 3. Люди всегда считали и записывали
- 4. Что есть число?Число – это некоторая величина
- 5. Числа
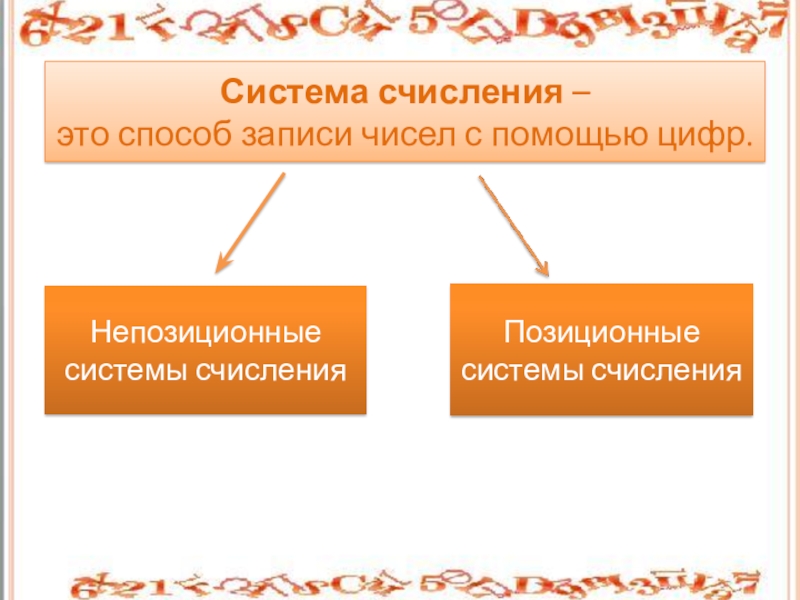
- 6. Позиционные системы счисленияСистема счисления – это способ записи чисел с помощью цифр.Непозиционные системы счисления
- 7. Непозиционные системы счисления - количественные значения символов,
- 8. Единичная непозиционная система счисления
- 9. Древнеегипетская десятичная непозиционная система счисления
- 10. Алфавитная непозиционная система счисления Древней Греции
- 11. Алфавитная система была
- 12. Римская непозиционная система счисления
- 13. Иероглифические и алфавитные системы
- 14. Индийская мультипликативная система счисления;Вавилонская система счисления;Десятичная система
- 15. Вавилонская система счисления Идея
- 16. Десятичная система счисления
- 17. Простота выполнения арифметических операций;Ограниченное количество символов, необходимых
- 18. ЛитератураИнформатика: Учебник для 6 класса / Л.Л.
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Так говорили пифагорейцы,
подчёркивая необычайно важную роль чисел в практической
деятельности.
Слайд 3 Люди всегда считали и записывали числа, даже пять
тысяч лет назад. Но записывали они их по другому ,
по другим правилам. Но в любом случае число изображалось с помощью любого или нескольких символов, которые назывались цифрами.3
2
1
5
7
0
4
6
8
9
I
X
V
C
L
D
M
B
ф
Г
Д
е
s
z
Слайд 5 Числа складываются из цифр
по особым правилам. На разных этапах развития человечества, у разных
народов эти правила были различны и сегодня мы их называем системами счисления.1
8
3
6
9
D
C
L
I
X
I
M
I
X
I
M
Л
Д
Слайд 6Позиционные системы счисления
Система счисления –
это способ записи чисел с
помощью цифр.
Непозиционные системы счисления
Слайд 7Непозиционные системы счисления - количественные значения символов, используемых для записи чисел,
не зависят от их места расположения (позиции) в коде числа.
Единичная
система счисления;Древнеегипетская десятичная непозиционная система счисления;
Римская система счисления;
Греческая алфавитная система счисления;
Славянская алфавитная система счисления.
Возникли раньше позиционных систем счисления.
Слайд 8Единичная
непозиционная система счисления
10 - 11
тысяч лет до н.э., когда у людей появилась потребность в
записи чисел, количество предметов, например, мешков, изображалось нанесением черточек или засечек на какой-либо твёрдой поверхности: камне, глине, дереве. Каждому мешку в такой записи соответствовала одна чёрточка.Учёные называли этот способ записи чисел единичной или унарной системой счисления.
Слайд 9Древнеегипетская десятичная
непозиционная система счисления
Древнеегипетская десятичная непозиционная
система счисления возникла во второй половине третьего тысячелетия до н.
э. Бумаги ещё не было и её заменяла глиняная дощечка, поэтому цифры имели такое начертание. В этой системе счисления использовали в качестве цифр ключевые числа.единица (шест) сотня (свёрнутый пальмовый лист)
десяток (дуга) тысяча (цветок лотоса)
Число 2342 «рисовалось так»
Именно из комбинации таких «цифр» записывались числа и каждая «цифра» повторялась не более 9 раз. Так как десятую цифру можно заменить одним числом, на разряд выше.
I
I
I
Слайд 10Алфавитная непозиционная система
счисления Древней Греции
Наряду
с иероглифическими знаками в древности широко применялись алфавитные системы счисления,
в которых числа изображались буквами алфавита. Так, в Древней Греции числа 1, 2, 3, 4, 5, 6, 7, 8, 9 обозначали первыми девятью буквами греческого алфавита. Для обозначения десятков применялись следующие 9 букв. Для обозначения сотен использовались последние девять букв в алфавите.(Пропуск некоторых записей означает, что в древности алфавит содержал ещё несколько букв)
Слайд 11 Алфавитная система была принята и в
древней Руси. До конца XVII века (до реформы Петра I)
в ней в качестве «цифр» использовали 27 букв кириллицы. Чтобы отличить буквы от цифр над буквами ставился специальный знак - «титло». При этом числовые значения букв возрастали в том же порядке, в каком следовали буквы в греческом алфавите (порядок букв славянского алфавита был немного иным).Обозначения чисел больше 999:
а=1000;
=10000 («тем»);
=100000 («легион»);
=1000000 («леорд»);
=10000000 («ворон»);
=100000000 («колода»)
Славянская алфавитная
непозиционная система счисления
а
Слайд 12Римская
непозиционная система счисления
Римские числа являются примером
полупозиционной системы образования числа, которая сохранилась до наших дней. Применялась
более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки: для числа I (один палец), V (раскрытая ладонь), X (две сложенные ладони. Для обозначения чисел 100, 500 и 1000 стали применять первые буквы, соответствующих латинских слов. Centum – 100, Demi mille -половина тысячи, Mille – тысяча.Римскими цифрами пользовались долго. Ещё 200 лет назад в деловых бумагах должны были обозначаться римскими числами (считалось, что арабские цифры можно подделать).
2012
1000+1000+10+2
MMXII
Слайд 13 Иероглифические и алфавитные системы счисления имели один
существенный недостаток – в них было очень трудно выполнять арифметические
операции. И поэтому в ходе развития человеческого общества эти системы уступили место позиционным системам счисления. Этого неудобства нет у позиционных систем счисления.Недостатки
непозиционных системы счисления
MCMLXXXVI-CDXLIV=?
=?
ЧТОГ+ХПН=?
I
I-
I
Слайд 14Индийская мультипликативная система счисления;
Вавилонская система счисления;
Десятичная система счисления.
Старинные позиционные системы
счисления - количественные значения символов, используемых для записи чисел, зависят от
их места расположения (позиции) в коде числа.Системы счисления, основанные на позиционном
принципе, возникли независимо одна от другой.
Слайд 15Вавилонская система счисления
Идея приписывать цифрам разные
величины в зависимости от того, какую позицию они занимают в
записи числа, впервые появилась в Древнем Вавилоне примерно в III тысячелетии до н.э. Для записи чисел вавилоняне использовали всего два знака: клин вертикальный – единицы и клин горизонтальный - десятки.До нашего времени дошли многие глиняные таблички Древнего Вавилона, на которых решены сложнейшие задачи, такие как вычисление корней, отыскание объёма пирамиды и др.
Слайд 16Десятичная система счисления
Современная десятичная система
счисления возникла приблизительно в V веке н. э. в Индии.
Индийцы познакомились с греческой нумерацией, в которой греки уже использовали для обозначения нулевого разряда символ «0» (первая буква греческого слова Ouden – ничто). Затем они познакомились и с вавилонской системой счисления и соединили её с принципами нумерации греческих чисел. Это был завершающий шаг в создании нашей десятичной системы счисления.Такое изображение десятичных цифр не случайно:
каждая цифра обозначает число, соответствующее углов в ней.
В современной десятичной системе счисления используется 10 арабских цифр. Почему мы называем наши цифры арабскими? С возникшей в Индии десятичной системой счисления первыми познакомились арабы. Они по достоинству её оценили и начали использовать при расчётах в торговых операциях. Именно арабы завезли эту систему счисления в Европу.
Слайд 17Простота выполнения арифметических операций;
Ограниченное количество символов, необходимых для записи чисел;
Удобна
для механического представления чисел.
Достоинства
позиционной системы счисления
Слайд 18Литература
Информатика: Учебник для 6 класса / Л.Л. Босова.- 3-е изд.,
испр. И доп.- М.:БИНОМ. Лаболатория знаний, 2005.
Соколова О.Л. Универсальные поурочные
разработки по информатике. 10 класс. М.:ВАКО, 2006.Картинки в слайдах взяты из коллекции А.Ф. Мещерякова ТОИПКРО.
http://www.google.ru/search?q=%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B+%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F+%D0%B2+%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B0%D1%85&hl=ru&newwindow=1&tbo=u&tbm=isch&source=univ&sa=X&ei=Cvq6UIivEpSP4gS0yoGoAg&ved=0CCsQsAQ&biw=1024&bih=653#hl=ru&newwindow=1&tbo=d&tbm=isch&sa=1&q=%D0%9D%D0%BE%D1%81%D0%B8%D1%82%D0%B5%D0%BB%D1%8F+%D0%B4%D0%BB%D1%8F+%D0%B7%D0%B0%D0%BF%D0%B8%D1%81%D0%B8+%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BB+%D0%B2+%D0%B4%D1%80%D0%B5%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D0%B8&oq=%D0%9D%D0%BE%D1%81%D0%B8%D1%82%D0%B5%D0%BB%D1%8F+%D0%B4%D0%BB%D1%8F+%D0%B7%D0%B0%D0%BF%D0%B8%D1%81%D0%B8+%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BB+%D0%B2+%D0%B4%D1%80%D0%B5%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D0%B8&gs_l=img.3...187263.204330.0.204728.48.39.0.0.0.1.904.3716.2-1j2j0j3j1.7.0...0.0...1c.1.ePRL_-BDhqU&pbx=1&bav=on.2,or.r_gc.r_pw.r_qf.&fp=23766644dd6b420b&bpcl=39314241&biw=1024&bih=610
http://numeration.ru/oct.html
http://www.klgtu.ru/students/literature/inf_asu/1740.html
http://www.google.ru/search?q=%D0%A4%D0%BE%D1%82%D0%BE+12+%D0%BA%D0%B0%D1%80%D0%B0%D0%BD%D0%B4%D0%B0%D1%88%D0%B5%D0%B9+%D0%B2+%D0%BA%D0%BE%D1%80%D0%BE%D0%B1%D0%BA%D0%B5&hl=ru&newwindow=1&tbo=u&tbm=isch&source=univ&sa=X&ei=iA67ULPbOqSL4gTJwYH4AQ&ved=0CCsQsAQ&biw=1024&bih=610
http://www.google.ru/search?q=%D0%A4%D0%BE%D1%82%D0%BE+12+%D0%BA%D0%B0%D1%80%D0%B0%D0%BD%D0%B4%D0%B0%D1%88%D0%B5%D0%B9+%D0%B2+%D0%BA%D0%BE%D1%80%D0%BE%D0%B1%D0%BA%D0%B5&hl=ru&newwindow=1&tbo=u&tbm=isch&source=univ&sa=X&ei=iA67ULPbOqSL4gTJwYH4AQ&ved=0CCsQsAQ&biw=1024&bih=610#hl=ru&newwindow=1&tbo=d&tbm=isch&sa=1&q=%D0%A4%D0%BE%D1%82%D0%BE+%D1%81%D0%B5%D1%80%D0%B2%D0%B8%D0%B7+%D1%87%D0%B0%D0%B9%D0%BD%D1%8B%D0%B9+12+%D0%BF%D0%B5%D1%80%D1%81%D0%BE%D0%BD&oq=%D0%A4%D0%BE%D1%82%D0%BE+%D1%81%D0%B5%D1%80%D0%B2%D0%B8%D0%B7+%D1%87%D0%B0%D0%B9%D0%BD%D1%8B%D0%B9+12+%D0%BF%D0%B5%D1%80%D1%81%D0%BE%D0%BD&gs_l=img.3...156925.166394.2.167092.20.20.0.0.0.8.321.5041.0j2j15j3.20.0...0.0...1c.1.dmcqoGsTs8A&pbx=1&bav=on.2,or.r_gc.r_pw.r_qf.&fp=23766644dd6b420b&bpcl=39314241&biw=1024&bih=610
http://www.google.ru/search?q=%D0%A4%D0%BE%D1%82%D0%BE+12+%D0%BA%D0%B0%D1%80%D0%B0%D0%BD%D0%B4%D0%B0%D1%88%D0%B5%D0%B9+%D0%B2+%D0%BA%D0%BE%D1%80%D0%BE%D0%B1%D0%BA%D0%B5&hl=ru&newwindow=1&tbo=u&tbm=isch&source=univ&sa=X&ei=iA67ULPbOqSL4gTJwYH4AQ&ved=0CCsQsAQ&biw=1024&bih=610#hl=ru&newwindow=1&tbo=d&tbm=isch&sa=1&q=%D0%A4%D0%BE%D1%82%D0%BE+%D0%BB%D0%BE%D0%B6%D0%BA%D0%B8+12+%D0%BF%D0%B5%D1%80%D1%81%D0%BE%D0%BD&oq=%D0%A4%D0%BE%D1%82%D0%BE+%D0%BB%D0%BE%D0%B6%D0%BA%D0%B8+12+%D0%BF%D0%B5%D1%80%D1%81%D0%BE%D0%BD&gs_l=img.3...194968.198298.4.199390.7.6.1.0.0.1.629.1708.0j1j4j5-1.6.0...0.0...1c.1.Mn1PbZQWVa4&pbx=1&bav=on.2,or.r_gc.r_pw.r_qf.&fp=23766644dd6b420b&bpcl=39314241&biw=1024&bih=610