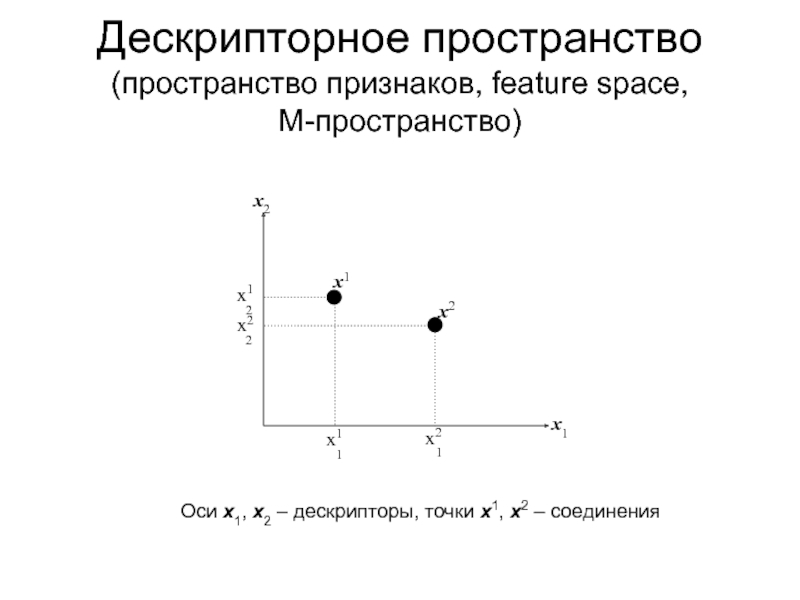
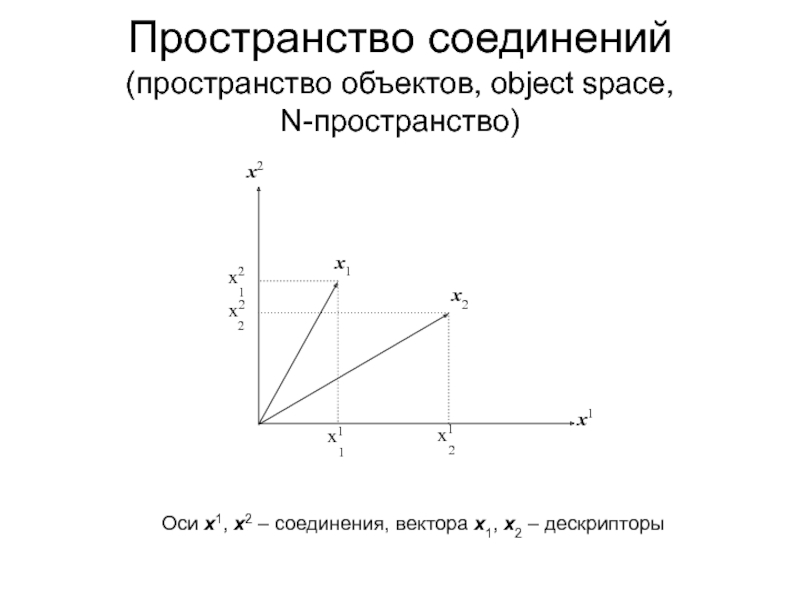
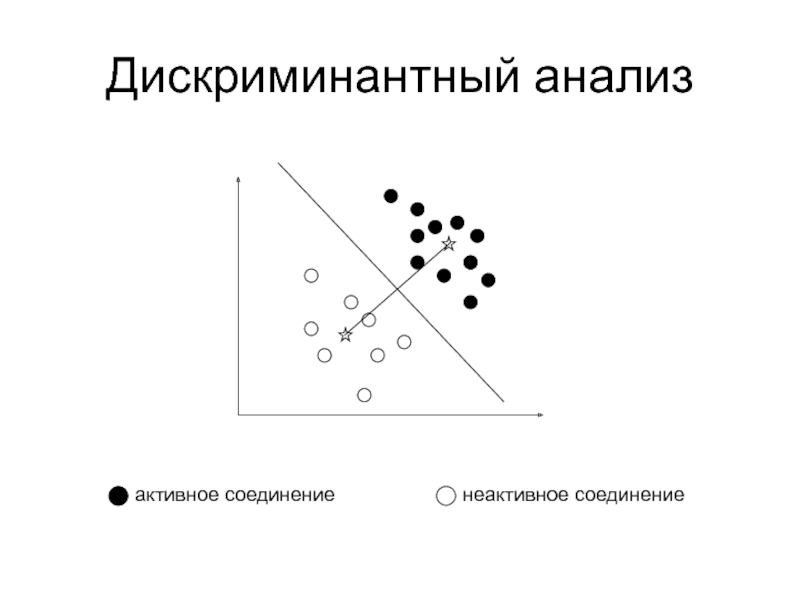
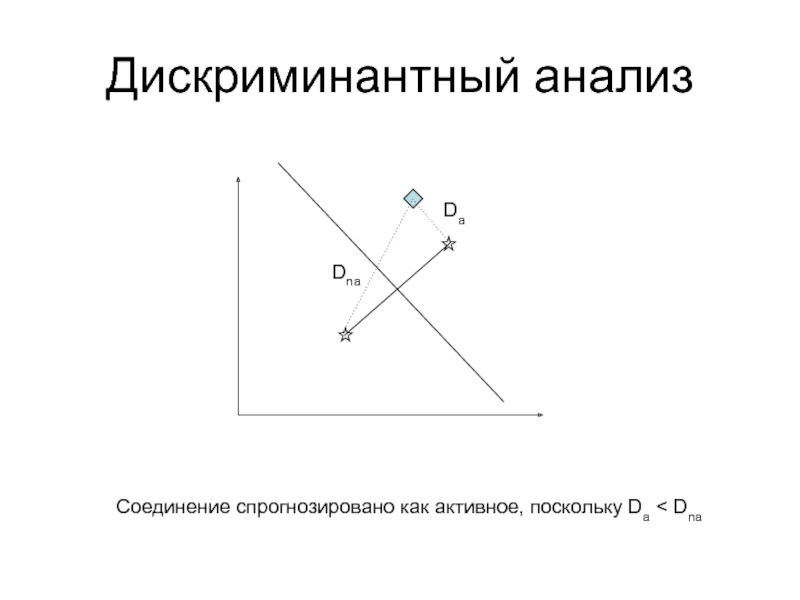
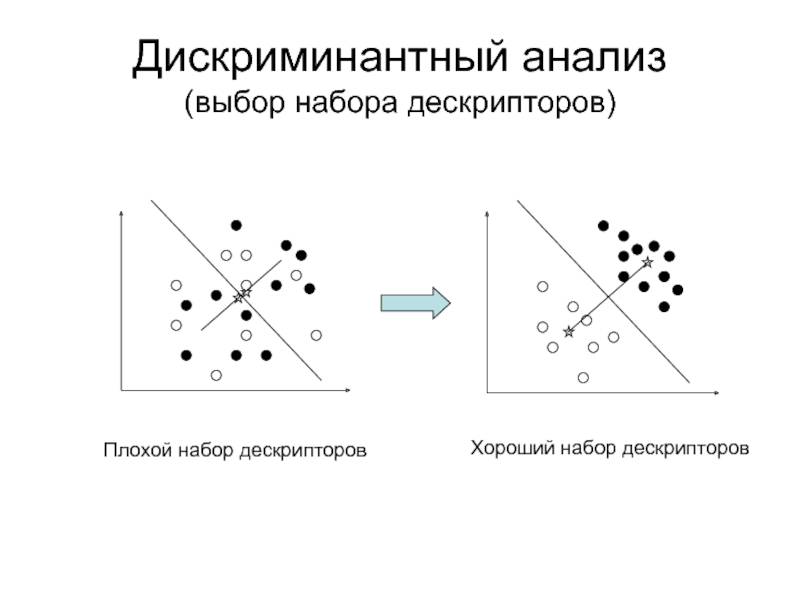
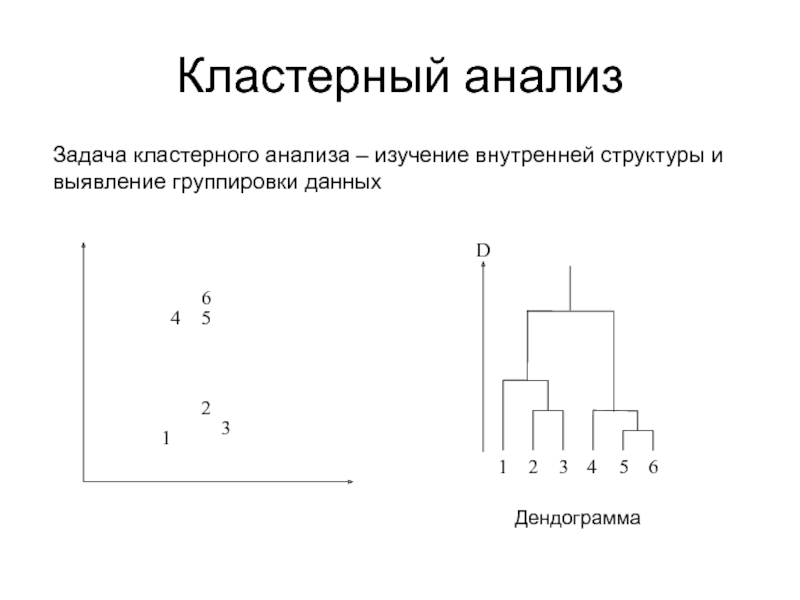
дискриминантном и кластерном анализах
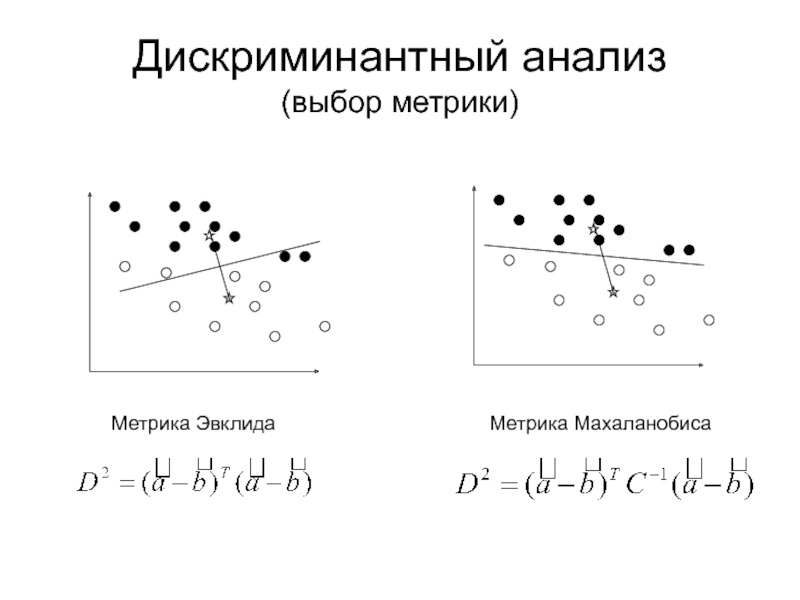
Метрика дескрипторного пространства. Коллинеарные и ортогональные дескрипторы
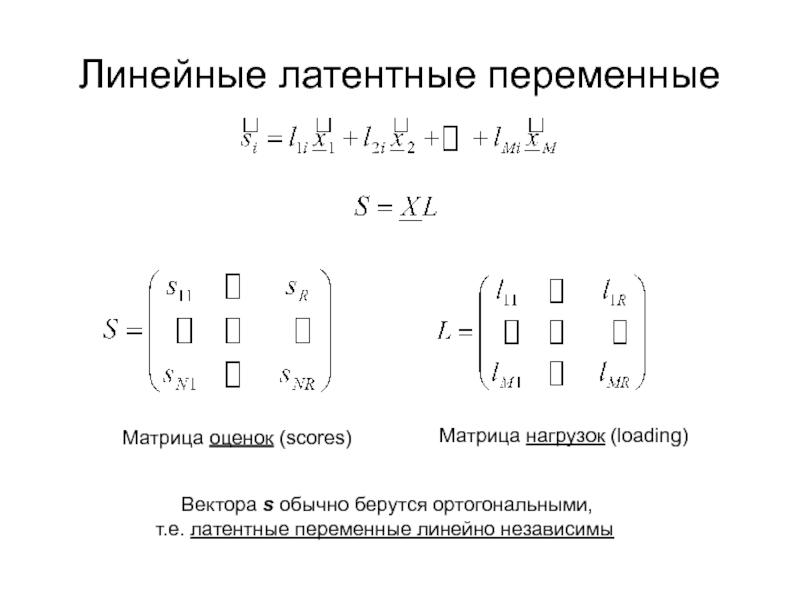
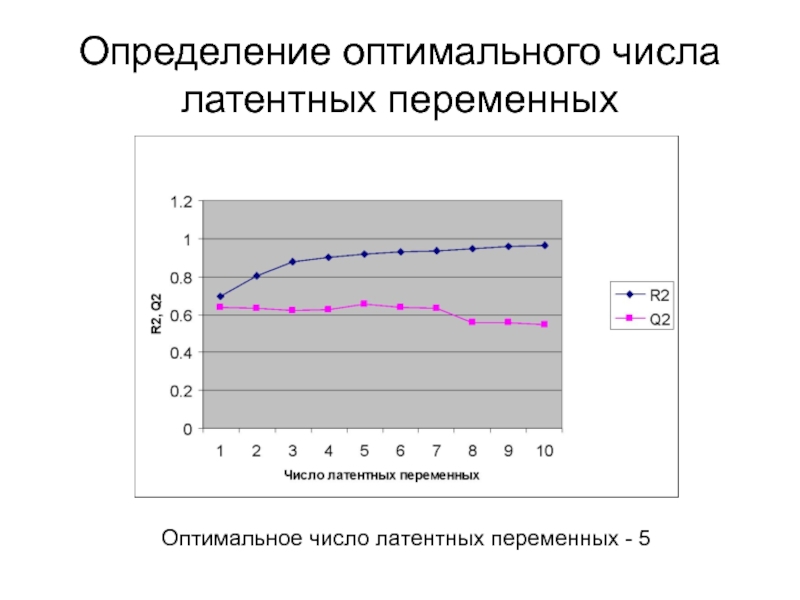
Латентные
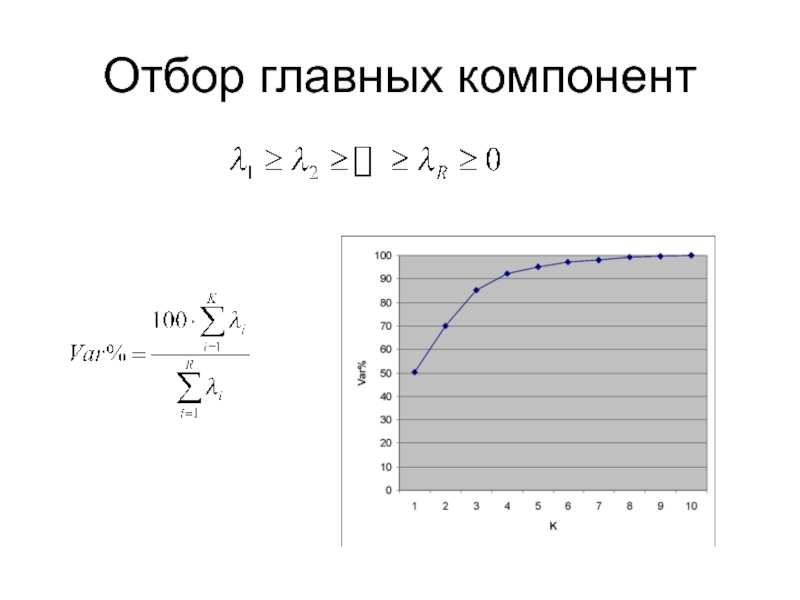
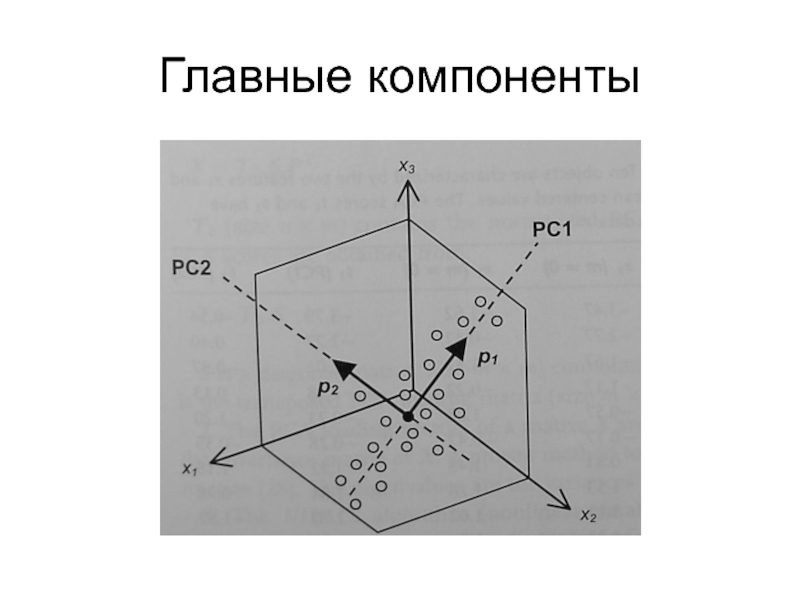
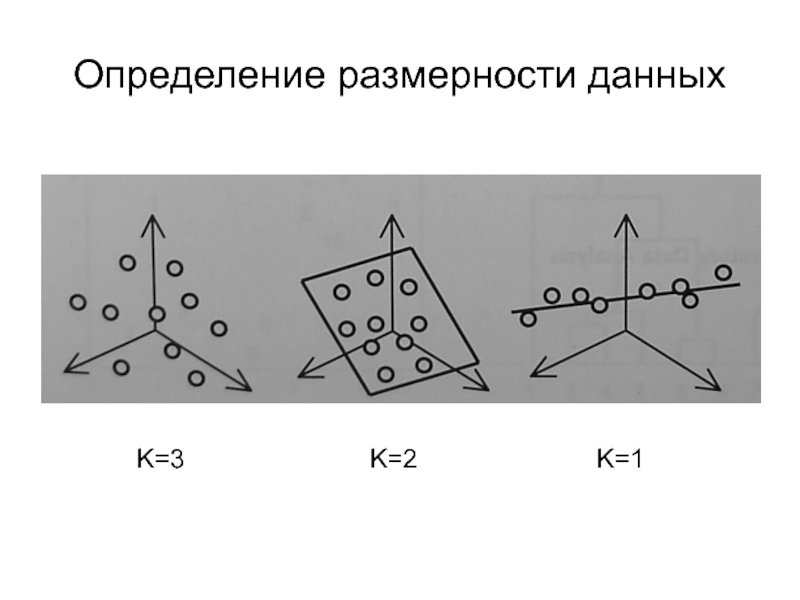
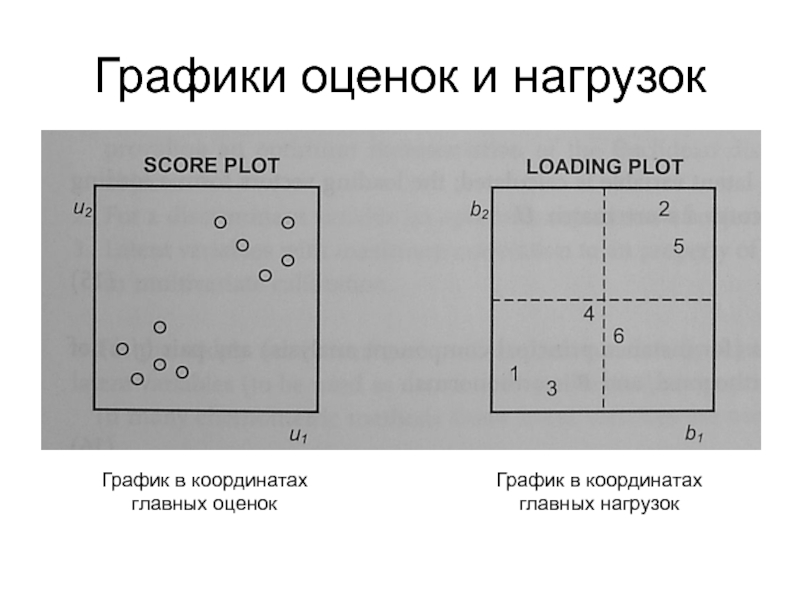
дескрипторы, оценки (scores) и нагрузки (loading)Понятие о факторном анализе и методе главных компонент (PCA)
Метод частичных наименьших квадратов (PLS)