Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхность раздела твердое тело-жидкость
Содержание
- 1. Поверхность раздела твердое тело-жидкость
- 2. Поверхность раздела т-жРис. 1. Различные формы капли
- 3. Поверхность раздела т-жСмачивание- поверхностное явление, заключающееся во
- 4. Поверхность раздела т-жРис.2. Равновесие капли на поверхности
- 5. Слайд 5
- 6. Поверхность раздела т-жКраевой угол θ отсчитывают в
- 7. Поверхность раздела т-жВ правую часть уравнения
- 8. Поверхность раздела т-жНа основе закона Юнга построена
- 9. Поверхность раздела т-жСмачивание ( θ < 90
- 10. Поверхность раздела т-жПолное смачивание или растекание (
- 11. Поверхность раздела т-жХарактер смачивания водой данной поверхности
- 12. Поверхность раздела т-жИспользование уравнения Юнга для расчета
- 13. Поверхность раздела т-ж1. Использование молекулярной теории поверхностного
- 14. Поверхность раздела т-жДля жидкостей, у которых поверхностное
- 15. Поверхность раздела т-жИспользование правила Антонова. Правило Антонова
- 16. Поверхность раздела т-ж1. σ тж = σ
- 17. Зависимость смачиваемости от свойств твердой поверхности Влияние
- 18. Зависимость смачиваемости от свойств твердой поверхностиТак как
- 19. Зависимость смачиваемости от свойств твердой поверхностиИз уравнения
- 20. Зависимость смачиваемости от свойств твердой поверхностиДля сильно
- 21. Состояние ВенцеляРастекание капли на шероховатой поверхности будет
- 22. Состояние ВенцеляРассматривая разность энергий при сдвиге линии
- 23. Состояние КассиПри исследовании многих естественных и микротекстурированных
- 24. Состояние КассиЭнергия границы раздела фаз жидкость-газ намного
- 25. Состояние Касси (Кассье)Впервые такая модель была предложена
- 26. Состояние КассиМикротекстурированная поверхность. Модель Касси.
- 27. Состояние Касси-ВенцеляБыло показано, что для шероховатых и
- 28. Состояние Касси-ВенцеляСуществование метастабильного состояния Касси и устойчивого состояния Венцеля на одной и той же поверхности
- 29. Состояние Касси-ВенцеляОсновные состояния капли на сверхгидрофобной поверхности:
- 30. Состояние Касси-ВенцеляНа рис. показаны два основных типа
- 31. Влияние химической неоднородности поверхностиУравнение Юнга для неоднородной
- 32. Устойчивость состояния Касси (Кассье)Определим, от чего зависит
- 33. Устойчивость состояния Касси (Кассье)
- 34. Устойчивость состояния Касси (Кассье)Однако, было показано, что
- 35. Устойчивость состояния Касси (Кассье)Для описания устойчивости метастабильного
- 36. Устойчивость состояния Касси (Кассье)На основании данного уравнения
- 37. Устойчивость состояния Касси (Кассье)Экспериментально переход из состояния
- 38. Закон Кассье Закон Кассье определяет эффективное значение
- 39. Слайд 39
- 40. Слайд 40
- 41. Гистерезис смачиванияЗависимость краевых углов от условий их
- 42. Гистерезис смачиванияПри растекании жидкости по твердой поверхности
- 43. Гистерезис смачиванияПри смачивании в среде газа различают
- 44. Гистерезис смачивания
- 45. Гистерезис смачивания
- 46. Гистерезис смачивания
- 47. Гистерезис смачивания
- 48. Слайд 48
- 49. Гистерезис смачивания
- 50. Гистерезис смачиванияВлияние деформаций. Фактором, осложняющим смачивание являются
- 51. Влияние деформацийr2= r/cosα , r1= r/cosβ. σжг·
- 52. Гистерезис смачивания
- 53. Смачивание нанокаплями Для небольших капель существенную роль
- 54. Смачивание нанокаплямиИзбыточную энергию линии трехфазного контакта по
- 55. Смачивание нанокаплямикоторое действует по нормали к линии
- 56. Смачивание нанокаплями.Обычно линейное натяжение составляет не более
- 57. Смачивание нанокаплямиЛинейное натяжение как фундаментальное понятие термодинамики
- 58. Смачивание нанокаплямиЛинейное натяжение следует учитывать при расчете
- 59. Растекание жидкости.Капля жидкости, нанесенная на поверхность, может
- 60. Растекание жидкостиДля самопроизвольного процесса dG0 (условие растекания)
- 61. Растекание жидкостиРастекание происходит тогда, когда работа адгезии
- 62. Классические законы смачивания
- 63. Переход смачиванияПереход смачивания - переход из состояния
- 64. Тепловой эффект смачивания Тепловой эффект смачивания обусловлен
- 65. Тепловой эффект смачивания Различают дифференциальную и интегральную
- 66. Тепловой эффект смачивания Интегральная теплота смачивания λi
- 67. Тепловой эффект смачивания Теплоты смачивания используют для
- 68. Спасибо за внимание!
- 69. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Поверхность раздела т-ж
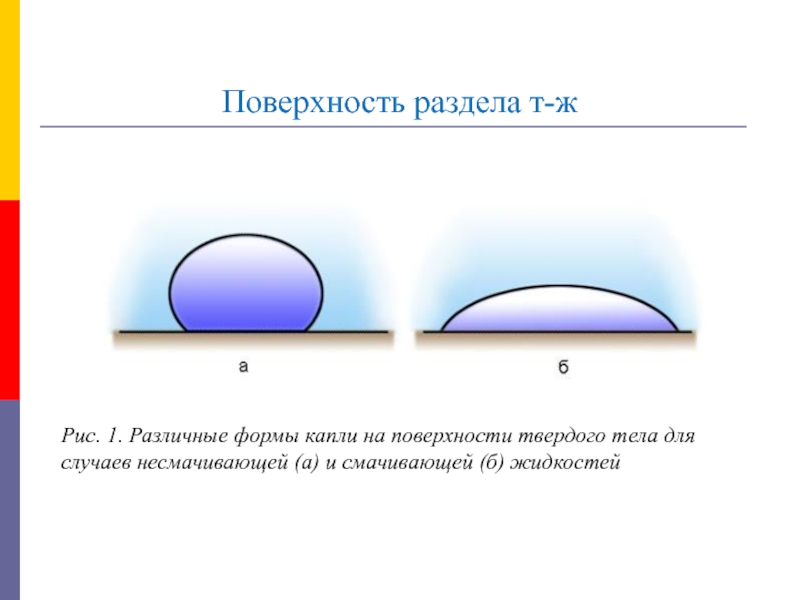
Рис. 1. Различные формы капли на поверхности твердого
тела для случаев несмачивающей (а) и смачивающей (б) жидкостей
Слайд 3Поверхность раздела т-ж
Смачивание- поверхностное явление, заключающееся во взаимодействии жидкости с
твердым или другим жидким телом при наличии одновременного контакта трех
несмешивающихся фаз, одна из которых обычно является газом (воздух).Количественной характеристикой смачивания служит краевой угол смачивания, который измеряется по наклону касательной к поверхности капли, находящейся на твердой поверхности. Вершина краевого угла лежит на линии контакта всех трех фаз, участвующих в смачивании. Общую границу называют линией смачивания, или линией трехфазного контакта.
Степень смачивания – характеризуется краевым углом смачивания.
Слайд 4Поверхность раздела т-ж
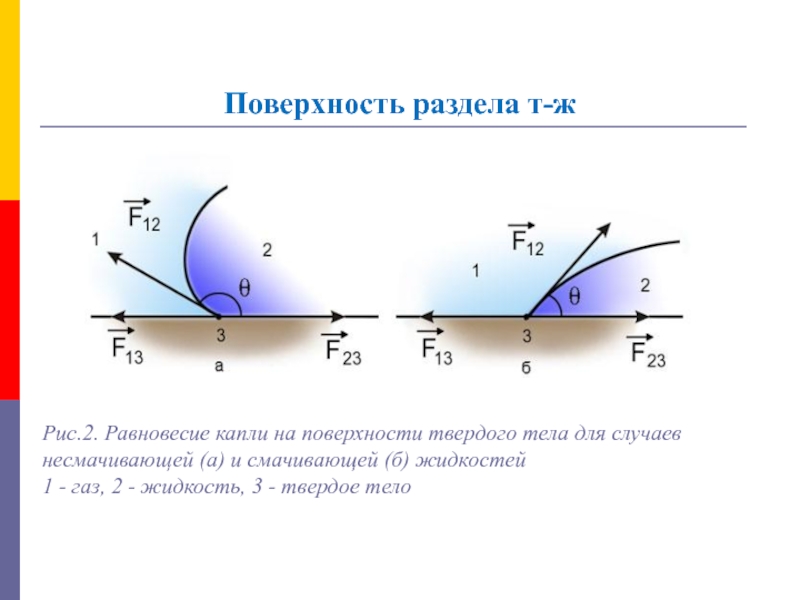
Рис.2. Равновесие капли на поверхности твердого тела для
случаев несмачивающей (а) и смачивающей (б) жидкостей 1 - газ,
2 - жидкость, 3 - твердое телоСлайд 6Поверхность раздела т-ж
Краевой угол θ отсчитывают в сторону смоченной поверхности.
При избирательном смачивании краевой угол отсчитывают в сторону более полярной
жидкости. Краевой угол θ определяется законом Юнга (1804).Слайд 7Поверхность раздела т-ж
В правую часть уравнения входят три параметра
:
удельные поверхностные энергии твердого тела на границе с газом
(σтг) и жидкостью (σтж) и поверхностное натяжение жидкости на границе с газом (σжг). Все три параметра являются термодинамическими.
Поэтому каждой трехфазной системе соответствует ( при определенной температуре Т) единственное значение краевого угла.
При избирательном смачивании закон Юнга имеет вид:
Cos θ = σтж1 - σтж2/ σж1ж2 (5.6)
Где σтж1– удельная поверхностная энергия на границе твердого тела с жидкостью 1; и σтж2 –удельная поверхностная энергия на границе твердого тела со смачивающее жидкостью 2; σж1ж2 – поверхностное натяжение на границе жидкость1 -жидкость .
Слайд 8Поверхность раздела т-ж
На основе закона Юнга построена классификация различных случаев
контактного взаимодействия жидкостей с поверхностью твердых тел.
Несмачивание ( θ >
90 о). В этом случае удельная поверхностная энергия σ тж на границе твердого тела с жидкостью больше, чем на границе твердого тела с газом
(σ тж > σ тг).
Физический смысл этого неравенства заключается в том, что самопроизвольное растекание жидкости по данной твердой поверхности термодинамически невозможно.
Из закона Юнга следует, что в случае σ тж > σ тг имеем соs θ < 0, т.е. краевые углы тупые (θ > 90 о) . Поверхности, несмачиваемые водой называются гидрофобными.
Слайд 9Поверхность раздела т-ж
Смачивание ( θ < 90 о).
При
смачивании поверхностная энергия σ тж на границе жидкости с
твердой поверхностью меньше, поверхностной энергии σ тг на границе твердое тело –газ (σ тж < σ тг).Тогда, в соответствии с законом Юнга, имеем соs θ > 0, т.е. краевые углы острые.
При условии (σ тг – σ тж ) < σ жг, краевой угол изменяется в интервале 0о<θ<90о.
Смачиваемые поверхности называют лиофильными (гидрофильные).
Слайд 10Поверхность раздела т-ж
Полное смачивание или растекание ( θ = 0
о).
Этот случай реализуется при выполнении условия
σ тг >
(σ тж + σ жг). Это означает, что равновесный краевой угол сформироваться не может.
При этом условии капля растекается по твердой поверхности и превращается в плоскую тонкую пленку.
Толщина смачивающих пленок обычно составляет 1-10 нм.
Пример полного смачивания – ртуть в контакте с неокисленной поверхностью цинка или свинца.
Слайд 11Поверхность раздела т-ж
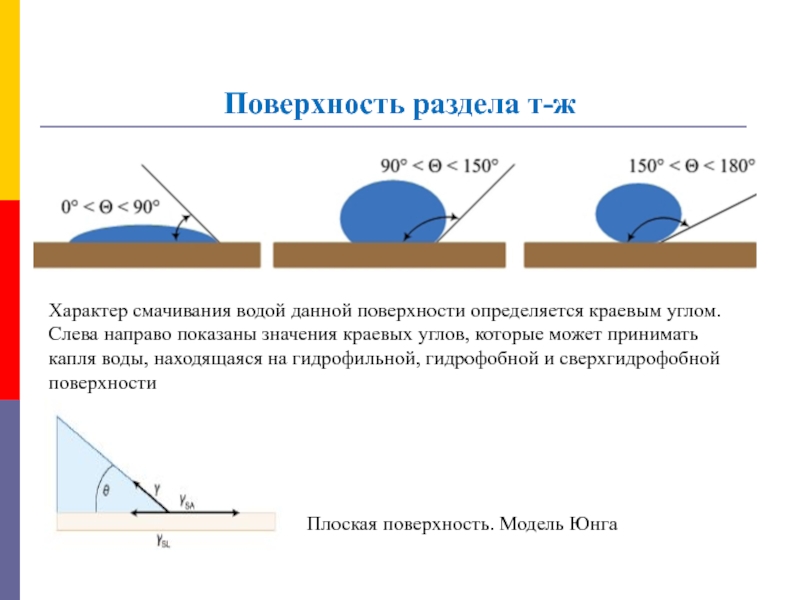
Характер смачивания водой данной поверхности определяется краевым углом.
Слева направо показаны значения краевых углов, которые может принимать капля
воды, находящаяся на гидрофильной, гидрофобной и сверхгидрофобной поверхностиПлоская поверхность. Модель Юнга
Слайд 12Поверхность раздела т-ж
Использование уравнения Юнга для расчета равновесных краевых углов
θ требует сведений об удельных поверхностных энергиях σ тг и
σ тж на границе данного твердого тела с газом и со смачивающей жидкостью .По определенным причинам поверхностные энергии большинства твердых тел не удается измерить достаточно точно.
В связи с этим, в современной теории смачивания применяют способы, которые позволяют это преодолеть . Рассмотрим два таких способа.
Слайд 13Поверхность раздела т-ж
1. Использование молекулярной теории поверхностного натяжения.
Поверхностную энергию
σ тж можно рассчитать с помощью уравнения Фоукса . Для
контакта жидкости с поверхностью его записывают в следующем виде:σтж = σт + σж -2(σт,d ·σж,d)1/2 (1)
Подставив уравнение (1) в уравнение Юнга получаем :
Cos θ = [2(σт,d ·σж,d)1/2/ σж] -1 (2)
Слайд 14Поверхность раздела т-ж
Для жидкостей, у которых поверхностное натяжение создается главным
образом дисперсионными силами (органические вещества, сжиженные, инертные газы), получаем :
Cos
θ = 2{ σт,d/ σж,d}1/2 -1 (3)Таким образом, краевые углы можно рассчитать теоретически , если известны дисперсионные составляющие σт,d и σж,d для твердых тел и жидкостей, соответственно.
Слайд 15Поверхность раздела т-ж
Использование правила Антонова.
Правило Антонова связывает поверхностное натяжение
σ12 на границе двух несмешивающихся жидкостей 1 и 2 с
их поверхностными натяжениями σ1 и σ2 на границе с газом: σ12 = σ1- σ2.Основное условие выполнения правила Антонова - граничащие жидкости не должны растворяться друг в друге или химически взаимодействовать.
При выполнении этих условий правило Антонова применимо и для контакта жидкости с твердой поверхностью. Для таких систем возможно 2 случая:
Слайд 16Поверхность раздела т-ж
1. σ тж = σ т – σ
ж (при σ т > σ ж);
после подстановки этого
выражения для удельной поверхности энергии σтж в уравнение Юнга при σт >σ ж, получаем:Cos θ=1, т.е. происходит полное смачивание.
2. σтж = σ ж – σ т (при σ т < σ ж);
в этом случае подстановка в уравнение Юнга σтж дает
Cosθ = (2 σт / σж) -1 (4)
Уравнение 4 хорошо согласуется с рядом эксперимен-тальных данных: для одной и той же твердой поверхности, контактирующей с разными жидкостями, значения Cosθ растут линейно в зависимости от величины 1/ σж.
Тангенс угла наклона этих прямых равен поверхностной энергии твердых тел.
Слайд 17Зависимость смачиваемости от свойств твердой поверхности
Влияние шероховатости поверхности.
Основное
следствие шероховатости заключается в том,
что площадь такой поверхности Sш
будет больше, чем площадь идеальной гладкой подложки Sи. Отношение Sш/ Sи =К называют коэффициентом шероховатости.
Исходя из определения, К>1 и характеризует отношение фактической площади поверхности к ее проекции на горизонтальную плоскость.
Влияние шероховатости поверхности легко учесть при условии, что размер капли значительно больше среднего размера впадин и выступов на поверхности.
Слайд 18Зависимость смачиваемости от свойств твердой поверхности
Так как в уравнении Юнга
составляющие поверхностного натяжения на границе с твердым телом будут в
К раз больше, то можно записать:К(σ3,1 – σ2,3) = σ2,1 · Cosθш
Если это уравнение разделить на уравнение Юнга, получим:
К= Cosθш/ Cosθ (5)
Это уравнение получило название уравнения Венцеля-Дерягина.
Так как К>1 (всегда) , то │ Cosθш│> │ Cosθ│.
Слайд 19Зависимость смачиваемости от свойств твердой поверхности
Из уравнения (5) следует:
при смачивании
Cosθ>0, поэтому, шероховатость, увеличивая Cosθш, уменьшает угол смачивания, т.е. смачивание
улучшается;если Cosθ<0,(лиофобная поверхность), то шероховатость, увеличивая отрицательную величину Cosθш, способствует росту угла смачивания,
т.е. смачивание ухудшается.
Слайд 20Зависимость смачиваемости от свойств твердой поверхности
Для сильно шероховатых поверхностей равновесный
КУ отличается от КУ для плоских поверхностей того же химического
состава и не соответствует значению, полученному из уравнения Юнга.Венцелем была предложена модель для описания смачивания шероховатых поверхностей.
Слайд 21Состояние Венцеля
Растекание капли на шероховатой поверхности будет происходить до равновесного
состояния, которое не будет описываться уравнением Юнга.
В случае смачивания
шероховатой поверхности реальная площадь контакта будет больше видимой в r раз, работа энергия границы раздела фаз той же площади также будет отличатьсяв r раз. Равновесное состояние в этом случае называют «состоянием Венцеля».
Слайд 22Состояние Венцеля
Рассматривая разность энергий при сдвиге линии трехфазного контакта на
малую величину (рис.), можно получить выражение для макроскопического равновесного краевого
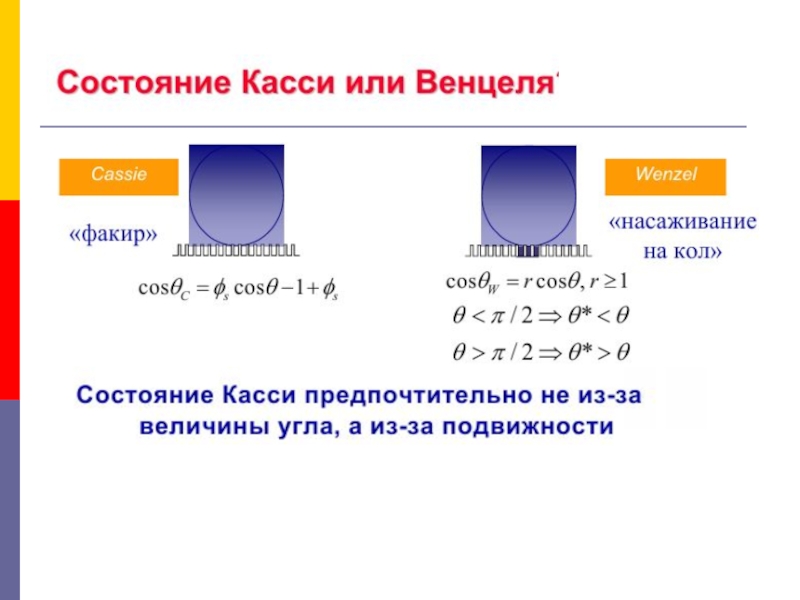
угла, характеризующего состояние Венцеля:cos θВ = r cos θю
Шероховатая поверхность. Модель Венцеля
Слайд 23Состояние Касси
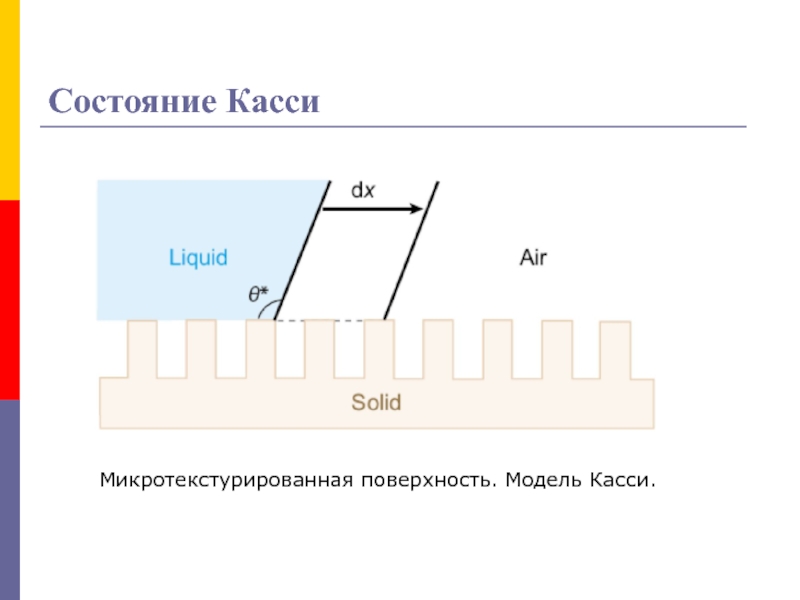
При исследовании многих естественных и микротекстурированных гидрофобных поверхностей было
показано, что при смачивании таких поверхностей внутри полостей их рельефа
устойчивы пузырьки воздуха.Т.е. фактически жидкость расположена на своеобразной воздушной подушке.
Слайд 24Состояние Касси
Энергия границы раздела фаз жидкость-газ намного меньше энергии границы
твердое-жидкость,
поэтому краевой угол при смачивании таких поверхностей также будет
сильно отличаться от краевого угла Юнга и будет зависеть от соотношения площадей контактов жидкость-газ и жидкость-твердое тело в видимом контакте жидкости с поверхностью.
Слайд 25Состояние Касси (Кассье)
Впервые такая модель была предложена Касси и Бакстером
.
Равновесное состояние в этом случае называют «состоянием (или «состоянием
Касси-Бакстера»). Рассматривая разность энергий при сдвиге линии трехфазного контакта на малую величину (рис.), можно получить выражение для макроскопического равновес-ного краевого угла, характеризующего состояние Касси:
cos θк = −1 + (1 − σтв) cos θю,
Слайд 27Состояние Касси-Венцеля
Было показано, что для шероховатых и текстурированных поверхностей существует
два основных режима смачивания:
состояние Венцеля, в котором все полости
рельефа поверхности заполнены жидкостью, и граница раздела фаз действительно представляет собой раздел фаз жидкость-твердое, и состояние Касси, в котором внутри полостей рельефа поверхности стабилизированы пузырьки газа, и видимый контакт жидкость-твердое, на самом деле, представляет собой гетерогенную границу раздела фаз жидкость-твердое-газ.
Слайд 28Состояние Касси-Венцеля
Существование метастабильного состояния Касси и устойчивого состояния Венцеля на
одной и той же поверхности
Слайд 29Состояние Касси-Венцеля
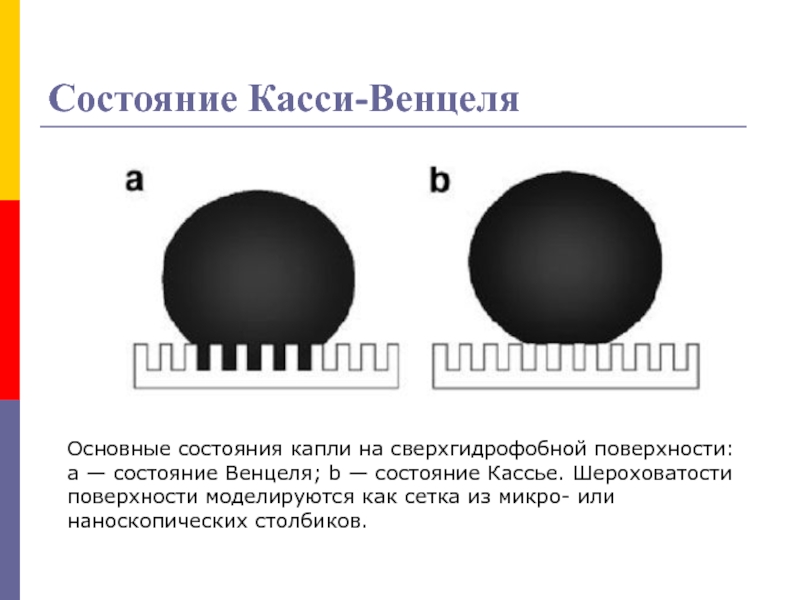
Основные состояния капли на сверхгидрофобной поверхности:
а — состояние
Венцеля; b — состояние Кассье. Шероховатости поверхности моделируются как сетка
из микро- или наноскопических столбиков.Слайд 30Состояние Касси-Венцеля
На рис. показаны два основных типа расположения капли на
сверхгидрофобной шероховатой поверхности: состояние Венцеля (рис. а) и состояние Кассье
(рис. b).В состоянии Венцеля капля частично смачивает шероховатые области, и поэтому заполняет их водой.
В состоянии Кассье капля не реагирует на рельеф поверхности и не смачивает участки с шероховатостями, имея меньшую площадь контакта.
Слайд 31Влияние химической неоднородности поверхности
Уравнение Юнга для неоднородной бинарной твердой поверхности:
Cosθн
= ψCosθА + (1-ψ) CosθВ (8)
Где θА и
θВ – краевые углы данной жидкости на однородных твердых поверхностях А и В, соответственно.Ψ- относительная доля площади, занимаемая веществом А
(1-ψ) – доля площади, занимаемая веществом В.
Уравнение (8) называют уравнением Ребиндера-Кассье( 1931, 1946). Оно показывает, что по краевым углам смачивания можно получить информацию о химическом составе поверхности, например, о соотношении площадей, занимаемых полярными и неполярными группами на поверхности биополимеров.
Слайд 32Устойчивость состояния Касси (Кассье)
Определим, от чего зависит устойчивость или неустойчивость
состояния Касси на тех или иных поверхностях.
Для начала рассмотрим
устойчивость состояния Касси с точки зрения энергии, т.е. при каких условиях состояние Касси будет устойчиво термодинамически. Эта устойчивость определяется геометрическими параметрами поверхности r и ϕтв и химией поверхности, т.е. краевым углом Юнга cosθЮ.
Слайд 34Устойчивость состояния Касси (Кассье)
Однако, было показано, что в некоторых случаях
существование состояния Касси наблюдается и при cos θЮ > cos
θкрит.Но т.к. свойства поверхности таковы, что термодинамически устойчиво состояние Венцеля, то различными способами можно вызвать необратимый переход из состояния Касси в состояние Венцеля (ПКВ), а состояние Касси является метастабильным.
Т.к. существуют такие поверхности, на которых возможно сосуществование этих двух состояний, то интересной задачей
было определить
условия перехода из метастабильного состояния Касси в устойчивое состояние Венцеля.
Слайд 35Устойчивость состояния Касси (Кассье)
Для описания устойчивости метастабильного состояния Касси было
предложено несколько подходов.
Первый - основан на модификации уравнения 9 для
микроканала, полностью заполненного жидкостью в процессе перехода газовая фаза полностью замещается жидкостью, поступающей извне. При этом объем жидкости в микроканале увеличивается как раз на величину, равную объему замещенного газа.
Кроме того, важным отличием является учет кривизны мениска (в рассуждениях выше межфазная граница предполагалась плоской, и давление Лапласа не учитывалось).
Тогда условие устойчивости состояния Касси будет выглядеть следующим образом:
(γжг + h∆p) cos θкрит − γ cos θЮ > 0, где h — высота особенностей текстуры (колонн, стенок в зависимости от топологии текстуры), ∆p —разница давлений в жидкости и газовой фазе, зафиксированной внутри полостей текстуры.
Слайд 36Устойчивость состояния Касси (Кассье)
На основании данного уравнения можно оценить давление,
которое будет вызывать переход из неустойчивого равновесного состояние Касси в
устойчивое состояние Венцеля.Также данный переход можно наблюдать для отдельной капли жидкости на супергидрофобной поверхности.
В отличие от заполненного канала, объем капли в процессе перехода сохраняется постоянным, поэтому уравнение становится неприменимо.
Слайд 37Устойчивость состояния Касси (Кассье)
Экспериментально переход из состояния Касси в состояние
Венцеля легче всего наблюдать в процессе испарения капли на поверхности.
Увеличение лапласового давления внутри капли в процессе ее испарения вызывает переход, когда разница давлений достигает определенного значения.
Также ПКВ наблюдается при падении капли , придавливании ее к супергидрофобной поверхности, колебаниях поверхности и др.
Слайд 38Закон Кассье
Закон Кассье определяет эффективное значение угла контакта θc
с жидкостью в случае неоднородной поверхности . Закон объясняет, как
можно увеличить значение контактного угла для поверхности всего лишь придав ей шероховатость. Математическое выражение закона следующее:где θ1 - угол контакта компонента 1, присутствующего в композиционном материале, с долей площади поверхности γ1, а θ2 - угол контакта компонента 2 с долей площади поверхности γ2.
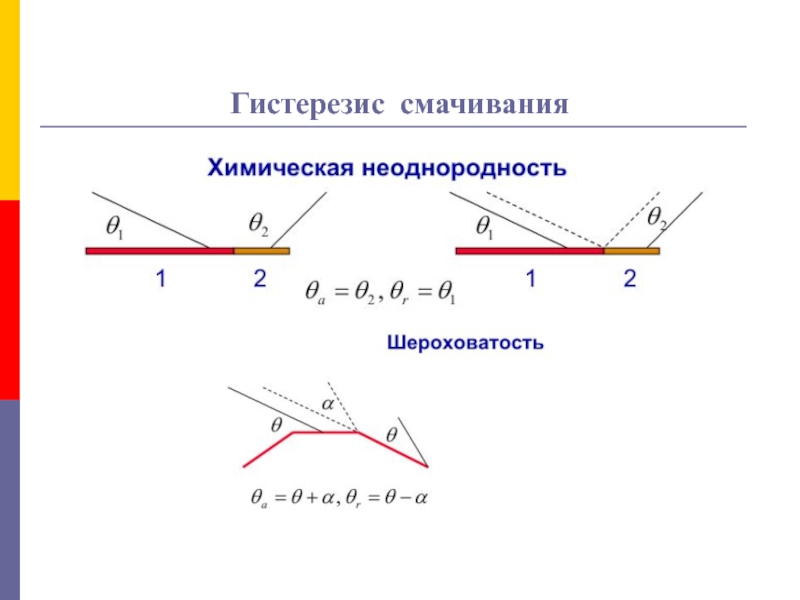
Слайд 41Гистерезис смачивания
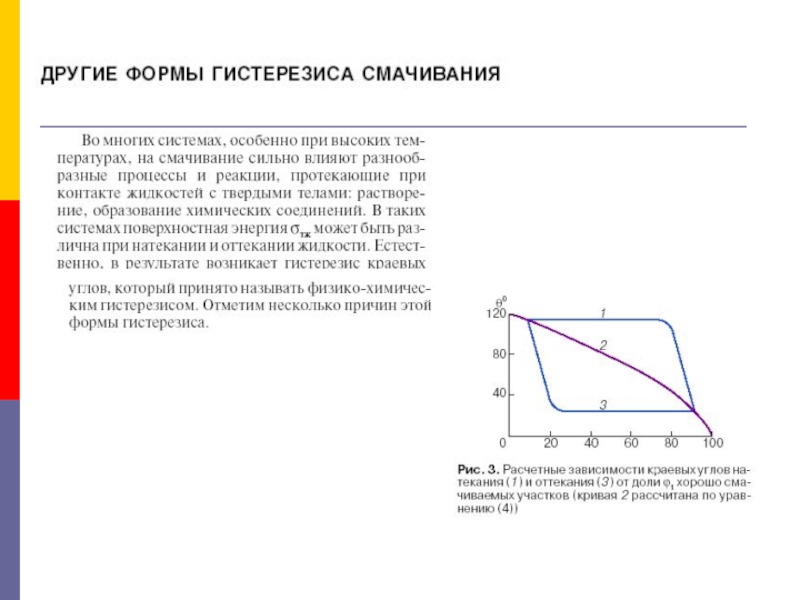
Зависимость краевых углов от условий их формирования называется гистерезисом
смачивания.
Гистерезис смачивания —краевой угол в точке соприкосновения поверхности жидкости с
сухой поверхностью твердого тела имеет величину большую, чем при соприкосновении с поверхностью того же тела, предварительно смоченной.Слайд 42Гистерезис смачивания
При растекании жидкости по твердой поверхности краевой угол не
достигает равновесного значения вследствие гистерезиса смачивания — явления, тормозящего перемещение
периметра смачивания по твердой поверхности. При растекании жидкости по твердой поверхности гистерезисный угол больше равновесного угла смачивания, определяемого по формуле. Установлено, что гистерезис смачивания больше на шероховатых и более гидрофобных поверхностях. После воздействия флотореагентов, гидрофобизирующих поверхность минералов, гистерезис смачивания увеличивается.Слайд 43Гистерезис смачивания
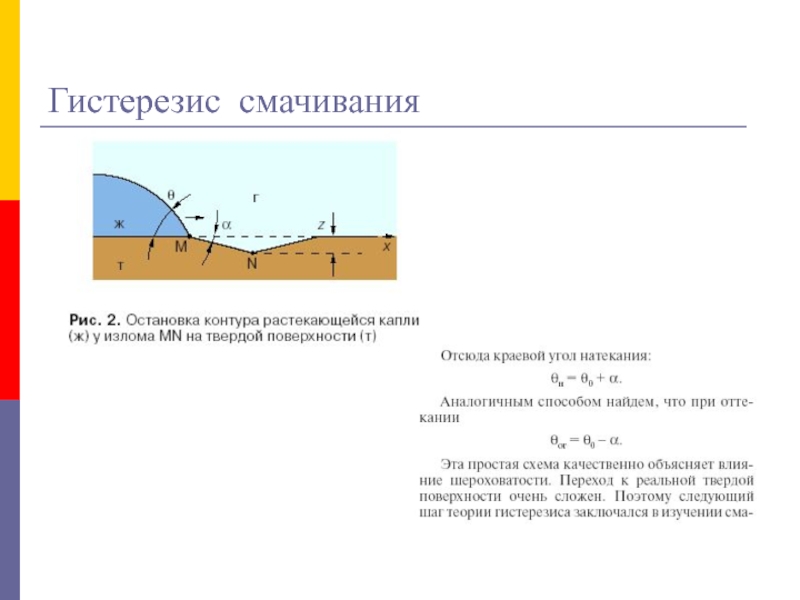
При смачивании в среде газа различают краевые углы натекания
θа и оттекания θr;
θа устанавливается при нанесении капли жидкости
на твердую поверхность (рис. а), θr – при подведении пузырька воздуха к поверхности образца, погруженного в жидкость (рис. б).
Слайд 50Гистерезис смачивания
Влияние деформаций.
Фактором, осложняющим смачивание являются деформационные изменения поверхности
твердого тела при контакте со смачивающей жидкостью.
рс1 = 2σжг/r1
(σж – поверхностное натяжение жидкости, r1 – радиус кривизны поверхности под каплей). рс2 = 2σтж/r2.
Слайд 51Влияние деформаций
r2= r/cosα , r1= r/cosβ.
σжг· cosα = σтж·
cosβ
Механическое равновесие на линии смачивания определяют два уравнения:
σтг = σжг·
cosα + σтж· cosβ (11,а)σжг· sinα = σтж· sinβ (11,б)
Уравнение 11,а следует из баланса сил, действующих в горизонтальной плоскости, а уравнение11,б- из уравнения сил, направленных вертикально.
Краевой угол равен θ= α+β.
Слайд 53Смачивание нанокаплями
Для небольших капель существенную роль играет еще один
термодинамический параметр – линейное натяжение (к, Дж/м).
Физический смысл линейного
натяжения заключается в следующем. Молекулы жидкости, которые находятся на линии смачивания АС(рис.), непосредственно контактируют с молекулами двух соседних фаз (газ и твердое тело).
Поэтому их энергетическое состояние отличается от энергетического состояния молекул жидкости на поверхности капли, где она граничит только с одной фазой – газом.
Слайд 54Смачивание нанокаплями
Избыточную энергию линии трехфазного контакта по сравнению с энергией
поверхности жидкости (для одинакового числа молекул) называют линейным натяжением.
В
отличие от поверхности раздела фаз эту энергию относят не к единице площади , а к единице длины, т.е. размерность линейного натяжения –Дж/метр (Дж/м). Поскольку 1 Дж= 1н·м- линейное натяжение имеет размерность силы – ньютон (Н).
Эта сила направлена вдоль линии смачивания, она создает двумерное давление:
р*=к/r (15)
Слайд 55Смачивание нанокаплями
которое действует по нормали к линии смачивания (см. рис.2,3)
. Соотношение (15) называют уравнением Веселовского- Перцова (1936).
При выводе
закона краевого угла θ для малых капель в уравнение равновесия на линии смачивания необходимо вводить дополнительное слагаемое к/r. С учетом этой поправки равновесный краевой угол θ определяет уравнение Шелудко-Тошева-Платиканова (1980):
Cos θ* = Cos θ – k/σr (16)
Слайд 56Смачивание нанокаплями.
Обычно линейное натяжение составляет не более 10-7 -10-6 мН.
Поэтому влияние поправки к/r становится существенным только для наноразмерных капель радиусом
примерно 1-10 нм. Линейное натяжение играет важную роль только в определенных коллоидно-химических процессах, например, при гетерогенном образовании зародышей новой фазы., конденсации капель на твердой поверхности.
Для достаточно больших (r>0.1 мкм) капель вклад слагаемого к/r становится очень малым и уравнение (16 )принимает обычную форму закона Юнга.
Слайд 57Смачивание нанокаплями
Линейное натяжение как фундаментальное понятие термодинамики поверхностных явлений возникает
при описании механического равновесия и энергетических свойств тонких жидких пленок
и трехфазных систем конечного размера.Линейное натяжение понимается
либо как сила ( χ ), действующая вдоль линейной границы тонкой жидкой пленки или линии трехфазного контакта и стремящаяся сократить (при χ > 0) или увеличить (при χ < 0) длину контактной линии,
либо как удельный (отнесенный к единице контактной линии) избыток свободной энергии (большого термодинамического потенциала) системы χ [Дж/м].
Слайд 58Смачивание нанокаплями
Линейное натяжение следует учитывать при расчете силы адгезии твердых
частиц к межфазной поверхности воздух — вода при флотации .
Существованием избыточного двумерного давления χ/r ; (где r — радиус кривизны контактной линии) объясняют наблюдаемую в экспериментах зависимость контактного угла в области мениска пленки от радиуса пленки- r.
Следует, однако, отметить, что в настоящее время отсутствуют общепризнанные экспериментальные оценки линейного натяжения
Слайд 59Растекание жидкости.
Капля жидкости, нанесенная на поверхность, может оставаться на ее
определенном участке
и система будет находится в равновесии в соответствии
с законом Юнга, или же растекаться на поверхности.
В обоих этих случаях, система переходит в состояние с минимальной энергией Гиббса:
dG = (σ2.1 + σ2.3 – σ3.1)dS (17)
Слайд 60Растекание жидкости
Для самопроизвольного процесса dG0 (условие растекания)
получим:
σ2.1 + σ2.3 – σ3.1 σ2.1 + σ2.3
(18)Из соотношения (18) следует, что уменьшение межфазного натяжения (σ2.3, увеличение работы адгезии) и поверхностного натяжения жидкости σ2.1 способствует растеканию жидкости на поверхности смачиваемого тела.
Слайд 61Растекание жидкости
Растекание происходит тогда, когда работа адгезии превышает работу когезии
растекающейся жидкости.
Разница между этими величинами составляет коэффициент растекания f
по Гаркинсу:f = σ3.1 – σ 2.1 - σ2.3
или f = Wa – Wk
при положительном значении f – жидкость растекается по поверхности, при отрицательном – не растекается.
Слайд 63Переход смачивания
Переход смачивания - переход из состояния частичного смачивания в
состояние полного смачивания.
Может иметь место и в случае жидких
линз, заключенных между двумя несмешивающимися жидкостями. Понятие было введено независимо Каном, Эбнером и Саамом .
Такой переход может происходить при постепенном изменении состава сосуществующих фаз или температуры.
С ростом температуры, при приближении к критической точке, когда межфазная энергия стремиться к нулю.
Слайд 64Тепловой эффект смачивания
Тепловой эффект смачивания обусловлен межмолекулярным взаимодействием на
границе Т/Ж, в результате которого при нанесении жидкости на твердое
тело происходит убыль не только свободной поверхностной энергии, но и полной поверхностной энергии (поверхностной энтальпии).Межмолекулярное взаимодействие тем сильнее, чем меньше разность полярностей жидкости и твердого тела.
Поэтому тепловой эффект смачивания гидрофильных тел водой больше, чем углеводородами и наоборот – для гидрофобных тел он ниже, чем при смачивании их углеводородами.
Слайд 65Тепловой эффект смачивания
Различают дифференциальную и интегральную теплоты смачивания.
Дифференциальная теплота
смачивания λd – теплота, выделяющаяся при нанесении бесконечно малого количества
жидкости на поверхность, уже содержащую некоторое количество жидкости (слой толщиной x).Эта теплота максимальна при x = 0 и убывает до λd = 0 при некоторой толщине x = h, равной расстоянию, на котором интенсивность поля ненасыщенных молекулярных сил поверхности спадает до нуля.
Ее относят к 1 моль смачивающей жидкости: [λd] = Дж/моль.
Слайд 66Тепловой эффект смачивания
Интегральная теплота смачивания λi - теплота, выделяющаяся
при нанесении некоторого конечного количества жидкости x на исходную (сухую)
поверхность:При x → h величина λi возрастает до λi =λmax ,где λmax – полная интегральная теплота смачивания, отвечающая полному заполнению поверхностного слоя с единичной площадью: [λi] = Дж/м2.
Слайд 67Тепловой эффект смачивания
Теплоты смачивания используют для оценки поверхностных молекулярных
свойств тела и количественной характеристики смачиваемости, когда невозможно экспериментально определить
значение краевого угла: в случае порошкоооб-разных, волокнистых, пористых тел.Чтобы избежать измерений межфазной поверхности таких тел, в качестве термической характеристики смачиваемости используют отношение полных теплот смачивания тел водой и углеводородом:
где λH2O и λУ - полная интегральная теплота смачивания водой и углеводородом соответственно, β - термический коэффициент смачивания. Если β > 1, то тело гидрофильно, при β < 1 тело гидрофобно.