Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистика бюджета
Содержание
- 1. Статистика бюджета
- 2. Экономические моделиЭкономические модели позволяют выявить особенности функционирования
- 3. Этапы эконометрического моделирования1-й этап (постановочный). Формулируется цель
- 4. Цели эконометрического моделирования анализ исследуемого экономического объекта (процесса); прогноз его
- 5. Выбор объясняющих переменныхПри выборе экономических переменных необходимо
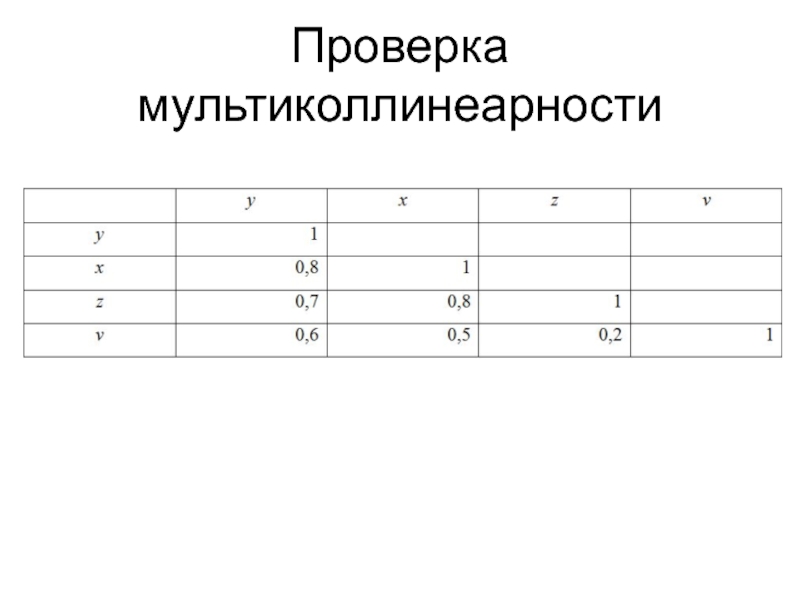
- 6. Проверка мультиколлинеарности
- 7. Теснота связиКоэффициент корреляции;Коэффициент детерминации (квадрат коэффициента корреляции).
- 8. Проверка качества моделиОценка статистической значимости параметров уравнения
- 9. Варианты сочетаний результатовУравнение по F-критерию статистически значимо
- 10. Средняя ошибка аппроксимацииСредняя ошибка аппроксимации – среднее
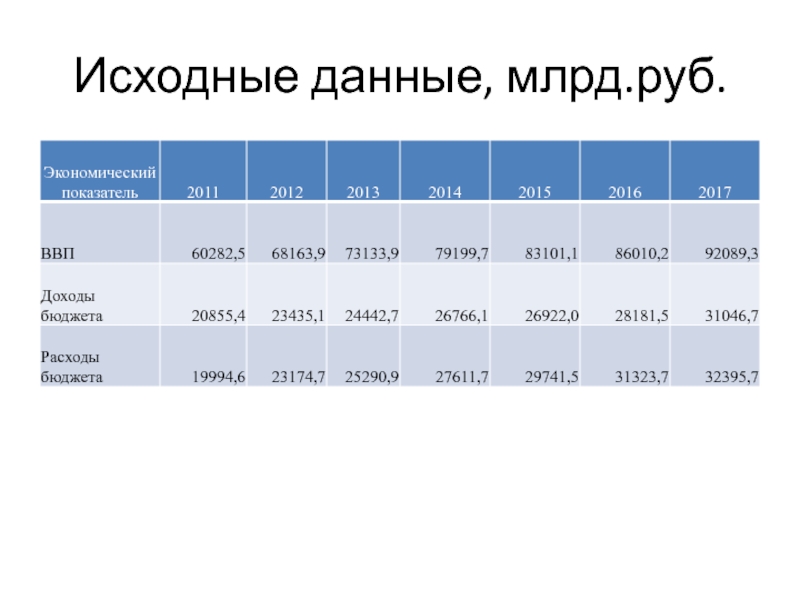
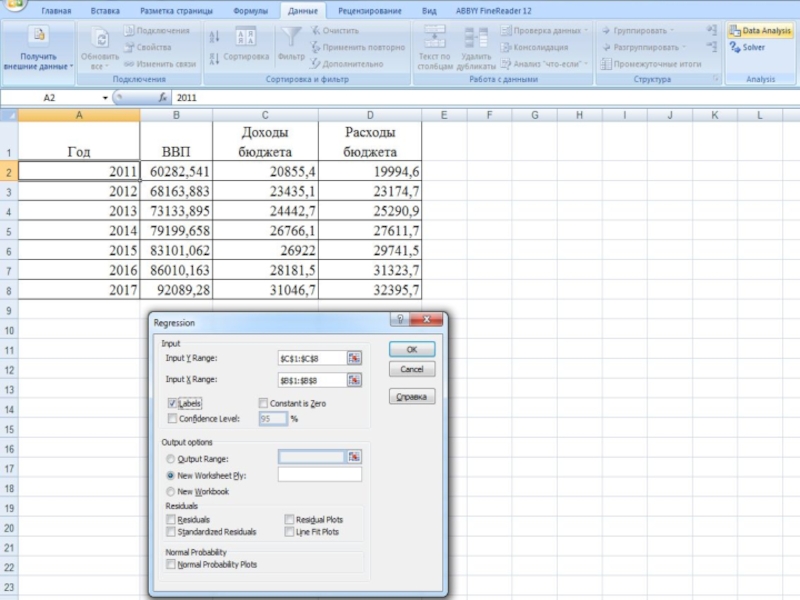
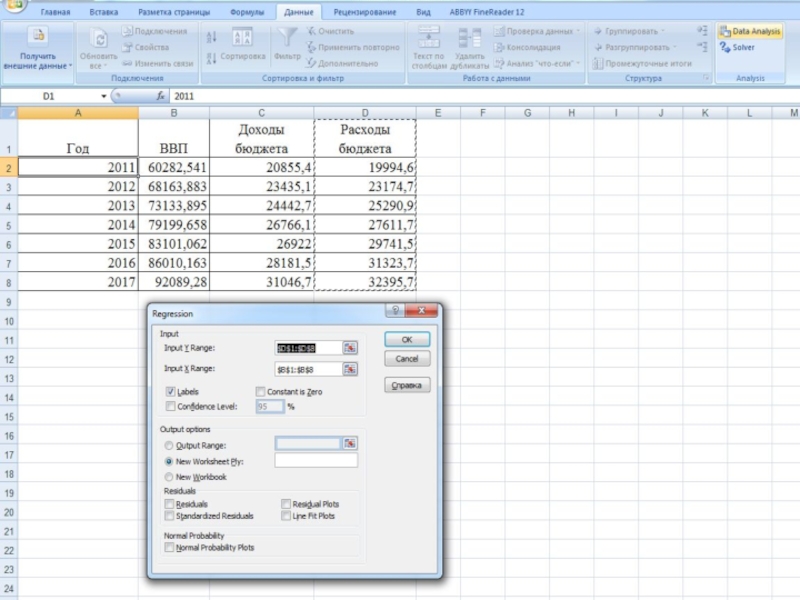
- 11. Исходные данные, млрд.руб.
- 12. Слайд 12
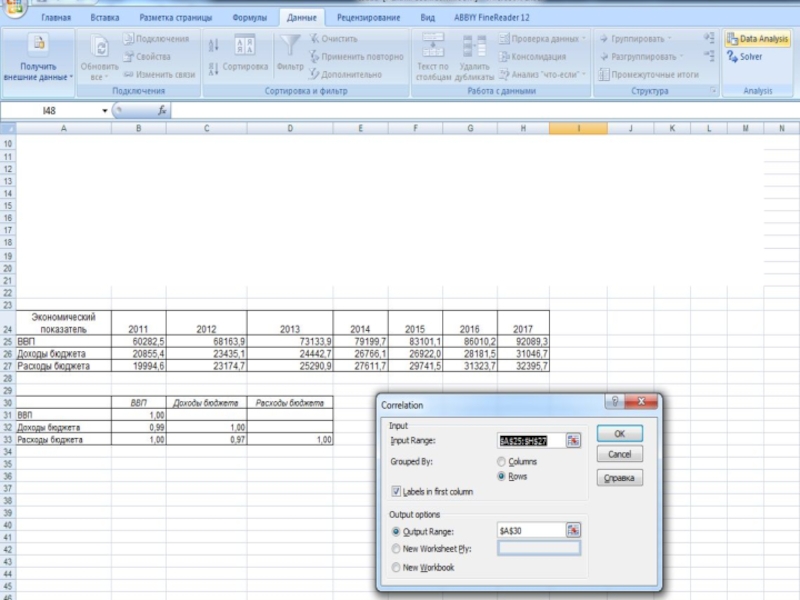
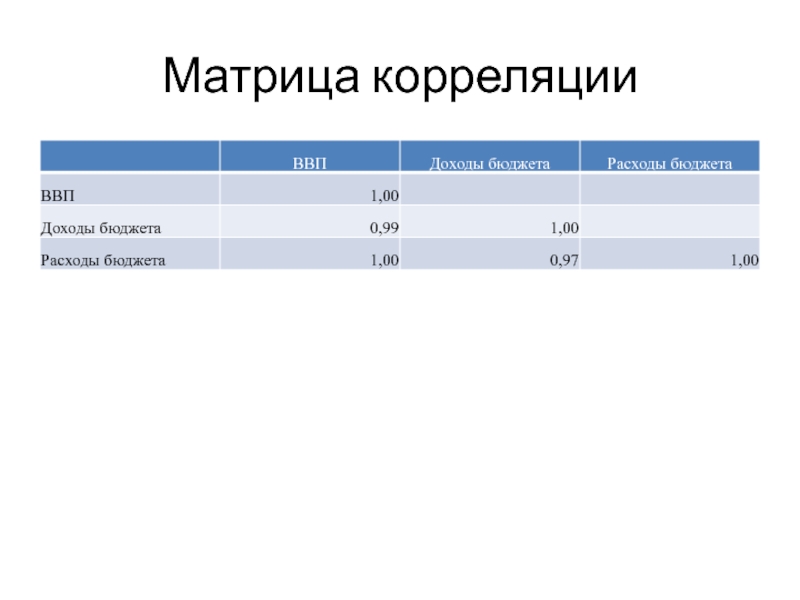
- 13. Матрица корреляции
- 14. Построение однофакторной линейной модели зависимости доходов бюджета от ВВП
- 15. Слайд 15
- 16. Слайд 16
- 17. Интерпретация результатовС увеличением ВВП на 1 млрд.руб.
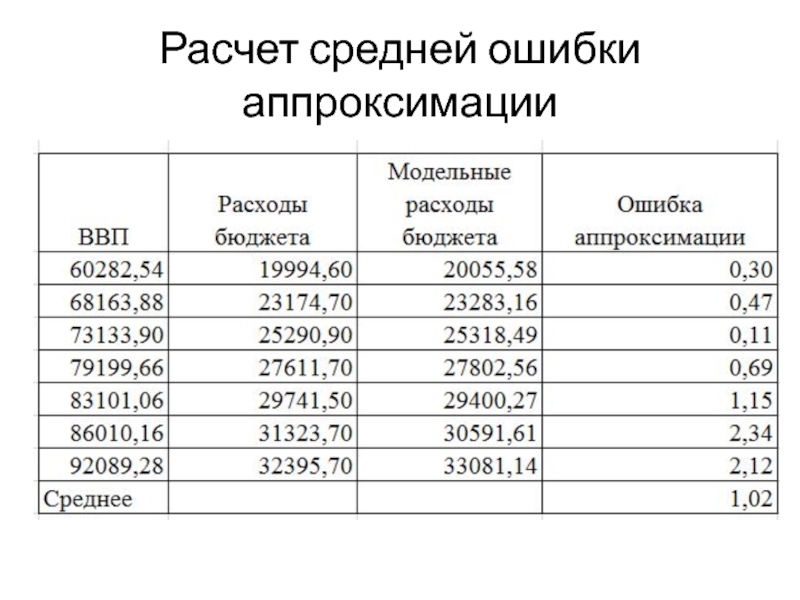
- 18. Расчет средней ошибки аппроксимации
- 19. Вывод о качестве моделиПостроенное уравнение регрессии считается
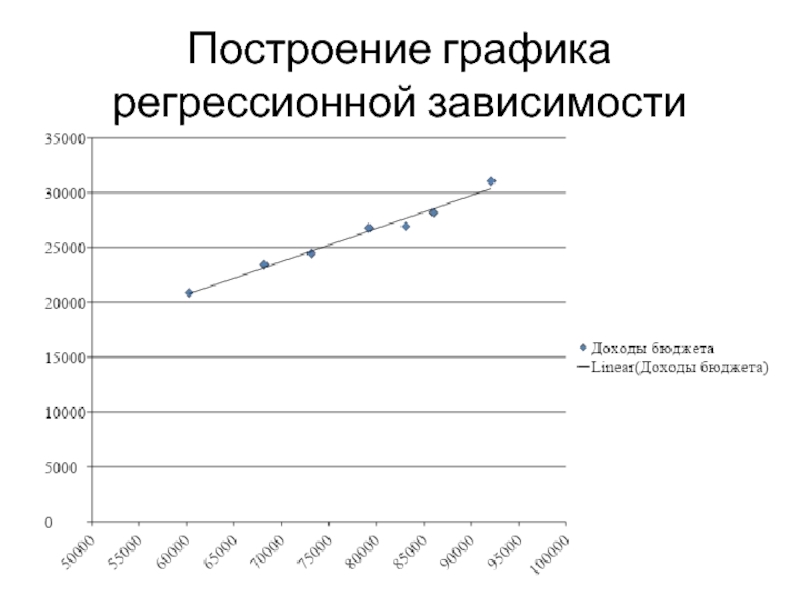
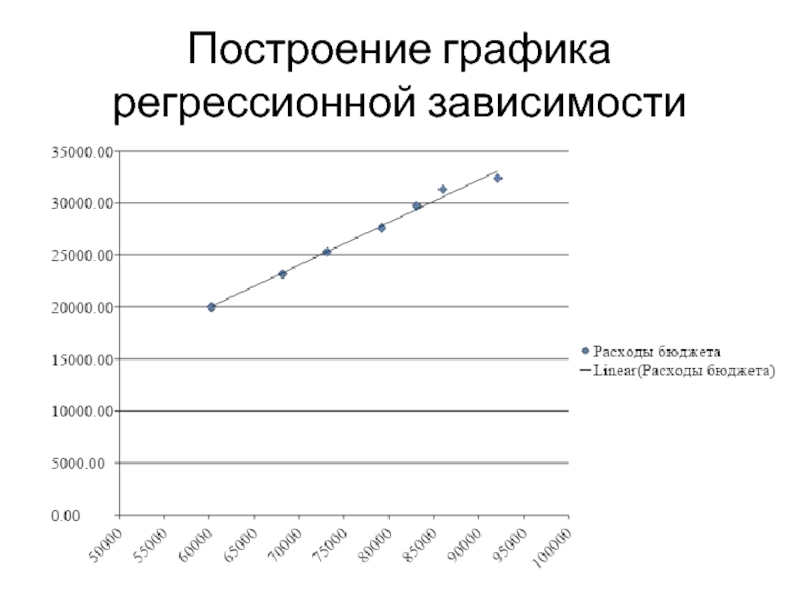
- 20. Построение графика регрессионной зависимости
- 21. Сравнение функций
- 22. Построение однофакторной линейной модели зависимости расходов бюджета от ВВП
- 23. Слайд 23
- 24. Слайд 24
- 25. Расчет средней ошибки аппроксимации
- 26. Построение графика регрессионной зависимости
- 27. Построение двухфакторной линейной модели зависимости доходов бюджета от ВВП и финансовых результатов хозяйствующих субъектов
- 28. Матрица корреляции
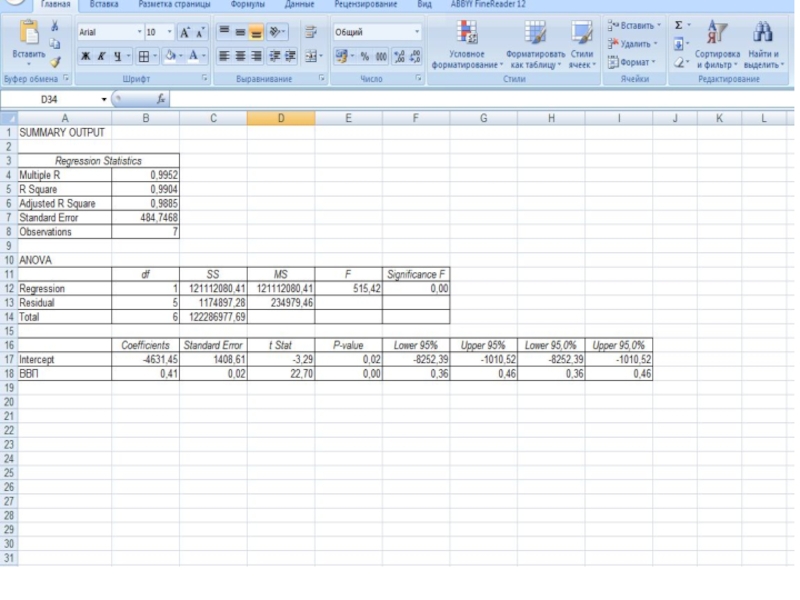
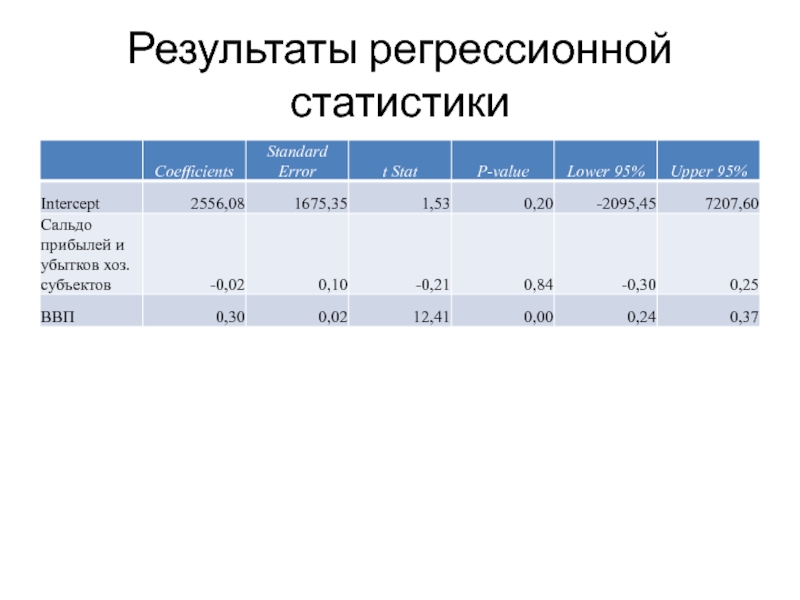
- 29. Результаты регрессионной статистики
- 30. Благодарю за внимание!
- 31. Скачать презентанцию
Экономические моделиЭкономические модели позволяют выявить особенности функционирования экономического объекта и на основе этого предсказать будущее поведение объекта при изменении каких-либо параметров. В модели все взаимосвязи переменных могут быть оценены количественно, что
Слайды и текст этой презентации
Слайд 2Экономические модели
Экономические модели позволяют выявить особенности функционирования экономического объекта и
Слайд 3Этапы эконометрического моделирования
1-й этап (постановочный). Формулируется цель исследования, набор участвующих
в модели экономических переменных.
2-й этап (априорный). Проводится анализ сущности изучаемого
объекта, формирование и формализация априорной (известной до начала моделирования) информации.3-й этап (параметризация). Осуществляется непосредственное моделирование, т.е. выбор общего вида модели, выявление входящих в нее связей. Основная задача, решаемая на этом этапе, – выбор вида регрессионной функции f(x) в экономической модели.
4-й этап (информационный). Осуществляется сбор необходимой статистической информации – наблюдаемых значений эконометрических переменных. Здесь могут быть наблюдения, полученные как с участием исследователя, так и без его участия.
5-й этап (идентификация модели). Осуществляется статистический анализ модели и оценка ее параметров.
6-й этап (верификация модели). Проводится проверка истинности, адекватности модели.
Слайд 4Цели эконометрического моделирования
анализ исследуемого экономического объекта (процесса);
прогноз его экономических показателей, имитация развития объекта
при различных значениях экзогенных переменных (отражая их случайный характер, изменение
во времени);выработка управленческих решений.
Слайд 5Выбор объясняющих переменных
При выборе экономических переменных необходимо теоретическое обоснование каждой
переменной (при этом рекомендуется, чтобы число их было не очень
большим и, как минимум, в 7 раз меньше числа наблюдений).Объясняющие переменные не должны быть связаны функциональной или тесной корреляционной зависимостью, т.к. это может привести к невозможности оценки параметров модели или к получению неустойчивых, не имеющим реального смысла оценок, т.е. к явлению мультиколлинеарности.
Слайд 7Теснота связи
Коэффициент корреляции;
Коэффициент детерминации (квадрат коэффициента корреляции).
Слайд 8Проверка качества модели
Оценка статистической значимости параметров уравнения осуществляется на основе t-статистики
Стьюдента.
Для проверки значимости модели регрессии используется F-критерий Фишера.
Слайд 9Варианты сочетаний результатов
Уравнение по F-критерию статистически значимо и все параметры
уравнения по t-статистике тоже статистически значимы. Данное уравнение может быть
использовано как для принятия управленческих решений, так и для прогнозирования.По F-критерию уравнение статистически значимо, но незначимы отдельные параметры уравнения. Уравнение может быть использовано для принятия управленческих решений, касающихся управления теми факторами, по которым получено подтверждение статистической значимости, но уравнение не может быть использовано для прогнозирования.
Уравнение по F-критерию статистически значимо, но незначимы все параметры уравнения. Уравнение не следует использовать ни для каких целей.
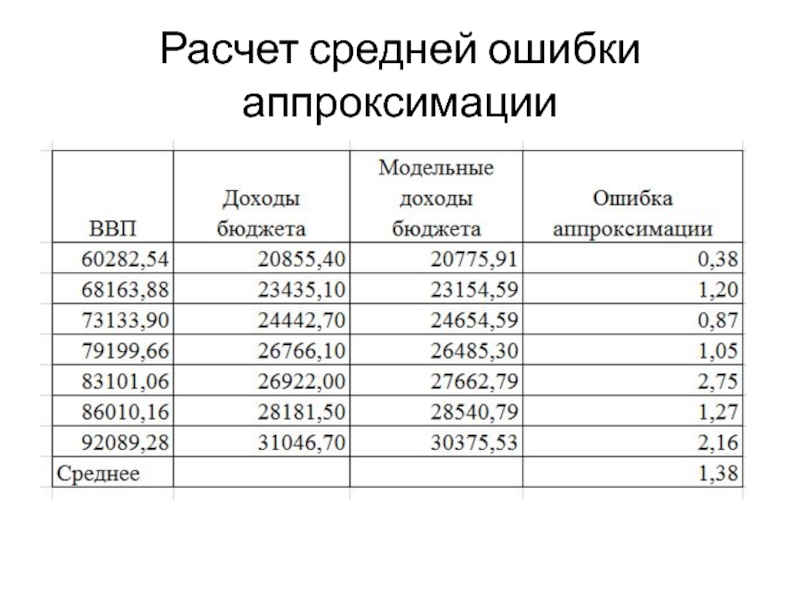
Слайд 10Средняя ошибка аппроксимации
Средняя ошибка аппроксимации – среднее относительное отклонение расчетных
значений от фактических.
Построенное уравнение регрессии считается удовлетворительным, если значение
не превышает 10 – 12 %. Слайд 17Интерпретация результатов
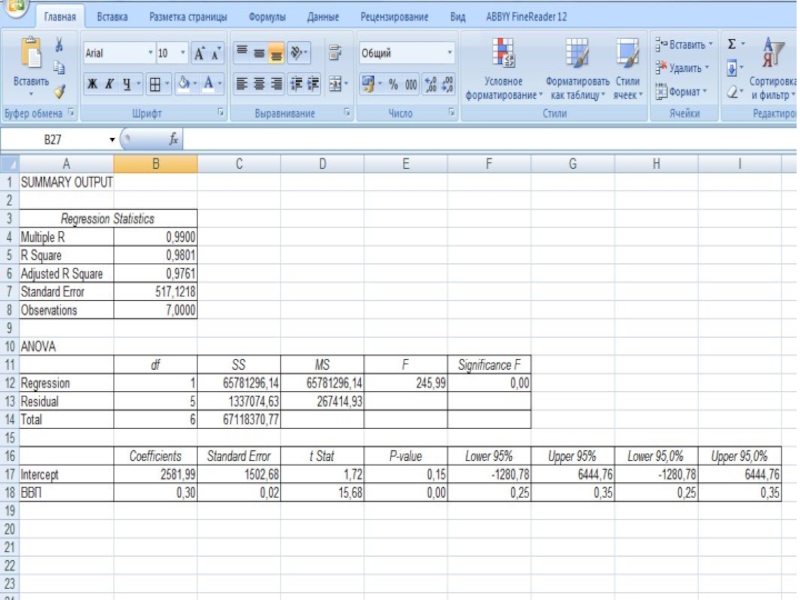
С увеличением ВВП на 1 млрд.руб. в среднем доходы
бюджета возрастают на 0,3 млрд.руб.
В данном случае величина коэффициента корреляции
является существенной, сила связи – весьма высокая, что позволяет сделать вывод о том, что ВВП – один из главных факторов, от которых зависит размер доходов бюджета.Доходы бюджета на 98% зависят от размера ВВП и на 2% - от прочих факторов, не включенных в модель.
Слайд 19Вывод о качестве модели
Построенное уравнение регрессии считается отличным, поскольку значение
средней ошибки аппроксимации не превышает 1,5%.
Высокое значение критерия Фишера свидетельствует
о достоверности полученного уравнения (связь доказана).Поскольку табличное значение критерия Стьюдента равно 2,45, фактическое значение критерия для коэффициента регрессии превышает табличное, гипотезу о несущественности коэффициента регрессии можно отклонить, коэффициент регрессии является значимым.
Параметр регрессии статистически не значим.