Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стереометрия
Содержание
- 1. Стереометрия
- 2. Стереометрия.Стереометрия — раздел геометрии, в котором изучаются свойства фигур
- 3. Многогранник.Многогранник представляет собой тело, поверхность которого состоит из
- 4. Многогранники
- 5. Многогранники. Призма.Призмой (n-угольной призмой) называется многогранник, две
- 6. Многогранники. Призма.Прямой призмой называется призма, боковое ребро
- 7. Соотношения для прямой призмы. H — высота
- 8. Особенности правильной шестиугольной призмы. Свойства.
- 9. Многогранник. Прямоугольный параллелепипед.Прямая призма, у которой основанием
- 10. Многогранник. Прямоугольный параллелепипед.– Противоположные грани прямоугольного параллелепипеда
- 11. Многогранник. Куб.Куб — правильный многогранник, каждая грань
- 12. Многогранник. Соотношения для куба.а — длина ребра
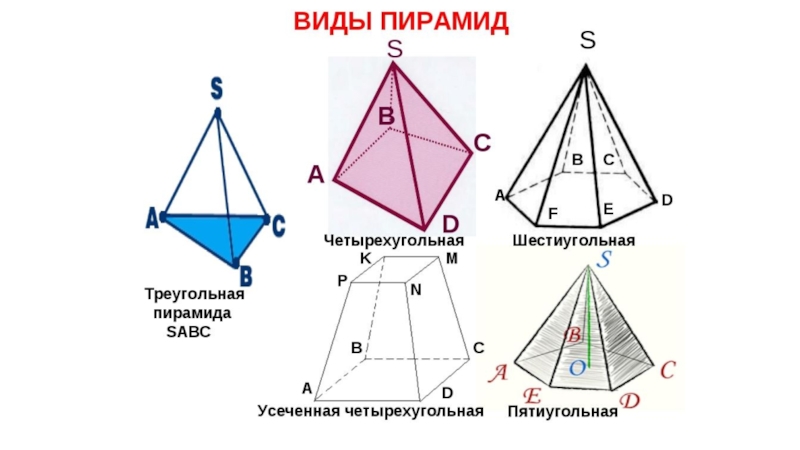
- 13. Многогранник. Пирамида. Пусть вне плоскости многоугольника A1,
- 14. Слайд 14
- 15. Соотношения для правильной пирамидыH — высота правильной
- 16. Слайд 16
- 17. Сечение многогранников.Секущей плоскостью многогранника называется любая плоскость,
- 18. Примеры сечения.Тетраэдр имеет четыре грани, поэтому его
- 19. Теорема 1. Если две параллельные плоскости пересечены
- 20. Алгоритм построения сечения1. Если две точки секущей
- 21. Круглые тела. ЦилиндрЦилиндр. Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.
- 22. Соотношения для цилиндра. h — высота цилиндра
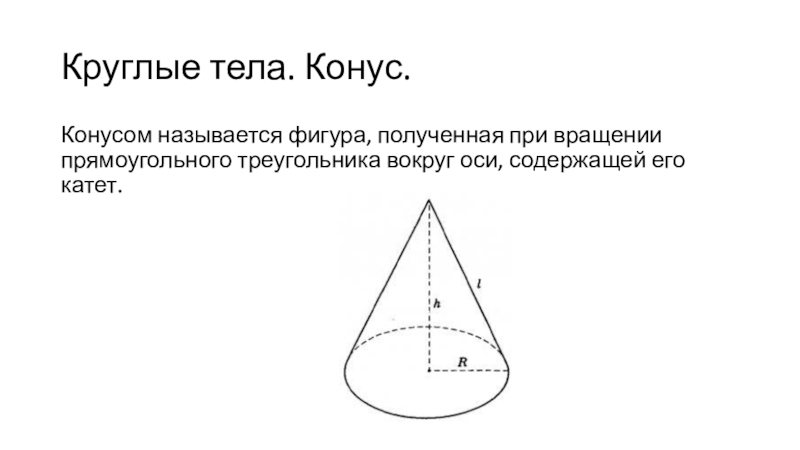
- 23. Круглые тела. Конус. Конусом называется фигура, полученная
- 24. Соотношения для конуса. h — высота конусаr
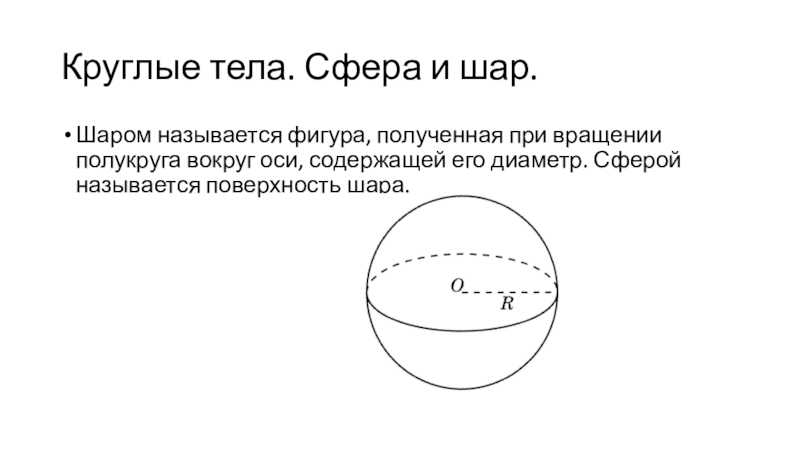
- 25. Круглые тела. Сфера и шар. Шаром называется
- 26. Соотношения для сферы и шара
- 27. Комбинации круглых тел. Вписанные сферы Сфера
- 28. Теорема 1. В прямой круговой цилиндр можно
- 29. Описанные сферы Сфера называется описанной около цилиндра,
- 30. Теорема 1: около цилиндра можно описать сферу
- 31. Комбинации конуса и цилиндра Цилиндр называется
- 32. КОМБИНАЦИИ МНОГОГРАННИКОВ И КРУГЛЫХ ТЕЛ. Описанные
- 33. Теорема 1: если из центра описанной около
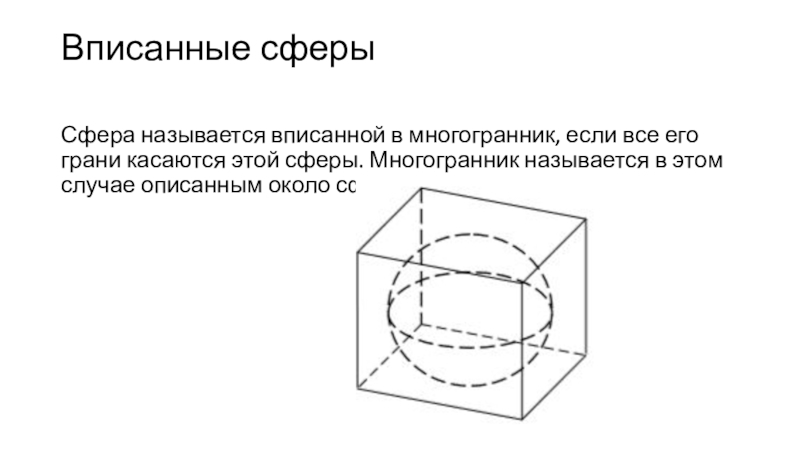
- 34. Вписанные сферы Сфера называется вписанной в
- 35. Скачать презентанцию
Стереометрия.Стереометрия — раздел геометрии, в котором изучаются свойства фигур в пространстве. Основными (простейшими) фигурами в пространстве являются точки, прямые и плоскости. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих
Слайды и текст этой презентации
Слайд 2Стереометрия.
Стереометрия — раздел геометрии, в котором изучаются свойства фигур в пространстве. Основными
Слайд 3Многогранник.
Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников.
Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников
называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми и невыпуклыми .Слайд 5Многогранники. Призма.
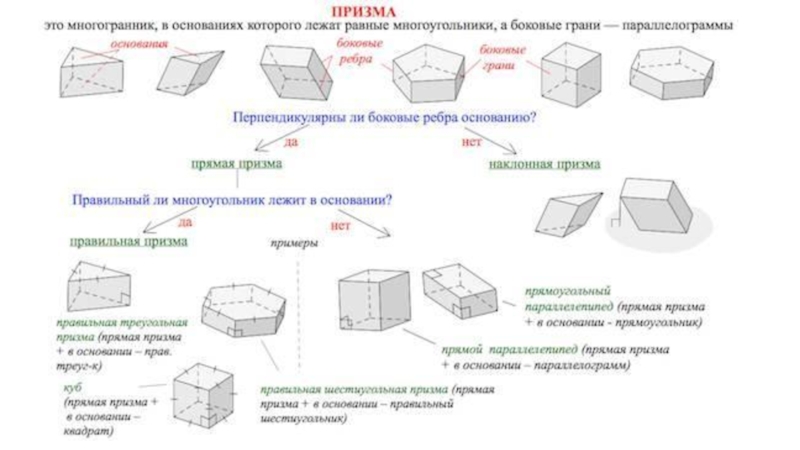
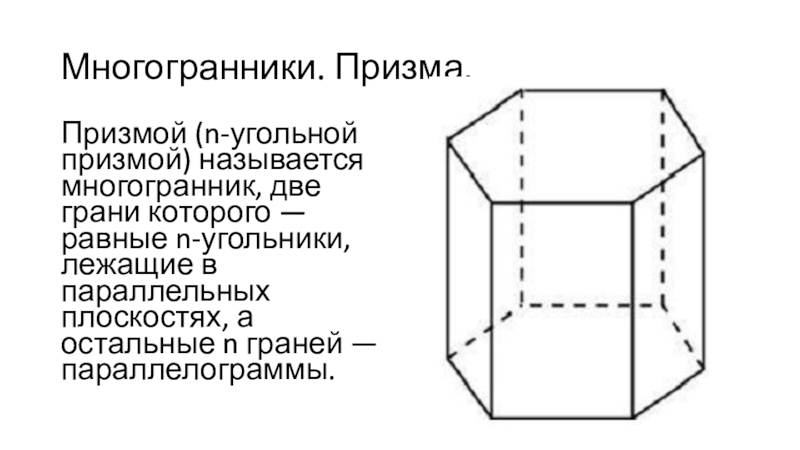
Призмой (n-угольной призмой) называется многогранник, две грани которого —
равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней
— параллелограммы.Слайд 6Многогранники. Призма.
Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости
основания. Высота прямой призмы равна ее боковому ребру, а все
боковые грани прямой призмы — прямоугольники. Правильной призмой называется прямая призма, основание которой — правильный многоугольник.Слайд 7Соотношения для прямой призмы.
H — высота прямой призмы
AA1
— боковое ребро
P осн — периметр основания
S осн —
площадь основанияS бок— площадь боковой поверхности
S полн — площадь полной поверхности
V — объем прямой призмы
S бок = Pосн * AA1
S полн = 2 * S осн + S бок
V = S осн * H
Слайд 9Многогранник. Прямоугольный параллелепипед.
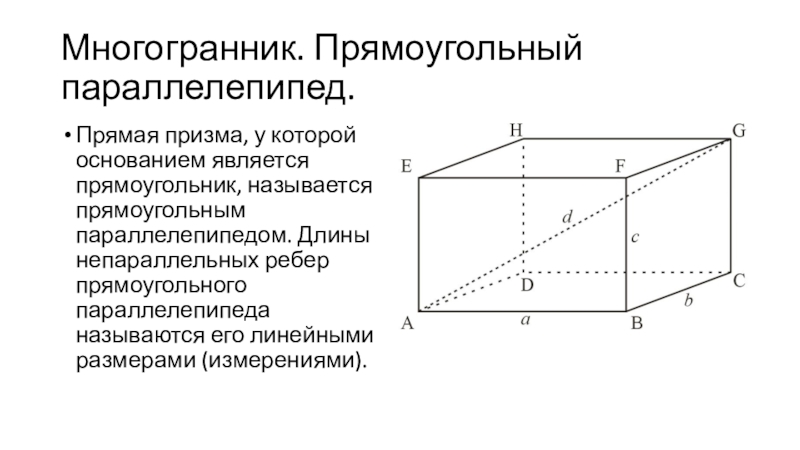
Прямая призма, у которой основанием является прямоугольник, называется
прямоугольным параллелепипедом. Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными
размерами (измерениями).Слайд 10Многогранник. Прямоугольный параллелепипед.
– Противоположные грани прямоугольного параллелепипеда — параллельные и
равные прямоугольники.
– Все четыре диагонали параллелепипеда пересекаются в одной
точке и делятся этой точкой пополам. – Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений: d 2 = a2 + b2+c2
– Площадь полной поверхности прямоугольного параллелепипеда равна удвоенной сумме попарных произведений его измерений:
S полн = 2(ab+bc+ac) .
– Объем прямоугольного параллелепипеда равен произведению его измерений : V = abc
Слайд 11Многогранник. Куб.
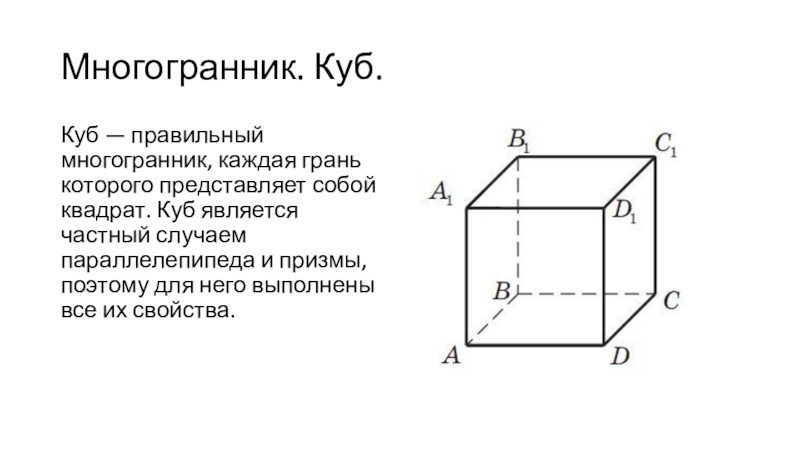
Куб — правильный многогранник, каждая грань которого представляет собой
квадрат. Куб является частный случаем параллелепипеда и призмы, поэтому для
него выполнены все их свойства.Слайд 12Многогранник. Соотношения для куба.
а — длина ребра куба
d осн —
диагональ основания
d — диагональ куба
S полн — площадь полной
поверхностиV — объем куба
Слайд 13Многогранник. Пирамида.
Пусть вне плоскости многоугольника A1, A2,…An задана точка
P. Тогда фигура, образованная треугольниками A1PA2 , A2 P A3
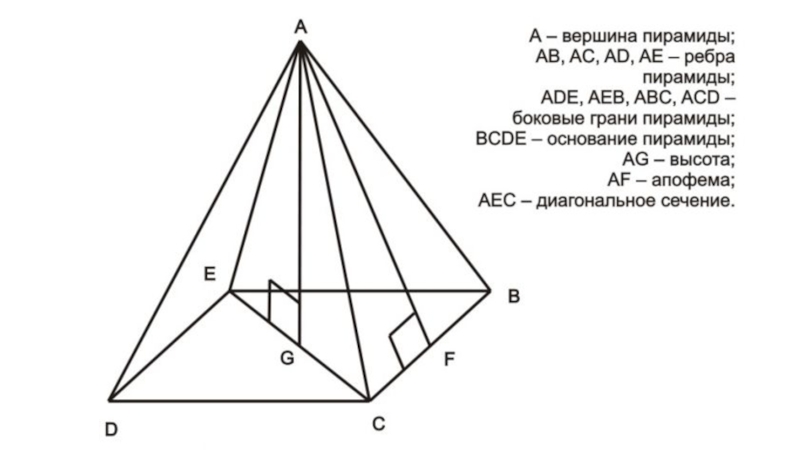
, …, An P A1 и многоугольником A1A2… An вместе с их внутренними областями называется пирамидой (n-угольной пирамидой). Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.Слайд 15Соотношения для правильной пирамиды
H — высота правильной пирамиды
h —
ее апофема
P осн — периметр основания пирамиды
S осн — площадь
основания S бок — площадь боковой поверхности
S полн— площадь полной поверхности
V — объем правильной пирамиды.
Слайд 17Сечение многогранников.
Секущей плоскостью многогранника называется любая плоскость, по обе стороны
от которой имеются точки данного многогранника. Секущая плоскость пересекает грани
многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.Слайд 18Примеры сечения.
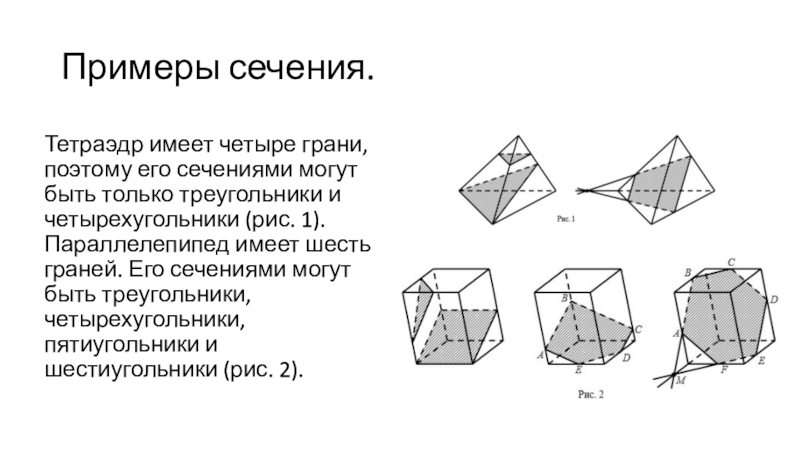
Тетраэдр имеет четыре грани, поэтому его сечениями могут быть
только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней.
Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).Слайд 19Теорема 1. Если две параллельные плоскости пересечены третьей, то линии
их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней
по параллельным прямым.Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости α, то она параллельна и самой плоскости α.
Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.
Слайд 20Алгоритм построения сечения
1. Если две точки секущей плоскости лежат в
плоскости одной грани, то проводим через них прямую. Часть прямой,
лежащая в плоскости грани — сторона сечения.2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.
3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.
Слайд 21Круглые тела. Цилиндр
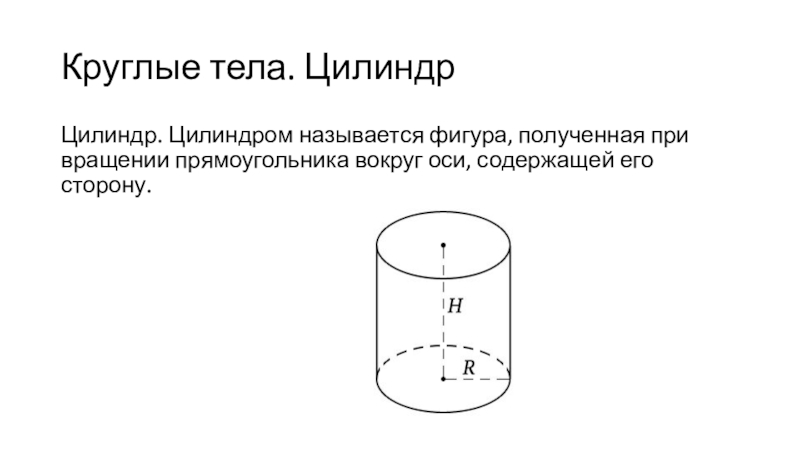
Цилиндр. Цилиндром называется фигура, полученная при вращении прямоугольника
вокруг оси, содержащей его сторону.
Слайд 22Соотношения для цилиндра.
h — высота цилиндра
r — радиус
основания
S бок — площадь боковой поверхности
S полн — площадь полной
поверхностиV — объем цилиндра
S бок = 2Пrh
S полн= 2Пr2+2Пrh
V = S осн h=Пr2h
Слайд 23Круглые тела. Конус.
Конусом называется фигура, полученная при вращении прямоугольного
треугольника вокруг оси, содержащей его катет.
Слайд 24Соотношения для конуса.
h — высота конуса
r — радиус основания
l
— образующая
S бок— площадь боковой поверхности
S полн— площадь
полной поверхностиV — объем конуса
Слайд 25Круглые тела. Сфера и шар.
Шаром называется фигура, полученная при
вращении полукруга вокруг оси, содержащей его диаметр. Сферой называется поверхность
шара.Слайд 27Комбинации круглых тел. Вписанные сферы
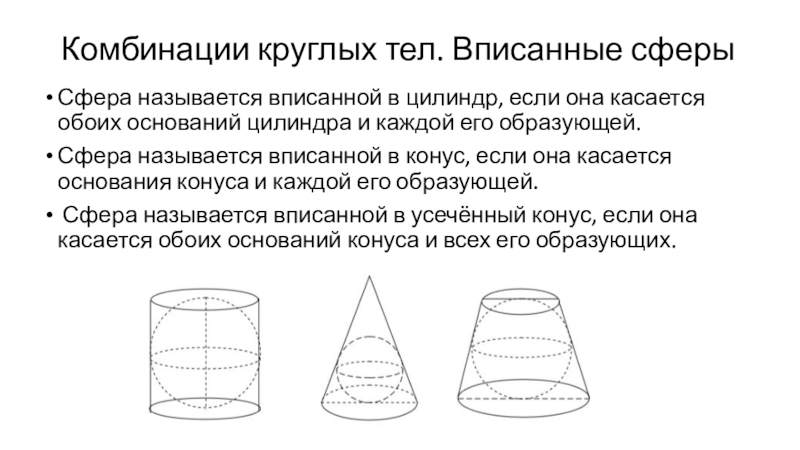
Сфера называется вписанной в цилиндр,
если она касается обоих оснований цилиндра и каждой его образующей.
Сфера называется вписанной в конус, если она касается основания конуса и каждой его образующей.
Сфера называется вписанной в усечённый конус, если она касается обоих оснований конуса и всех его образующих.
Слайд 28Теорема 1. В прямой круговой цилиндр можно вписать сферу тогда
и только тогда, когда его высота равна диаметру основания. Причём
центр сферы есть середина оси цилиндра.Теорема 2: в любой прямой круговой конус можно вписать сферу. Причём центр сферы есть точка пересечения оси конуса с биссектрисой угла наклона образующей конуса к плоскости его основания.
Теорема 3. в усечённый конус можно вписать сферу тогда и только тогда, когда он прямой круговой, и длина его образующей равна сумме длин радиусов оснований. Причём центр сферы есть середина оси усечённого конуса.
Слайд 29Описанные сферы
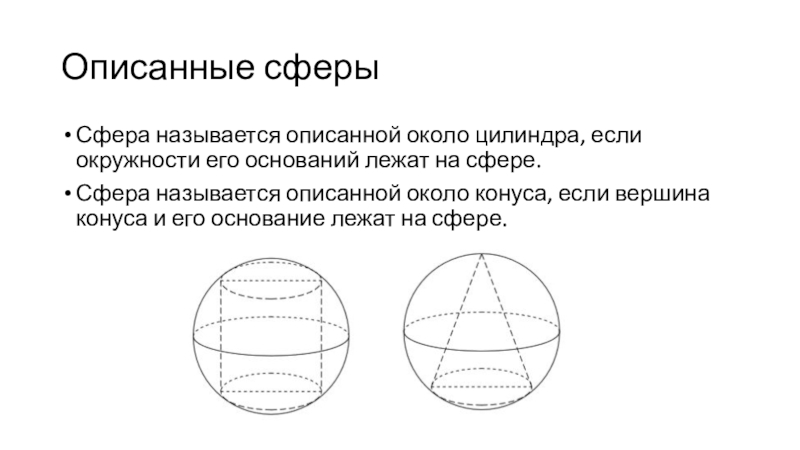
Сфера называется описанной около цилиндра, если окружности его
оснований лежат на сфере.
Сфера называется описанной около конуса, если
вершина конуса и его основание лежат на сфере.Слайд 30Теорема 1: около цилиндра можно описать сферу тогда и только
тогда, когда он прямой круговой. Причём центр сферы есть середина
оси цилиндра.Теорема 2: около конуса можно описать сферу тогда и только тогда, когда он круговой. Причём центр сферы есть точка пересечения прямой, перпендикулярной к плоскости основания и проходящей через центр его, и плоскости, перпендикулярной какой-либо его образующей конуса и проходящей середину этой образующей.
Следствие: сферу можно описать около любого прямого кругового конуса. В этом случае, центр сферы — точка пересечения прямой, содержащей высоту конуса с плоскостью, перпендикулярной какой-либо из его образующих и проходящей через ее середину.
Слайд 31Комбинации конуса и цилиндра
Цилиндр называется вписанным в конус, если
одно его основание лежит на основании конуса, а второе совпадает
с сечением конуса плоскостью, параллельной основанию. Конус в этом случае называется описанным вокруг цилиндра.Цилиндр называется описанным вокруг конуса, если центр одного из оснований цилиндра является вершиной вершина конуса, а противоположное основание цилиндра совпадает с основанием конуса. Конус в этом случае называется вписанным в цилиндр.
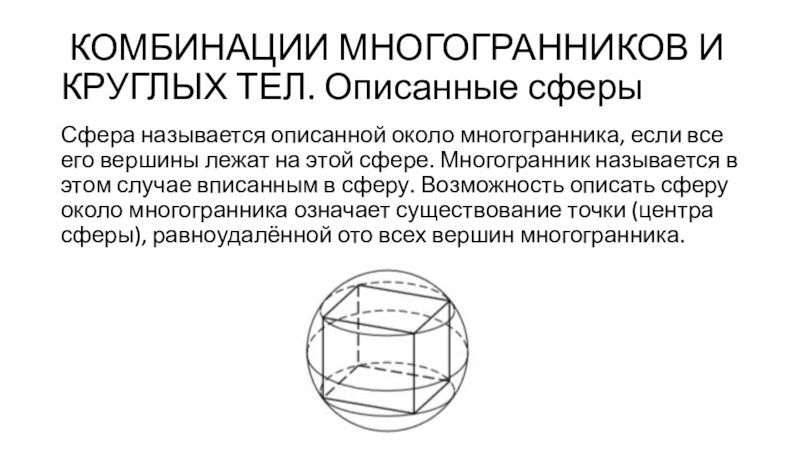
Слайд 32 КОМБИНАЦИИ МНОГОГРАННИКОВ И КРУГЛЫХ ТЕЛ. Описанные сферы
Сфера называется
описанной около многогранника, если все его вершины лежат на этой
сфере. Многогранник называется в этом случае вписанным в сферу. Возможность описать сферу около многогранника означает существование точки (центра сферы), равноудалённой ото всех вершин многогранника.Слайд 33Теорема 1: если из центра описанной около многогранника сферы опустить
перпендикуляр на какое-либо из его рёбер, то основание этого перпендикуляра
разделит ребро на две равные части.Теорема 2: если из центра описанной около многогранника сферы опустить перпендикуляр на какую-либо из его граней, то основание этого перпендикуляра попадёт в центр круга, описанного около соответствующей грани.
Теорема 3: если около многогранника описана сфера, то её центр лежит на пересечении перпендикуляров к каждой грани пирамиды, проведённых через центр окружности, описанной около соответствующей грани.
Теорема 4: если около многогранника описана сфера, то её центр является точкой пересечений всех плоскостей, проведённых через середины рёбер пирамиды перпендикулярно к этим рёбрам.