СУЭП переменного тока

с управляемым регулятором напряжения:
СУ асинхронным электроприводом с импульсным регулятором в

напряжения

составляющая

где

а свободная составляющая тока





из условия, что
в момент

Окончательно

0 или U = 0 при α+λ-π < ω⋅t < α

Угол проводимости λ зависит от α и ϕ

Подставляя ωt = α + ϕ

sin(α+λ-ϕ) - sin(α -ϕ)⋅ eхр-λ/tg = 0.

Характеристики ТРН рассматриваются, в виде семейства характеристик
Uтрн = f(α,ϕ)

Обычно выходное напряжение ТРН представляют только его первой
гармоникой

Для управляемого электропривода целесообразно построить семейство
характеристик управления U1* = U1/Uном = f(α) при фиксированных
значениях угла нагрузки ϕ = const

импульсов
Основные узлы СИФУ: аналогово-цифровой преобразователь, генератор,
счетчик, дешифратор и

и дифференцирующей цепи C2R15.
Генератор выполнен на элементе D6, счётчик

По переднему фронту каждого синхроимпульса "Синх." дифференцирующей цепочкой С7R5 вырабатывается импульс, по которому элементы D1.3, D1.4 кратковременно открываются, и происходит разряд конденсатора интегрирующей цепи C1R13. По окончании этого импульса через R13 начинается заряд конденсатора С1

Потенциал на инверсном входе усилителя А2 является опорным сигналом
и соответствует величине напряжения сигнала управления, поступающего
на вход СИФУ

Когда потенциал пилообразного напряжения на конденсаторе С1 начнёт
превышать потенциал входа 4 этого усилителя, на выходе компаратора
появляется сигнал положительной полярности, а с выхода
дифференцирующей цепи C2R15 выдаётся кратковременный импульс
единичного уровня, по которому счётчик D5 сбрасывается в нулевое
состояние

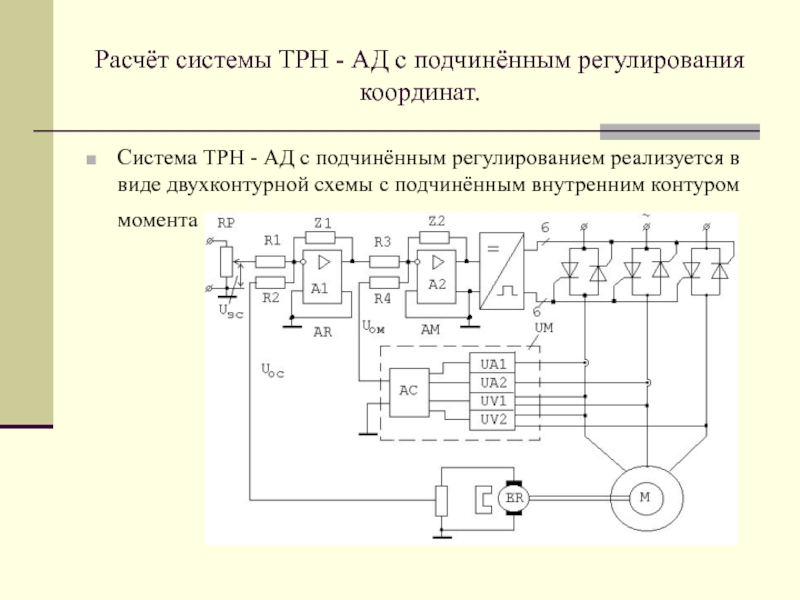
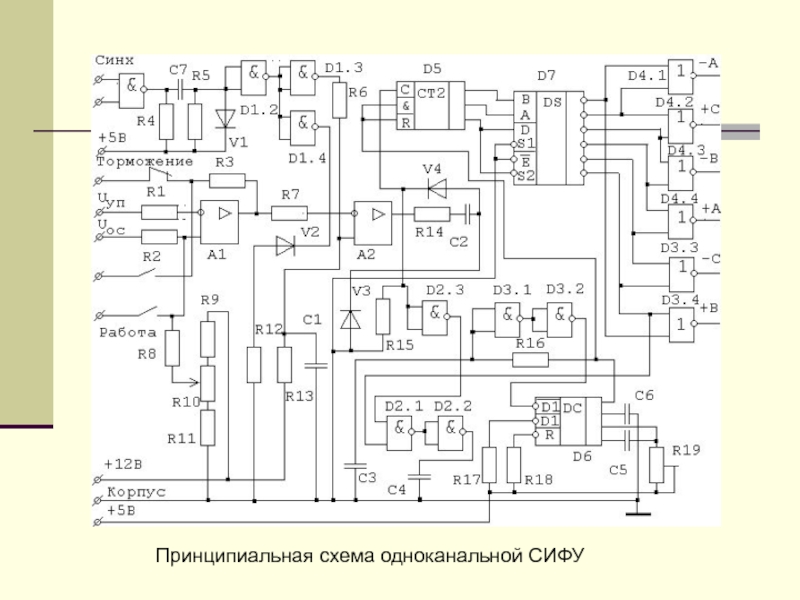
дешифратора D7 устанавливается единичный уровень. Этот сигнал
подаётся на вход

Эти импульсы подсчитываются счётчиком D5, по выходной информации
которого на соответствующем выходе дешифратора D7 появляется сигнал
нулевого уровня

Когда генератор выработает пять импульсов, сигналом с шестого выхода
дешифратора, он затормаживается. По переднему фронту очередного
синхроимпульса счётчик D5 сбрасывается в нулевое состояние, на выходе
6 элемента D7 устанавливается сигнал единичного уровня, и генератор
начинает выработку очередной серии импульсов. Длительность импульсов
определяется цепочкой C3R16, а период - цепочкой С6R19.

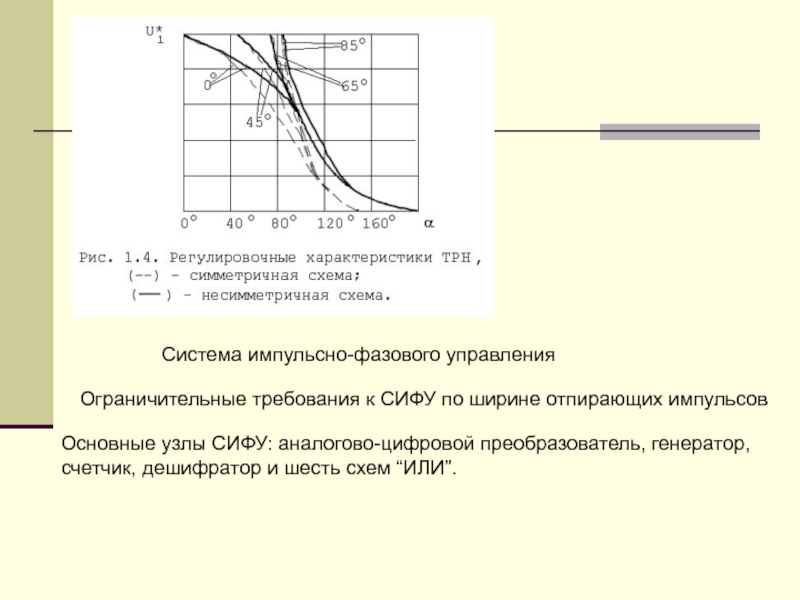
Каждому уровню сигнала управления соответствует определённое значение
напряжения на выходе усилителя А1, а следовательно, и фаза выходного
сигнала компаратора А2

замещения двигателя (см.рис.), можно связать основные координаты электропривода с параметрами

Характеристики двигателя при фазовом управлении разомкнутой ТРН-АД

системе можно пояснить рисунком:
Анализ статических характеристик замкнутой системы
Uу =

где KR = Rвх /(R1+ R3+ R4'+ Rвх);

Uос = Кс ω.

Или

Первое уравнение запишется в виде
Uу = [Uз−Kс⋅ω − KR⋅KТ⋅(I1− I1отс)]

Uуп = KА1⋅Uу ,

Далее записывая

α - αmax = Kф Uуп,

Путем подстановки получим

α = αmax − Kф⋅KА1⋅[Uз − Kс⋅ω - KR⋅KТ⋅ (I1− I1отс)].

Если (I1 < I1ОТС)

этом случае при анализе удобно использовать зависимость U1*2 = f(Uуп,ϕ)

Для конкретного двигателя определив значение угла ϕ = arctg(ωLд/Rд),
и выбрав для этого угла кривую U1*2 = f(Uуп, ϕ), при линеаризации её
получим

U1*2 = Kп' Uуп,

Если (I1 < I1ОТС)

заданному
статизму и диапазону регулирования скорости:


Необходимое значение коэффициента усиления

Необходимое значение KА1 можно определить и графоаналитически

учитывая, что заданная погрешность стабилизации скорости ΔωТР = ωа− ωг,

I1отс)] = αmax − αдоп
получаем:

- АД с подчинённым регулированием реализуется в виде двухконтурной схемы

γ1 ~σ /2 и γ2 ~2SK
а для серийных АД

значения коэффициентов затухания

γ1~(0,005...0,025),

γ2 ~ (0,4...1,0).

Тогда в выражении (1 + γ1⋅γ2)/(γ2 − γ1) ≅ 1/γ2, а ехр -γ1⋅Ω0⋅t >> ехр-γ2⋅Ω0⋅t.

Обозначим 1/γ1⋅Ω0 = T1, 1/γ2⋅Ω0 = Т2

Т1 = (0,1...0,6)c; T2 = (0,003...0,008)c

Пренебрегая в уравнении малыми величинами получим:

тремя составляющими: установившейся
(Муст = Мп); апериодической (Ма = Мп⋅

Тогда передаточная функция АД будет выглядеть:

Учитывая малое демпфирование колебаний (γ1 << 1), последнее
выражение можно упростить:

Структурная схема двухконтурной системы регулирования скорости с учётом
линеаризации характеристик АД и ТРН будет иметь вид

малую постоянную времени внутреннего контура примем Тμ=Т2+ τп,
При расчете

ПФ разомкнутого внутреннего контура регулирования

1/(2TμKмKпKомр). Такая разбивка обусловлена тем, что звено с ПФ Т02р2+1

передаточная функция регулятора момента

Тф=Т0/(2-3)

Tμ= Т2+τп+2⋅ξ⋅Tф