Региональная экономика

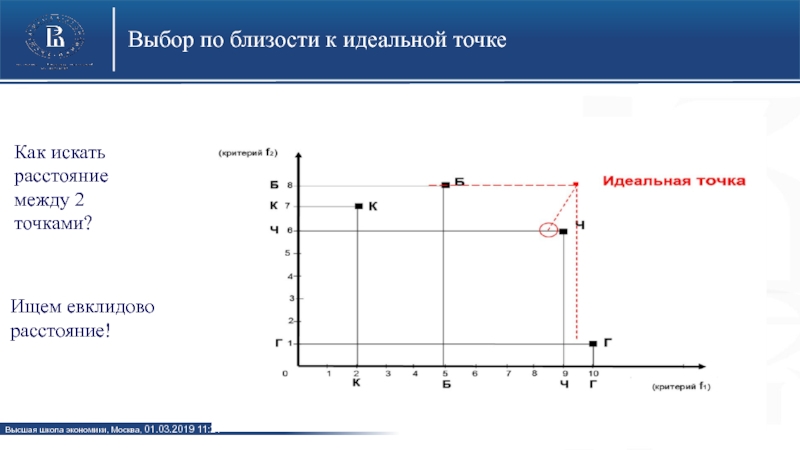
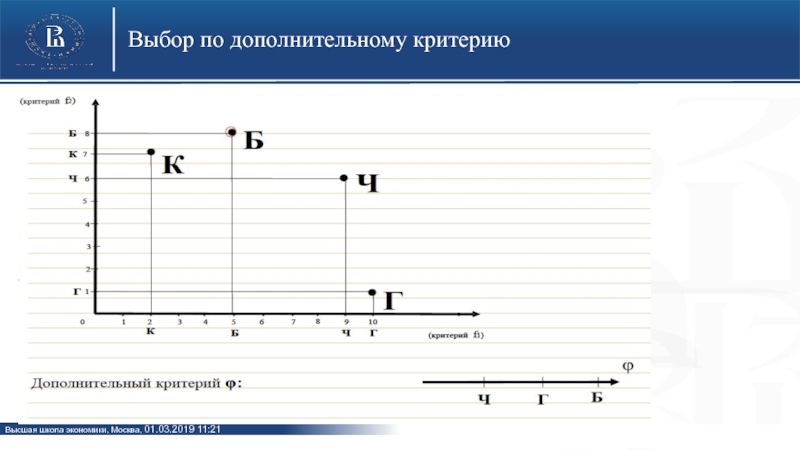
не так просто.
Большинство может быть разным:
Простым (50%+1 голос от общего

числа участвовавших в голосовании избирателей)
Абсолютным (50% + 1 голос от общего числа избирателей)
Относительным (когда проголосовало больше, чем за соперника)
Квалифицированным (например, 2/3 – конституционное большинство в Российской Федерации)

избирателю проранжировать для себя каждого из кандидатов

Считаем голоса кандидатов, которых

избиратели поставили первыми. Если никто не набрал простого большинства, то:
Лузер первого тура «ликвидируется» из голосования
Смотрим, кто в бюллютенях этого «лузера» шел вторым
Суммируем голоса за этого «второго» с уже имеющимися результатами.

Повторяем до тех пор, пока не наберется абсолютное (иногда – простое) большинство.


Другое название метода – преференциальное голосование.

Самый признанный «практик» в части использования данного метода – Австралия (с 1918 г.)

искать «самого слабого» кандидата каждый раз, просто считаем, что:
Первое предпочтение

– 1 балл
Второе предпочтение – ½ балла
Третье предпочтение – 1/3 балла
…
…
n-ое предпочтение - 1/n балла.

Считаем баллы каждого кандидата.

Определяем победителя.

или иные решения. В следующий раз – как их можно

оценить.

Для государственного и муниципального управления важны оба данных процесса (самое простое и практичное понимание политического действия (процесса) – попытка договориться, какое общественное благо мы будем производить)

Методы могут использоваться не только при решении вопросов государственного значения, но и при решении личных вопросов. Но отличия, конечно же, есть (поговорим об этом в следующий раз, когда будем говорить об оценке альтернатив)

Как правило, методы выбора достаточно просты

называем «паретовскими» будут составлять Парето-множество.

Множество альтернатив, которое попарно не

доминируется друг другом, называется множеством Парето, в честь великого ученого XIX в. Вильфредо Парето.

Ограничение?
(больше 2 критериев – сложно визуально определить)

вариантов, сколько необходимо включить в выбранное множество по условию данной

конкретной задачи (все нормально)

В множество Парето входит больше вариантов, чем требуется выбрать по условиям данной конкретной задачи (кого убирать?)

В множество Парето входит меньше вариантов, чем требуется выбрать по условиям данной конкретной задачи (где искать?)

– используем альтернативные методы оценки.

Если третья – обрезаем множество. Вернемся

к первоначальной картинке:

Как вариант (вместо слоев) – надпороговые значения.

баллов. Дать в баллах оценку каждому из критериев
Сложить полученные баллы.

Произвести нормировку весов критериев, разделив присвоенные баллы на сумму весов
Измерить значение каждой альтернативы по каждому из критериев по шкале от 0 до 100 баллов.
Определить общую оценку каждой альтернативы, используя формулу взвешенной суммы баллов (см. предыдущий слайд)
Выбрать как лучшую альтернативу, имеющую наибольшую общую оценку
Произвести оценку чувствительности результата к изменениям весов

критериям.
Никаких весов.

2 точками?
Ищем евклидово расстояние!

к единой шкале для удобства восприятия!

Как определить лучшую альтернативу?

Сравнить площади

каждой альтернативы
Найти отношение площади каждой альтернативы к идеальной ситуации и сравнить