TheSlide.ru

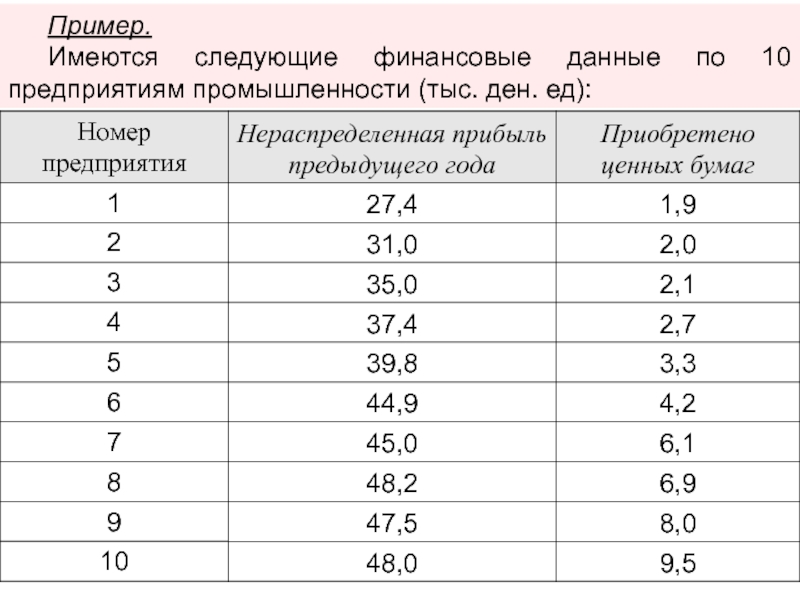
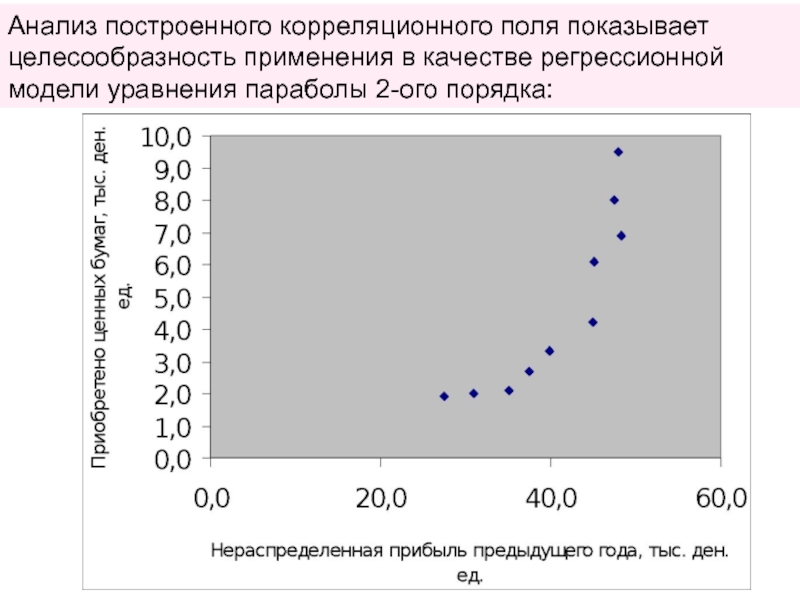
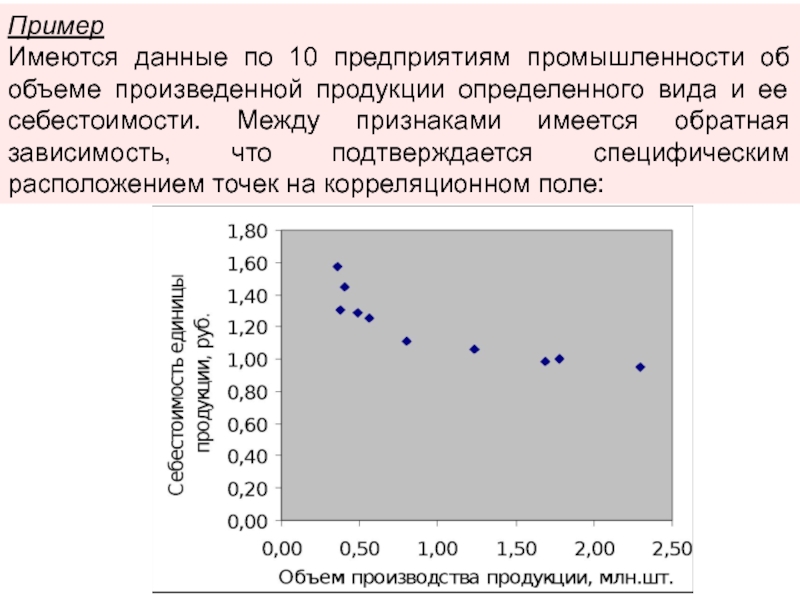
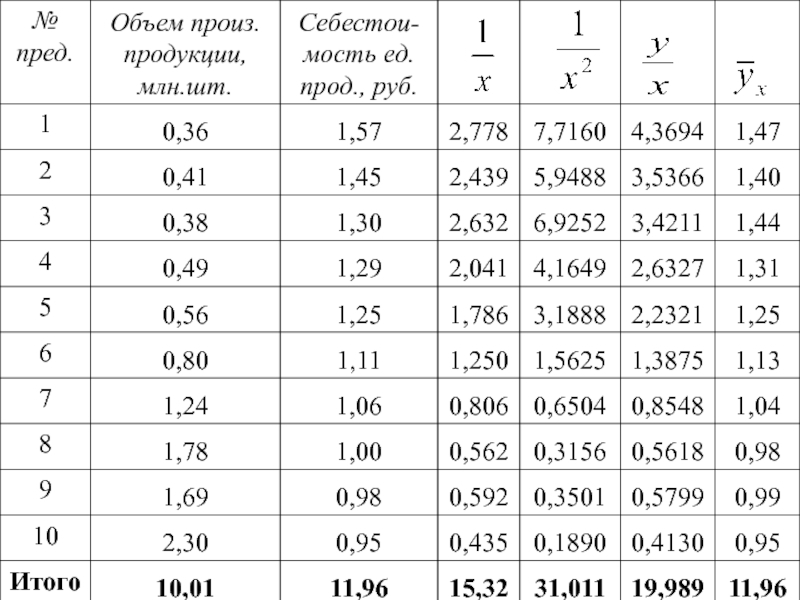
Связь явлений Часть 1

Содержание

1. Связь явлений Часть 1
2. Пример. Имеются следующие финансовые данные по 10 предприятиям промышленности (тыс. ден. ед):
3. Анализ построенного корреляционного поля показывает целесообразность применения в качестве регрессионной модели уравнения параболы 2-ого порядка:
4. Слайд 4
5. Составим систему нормальных уравнений:Решив ее, получаем значения
6. Насколько «хорошо» данное уравнение описывает взаимосвязь признаков
7. Гиперболическое уравнение парной регрессииГиперболическая зависимость имеет место,
8. Для оценки параметров гиперболы в случае парной зависимости используется следующая система нормальных уравнений:
9. ПримерИмеются данные по 10 предприятиям промышленности об
10. Слайд 10
11. а0 = 0,857512 и а1 = 0,220945.
12. Скачать презентанцию

Пример. Имеются следующие финансовые данные по 10 предприятиям промышленности (тыс. ден. ед):

Слайды и текст этой презентации

Слайд 1Параболическое уравнение парной регрессии

Равноускоренное изменение результативного признака у при равномерном

изменении фактора х говорит о параболической связи между признаками.
При

этом в некоторой точке связь может поменять свое направление: прямая связь перейти в обратную и наоборот.
При парной параболической зависимости уравнение регрессии имеет вид:

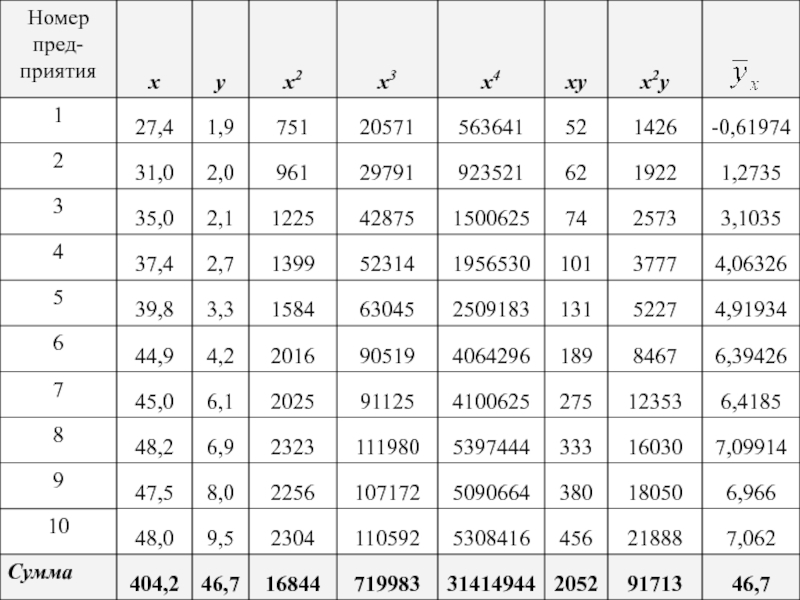
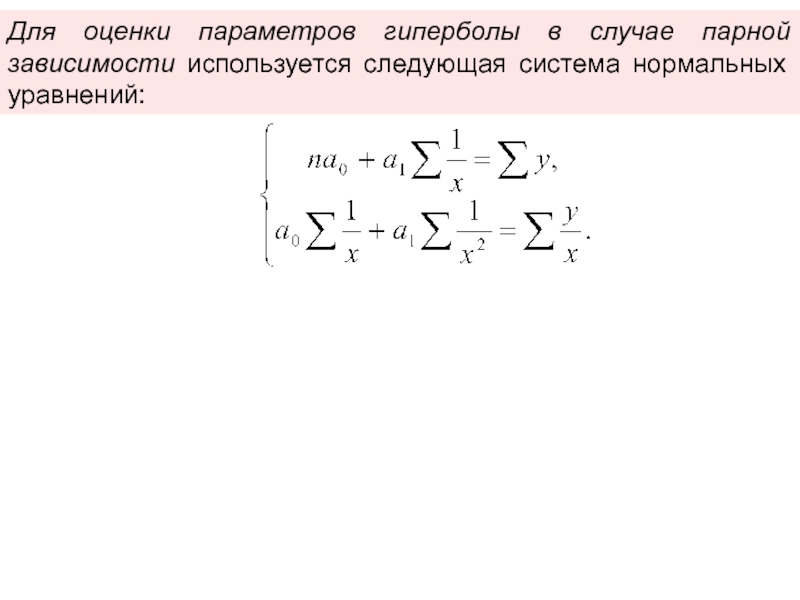
Параметры уравнения находят из следующей системы нормальных уравнений:

Параболическое уравнение парной регрессииРавноускоренное изменение результативного признака у при равномерном изменении фактора х говорит о параболической связи

Слайд 2Пример.
Имеются следующие финансовые данные по 10 предприятиям промышленности (тыс.

ден. ед):

Пример. Имеются следующие финансовые данные по 10 предприятиям промышленности (тыс. ден. ед):

Слайд 3Анализ построенного корреляционного поля показывает целесообразность применения в качестве регрессионной

модели уравнения параболы 2-ого порядка:

Анализ построенного корреляционного поля показывает целесообразность применения в качестве регрессионной модели уравнения параболы 2-ого порядка:

Слайд 4

Слайд 5Составим систему нормальных уравнений:

Решив ее, получаем значения для оценок параметров

регрессии:
а0 = -22,674; а1 = 1,052; а2 = -0,009.
Искомое уравнение

параболы имеет вид:

Подставляя в полученное уравнение значения факторной
переменной х, рассчитаем выравненные значения

Составим систему нормальных уравнений:Решив ее, получаем значения для оценок параметров регрессии:а0 = -22,674; а1 = 1,052; а2

Слайд 6Насколько «хорошо» данное уравнение описывает взаимосвязь признаков можно судить, рассчитав

теоретическое корреляционное отношение:

Как видим, связь между признаками сильная.
Теоретический коэффициент детерминации,

соответственно равный

говорит о том, что построенное параболическое уравнение
описывает вариацию зависимой переменной на 94,9 %.

Насколько «хорошо» данное уравнение описывает взаимосвязь признаков можно судить, рассчитав теоретическое корреляционное отношение:Как видим, связь между признаками

Слайд 7Гиперболическое уравнение парной регрессии

Гиперболическая зависимость имеет место, если связь между

признаками обратная.
Обратная связь также может описываться линейным уравнением с

отрицательным значением коэффициента регрессии. По расположению точек на корреляционном поле можно выбрать окончательный вид уравнения.
При выборе гиперболы факторный признак не может принимать нулевое значение.

Уравнение гиперболы при парной зависимости между признаками имеет вид:

Гиперболическое уравнение парной регрессииГиперболическая зависимость имеет место, если связь между признаками обратная. Обратная связь также может описываться

Слайд 8Для оценки параметров гиперболы в случае парной зависимости используется следующая

система нормальных уравнений:

Для оценки параметров гиперболы в случае парной зависимости используется следующая система нормальных уравнений:

Слайд 9Пример
Имеются данные по 10 предприятиям промышленности об объеме произведенной продукции

определенного вида и ее себестоимости. Между признаками имеется обратная зависимость,

что подтверждается специфическим расположением точек на корреляционном поле:

ПримерИмеются данные по 10 предприятиям промышленности об объеме произведенной продукции определенного вида и ее себестоимости. Между признаками

Слайд 10

Слайд 11а0 = 0,857512 и а1 = 0,220945.
Таким образом, искомое

уравнение гиперболы имеет вид:
.

Теоретический коэффициент детерминации равен:
Полученное уравнение

описывает вариацию зависимой переменной на 91,89 %.

а0 = 0,857512 и а1 = 0,220945. Таким образом, искомое уравнение гиперболы имеет вид: . Теоретический коэффициент

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей