Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тела вращения
Содержание
- 1. Тела вращения
- 2. Представляю вашему вниманию три тела вращения: конус,цилиндр и шар.
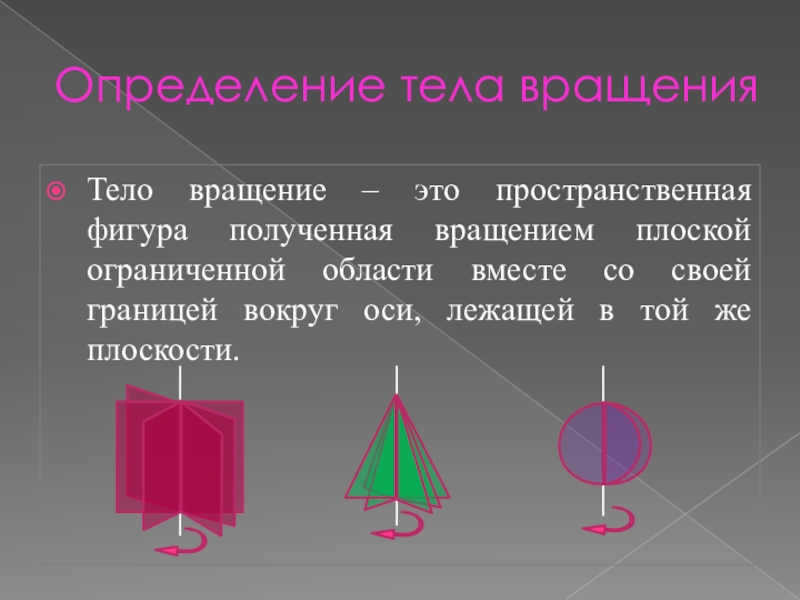
- 3. Определение тела вращенияТело вращение – это пространственная
- 4. ЦилиндрЦилиндр – это тело, которое описывает прямоугольник
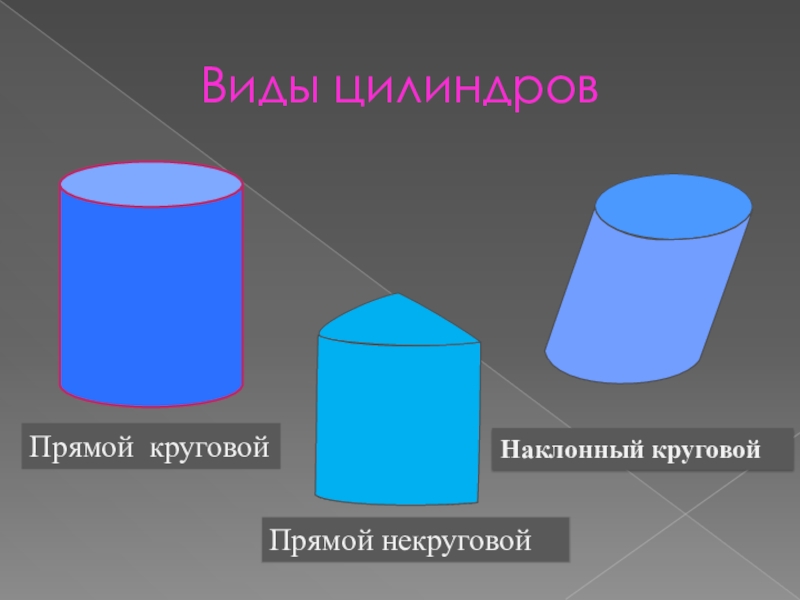
- 5. Виды цилиндровНаклонный круговойПрямой некруговойПрямой круговой
- 6. Сечения цилиндраОсевое сечение: Плоскость сечения содержит
- 7. Площадь поверхности цилиндра R Для вывода формулы
- 8. Цилиндр в нашей жизни
- 9. КонусКонус (круговой конус) – тело, которое состоит
- 10. КонусКонус – это тело, которое описывает прямоугольный
- 11. Сечение конуса Сечение плоскостью, параллельной основанию конуса:
- 12. Площадь поверхности конусаДля вывода формулы площади полной
- 13. Конус в нашей жизни
- 14. ШарШаром называется тело, которое состоит из всех
- 15. Сечения шараСечение шара, проходящее через его центр:В
- 16. Шар в нашей жизни
- 17. Задача на цилиндрРешение.1) Если дно шляпы опустить
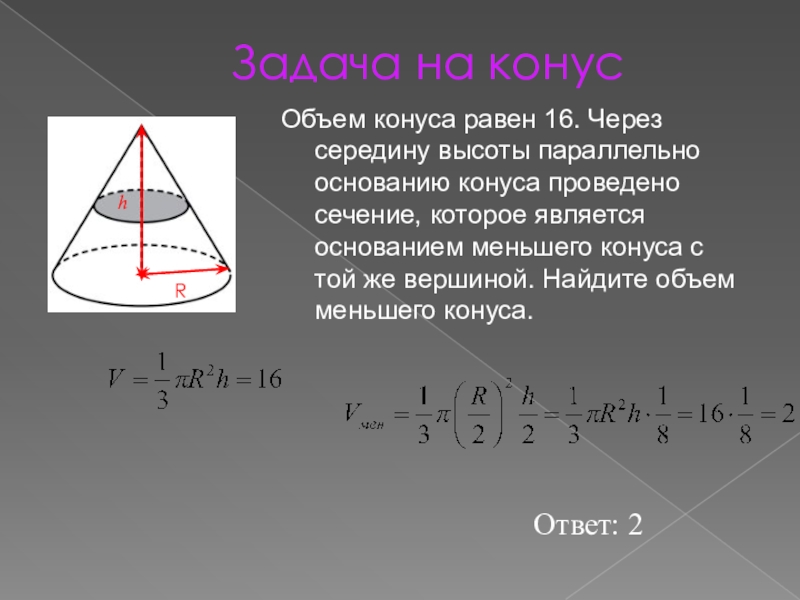
- 18. Задача на конусОбъем конуса равен 16.
- 19. Задач на шар Найдите длину полярного круга
- 20. Скачать презентанцию
Слайды и текст этой презентации
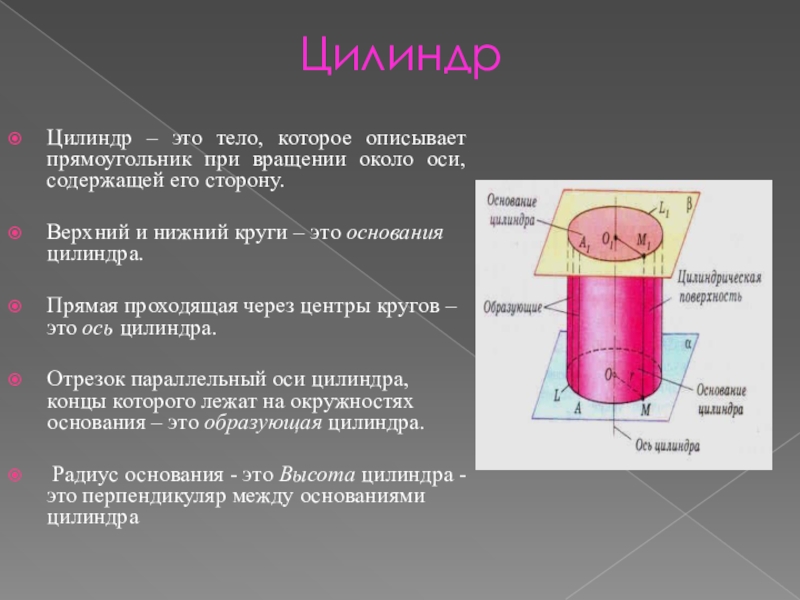
Слайд 4Цилиндр
Цилиндр – это тело, которое описывает прямоугольник при вращении около
оси, содержащей его сторону.
Верхний и нижний круги – это основания
цилиндра.Прямая проходящая через центры кругов – это ось цилиндра.
Отрезок параллельный оси цилиндра, концы которого лежат на окружностях основания – это образующая цилиндра.
Радиус основания - это Высота цилиндра - это перпендикуляр между основаниями цилиндра
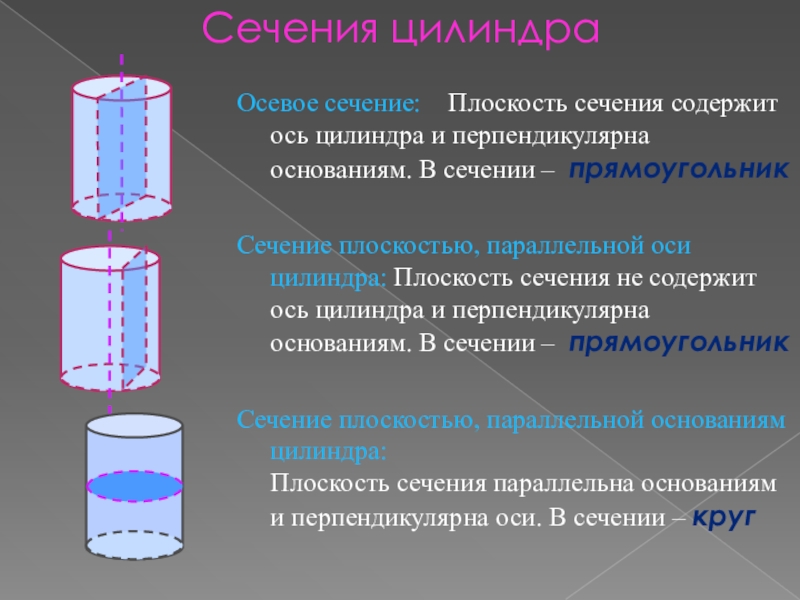
Слайд 6Сечения цилиндра
Осевое сечение: Плоскость сечения содержит ось цилиндра и
перпендикулярна основаниям. В сечении – прямоугольник
Сечение плоскостью, параллельной оси цилиндра:
Плоскость сечения не содержит ось цилиндра и перпендикулярна основаниям. В сечении – прямоугольникСечение плоскостью, параллельной основаниям цилиндра: Плоскость сечения параллельна основаниям и перпендикулярна оси. В сечении – круг
Слайд 7Площадь поверхности цилиндра
R
Для вывода формулы площади полной поверхности
цилиндра потребуется развертка цилиндра.
Полная поверхность состоит из 2 оснований
и боковой поверхности.Площадь основания находим как площадь круга:
S = R2
R – радиус основания цилиндра.
Боковая поверхность цилиндра есть прямоугольник.
Одна сторона прямоугольника
-это высота цилиндра(h), другая – длина окружности основания (2R)
Площадь боковой поверхности цилиндра равна произведению сторон прямоугольника: 2Rh
2 R
h
Слайд 9Конус
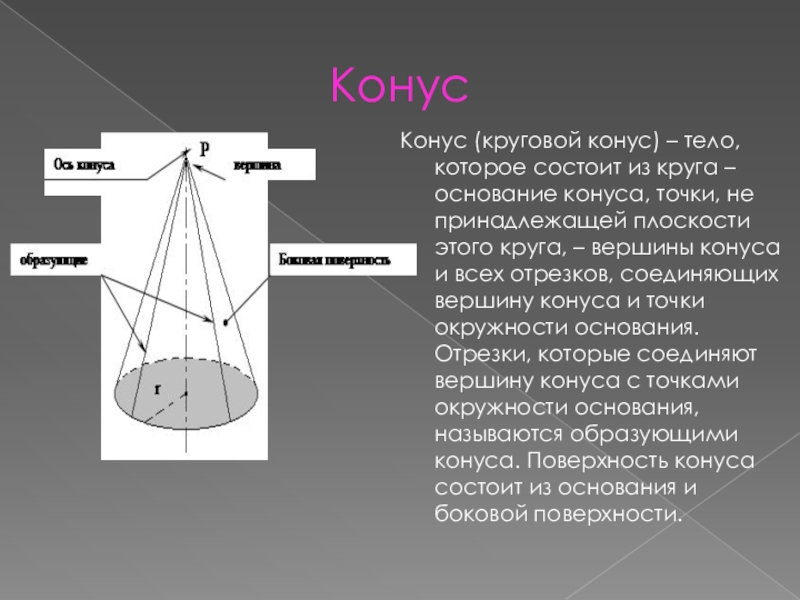
Конус (круговой конус) – тело, которое состоит из круга –
основание конуса, точки, не принадлежащей плоскости этого круга, – вершины
конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.Слайд 10Конус
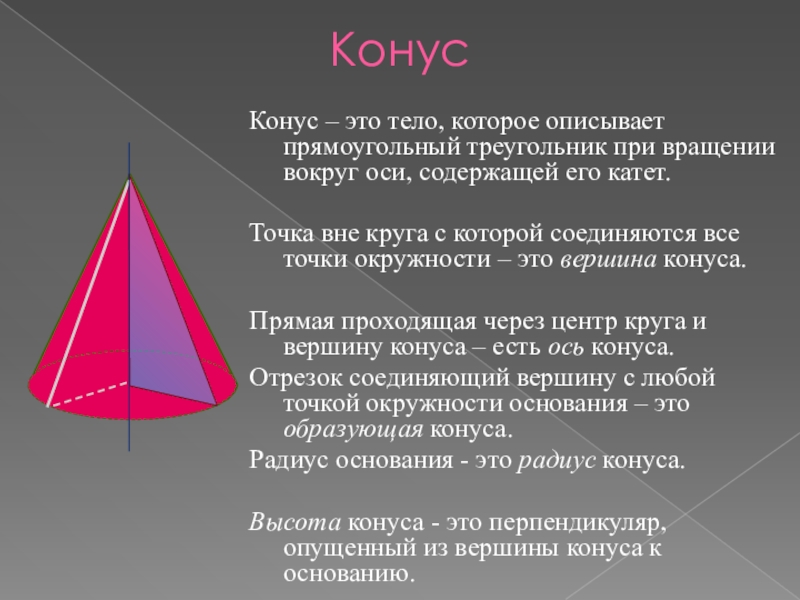
Конус – это тело, которое описывает прямоугольный треугольник при вращении
вокруг оси, содержащей его катет.
Точка вне круга с которой соединяются
все точки окружности – это вершина конуса.Прямая проходящая через центр круга и вершину конуса – есть ось конуса.
Отрезок соединяющий вершину с любой точкой окружности основания – это образующая конуса.
Радиус основания - это радиус конуса.
Высота конуса - это перпендикуляр, опущенный из вершины конуса к основанию.
Слайд 11Сечение конуса
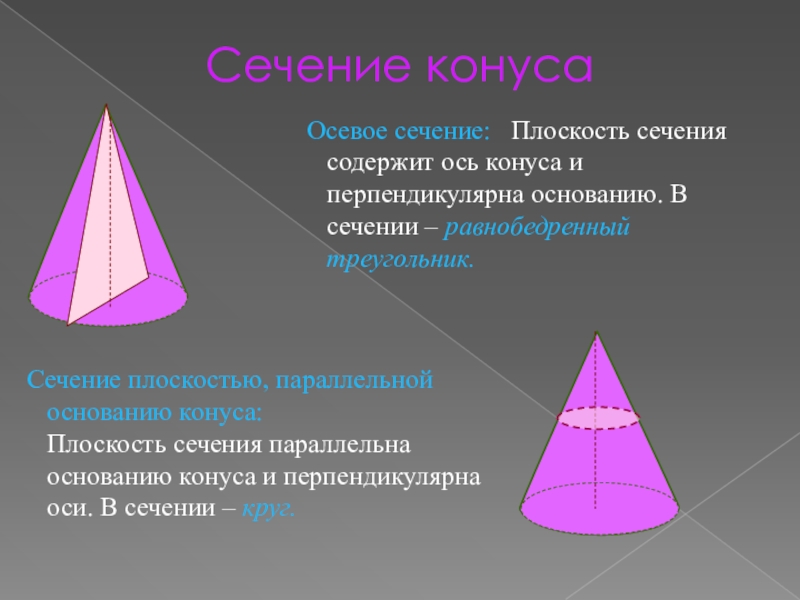
Сечение плоскостью, параллельной основанию конуса:
Плоскость сечения параллельна основанию
конуса и перпендикулярна оси. В сечении – круг.
Осевое сечение:
Плоскость сечения содержит ось конуса и перпендикулярна основанию. В сечении – равнобедренный треугольник.Слайд 12Площадь поверхности конуса
Для вывода формулы площади полной поверхности конуса потребуется
его развертка.
Полная поверхность состоит из основания и боковой поверхности.
Площадь
основания находим как площадь круга S = R2R – радиус основания цилиндра
Боковая поверхность конуса есть.
Площадь боковой поверхности конуса равна произведению радиуса на образующую и число .
Получаем, Sполн = Sбок + Sосн = Rl + R2
l
l
R
R
2R
Слайд 14Шар
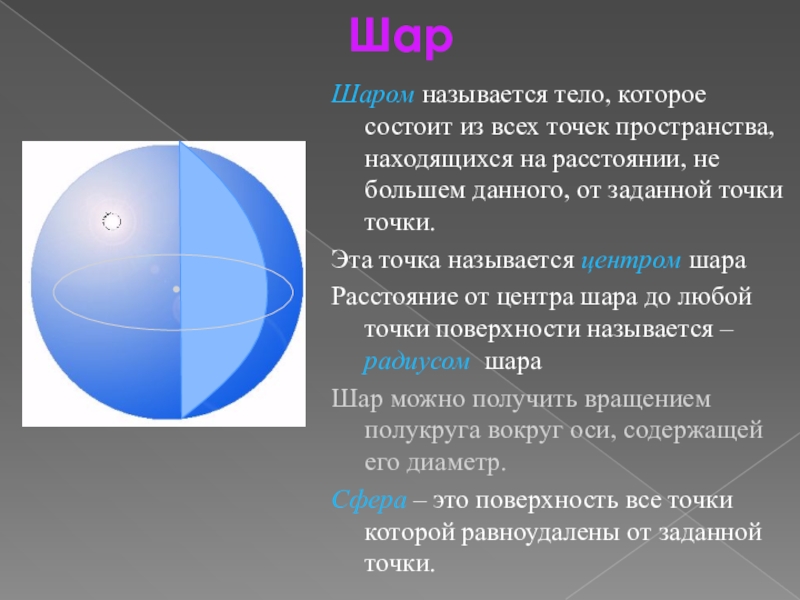
Шаром называется тело, которое состоит из всех точек пространства, находящихся
на расстоянии, не большем данного, от заданной точки точки.
Эта точка
называется центром шараРасстояние от центра шара до любой точки поверхности называется – радиусом шара
Шар можно получить вращением полукруга вокруг оси, содержащей его диаметр.
Сфера – это поверхность все точки которой равноудалены от заданной точки.
Слайд 15Сечения шара
Сечение шара, проходящее через его центр:
В сечении –круг.
В этом
случае в сечении получается круг наибольшего радиуса, его называют большой
круг шара.Сечение плоскостью, не проходящей через центр шара: В сечении – круг.
Площадь поверхности шара равна четыре площади большого круга шара:
S = 4R2
Слайд 17Задача на цилиндр
Решение.
1) Если дно шляпы опустить на плоскость её
полей, то получим круг радиуса
R = r1+ 10
= 20 cм.2) Площадь этого круга
3) Найдем площадь боковой поверхности цилиндрической части
4) Найдем площадь шляпы
Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке.
Ответ: 1600 (см2).
r1=10
10
10
Слайд 18 Задача на конус
Объем конуса равен 16. Через середину высоты
параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса
с той же вершиной. Найдите объем меньшего конуса.Ответ: 2
h
R
Слайд 19Задач на шар
Найдите длину полярного круга Земли (радиус Земли
принять за 6400 км)
1)Из справочника: длина дуги от экватора до
полярного круга 66. Этой же мере соответствует центральный угол АОВ = 66
2)Дуга от Северного полюса до экватора равна 90. Значит, СОВ = 90.
Тогда, СОА = 90 - 66 = 24.
3)Используя синус угла СОА в прямоугольном АСО найдем СА:
CA= AO· sin(COA)= 6400 · sin 24 = 6400 · 0,4067= 2602,88 (км)
4) СА есть радиус окружности полярного круга, найдем длину этой окружности:
2·CA =2· 3,14· 2602,88 = 16 346, 0864 км
Ответ: длина полярного круга ≈ 16 тыс. км
66
С
А
О
В
экватор
полярный круг
Северный полюс