Тема 1

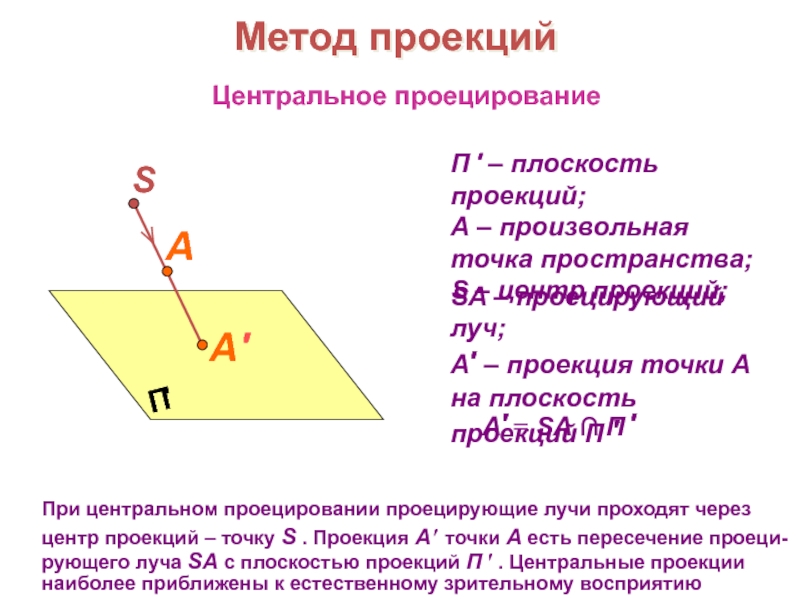
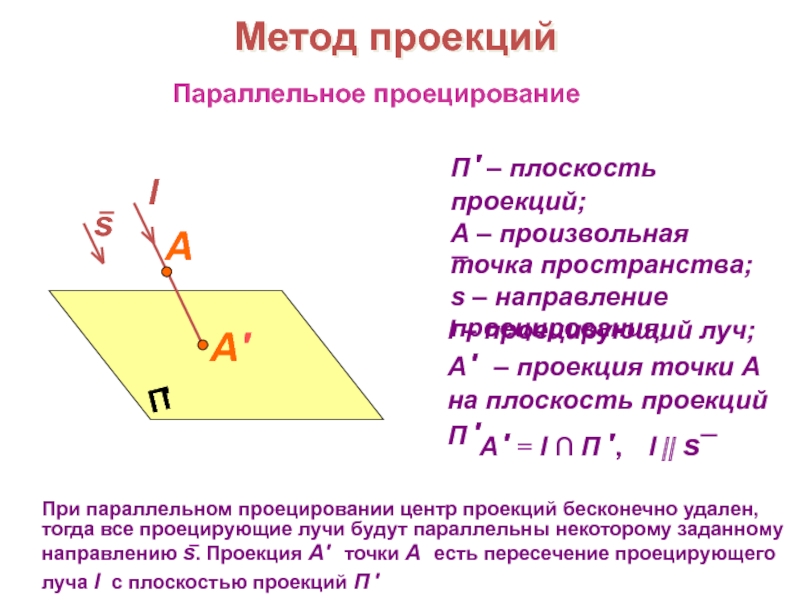
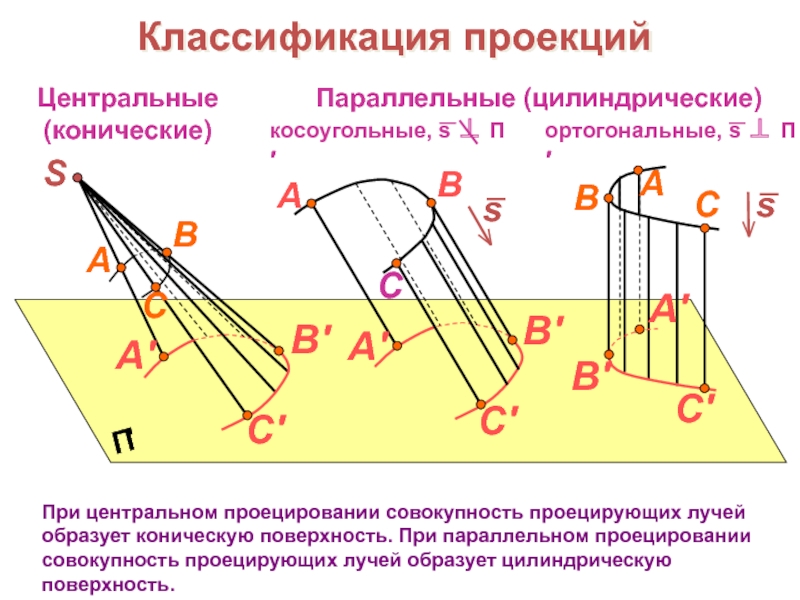
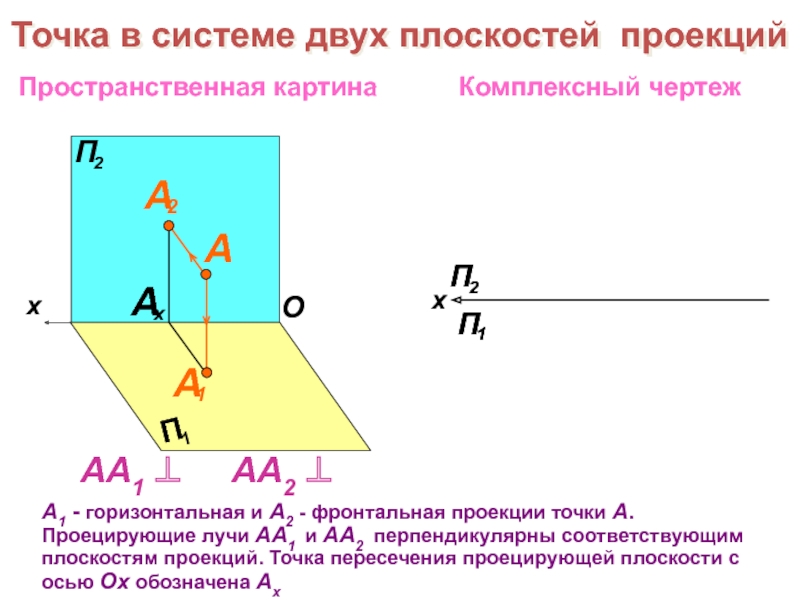
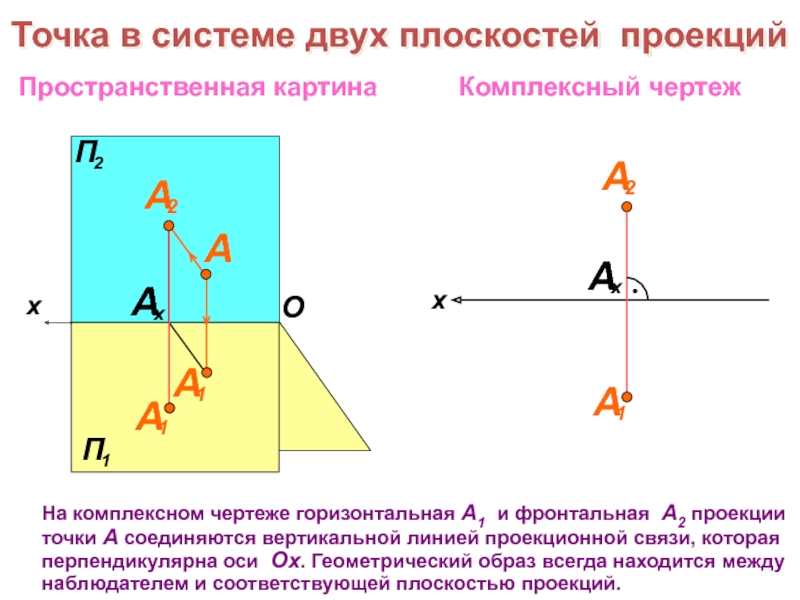
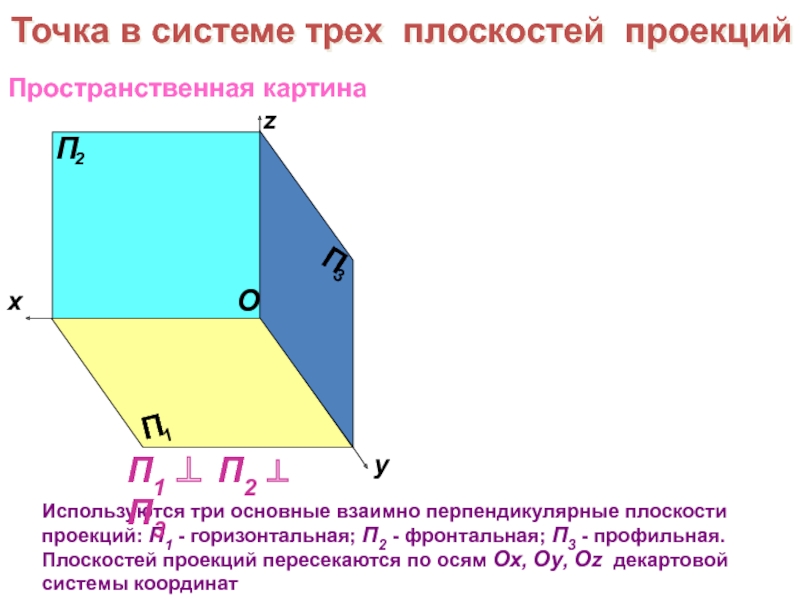
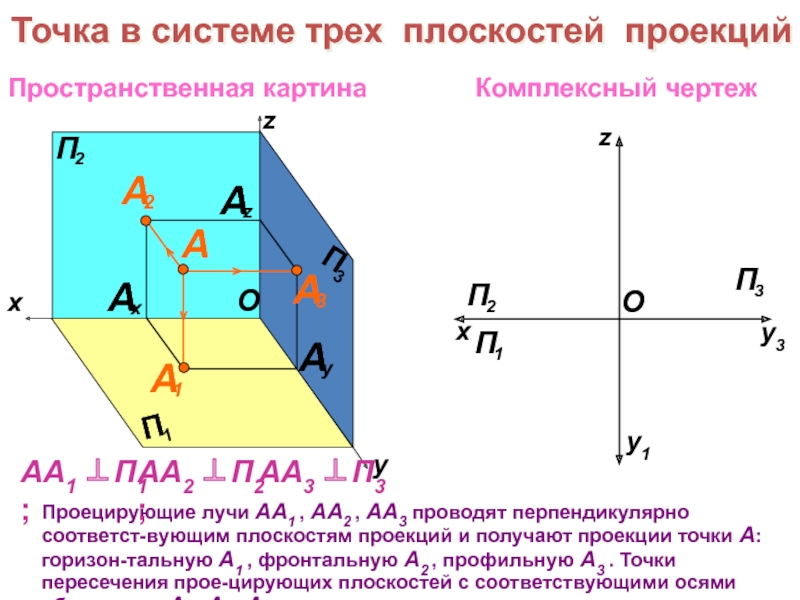
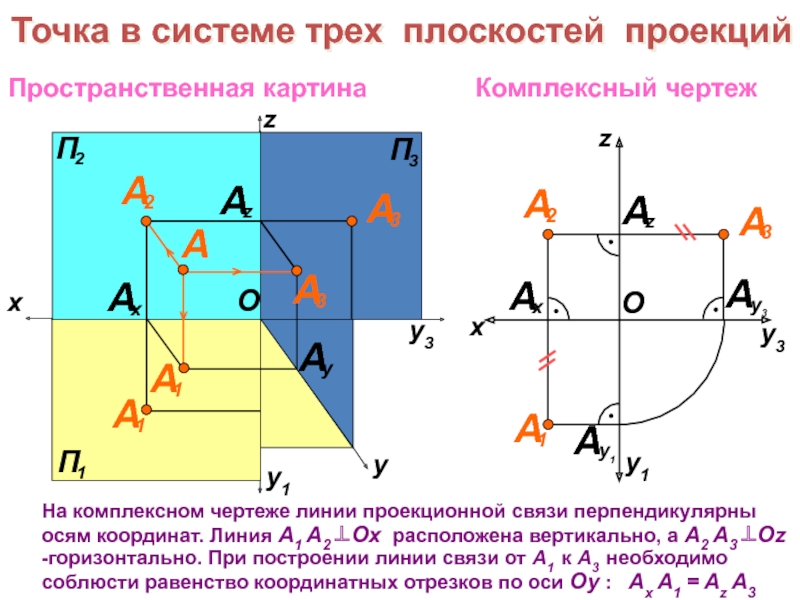
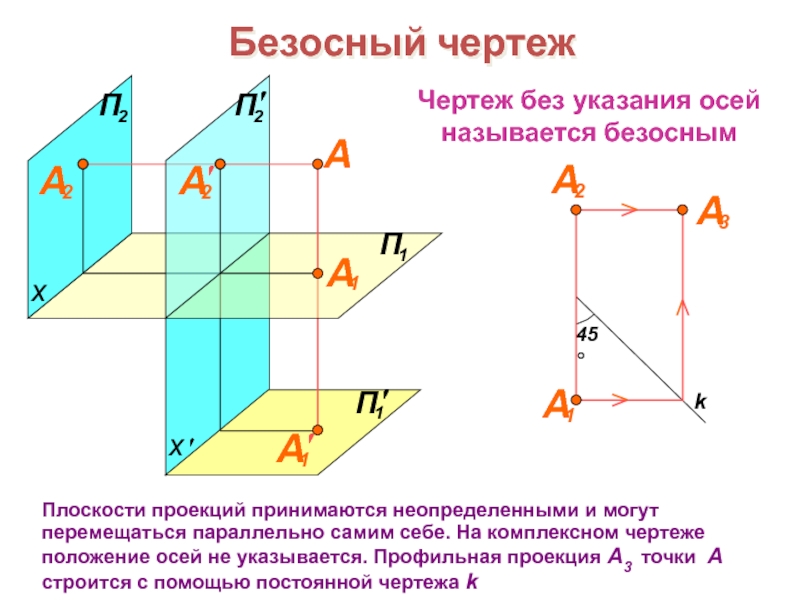
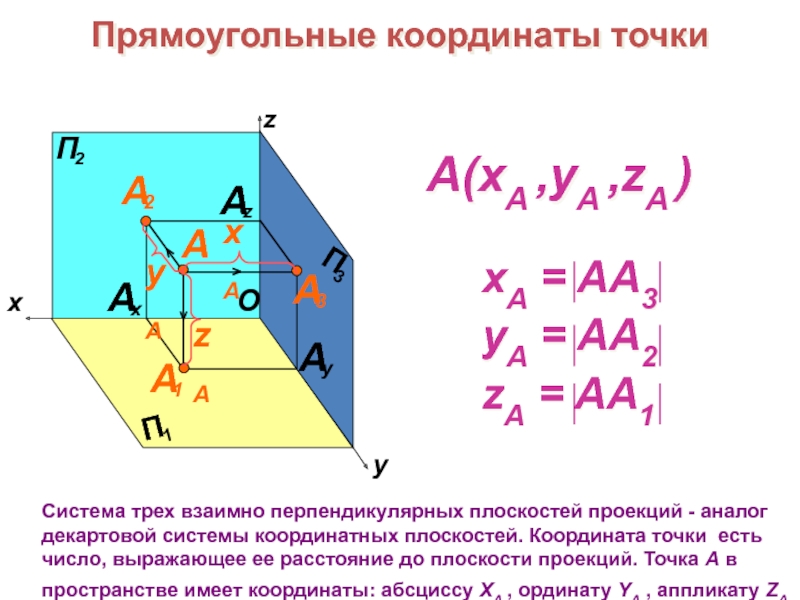
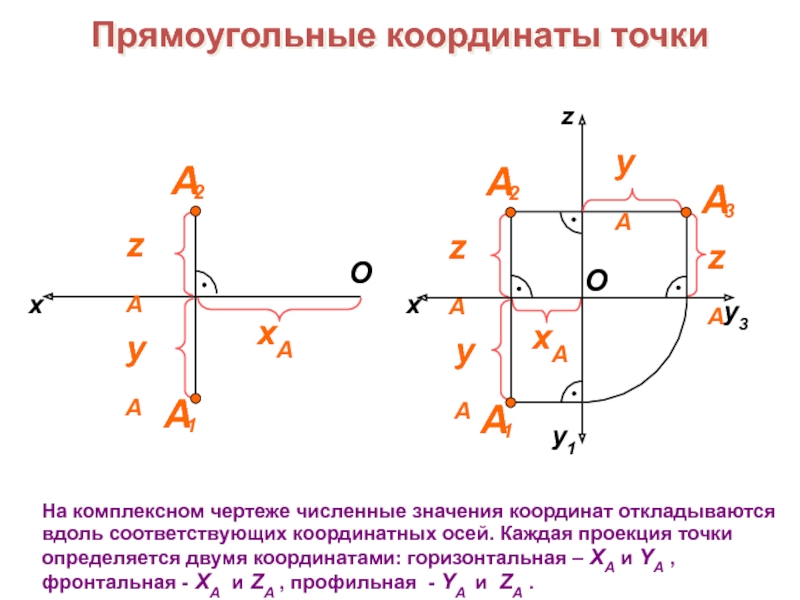
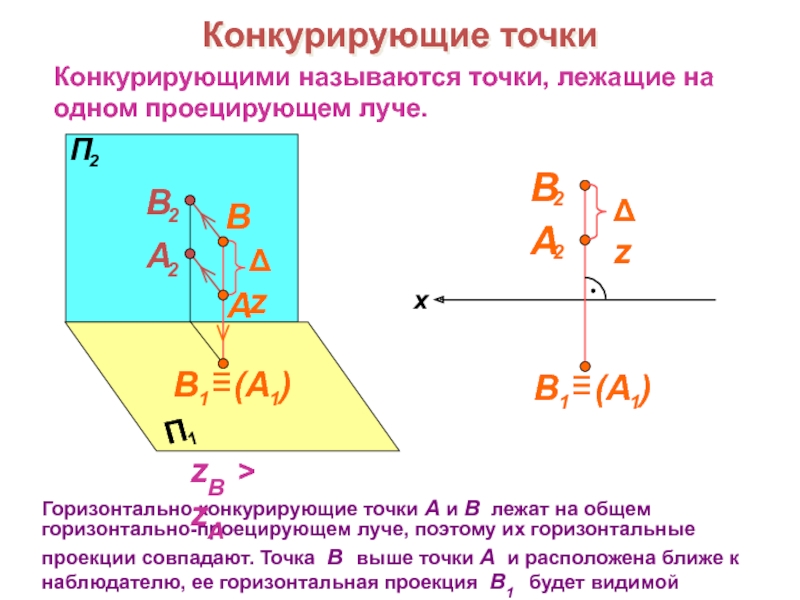
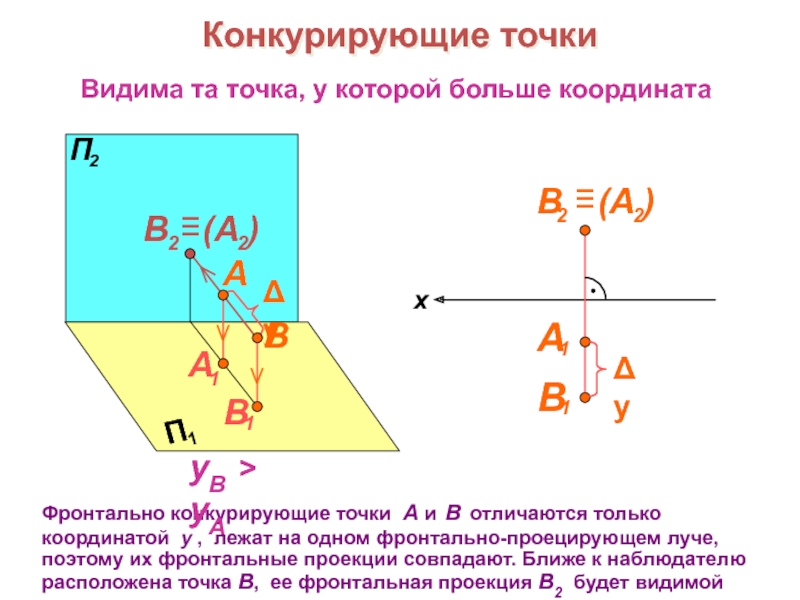
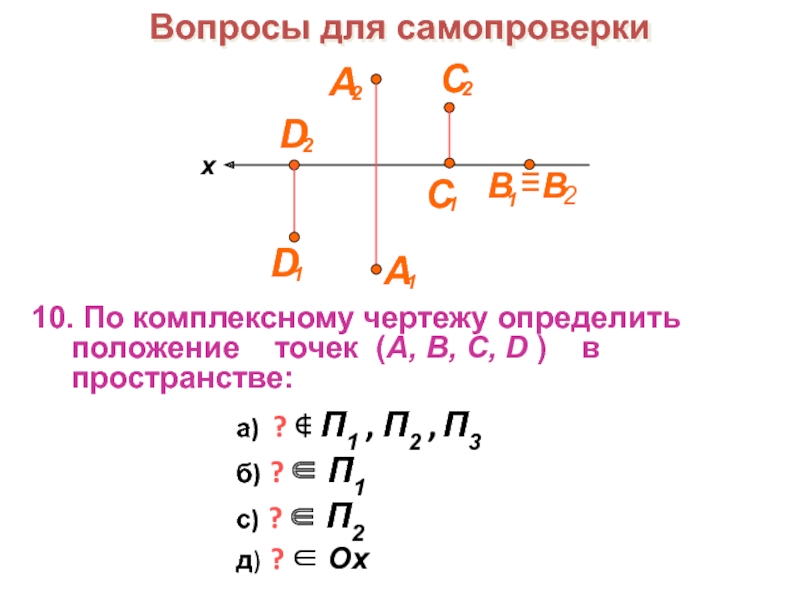
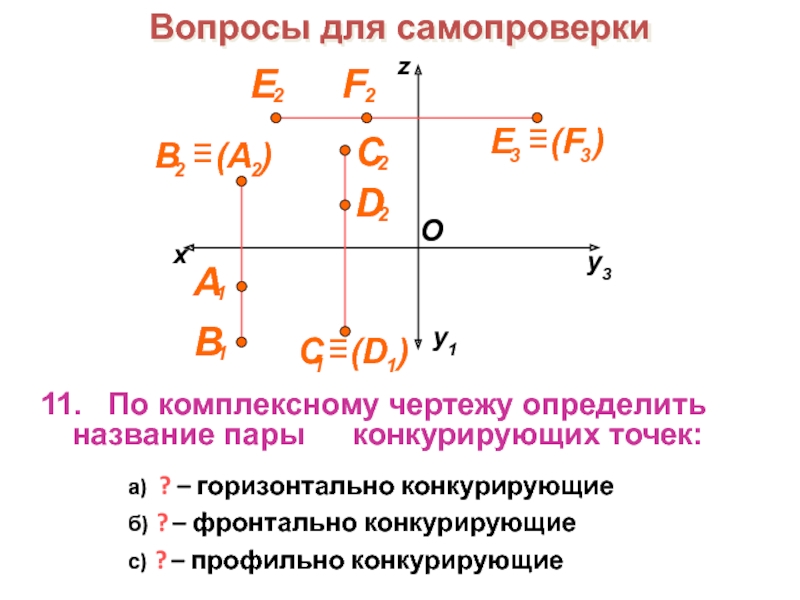
образов трехмерного пространства на плоскости чертежа
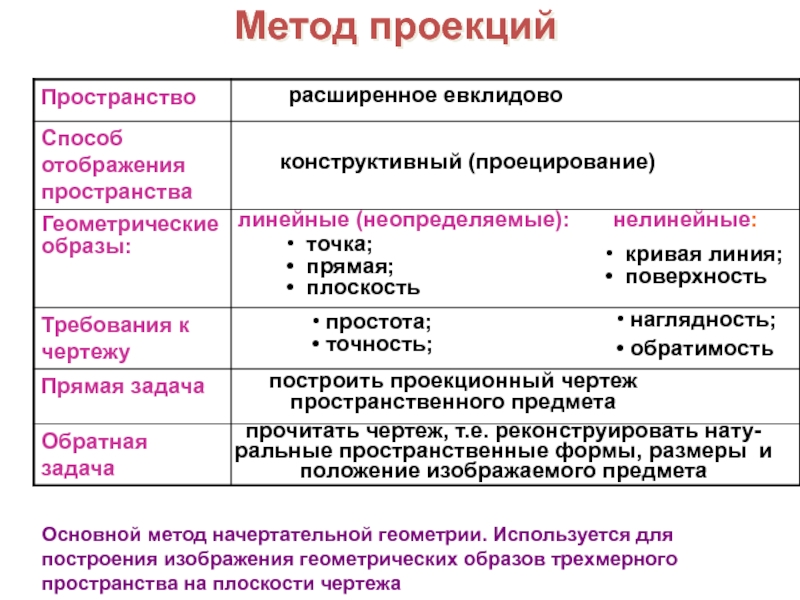
расширенное евклидово
конструктивный (проецирование)
линейные (неопределяемые):

нелинейные:

точка;
прямая;
плоскость

кривая линия;
поверхность

простота;
точность;

наглядность;
обратимость

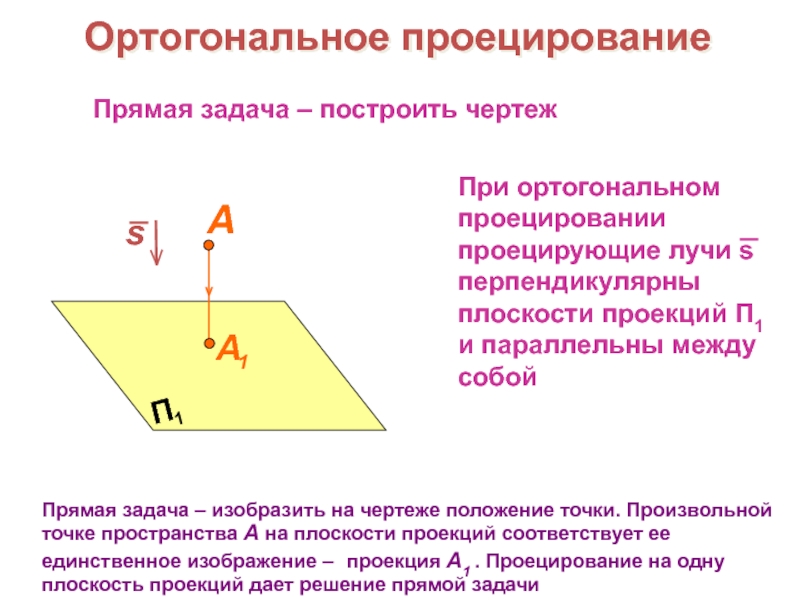
построить проекционный чертеж пространственного предмета

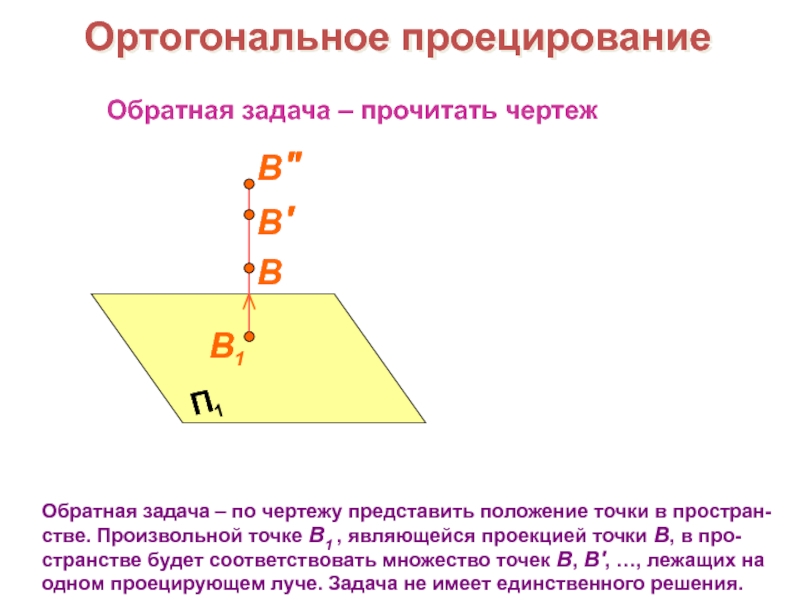
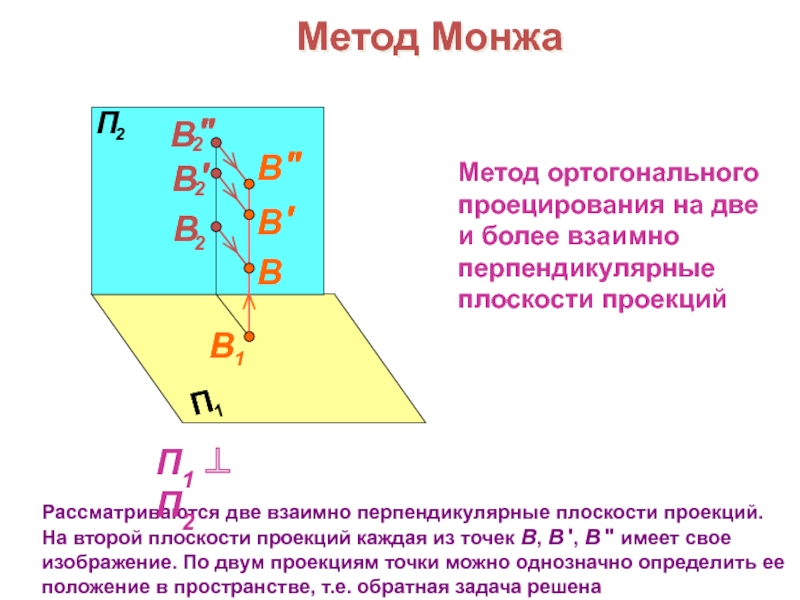
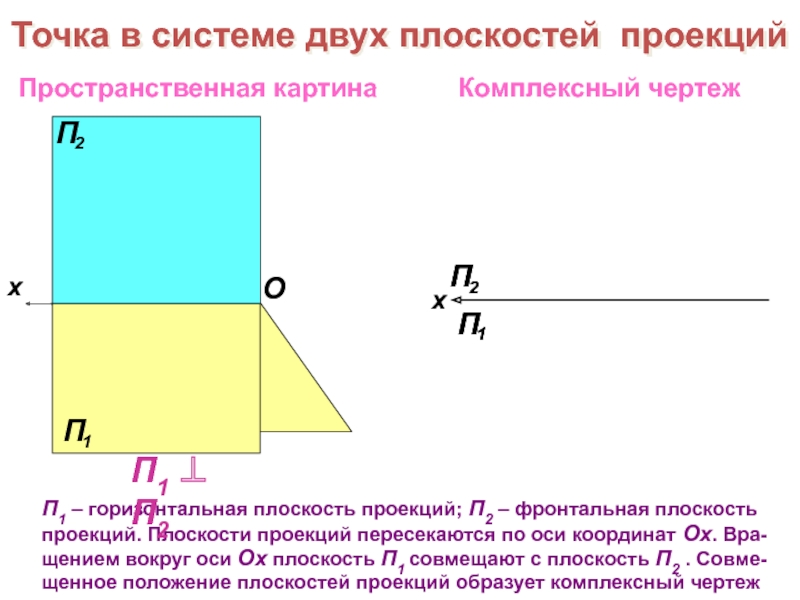
прочитать чертеж, т.е. реконструировать нату-ральные пространственные формы, размеры и положение изображаемого предмета

центр проекций;

А = SA  П 
S
При центральном проецировании проецирующие

лучи проходят через центр проекций – точку S . Проекция А точки А есть пересечение проеци-рующего луча SA с плоскостью проекций П  . Центральные проекции наиболее приближены к естественному зрительному восприятию

Центральное проецирование

Метод проекций

SA – проецирующий луч;
А – проекция точки А на плоскость проекций П 

А на плоскость проекций П 

параллельном проецировании совокупность проецирующих лучей образует цилиндрическую поверхность.
Центральные
(конические)
Классификация проекций
Параллельные

(цилиндрические)

линии, в общем случае, прямая
Каждая точка и линия в пространстве

имеют свою единственную проекцию
Если точка принадлежит прямой, то и проекция точки принадлежит проекции данной прямой
Для построения проекции прямой достаточно спроецировать две ее точки и через полученные проекции этих точек провести прямую линию

проекций
Отрезок прямой, параллельный плоскости проекций, проецируется на эту плоскость без

искажения
Проекции параллельных прямых параллельны
Отношение длин отрезков параллельных прямых равно отношению длин их проекций
При параллельном переносе плоскости проекций величина проекций не меняется

пространства А на плоскости проекций соответствует ее единственное изображение –

проекция А1 . Проецирование на одну плоскость проекций дает решение прямой задачи

Ортогональное проецирование

Прямая задача – построить чертеж

Произвольной точке В1 , являющейся проекцией точки В, в про-странстве

будет соответствовать множество точек В, В', …, лежащих на одном проецирующем луче. Задача не имеет единственного решения.

Ортогональное проецирование

Обратная задача – прочитать чертеж

каждая из точек В, В ', В " имеет свое

изображение. По двум проекциям точки можно однозначно определить ее положение в пространстве, т.е. обратная задача решена

Метод Монжа

Метод ортогонального
проецирования на две и более взаимно перпендикулярные плоскости проекций

П1  П2

плоскостях проекций
Метод ортогонального проецирования:
плоскости проекций перпендикулярны между собой;
проецирующие

лучи перпендикулярны плоскости проекций.

Метод Монжа

Для однозначного определения положения точки
в пространстве необходимо задать на чертеже
минимум две ее ортогональные проекции

Плоскости проекций пересекаются по оси координат Оx. Вра-щением вокруг оси

Ох плоскость П1 совмещают с плоскость П2 . Совме-щенное положение плоскостей проекций образует комплексный чертеж

Точка в системе двух плоскостей проекций

Пространственная картина

П1  П2

и А2 - фронтальная проекции точки А. Проецирующие лучи АА1

и АА2 перпендикулярны соответствующим плоскостям проекций. Точка пересечения проецирующей плоскости с осью Оx обозначена Ах

горизонтальная А1 и фронтальная А2 проекции точки А соединяются вертикальной

линией проекционной связи, которая перпендикулярна оси Ох. Геометрический образ всегда находится между наблюдателем и соответствующей плоскостью проекций.

П2 - фронтальная; П3 - профильная. Плоскостей проекций пересекаются по

осям Оx, Оy, Оz декартовой системы координат

Пространственная картина

Точка в системе трех плоскостей проекций

Оy и совмещают все три плоскости проекций в одну: П1

поворачивают вокруг оси Оx, П3 поворачивают вокруг оси Оz до их совпадения с П2 . Ось Оу распадается на две оси y1 и y3

O

Точка в системе трех плоскостей проекций

Пространственная картина

плоскостям проекций и получают проекции точки А: горизон-тальную А1 ,

фронтальную А2 , профильную А3 . Точки пересечения прое-цирующих плоскостей с соответствующими осями обозначены Ах , Аy , Аz

x

z

O

Точка в системе трех плоскостей проекций

Пространственная картина

Комплексный чертеж

А1 А2 Ох расположена вертикально, а А2 А3 Оz -горизонтально.

При построении линии связи от А1 к А3 необходимо соблюсти равенство координатных отрезков по оси Оy : Ax A1 = Az A3

O

y3

x

z

y1

z

Точка в системе трех плоскостей проекций

Пространственная картина

Комплексный чертеж

O

себе. На комплексном чертеже положение осей не указывается. Профильная проекция

А3 точки А строится с помощью постоянной чертежа k

Чертеж без указания осей
называется безосным

проекций - аналог декартовой системы координатных плоскостей. Координата точки есть

число, выражающее ее расстояние до плоскости проекций. Точка А в пространстве имеет координаты: абсциссу XA , ординату YA , аппликату ZA

соответствующих координатных осей. Каждая проекция точки определяется двумя координатами: горизонтальная

– XA и YA , фронтальная - XA и ZA , профильная - YA и ZA .

x

O

точки А и В лежат на общем горизонтально-проецирующем луче, поэтому

их горизонтальные проекции совпадают. Точка В выше точки А и расположена ближе к наблюдателю, ее горизонтальная проекция В1 будет видимой

zB > zA

y , лежат на одном фронтально-проецирующем луче, поэтому их фронтальные

проекции совпадают. Ближе к наблюдателю расположена точка В, ее фронтальная проекция В2 будет видимой

A

В

yB > yA

Видима та точка, у которой больше координата

б) параллельные
Где расположен центр проекций при параллельном проецировании?
а) на

плоскости проекций
б) в бесконечности
Сколько плоскостей проекций нужно использовать для обратимости чертежа?
а) одну
б) две
в) три
Какой способ проецирования используется в методе Монжа?
а) центральный
б) ортогональный
в) косоугольный
Какое минимальное количество проекций точки достаточно задать на комплексном чертеже?
а) одну
б) две
в) три

а) x и y
б) y и z
в)

x и z
7. Какие координаты определяют фронтальную проекцию точки?
а) x и y
б) y и z
в) x и z
8. Какие координаты определяют профильную проекцию точки?
а) x и y
б) y и z
в) x и z
9. Сколько одинаковых координат имеют конкурирующие точки?
а) все
б) одну
в) две

(A, B, C, D ) в пространстве:
а)

?  П1 , П2 , П3
б) ?  П1
с) ?  П2
д) ?  Ox

пары конкурирующих точек:
а) ? – горизонтально конкурирующие
б)

? – фронтально конкурирующие
с) ? – профильно конкурирующие