Слайд 1Алгоритмизация и программирование
Тема 1
Алгоритм и его свойства.
Способы записи алгоритма
Слайд 2Понятие алгоритма
Алгоритм – это четкое описание
последовательности действий, которые
необходимо выполнить для
решения задачи
Свойства алгоритма
1) Дискретность
2) Определенность (или детерминированность)
3) Результативность
(или конечность)
4) Массовость
Слайд 3Понятие алгоритма
Алгоритм – это четкое описание
последовательности действий, которые
необходимо выполнить для
решения задачи
Формы представления алгоритма
1) Словесная
2) Графическая
3) Запись
на специальном языке (алгоритмическом языке или псевдокоде)
Слайд 4 Описание последовательных этапов обработки данных на естественном языке
Алгоритм Евклида
1)
задать два числа;
2) если числа равны, то взять любое из
них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
3) определить большее из чисел;
4) заменить большее из чисел разностью большего и меньшего из чисел;
5) повторить алгоритм с шага 2
Словесный способ
Слайд 5Графическое представление алгоритма называется схемой алгоритма
или блок-схемой
Графический способ
Слайд 6Основные элементы
блок-схемы алгоритма
ГОСТ 19.701-90
«Единая система программной документации.
Схемы алгоритмов, программ, данных
и систем.
Обозначения условные и правила выполнения»
Графический способ
Слайд 7Графический способ
Терминатор
Основные элементы блок-схемы алгоритма
Слайд 8Графический способ
Данные
Основные элементы блок-схемы алгоритма
Слайд 9Графический способ
Процесс
Основные элементы блок-схемы алгоритма
Слайд 10Графический способ
Решение
Основные элементы блок-схемы алгоритма
Слайд 11Графический способ
Предопределённый процесс
Основные элементы блок-схемы алгоритма
Слайд 12Графический способ
Дисплей
Основные элементы блок-схемы алгоритма
Слайд 13Графический способ
Ручной ввод
Основные элементы блок-схемы алгоритма
Слайд 14Основные элементы блок-схемы алгоритма
Графический способ
Граница цикла
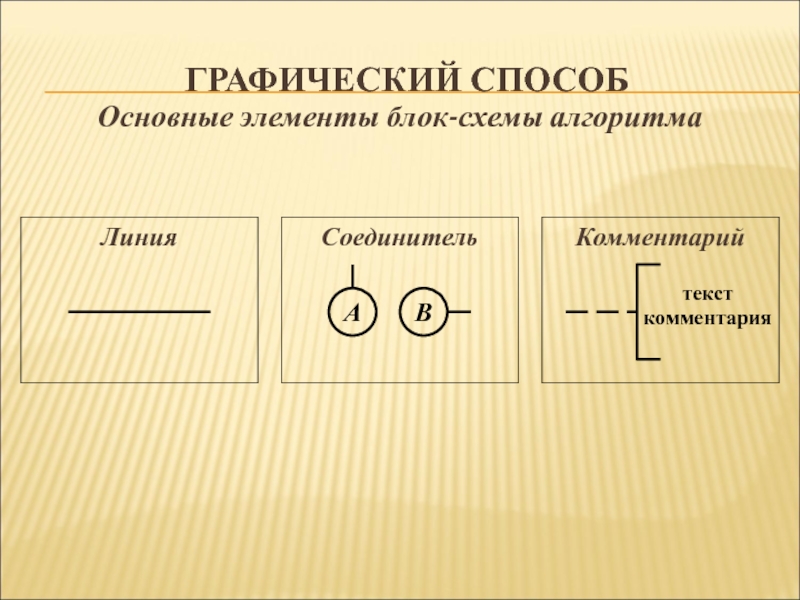
Слайд 15Графический способ
Линия
Соединитель
Комментарий
Основные элементы блок-схемы алгоритма
Слайд 16Алгоритмические языки
ab ab ab a*b
Пример псевдокода
алг (алгоритм) сим (символьный) дано для да
арг (аргумент) лит (литерный) надо от нет
рез (результат) лог (логический) если до при
нач
(начало) таб (таблица) то знач выбор
кон (конец) нц (начало цикла) иначе и ввод
цел (целый) кц (конец цикла) все или вывод
вещ (вещественный) длин (длина) пока не утв
Слайд 17Общий вид алгоритма
алг название алгоритма (аргументы и результаты)
нач описание
промежуточных величин
| последовательность команд (тело алгоритма)
кон
Примеры предложений алг:
алг объем_и_площадь_цилиндра (арг вещ
R, H, рез вещ V, S)
алг диагональ (арг цел N, арг цел таб A[1:N, 1:N], рез лит otvet)
Слайд 18Пример записи
на алгоритмическом языке
алг произведение (арг цел n, m,
рез цел s)
нач цел i
| ввод n, m
| s:=0
| i:=0
| нц пока i
Слайд 19Тема 2
базовые алгоритмические структуры
Слайд 20 1) Линейная
2) Разветвляющаяся
3) Циклическая
Базовые структуры алгоритмов
Слайд 21Линейная алгоритмическая структура
Образуется последовательностью действий, следующих одно за другим:
Слайд 22Линейная алгоритмическая структура (пример)
алг сумма (арг вещ a, b, рез
вещ s)
нач
| ввод a, b
| s:=a+b
| вывод s
кон
Слайд 23Разветвляющаяся алгоритмическая структура
Обеспечивает в зависимости
от результата проверки условия
выбор одного
из альтернативных путей
работы алгоритма
Виды ветвлений
1) ветвление (если-то-иначе)
2) множественный выбор
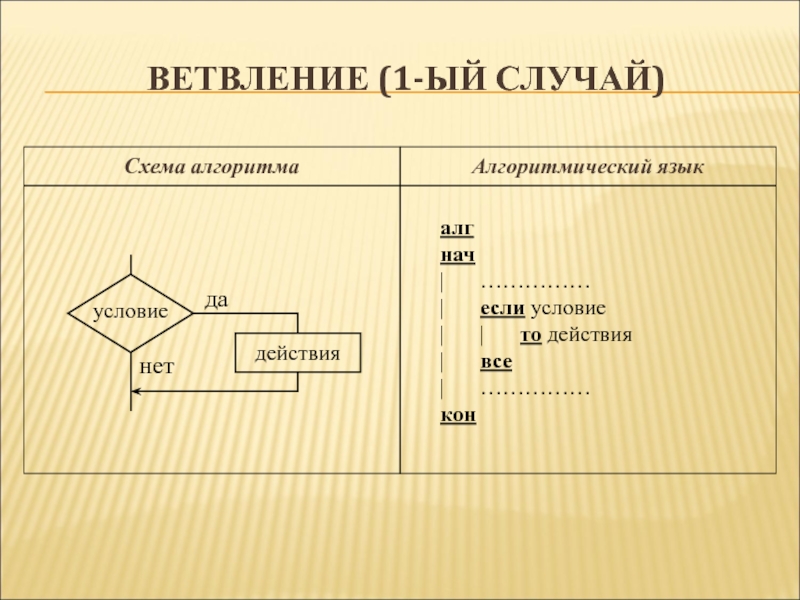
Слайд 24Ветвление (1-ый случай)
алг
нач
| ……………
| если условие
| | то действия
| все
| ……………
кон
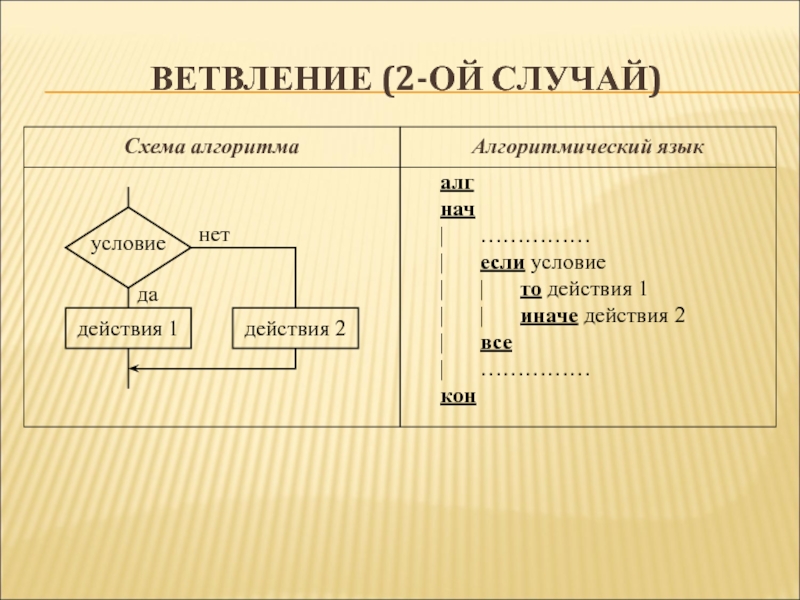
Слайд 25Ветвление (2-ой случай)
алг
нач
| ……………
| если условие
| | то действия 1
| | иначе действия 2
| все
| ……………
кон
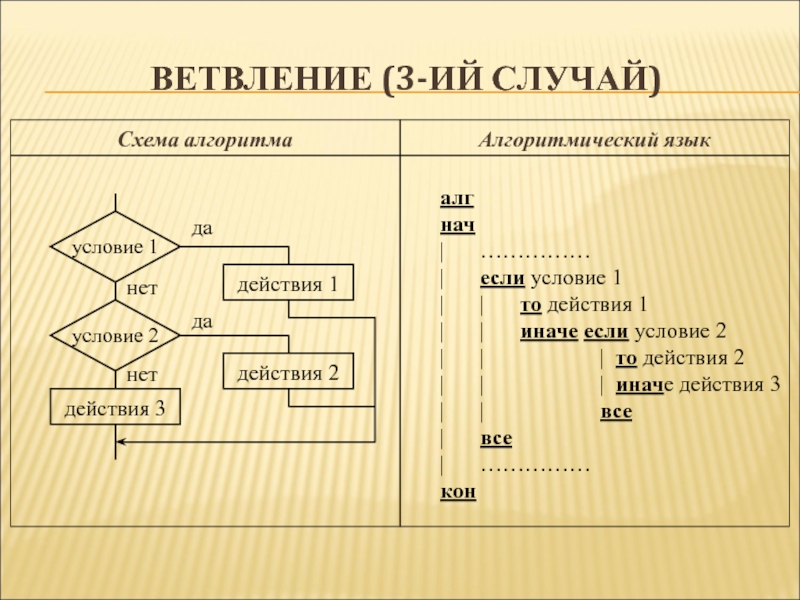
Слайд 26Ветвление (3-ий случай)
алг
нач
| ……………
| если условие 1
| | то действия 1
| | иначе если условие 2
| | |
то действия 2
| | | иначе действия 3
| | все
| все
| ……………
кон
Слайд 27Множественный выбор
алг
нач
| ……………
| выбор i
| | при альт. 1: действия 1
| | ……………
| | при альт. n: действия
n
| | иначе действия n+1
| все
| ……………
кон
Слайд 28Циклическая алгоритмическая структура
Обеспечивает многократное выполнение
некоторой совокупности действий,
которая называется телом цикла
Виды
циклов
1) Цикл с предусловием
2) Цикл с постусловием
3) Цикл со счётчиком
(с известным количеством повторений)
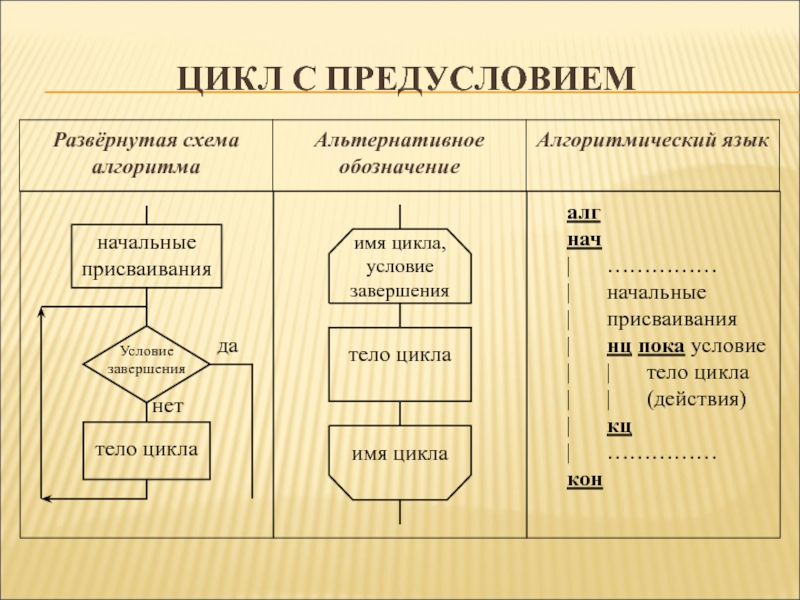
Слайд 29Цикл с предусловием
алг
нач
| ……………
| начальные
| присваивания
| нц пока условие
| | тело цикла
| | (действия)
| кц
| ……………
кон
Слайд 30Цикл с постусловием
алг
нач
| ……………
| начальные
| присваивания
| нц
| | тело цикла
| | (действия)
| кц пока условие
| ……………
кон
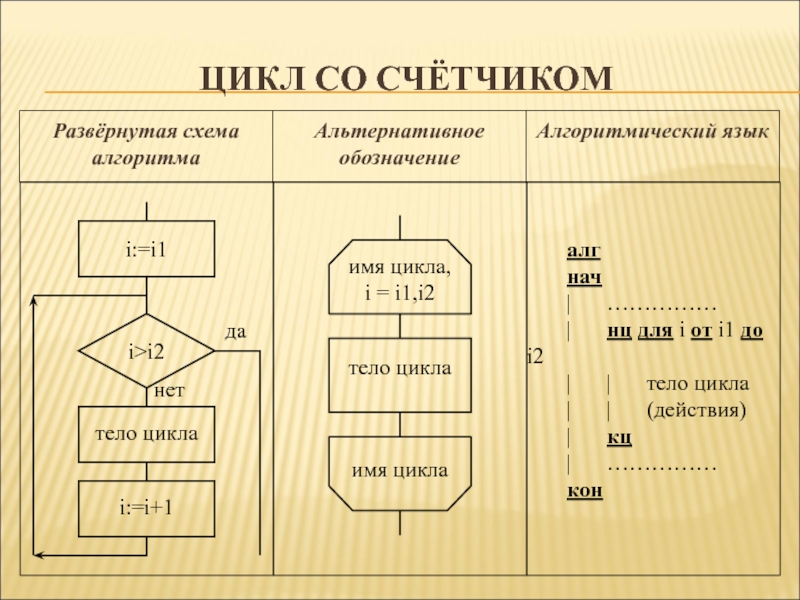
Слайд 31Цикл со счётчиком
алг
нач
| ……………
| нц для i от i1 до i2
| | тело цикла
| | (действия)
| кц
| ……………
кон
Слайд 33Алгоритм поиска минимума в массиве,
состоящего из трёх элементов (схема)
Конец
Слайд 34Алгоритм поиска минимума в массиве,
состоящего из трёх элементов (псевдокод)
алг мин
(арг вещ таб X[1:3], рез вещ min, рез цел num)
нач
| ввод
X
| если X[2] | | то min:=X[2], num:=2
| | иначе min:=X[1], num:=1
| все
| если X[3] | | то min:=X[3], num:=3
| все
| вывод min, num
кон
Слайд 35Алгоритм циклического сдвига одномерного массива на один шаг вправо (схема)
Конец
A
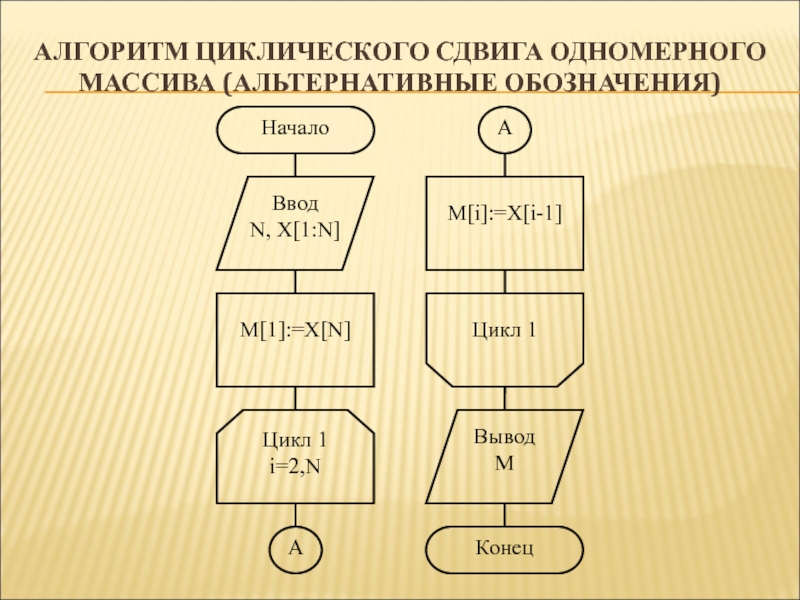
Слайд 36Алгоритм циклического сдвига одномерного массива (альтернативные обозначения)
Слайд 37Алгоритм циклического сдвига одномерного массива на один шаг вправо (псевдокод)
алг
сдвиг (арг цел N, арг таб вещ X[1:N], рез таб
вещ M[1:N])
нач цел i
| ввод N, X
| M[1]:=X[N]
| нц для i от 2 до N
| | M[i]:=X[i-1]
| кц
| вывод M
кон
Слайд 38Алгоритм сортировки по возрастанию одномерного массива методом «пузырька» (псевдокод)
алг сорт
(арг таб цел N, арг таб вещ X[1:N], рез таб
вещ M[1:N])
нач цел i, k
| ввод N, X[1:N]
| M[1:N]:=X[1:N]
| k:=1 //признак упорядоченности массива: k:=1 - массив не упорядочен
| нц пока k=1
| | k:=0
| | нц для i от 2 до N
| | | если M[i-1]>M[i]
| | | | то b:=M[i], M[i]:=M[i-1], M[i-1]:=b, k:=1
| | | все
| | кц
| кц
| вывод M
кон
Слайд 39Алгоритм сортировки по возрастанию
одномерного массива методом «пузырька»
Развёрнутая схема алгоритма
Схема
алгоритма с альтернативными
обозначениями циклов
Самостоятельно
Слайд 41Обращение к подпрограммам
Пример алгоритма, содержащего подпрограммы:
алг Alg(арг вещ X, Y,
Z, рез вещ D)
нач
| ввод X, Y, Z
| A:=F1(X)
| B:=F2(Y,Z)
| C:=F2(A,B)
| D:=A+B+C
| вывод D
кон
Слайд 42Обращение к подпрограммам
Подпрограммы, входящие в алгоритм:
алг F1(арг вещ Arg, рез
вещ Res)
нач
| Res:=Arg*Arg
кон
алг F2(арг вещ Arg1, Arg2, рез вещ Res)
нач
| Res:=Arg1*Arg2
кон
Слайд 43Понятие рекурсии
Рекурсивным называется алгоритм
(или функция), содержащий в себе
вызов самого себя (обращение к самому себе)
Простая рекурсия:
a:=a+1
Пример рекурсии:
вычисление факториала
N!
= 1·2·3·…·N, N ≥ 0,
0! = 1 – условие выхода из рекурсии
Слайд 44Вычисление факториала
алг Факториал(арг цел N, рез цел F)
нач
| если N=0
| | то F:=1
| | иначе
F:=Факториал (N-1)*N
| все
кон
алг
нач
| A:=Факториал (5)
| вывод A
кон
Слайд 45Виды рекурсии
1) Прямая
обращение к самому себе содержится в самом
алгоритме (функции)
2) Косвенная
обращение к данному алгоритму (функции) содержится в
другом алгоритме (функции), к которому данный алгоритм имеет обращение
![Алгоритм поиска минимума в массиве, состоящего из трёх элементов (псевдокод) алг мин (арг вещ таб X[1:3], рез вещ](/img/thumbs/d42360540248a6728fc862b13e8885b3-800x.jpg "Тема 1 Алгоритм и его свойства. Способы записи алгоритма Алгоритм поиска минимума в массиве, состоящего из трёх элементов (псевдокод) алг мин")
