Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 19 Электромагнитная индукция. Закон индукции Фарадея и правило Ленца
Содержание
- 1. Тема 19 Электромагнитная индукция. Закон индукции Фарадея и правило Ленца
- 2. ОГЛАВЛЕНИЕ19.1. Электромагнитная индукция. Закон индукции Фарадея и
- 3. 19.1. Электромагнитная индукцияИзменяющееся магнитное поле вызывает появление
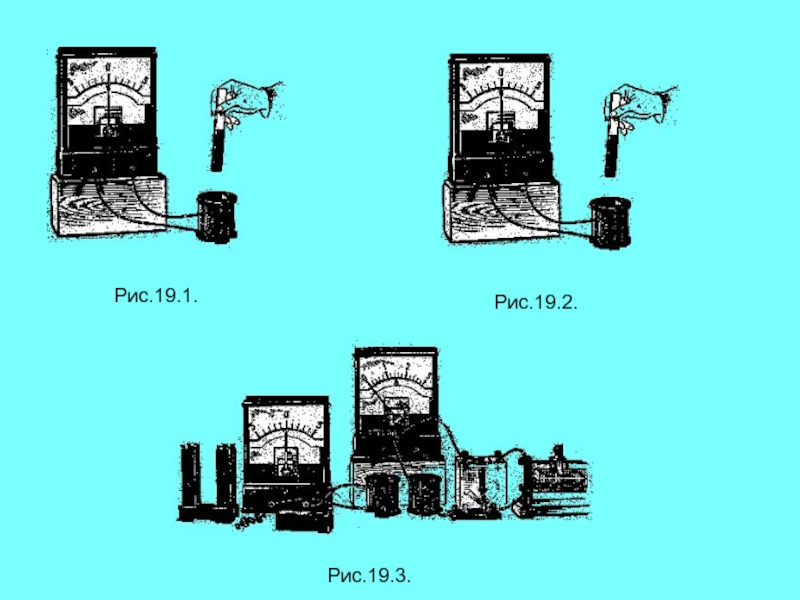
- 4. Рис.19.1.Рис.19.2.Рис.19.3.
- 5. Ход работы:1.Возьмем соленоид, соединенный с гальванометром ,
- 6. 4. Включим первичную катушку в сеть переменного
- 7. ЭДС электромагнитной индукции в контуре пропорциональна и
- 8. Направление индукционного тока можно определить по правилу
- 9. Поясним правило Ленца на следующей
- 10. В электромагнетизме для характеристики свойств проводника возбуждать
- 11. Вычислим индуктивность соленоида. Возьмем соленоид такой длины,
- 12. 19.2. Самоиндукция и взаимоиндукцияРассмотрим явление самоиндукции. Так
- 13. Возьмем два контура 1 и 2, расположенные
- 14. Аналогично, при протекании в контуре 2 тока
- 15. 19.3. Энергия и плотность энергии магнитного поля
- 16. По закону сохранения и превращения энергии совершенная работа равна энергии магнитного поля соленоида, т. е.К оглавлению(19.14)(19.15)I
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема 19
Электромагнитная индукция. Закон индукции Фарадея и правило Ленца. Самоиндукция
и взаимоиндукция. Энергия и плотность энергии магнитного поля
Слайд 2ОГЛАВЛЕНИЕ
19.1. Электромагнитная индукция. Закон индукции Фарадея и правило Ленца.
19.2. Самоиндукция
и взаимоиндукция
19.3. Энергия и плотность энергии магнитного поля
Слайд 319.1. Электромагнитная индукция
Изменяющееся магнитное поле вызывает появление ЭДС индукции Еинд.
Это явление Фарадей назвал электромагнитной индукцией. Под влиянием ЭДС индукции
в замкнутом проводнике возникает электрический ток. Опыт 19.1. Явление электромагнитной индукции
Оборудование:
Гальванометр от демонстрационного вольтметра.
Амперметр демонстрационный.
Магнит дугообразный.
Магнит прямой.
Трансформатор универсальный.
Реостат на 50 Ом.
Выключатель демонстрационный.
Штатив универсальный.
Батарея аккумуляторов.
Провода соединительные.
Ящик - подставка.
Слайд 5Ход работы:
1.Возьмем соленоид, соединенный с гальванометром , и будем вдвигать
в него постоянный магнит. Оказывается, что при движении магнита стрелка
гальванометра отклоняется. Если же магнит останавливается, то стрелка гальванометра возвращается в нулевое положение. То же самое получается при выдвижении магнита из соленоида или при надевании соленоида на неподвижный магнит. Такие опыты показывают, что индукционный ток возникает в соленоиде только при относительном перемещении соленоида и магнита.2. Будем опускать в соленоид катушку с током. Оказывается, что и в этом случае в соленоиде возникает индукционный ток только при относительном перемещении соленоида и катушки.
3. Вставим катушку в соленоид и закрепим их неподвижно. При этом тока в соленоиде нет. Но в моменты замыкания или размыкания цепи катушки А в соленоиде появляется индукционный ток. То же самое получается в моменты усиления или ослабления тока в катушке с помощью изменения сопротивления R. В дальнейшем цепь катушки , соединенную с источником электрической энергии, будем называть первичной, а цепь соленоида, в которой возникает индукционный ток, – вторичной. Эти же названия будем применять и к самим катушкам.
Слайд 64. Включим первичную катушку в сеть переменного тока, а вторичную
катушку соединим с лампой накаливания. Оказывается, лампа непрерывно горит, пока
в первичной катушке течет переменный ток. Нетрудно заметить, что общим для всех описанных опытов является изменение магнитного поля в соленоиде, которое и создает в нем индукционный ток. 5.Выясним теперь, всякое ли изменение магнитного поля вокруг замкнутого контура наводит в нем индукционный ток. Возьмем плоский контур в виде рамки, соединенной с гальванометром. Поместим рядом с рамкой магнит так, чтобы его линии индукции не проходили внутри рамки, а находились в ее плоскости. Оказывается, что при перемещении рамки или магнита вдоль плоскости рисунка стрелка гальванометра не отклоняется. Если же рамку поворачивать вокруг оси, то в ней возникает индукционный ток.Вывод: индукционный ток (и э. д. с. индукции) в замкнутом контуре появляется только в том случае, когда изменяется магнитный поток, который проводит через площадь, охваченную контуром.
Слайд 7ЭДС электромагнитной индукции в контуре пропорциональна и противоположна по знаку
скорости изменения магнитного потока сквозь поверхность, натянутую на контур.
В свою
очередь, магнитный поток имеет две компоненты: потокосцепление и поток рассеяния Фрас, т. е.
- потокосцепление,
Фрас – поток рассеивания.
Потокосцепление - это часть магнитного потока, пронизывающего объем проводника. Поток рассеяния Фрас – это часть магнитного потока, не связанного с проводником, а пронизывающего окружающее пространство.
(19.1)
(19.2)
(19.3)
- магнитный поток
Где
Слайд 8Направление индукционного тока можно определить по правилу Ленца, которое гласит,
что индукционный ток всегда препятствует причине, его порождающей.
Опыт 19.2.
Правило Ленца Оборудование:
Прибор для демонстрации правила Ленца.
Магнит прямой.
Рис.19.4.
Ход работы:
1.Будем вдвигать магнит в сплошное кольцо коромысла. Кольцо отталкивается от магнита, что приводит к вращению коромысла. 2.Введем магнит внутрь сплошного кольца и будем магнит выводить. Кольцо будет притягиваться к магниту, что приведет к вращению коромысла.
3.Будем вводить (или выводить) магнит внутрь разрезанного кольца. Коромысло остается в покое.
Вывод: Магнитное поле индукционного тока всегда противодействует изменению внешнего магнитного потока. В случае с разрезанным кольцом индукционный ток отсутствовал. Следовательно, отсутствовало и взаимодействие кольца с магнитом.
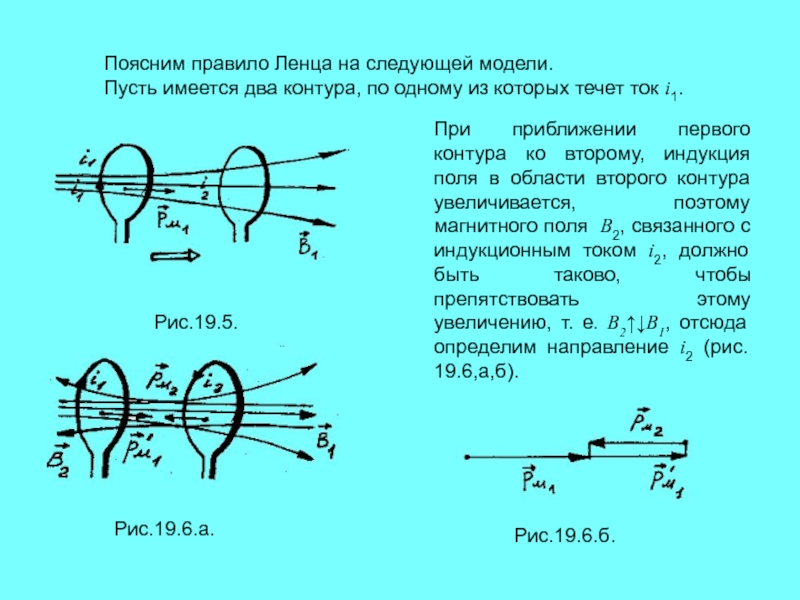
Слайд 9 Поясним правило Ленца на следующей модели.
Пусть
имеется два контура, по одному из которых течет ток i1.
Рис.19.5.
При
приближении первого контура ко второму, индукция поля в области второго контура увеличивается, поэтому магнитного поля В2, связанного с индукционным током i2, должно быть таково, чтобы препятствовать этому увеличению, т. е. В2↑↓В1, отсюда определим направление i2 (рис. 19.6,а,б).Рис.19.6.а.
Рис.19.6.б.
Слайд 10В электромагнетизме для характеристики свойств проводника возбуждать вокруг себя то
или иное магнитное поле вводится понятие индуктивности проводника (в некотором
смысле это аналогично введению понятия электроемкости в электростатике).Итак,
(19.4)
– индуктивность проводника.
Индуктивностью называется физическая величина, которая численно равна потоку сцепления при силе тока в проводнике в 1 Ампер.
Слайд 11Вычислим индуктивность соленоида. Возьмем соленоид такой длины, чтобы его можно
было практически считать бесконечным. При протекании по нему тока I
внутри соленоида возбуждается однородное поле, индукция которого равна Поток через каждый из витков равен =BS, а полный магнитный поток, сцепленный с соленоидом
где l – длина соленоида (которая предполагается очень большой), S – площадь поперечного сечения, n – число витков на единицу длины (произведение nl дает полное число витков N).
Итак, для индуктивности очень длинного соленоида имеем
где – объем соленоида.
К оглавлению
(19.5)
Слайд 1219.2. Самоиндукция и взаимоиндукция
Рассмотрим явление самоиндукции. Так как поток рассеяния
не влияет на изменение магнитного поля в самом проводнике, то
можно эту величину не учитывать. Рассмотрим первое полученное слагаемое. Если в проводнике i=const, то меняется индуктивность. Для второго слагаемого L=const, а меняется сила тока в проводнике.
Самоиндукция — изменение тока в самом проводнике под действием собственного магнитного поля.
Явление взаимоиндукции состоит в возникновении ЭДС в одной цепи под действием изменения тока в другой.
(19.6)
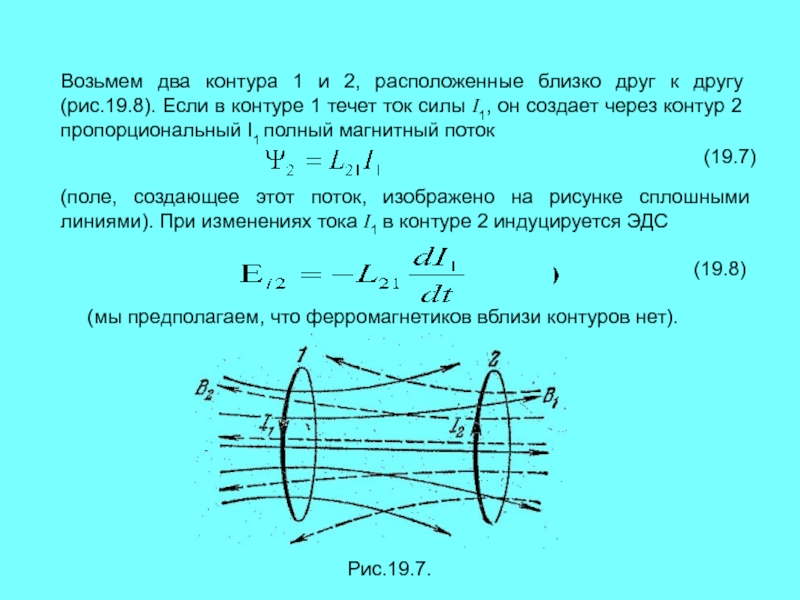
Слайд 13Возьмем два контура 1 и 2, расположенные близко друг к
другу (рис.19.8). Если в контуре 1 течет ток силы I1,
он создает через контур 2 пропорциональный I1 полный магнитный поток(19.7)
(поле, создающее этот поток, изображено на рисунке сплошными линиями). При изменениях тока I1 в контуре 2 индуцируется ЭДС
(мы предполагаем, что ферромагнетиков вблизи контуров нет).
Рис.19.7.
(19.8)
Слайд 14Аналогично, при протекании в контуре 2 тока силы I2 возникает
сцепленный с контуром 1 поток
(поле, создающее этот ток, изображено пунктирными
линиями).При изменениях тока I2 в контуре 1 индуцируется ЭДС
Контуры 1 и 2 называются связанными, а явление возникновения ЭДС в одном из контуров при изменениях силы тока в другом называется взаимной индукцией.
Коэффициенты пропорциональности L12 и L21 называются взаимной индуктивностью контуров. Соответствующий расчет дает, что в отсутствие ферромагнетиков эти коэффициенты всегда равны друг другу:
Их величина зависит от формы, размеров и взаимного расположения контуров, а также магнитной проницаемости окружающей контуры среды. Измеряется L12 в тех же единицах, что и индуктивность L.
К оглавлению
(19.9)
(19.10)
(19.11)
Слайд 1519.3. Энергия и плотность энергии магнитного поля
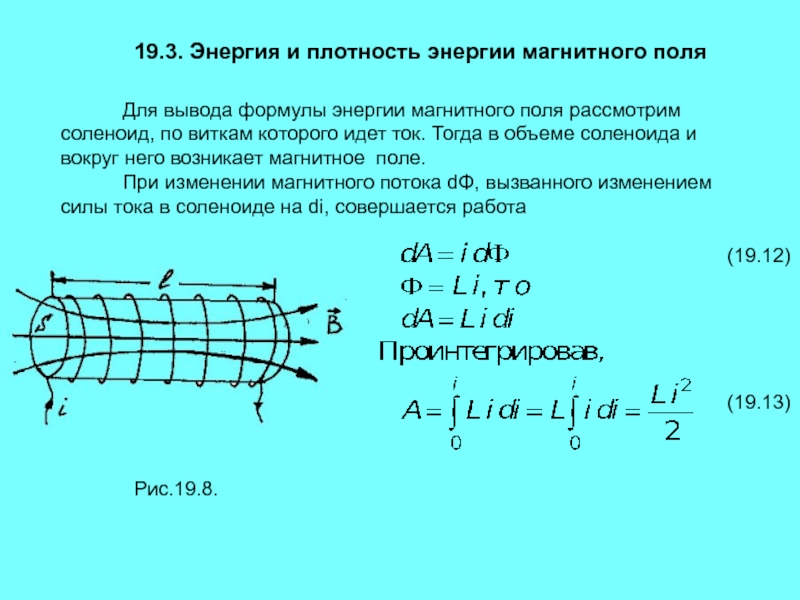
Для вывода
формулы энергии магнитного поля рассмотрим соленоид, по виткам которого идет
ток. Тогда в объеме соленоида и вокруг него возникает магнитное поле.При изменении магнитного потока d, вызванного изменением силы тока в соленоиде на di, совершается работа
Рис.19.8.
(19.13)
(19.12)