Слайд 1Тема 6
6.5.6. Построение теоретического профиля кулачка
После определения
основных размеров кулачкового механизма и выбора законов движения ведомого звена
приступают к основной задаче – проектированию профиля кулачка.
При этом считаются известными закон движения ведомого звена, максимально допустимый угол давления и все размеры, не относящиеся к профилю кулачка.
Задача синтеза, как и задача кинематического анализа кулачковых механизмов, решается методом обращения движения.
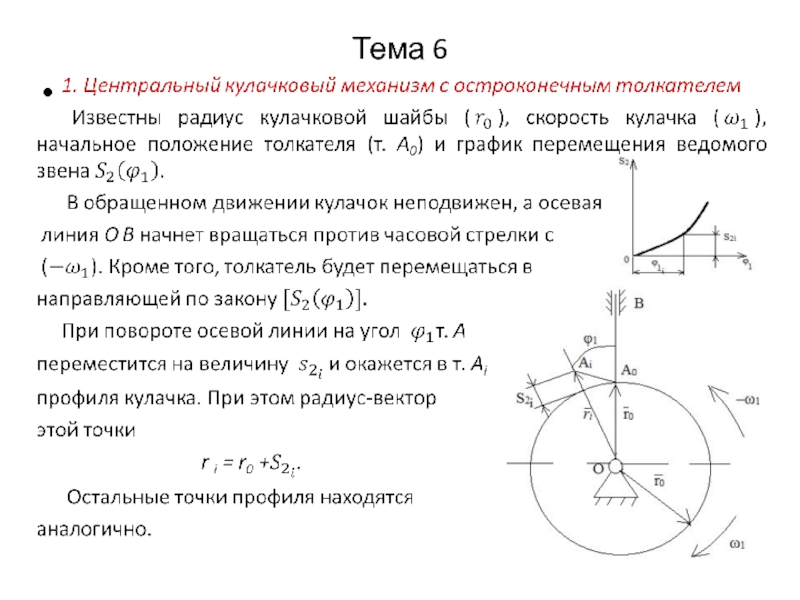
Всему механизму сообщается вращение с угловой скоростью, равной угловой скорости кулачка и направленной в противоположную сторону. В этом случае кулачок как бы останавливается, а ведомое звено будет вращаться вокруг кулачка с угловой скоростью равной – w1 и одновременно перемещаться относительно своих направляющих по заданному закону. Показывая эти перемещения в обращенном движении, отмечаются точки теоретического профиля.
Рассмотрим примеры построения теоретических профилей в различных кулачковых механизмах.
Слайд 6Тема 6
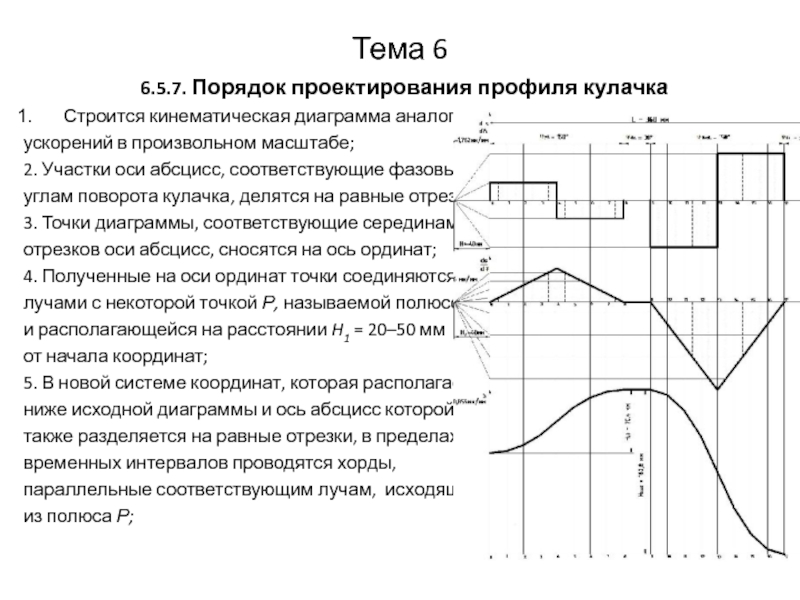
6.5.7. Порядок проектирования профиля кулачка
Строится кинематическая диаграмма аналога
ускорений в
произвольном масштабе;
2. Участки оси абсцисс, соответствующие фазовым
углам поворота кулачка,
делятся на равные отрезки;
3. Точки диаграммы, соответствующие серединам
отрезков оси абсцисс, сносятся на ось ординат;
4. Полученные на оси ординат точки соединяются
лучами с некоторой точкой Р, называемой полюсом
и располагающейся на расстоянии H1 = 20–50 мм
от начала координат;
5. В новой системе координат, которая располагается
ниже исходной диаграммы и ось абсцисс которой
также разделяется на равные отрезки, в пределах
временных интервалов проводятся хорды,
параллельные соответствующим лучам, исходящим
из полюса Р;
Слайд 7Тема 6
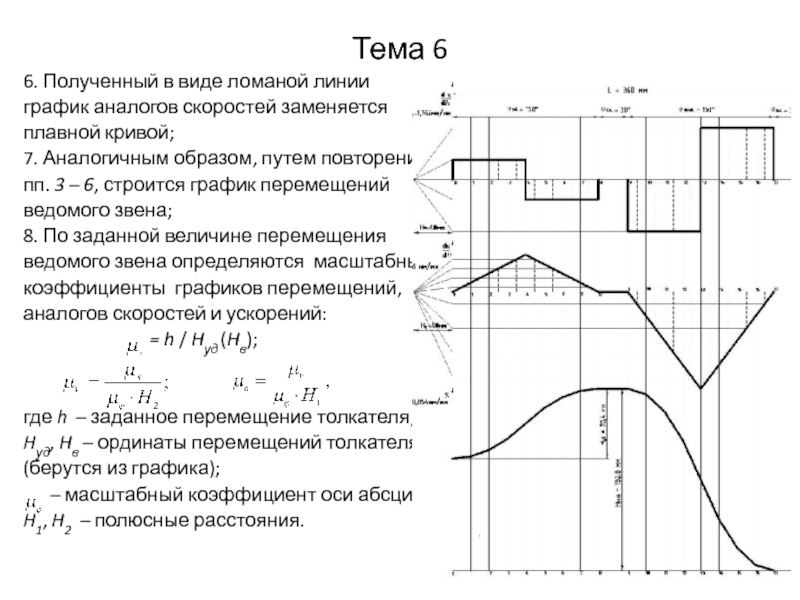
6. Полученный в виде ломаной линии
график аналогов скоростей заменяется
плавной кривой;
7. Аналогичным образом, путем повторения
пп. 3 – 6, строится
график перемещений
ведомого звена;
8. По заданной величине перемещения
ведомого звена определяются масштабные
коэффициенты графиков перемещений,
аналогов скоростей и ускорений:
= h / Hуд (Hв);
где h – заданное перемещение толкателя;
Hуд, Hв – ординаты перемещений толкателя
(берутся из графика);
– масштабный коэффициент оси абсцисс;
H1, H2 – полюсные расстояния.
Слайд 8Тема 6
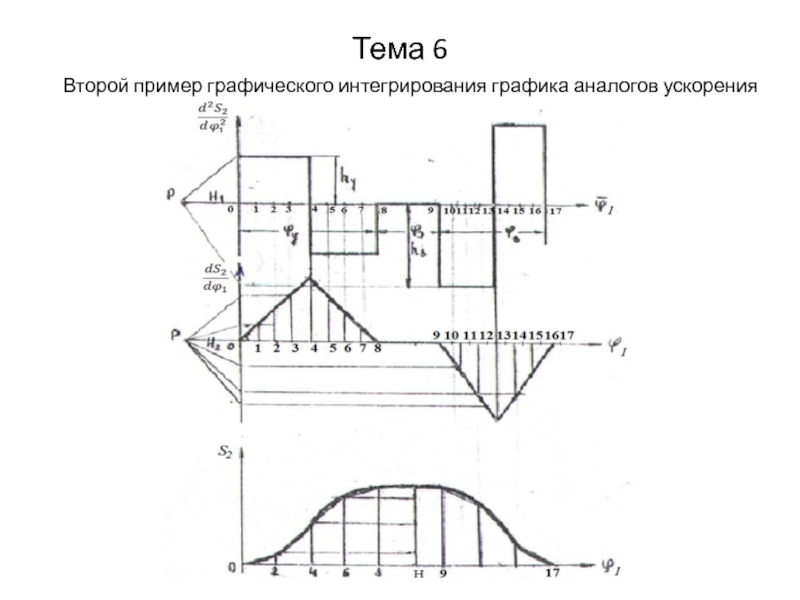
Второй пример графического интегрирования графика аналогов ускорения
Слайд 9Тема 6
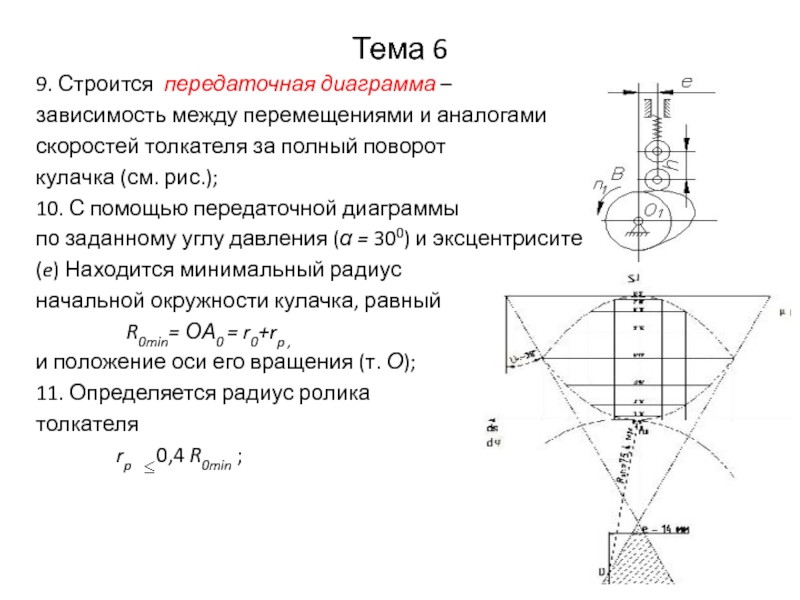
9. Строится передаточная диаграмма –
зависимость между перемещениями и
аналогами
скоростей толкателя за полный поворот
кулачка (см. рис.);
10. С помощью
передаточной диаграммы
по заданному углу давления (α = 300) и эксцентриситету
(e) Находится минимальный радиус
начальной окружности кулачка, равный
R0min= ОА0 = r0+rp ,
и положение оси его вращения (т. О);
11. Определяется радиус ролика
толкателя
rp 0,4 R0min ;
Слайд 10Тема 6
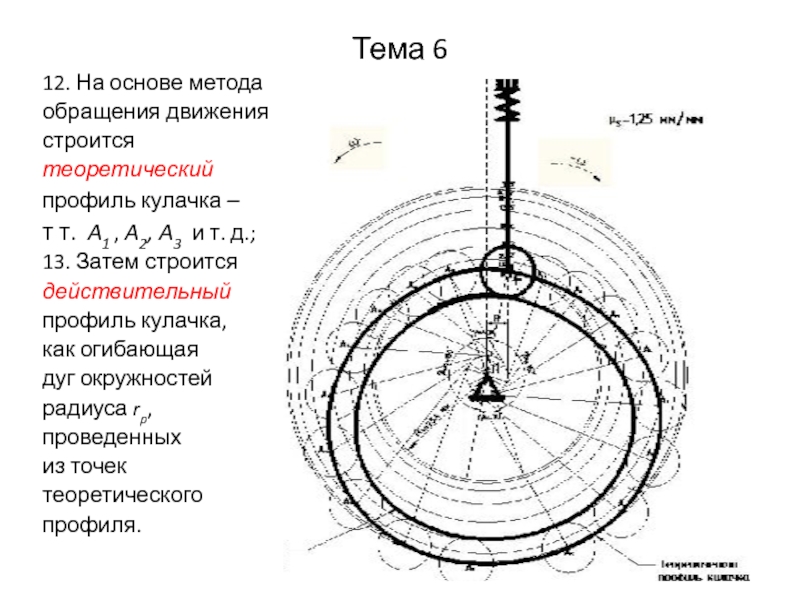
12. На основе метода
обращения движения
строится
теоретический
профиль кулачка –
т т. A1 , A2, A3 и т. д.;
13. Затем
строится
действительный
профиль кулачка,
как огибающая
дуг окружностей
радиуса rp,
проведенных
из точек
теоретического
профиля.
Слайд 11Тема 7
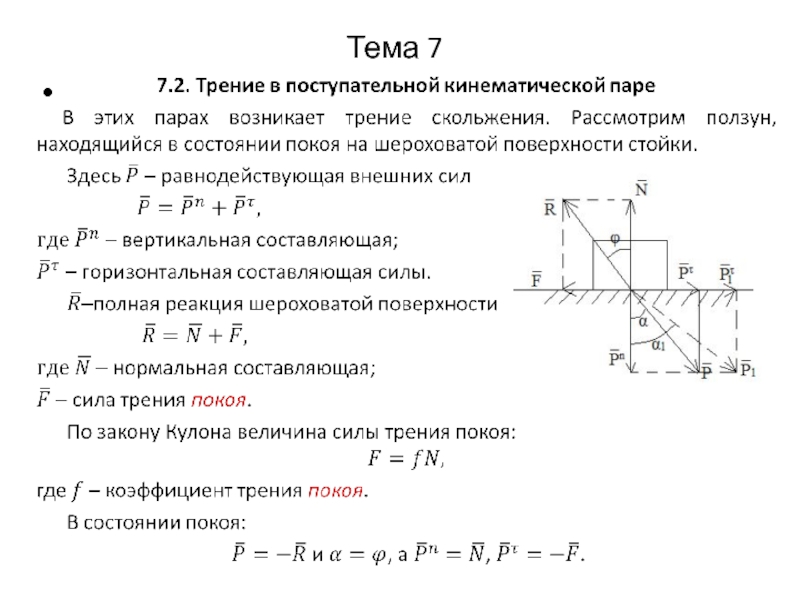
Тема 7. Учет сил трения при силовом анализе
7.1. Виды
трения
При относительном движении звеньев кинематической пары
между соприкасаемыми поверхностями возникает взаимодействие, называемое трением.
Силой трения называется сила противодействия, сопровождающая сопротивление движению.
В большинстве случаев сила трения относится к силам сопротивления, однако в некоторых машинах и механизмах эти силы будут являться движущими (трение используется в ременных и фрикционных передачах, за счет сил трения осуществляется качение в высших КП, вибрационное перемещение, работа домкратов и т. д.).
В зависимости от характера движения звеньев кинематической пары различают следующие виды трения:
– трение скольжения (возникает в низших кинематических парах).
– трение качения (возникает в высших кинематических парах).
Слайд 12Тема 7
Трение скольжения возникает при волочении тела,
т.е. когда оно не вращается вокруг своей оси, а скользит
(трение поршня о цилиндр или вала о цапфу). Трение качения – при движении тела перекатыванием, когда оно вращается вокруг своей оси.
Возникновение трения объясняется тремя причинами:
1. Неровностями соприкасающихся поверхностей, поскольку они не абсолютно гладкие;
2. Силами межмолекулярного воздействия;
3. Деформируемостью соприкасающихся поверхностей.
В зависимости от состояния трущихся поверхностей различают следующие виды трения скольжения:
– сухое трение, при котором происходит непосредственное соприкосновение поверхностей КП;
– жидкостное трение, при котором поверхности разделяются слоем смазки.
Кроме того существуют промежуточные виды трения: полусухое и полужидкостное, в зависимости от того какой вид трения преобладает.
Слайд 24Тема 7
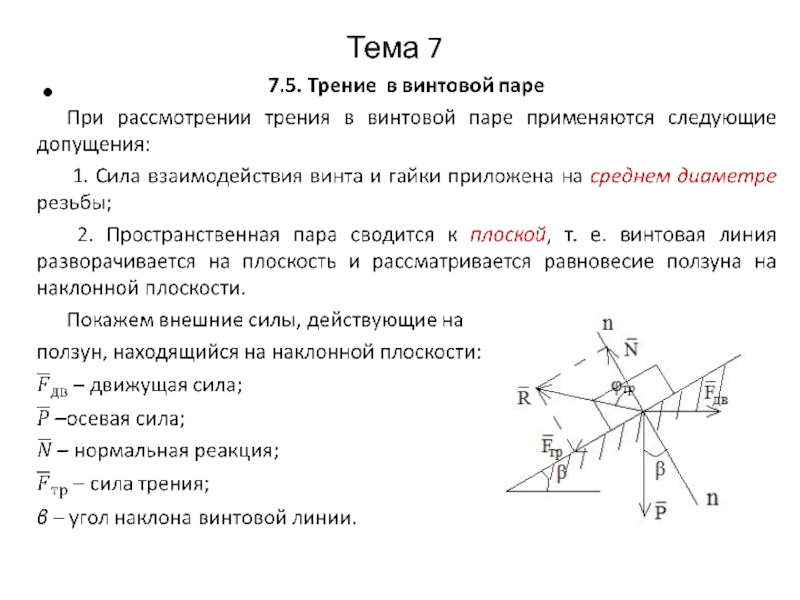
7.6.Теоретические основы вибрационного перемещения
Вибрационное перемещение –
среднее одностороннее направленное движение тел под действием периодических сил. На
рис. показана расчетная схема для определения основных сил, действующих на тело, располагающееся на горизонтальной шероховатой поверхности, вибрирующей под углом α по закону
где s – перемещение; δ – размах колебаний;
– частота колебаний.
Сила инерции Ф определится выражением
Ф = – m . а,
где m – масса тела; а – ускорение движения.
С учетом этого сила инерции будет равна
Силу трения Fтр. найдем, используя закон Кулона:
Fтр. = fтр. .N.
Слайд 25Тема 7
В последнем выражении N – сила
нормального давления, которую определим из уравнения проекций всех сил на
ось y
где g – ускорение свободного падения;
fтр. – коэффициент трения скольжения;
α – угол бросания.
Сила трения в этих выражениях будет переменной по величине и направлению
Эта сила будет являться движущей силой, вызывающей вибрационное перемещение, т.е. проскальзывание тела по шероховатой поверхности либо вперед, либо назад в зависимости от соотношения между силами тяжести и инерции.
Введем горизонтальную амплитуду колебаний
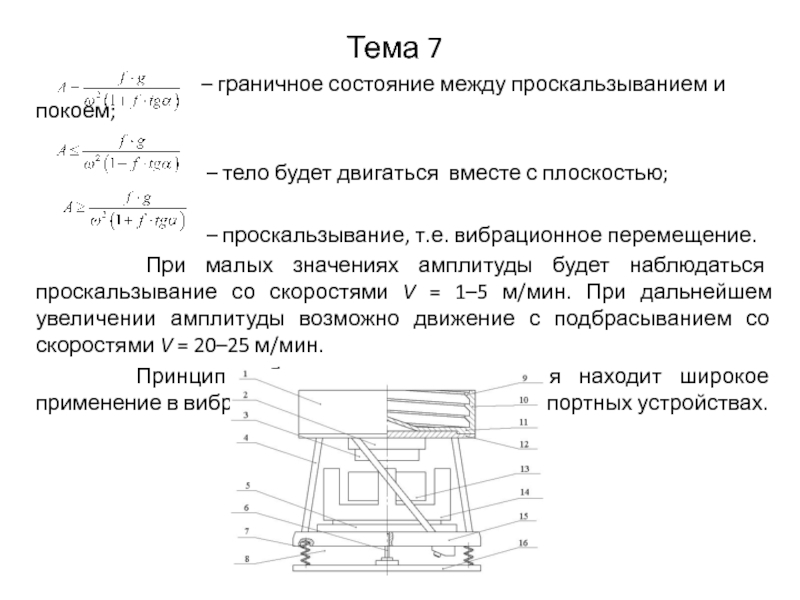
– граничное
состояние между проскальзыванием и покоем;
– тело будет двигаться вместе с плоскостью;
– проскальзывание, т.е. вибрационное перемещение.
При малых значениях амплитуды будет наблюдаться проскальзывание со скоростями V = 1–5 м/мин. При дальнейшем увеличении амплитуды возможно движение с подбрасыванием со скоростями V = 20–25 м/мин.
Принцип вибрационного перемещения находит широкое применение в вибрационных загрузочных и транспортных устройствах.
Слайд 27Тема 7
7.7. Механический КПД механизмов и машин
Коэффициент полезного
действия (КПД) − это безразмерная величина, характеризующая количество полезно используемой
механизмом или машиной суммарной энергии.
В период установившегося движения соблюдается условие равенства работ движущих сил и сил сопротивлений
Адв= Ас.
Работа сил сопротивления складывается из суммы сил полезного сопротивления, т. е. тех сил, для преодоления которых предназначен механизм или машина, и сил вредного сопротивления, к которым относятся силы трения, силы аэрогидродинамического сопротивления и т. д.
Адв= Апс + Атр.
Количественно КПД определяется отношением работы сил полезного сопротивления к работе движущих сил
Выразим работу сил полезного сопротивления
Апс = Адв − Атр.
где коэффициент потерь, который показывает, какая часть работы движущих сил расходуется на преодоление непроизводственных сопротивлений.
Коэффициент полезного действия (КПД) механизма всегда меньше единицы, так как так как коэффициент потерь не может быть равен нулю из-за потерь механической энергии, вызванных наличием трения в кинематических парах
Чем ближе значение КПД к единице, тем меньше потери, следовательно, выше качество механизма или машины.
Каждая машина представляет собой комплекс механизмов, соединенных последовательно или параллельно. Поэтому общий КПД можно вычислить по отдельным ее элементам.
Слайд 29Тема 7
Последовательное соединение механизмов
Рассмотрим машину, состоящую
из последовательно соединенных механизмов, условно обозначенных на схеме цифрами 1,
2 и 3.
Пусть к механизму 1 подводится работа величиной Адв. На выходе получаем работу величиной А1, которая подводится к механизму 2. Таким образом, А1 − работа сил полезного сопротивления 1-го механизма и движущих сил 2-го механизма; А2 − работа сил полезного сопротивления 2-го механизма и движущих сил 3-го механизма; А3 − работа сил полезного сопротивления машины. Величина работы на выходе всегда меньше, чем подведенная работа на входе (А1<Адв, A2
Частные КПД механизмов: =А1/ Адв; =А2/ А1; =А3/ А2.
Общий КПД машины
(1)
Слайд 30Тема 7
Найдем произведение частных
КПД
(2)
Сравнивая (1) и (2), можно сделать вывод, что общий механический КПД машины, состоящей из последовательно соединенных n механизмов, равен произведению их КПД:
2. Параллельное соединение механизмов
Рассмотрим машину, состоящую из трех параллельно соединенных механизмов, условно обозначенных на схеме цифрами 1, 2, 3.
Пусть к механизмам подводится работа
величиной Адв, которая распределяется на
каждый механизм в разных долях,
определяемых коэффициентами а1, а2, а3,
каждый из которых меньше 1, а их сумма
а1 + а2 + а3 = 1.
Слайд 31Тема 7
Общий КПД машины
(3)
Так как
Подставив эти выражения в (3), получим
Отсюда следует, что общий механический КПД машины при параллельном соединении механизмов равен сумме величин КПД каждого механизма, умноженных на коэффициенты долей работ, подводимых к механизмам:
Здесь а1 + а2 + а3 + …. + аn = 1.
Слайд 32Тема 7
Сравним варианты последовательного и параллельного соединения
механизмов с точки зрения минимизации механических потерь в машине. Пусть
величины КПД каждого механизма равны .
При этом коэффициенты, учитывающие доли распределения общей работы Адв между всеми механизмами, также равны:
Тогда
Так как η < 1, то η3 < η. Отсюда следует, что параллельное соединение механизмов в машине предпочтительнее с точки зрения уменьшения механических потерь.