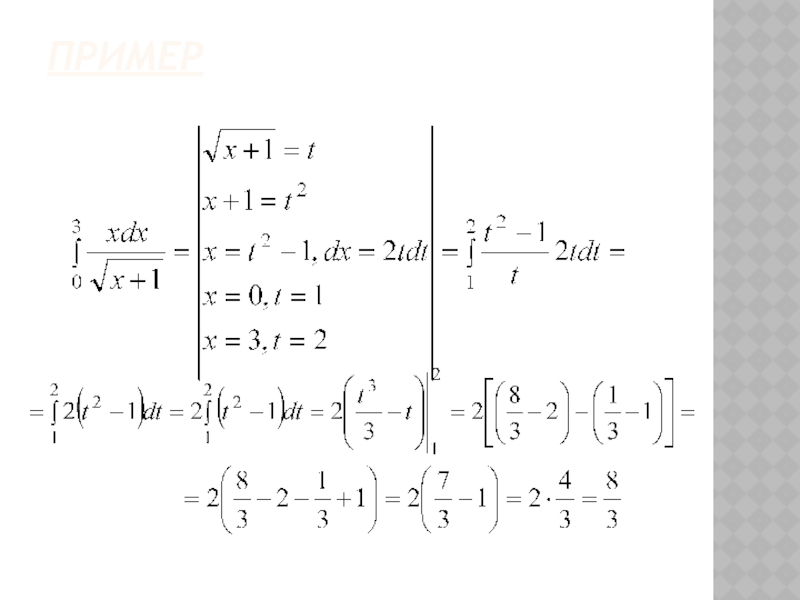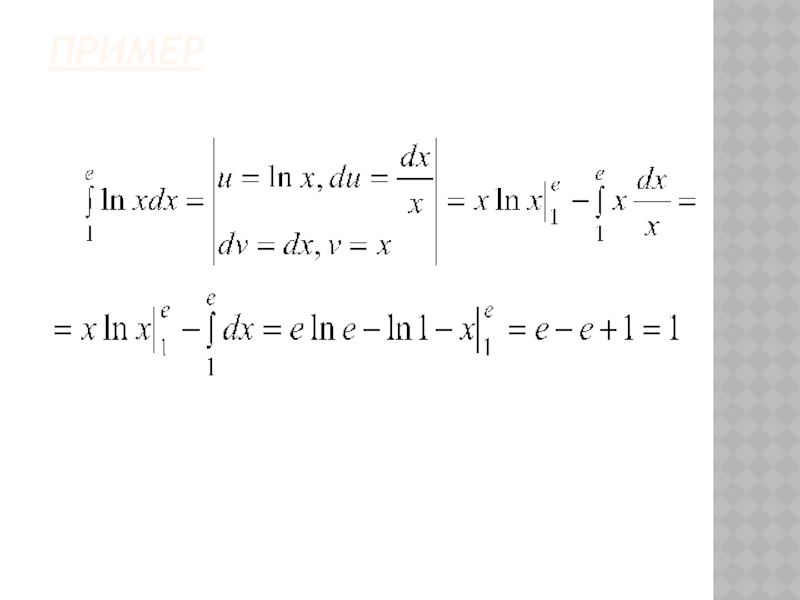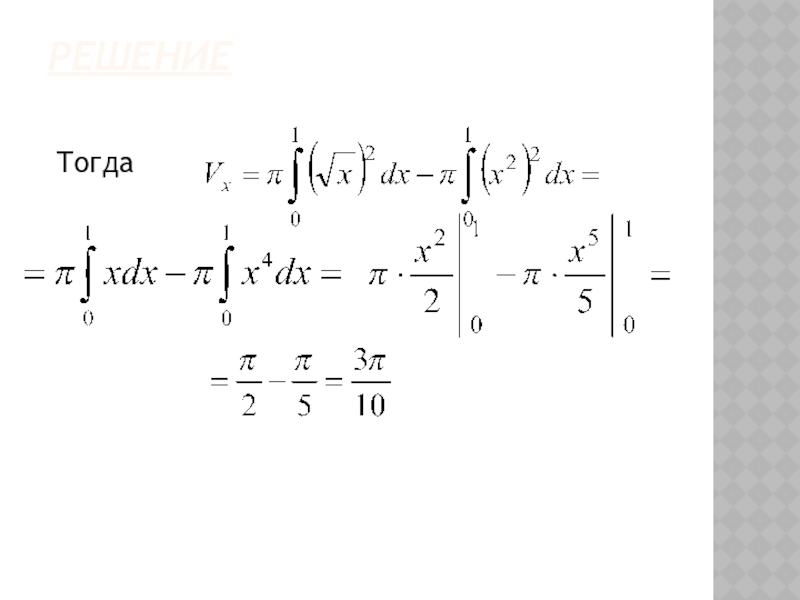Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕМА 8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Содержание
- 1. ТЕМА 8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
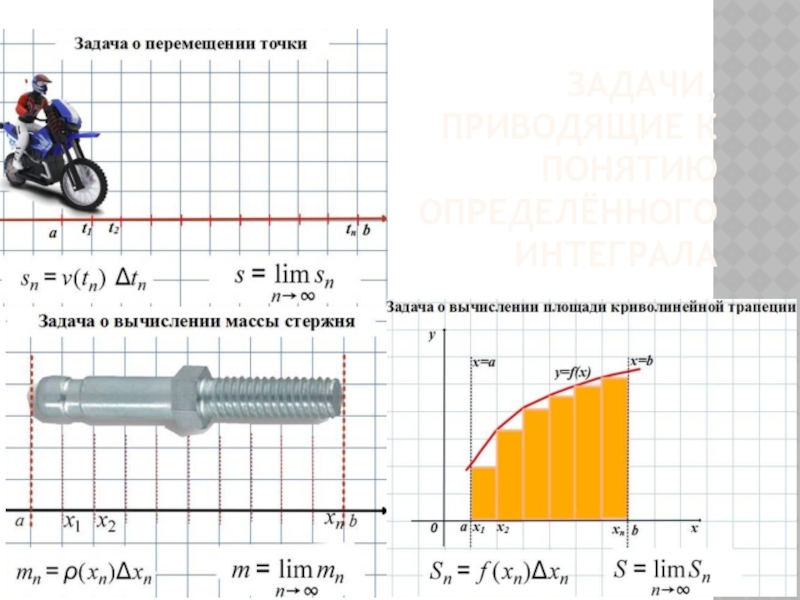
- 2. Задачи, приводящие к понятию определённого интеграла
- 3. Для функции y=f(x) на отрезке [a;b]:Разбить отрезок
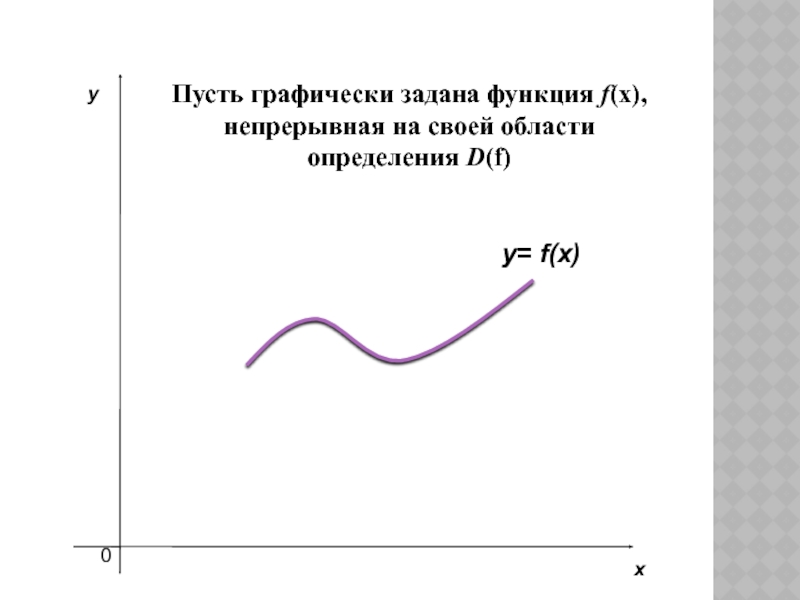
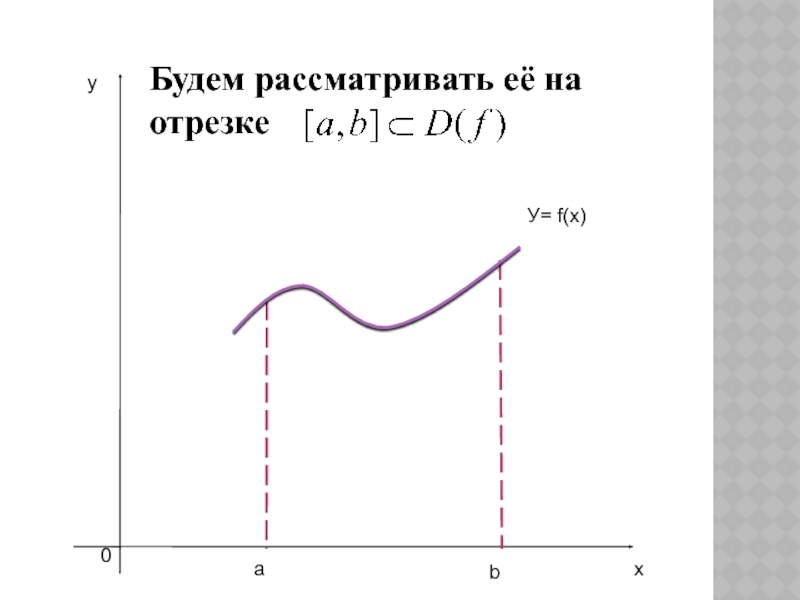
- 4. Пусть графически задана функция f(x), непрерывная на своей области определения D(f)y
- 5. Будем рассматривать её на отрезкеyаb
- 6. Построим фигуру, ограниченную графиком функции y =
- 7. Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a
- 8. Каждой полосе поставим в соответствие прямоугольник, одна
- 9. Основание i-го прямоугольника равно разности xi+1-хi, которую
- 10. Площадь i-го прямоугольника равна:Сложив площади всех прямоугольников, получаем приближенное значение площади S криволинейной трапеции:
- 11. Точное значение площади S получается как предел
- 12. Если предел функции f(x) существует, то f(x)
- 13. Слайд 13
- 14. Определенный интеграл не зависит от выбора первообразной
- 15. Свойства определенного интегралаПусть на отрезке существует определенный интегралгде
- 16. 4. Константу как множитель можно выносить за
- 17. 6. Если подынтегральная функция неотрицательна, то
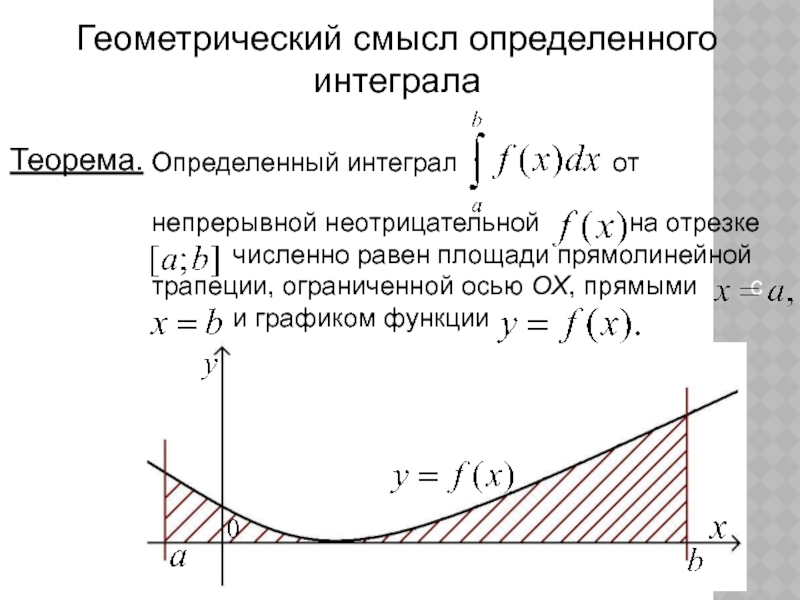
- 18. Геометрический смысл определенного интегралаТеорема.Определенный интеграл
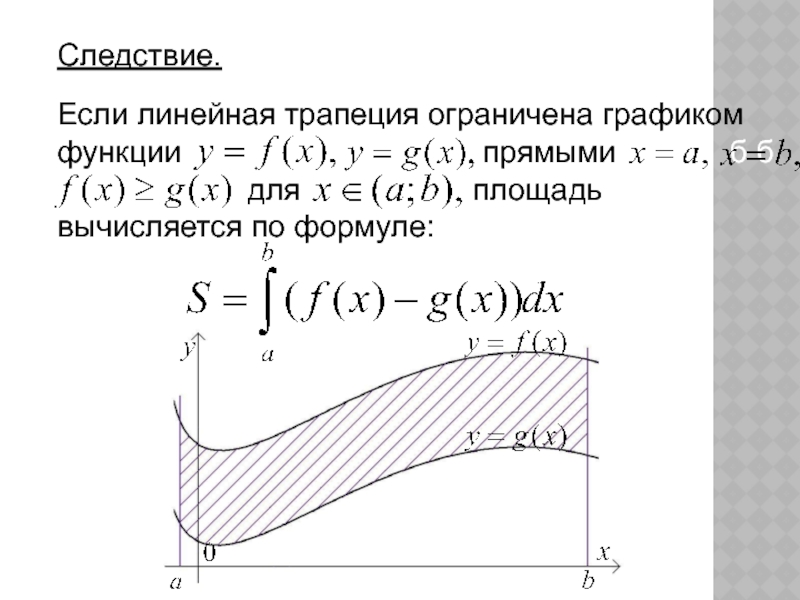
- 19. Следствие.Если линейная трапеция ограничена графиком функции
- 20. Связь и отличие определенных и неопределенных интеграловСвязь:Как
- 21. Отличие:Неопределенный интеграл – общее выражение для всех первообразных, определенный интеграл – это число.
- 22. Теорема о существовании определенного интеграла
- 23. Свойства определенного интеграла
- 24. Свойства определенного интеграла
- 25. Теорема о среднем Если функция непрерывна
- 26. Вычисление определенного интеграла
- 27. Формула Ньютона-Лейбница
- 28. Вычисление определённого интеграла
- 29. Пример Вычислить .
- 30. Вычисление интеграла
- 31. Теорема. Дано: Введем новую переменную, связанную с
- 32. тогда
- 33. Пример
- 34. Слайд 34
- 35. Пример
- 36. Несобственный интеграл
- 37. Пример. Вычислить несобственный интеграл (или установить его расходимость).Этот несобственный интеграл расходится.
- 38. ПримерНесобственный интеграл
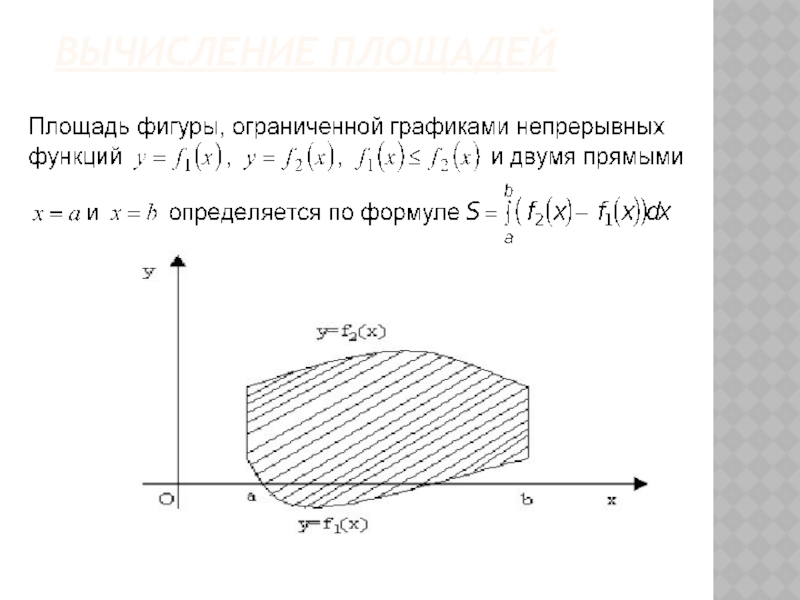
- 39. 1. Вычисление площадей Площадь фигуры в декартовых координатах:Геометрические приложения определенного интеграла
- 40. Вычисление площадей
- 41. Вычисление площадей В случае параметрического задания
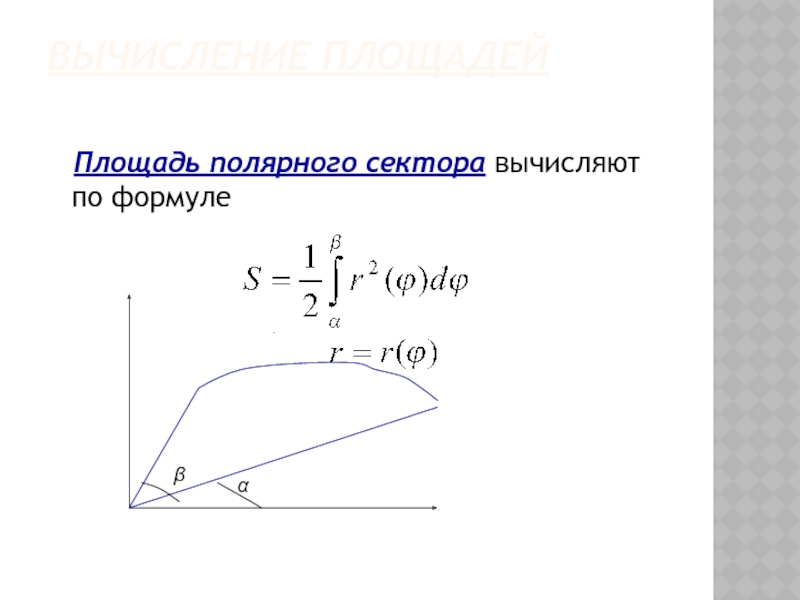
- 42. Вычисление площадей Площадь полярного сектора вычисляют по формуле . α β
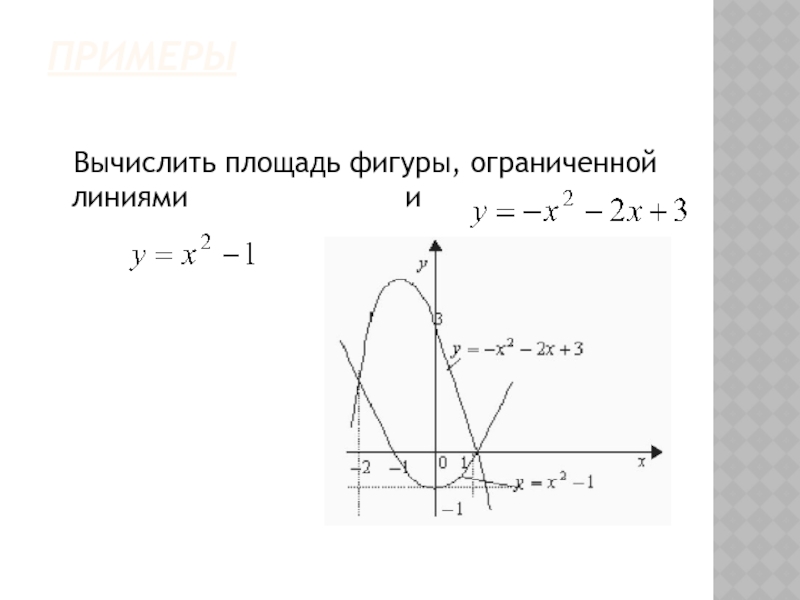
- 43. Примеры Вычислить площадь фигуры, ограниченной линиями
- 44. Продолжение Получим
- 45. Примеры Найти площадь эллипса
- 46. Пример Площадь фигуры, ограниченной
- 47. Вычисление длины дуги Если кривая задана
- 48. Длина дуги в декартовых координатах Если кривая
- 49. Длина дуги в полярных координатах Если
- 50. ПримерыВычислить длину дуги кривой от точки
- 51. Вычисление объема тела вращения. Объем тела,
- 52. Вычисление объема тела вращения Объем тела,
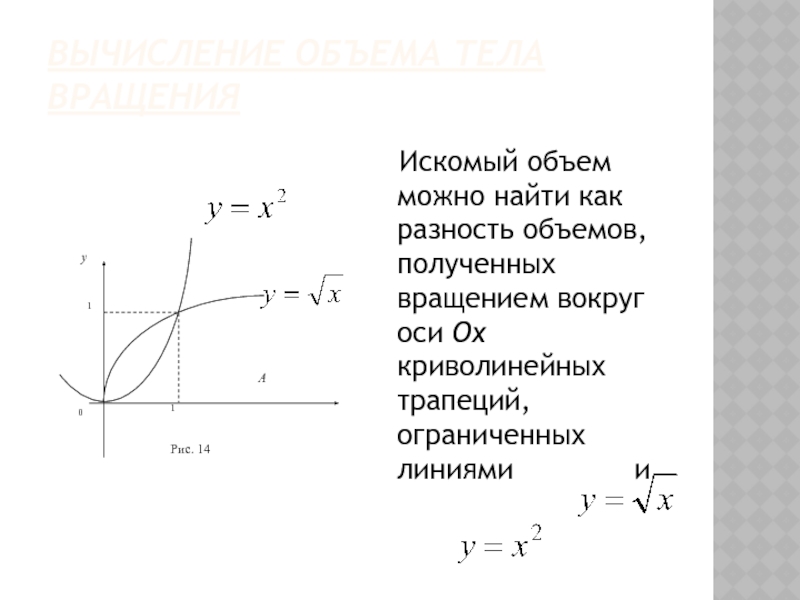
- 53. Вычисление объема тела вращения Искомый объем
- 54. Решение Тогда
- 55. Скачать презентанцию
Задачи, приводящие к понятию определённого интеграла
Слайды и текст этой презентации
![Для функции y=f(x) на отрезке [a;b]:Разбить отрезок [a;b] на n равных частей Составить сумму Sn =f(x0)·∆x0+…+ f(xn)·∆xnВычислить](/img/thumbs/f12914974c52a16e92818bd308455840-800x.jpg "ТЕМА 8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Для функции y=f(x) на отрезке [a;b]:Разбить отрезок [a;b] на n равных")
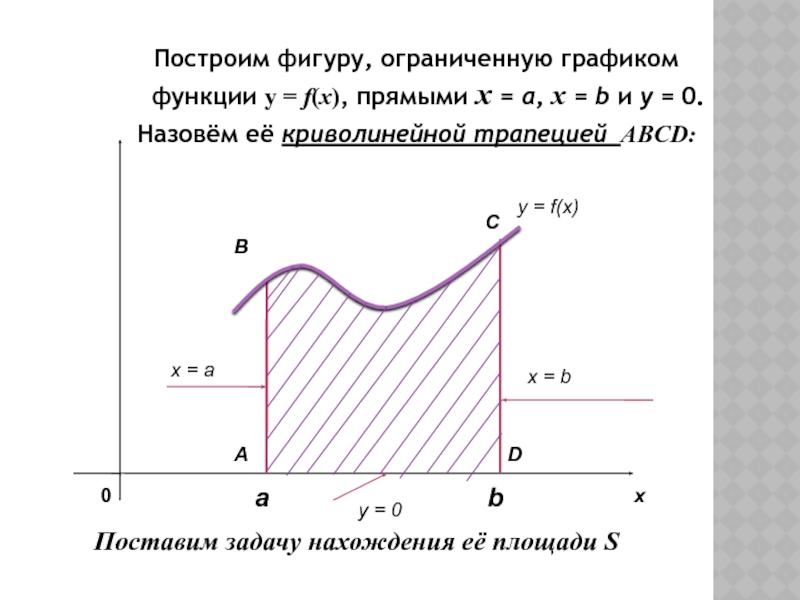
Слайд 6Построим фигуру, ограниченную графиком функции y = f(x), прямыми x
= а, x = b и у = 0.
Назовём
её криволинейной трапецией ABCD:Поставим задачу нахождения её площади S
а
b
x = a
B
C
D
A
x = b
y = 0
Слайд 7Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0=
a
а, у=х1, у = х2, …у = хi, y= xi+1,…, y= b. Этими прямыми трапеция ABCD разбивается на полосы.
x0
xn
![Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a](/img/thumbs/e2580c9fa457884f98aff4ce18570d7d-800x.jpg "ТЕМА 8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a")
Слайд 8Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть
отрезок [xi;xi+1], а смежная сторона – это отрезок f(xi) (i=0…n-1)
y
В
С
А
D
Криволинейная
трапеция заменится некоторой ступенчатой фигурой, составленной из отдельных прямоугольниковx0
xn
![Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть отрезок [xi;xi+1], а смежная сторона – это](/img/thumbs/5ccd415d827375c531378e9a0d516f81-800x.jpg "ТЕМА 8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть отрезок")
Слайд 9Основание i-го прямоугольника равно разности xi+1-хi, которую мы будем обозначать
через Высота i-го прямоугольника равна
f(xi)y
В
С
A
D
x0
xn
Слайд 10Площадь i-го прямоугольника равна:
Сложив площади всех прямоугольников,
получаем приближенное значение
площади S
криволинейной трапеции:
Слайд 11Точное значение площади S получается как предел суммы площадей всех
прямоугольников
Для обозначения предельных сумм вида
f(xi) xi немецкий учёный В.Лейбниц ввёл символ - интеграл функции f(x) от а до b
Слайд 12Если предел функции f(x) существует,
то f(x) называется
интегрируемой на отрезке
[a, b].
Числа а и b называются нижним и верхним
пределом
интегрирования. При постоянных
пределах интегрирования
определённый интеграл
представляет собой определённое число.
![Если предел функции f(x) существует, то f(x) называетсяинтегрируемой на отрезке [a, b].Числа а и b называются нижним](/img/tmb/3/298795/2cfcc41cdadbec1180c32b3a803e2018-800x.jpg "ТЕМА 8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Если предел функции f(x) существует, то f(x) называетсяинтегрируемой на отрезке [a,")
Слайд 14Определенный интеграл не зависит от выбора первообразной для интегрирования функции.
Теорема.
Теорема.
Для
всякой, непрерывной на отрезке функции, существует
соответствующий определенный интеграл.Доказательство основано на теореме Коши, т.е. существует определенный интеграл, значит, существует разность значений первообразной.
Слайд 164. Константу как множитель можно выносить за знак определенного интеграла.
5.
Определенный интеграл от суммы конечного числа непрерывных функций равен сумме
определенных интегралов от этих функций.
Слайд 176. Если подынтегральная функция неотрицательна, то и определенный интеграл
от нее неотрицателен.
7. Теорема о среднем
Если
- непрерывная функция, то определенный интеграл равен:
Слайд 18Геометрический смысл определенного интеграла
Теорема.
Определенный интеграл
от
непрерывной неотрицательной
на отрезке и численно равен площади прямолинейной трапеции, ограниченной осью ОХ, прямыми с и и графиком функции
Слайд 19Следствие.
Если линейная трапеция ограничена графиком функции
прямыми б б б б для площадь вычисляется по формуле:
Слайд 20Связь и отличие определенных и неопределенных интегралов
Связь:
Как в неопределенном, так
и в определенном интеграле нужно находить первообразную для функции
Слайд 21Отличие:
Неопределенный интеграл – общее выражение для всех первообразных, определенный интеграл
– это число.
Слайд 31Теорема. Дано:
Введем новую переменную,
связанную с формулой
b непрерывна на отрезке
при этом
Слайд 37Пример
. Вычислить несобственный интеграл
(или установить его расходимость)
.
Этот несобственный интеграл
расходится.
Слайд 391. Вычисление площадей
Площадь фигуры в декартовых координатах:
Геометрические приложения
определенного интеграла
Слайд 41Вычисление площадей
В случае параметрического задания
кривой, площадь фигуры,
ограниченной
прямыми
, осью Ох и кривой вычисляют по
формуле
где пределы интегрирования определяют из
уравнений .
.
Слайд 47Вычисление длины дуги
Если кривая задана параметрическими уравнениями
,
, то длина ее дуги,
где –значения параметра, соответствующие концам дуги .
Слайд 48Длина дуги в декартовых координатах
Если кривая задана уравнением
,
то
, где a, b–абсциссы начала и конца дуги .Если кривая задана уравнением
, то , где c, d–ординаты начала и конца дуги
Слайд 49Длина дуги в полярных координатах
Если кривая задана уравнением
в полярных координатах ,
то,
где –значения полярного угла, соответствующие концам дуги .
Слайд 51Вычисление объема тела вращения.
Объем тела, образованного вращением вокруг
оси Ox криволинейной трапеции, ограниченной кривой
, отрезком оси абсцисс и прямыми , вычисляется по формуле .
Слайд 52Вычисление объема тела вращения
Объем тела, образованного вращением вокруг
оси Oy фигуры, ограниченной кривой
, отрезком оси ординат и прямыми , вычисляется по формуле.
Слайд 53Вычисление объема тела вращения
Искомый объем можно найти как
разность объемов, полученных вращением вокруг оси Ox криволинейных трапеций, ограниченных
линиями и
