Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема лекции № 1: Производная и её применение
Содержание
- 1. Тема лекции № 1: Производная и её применение
- 2. «Нет ни одной области математики, как
- 3. Цели занятия:узнать историю открытия производной; узнать основные
- 4. немного из истории Производная –
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Приращение аргумента, приращение функции.Пусть х –
- 11. Слайд 11
- 12. Основные правила дифференцированияЕсли функции u и v
- 13. Таблица производных элементарных функций
- 14. Образцы решения задач.Решая примеры, проговаривайте вслух. Помните: «Мысль рождается с собственной речи!»
- 15. Тест по теме «Производная функции»
- 16. 1. Выражение вида f появилось уже в
- 17. Геометрический смысл производной Геометрический смысл производной со-стоит
- 18. Слайд 18
- 19. Уравнение касательной y = f / (x0)
- 20. Найдите угловой коэффициент касательной к кривой
- 21. Алгоритм нахождения уравнения касательной к графику функции
- 22. к графику функции
- 23. Механический смысл производной (физический смысл производной)
- 24. РЕШАЕМ ЗАДАЧИ! Точка движется по закону а)
- 25. а) V(t) = - t 2 +
- 26. Материальная точка движется прямолинейно по закону x(t)
- 27. Решение.V(t) = x′(t) = 3 t 2
- 28. Ответим на следующие вопросы:Сформулируйте определение производной функции?Как
- 29. “Ум заключается не только в знании, но и в умении применять знания на практике” Аристотель
- 30. Скачать презентанцию
«Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям действительного мира»Н.И. Лобачевский
Слайды и текст этой презентации
Слайд 2«Нет ни одной области математики, как бы абстрактна она ни
была, которая когда-нибудь не окажется применимой к явлениям действительного мира»
Лобачевский
Слайд 3Цели занятия:
узнать историю открытия производной;
узнать основные направления применения производной
в разных областях науки и техники.
ввести определение производной
познакомиться
с правилами дифференцированияУзнать в чём заключается геометрический и физический смысл производной
Слайд 4немного из истории
Производная – одно из фундаментальных
понятий математики, характеризующее скорость изменения функции в данной точке.
Понятие производной возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: определение скорости прямолинейного движения и построения касательной к кривой. Независимо друг от друга Исаак Ньютон и Готфрид Лейбниц разработали теорию дифференциального исчисления.
Слайд 10Приращение аргумента,
приращение функции.
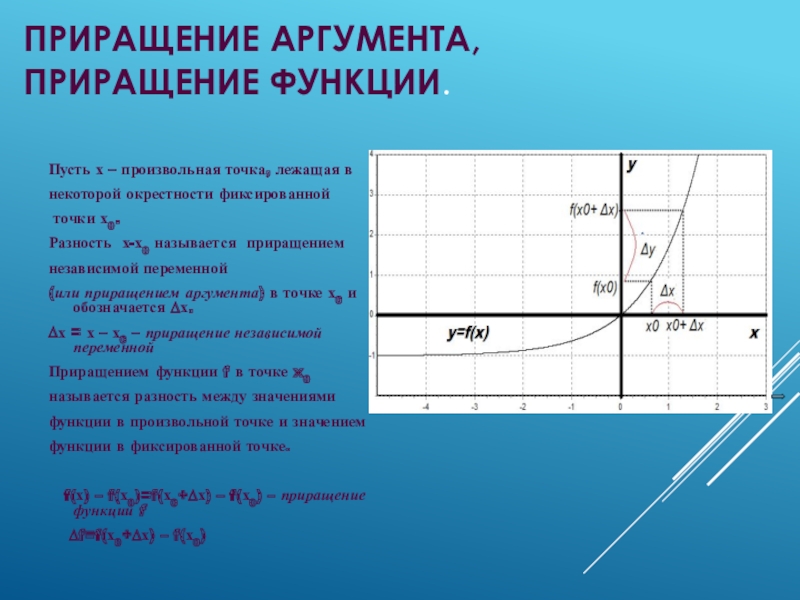
Пусть х – произвольная точка, лежащая в
некоторой окрестности фиксированной
точки х0.
Разность х-х0 называется приращением
независимой
переменной(или приращением аргумента) в точке х0 и обозначается ∆х.
∆х = х – х0 – приращение независимой переменной
Приращением функции f в точке x0
называется разность между значениями
функции в произвольной точке и значением
функции в фиксированной точке.
f(х) – f(х0)=f(х0+∆х) – f(х0) – приращение функции f
∆f=f(х0+∆х) – f(х0)
Слайд 12Основные правила дифференцирования
Если функции u и v дифференцируемы в точке
х0, то справедливы следующие правила:
1. Производная суммы (u+v)'= u' +
v'2. О постоянном множителе (Cu)'=Cu'
3. Производная произведения
(uv)'=u'v+uv'
4. Производная дроби (u/v)'=(u'v-uv') / v2
Слайд 14Образцы решения задач.
Решая примеры, проговаривайте вслух.
Помните: «Мысль рождается с
собственной речи!»
Слайд 16
1. Выражение вида f появилось уже в конце 17 в.
и означает «приращение».
2. Термин производная ввел
в 1797г. Ж. Лагранж3. И. Ньютон называл производную функцию
флюксией , а саму функцию – флюентой.
Раздел математики, в котором изучаются
производные и их применения к исследованию
функций , называется
дифференциальным исчислением.
Дифференциальное исчисление создано
Ньютоном и Лейбницем в конце 17 столетия.
Слайд 17Геометрический смысл производной
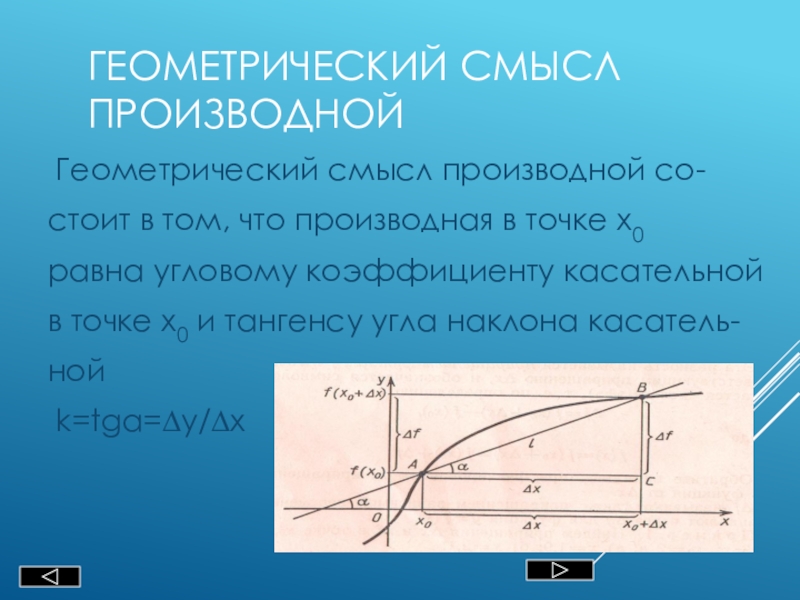
Геометрический смысл производной со-
стоит в том, что
производная в точке х0
равна угловому коэффициенту касательной
в точке х0
и тангенсу угла наклона касатель-ной
k=tgα=∆y/∆x
Слайд 19Уравнение касательной
y = f / (x0) · (x - x0)
+ f(x0)
(x0; f(x0)) – координаты точки касания
f´(x0) = tgα
=k – тангенс угла наклона касательной в данной точке или угловой коэффициент(х;у) – координаты любой точки касательной
Слайд 21Алгоритм нахождения уравнения касательной к графику функции y=f(x).
Вычислим
.
Найдем
Вычислим
Подставим найденные числа a , в формулу
Слайд 23Механический смысл производной
(физический смысл производной)
Механический смысл производной состоит
в том, что производная пути по времени равна мгновенной скорости
в момент времени t0:S'(t0)=V(t0).
Слайд 24РЕШАЕМ ЗАДАЧИ!
Точка движется по закону
а) выведите формулу для вычисления
скорости движения
точки в любой момент времени t
( t > 0);б) найдите скорость в момент t = 2c;
в) через сколько секунд после начала
движения точка остановится?
Слайд 25а) V(t) = - t 2 + 4 t +
5.
б) V(2) = - 2 2 + 4∙2 + 5
= - 4 + 8 + 5 = 9(м/с).в) V(t) = 0, - t 2 + 4 t + 5 = 0,
t1 = -1,
t2 = 5,
-1 < 0, не удовлетворяет условию задачи.
Точка остановится через 5 секунд после начала движения.
Слайд 26Материальная точка движется прямолинейно по закону x(t) = t 3
– 4 t 2 Перемещение измеряется в метрах.
Найдите:
скорость в момент
t = 5c;ускорение в момент t = 5c.
Слайд 27Решение.
V(t) = x′(t) = 3 t 2 - 8 t
;
V(5) = 3 ∙ 5 2
– 8 ∙ 5 = 35 (м/с).a(t) = x′′(t) = 6t – 8;
a(5) = 6 ∙ 5 – 8 = 22 (м/с 2).
Слайд 28Ответим на следующие вопросы:
Сформулируйте определение производной функции?
Как называется математическая операция
нахождения производной функции?
В чем заключается геометрический смысл производной функции?
Каков физический
(механический) смысл производной?
