Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема лекции №7
Содержание
- 1. Тема лекции №7
- 2. Цель лекции - изучить особенности авторегрессионого моделированияПлан
- 3. 1. Авторегрессонная модель и её видыАвторегрессионная (AR-) модель — модель
- 4. Общий вид модели авторегрессии:Yi = a0 + Ʃai*Yi-1+Ɛiгде a0 — постоянная
- 5. Виды моделейАвторегрессия первого порядка (AR I -
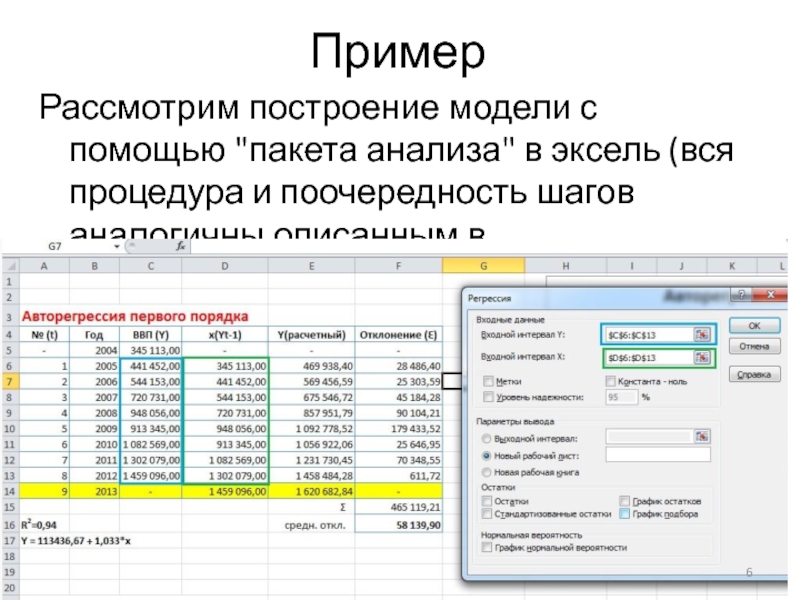
- 6. ПримерРассмотрим построение модели с помощью "пакета анализа"
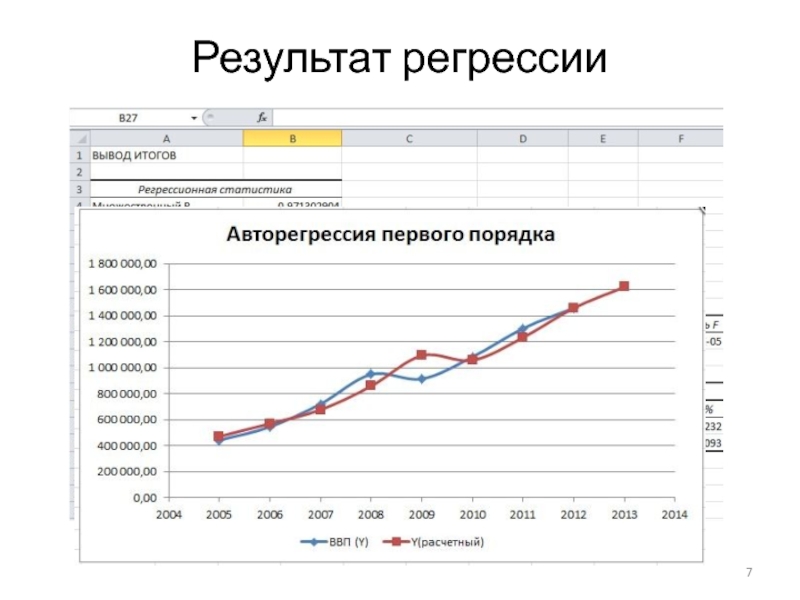
- 7. Результат регрессии
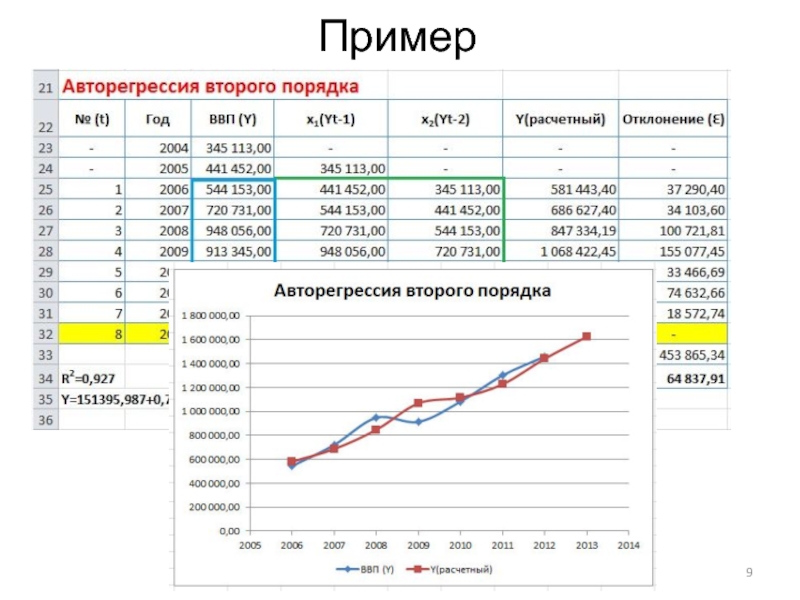
- 8. Авторегрессия второго порядка (AR II -)Yi =
- 9. Пример
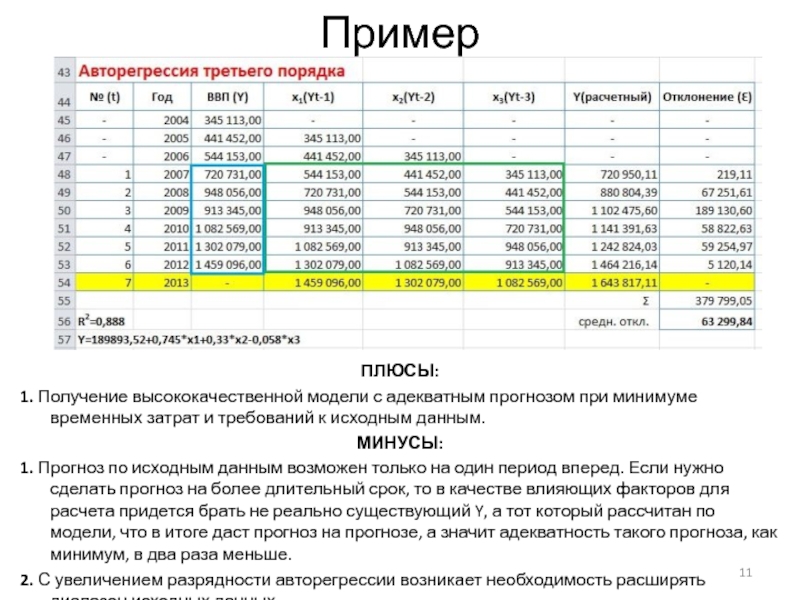
- 10. Авторегрессия третьего порядка (AR III - )Yi =
- 11. ПримерПЛЮСЫ:1. Получение высококачественной модели с адекватным прогнозом при
- 12. 2. Операторное представлениеЕсли ввести лаговый оператор L: LYt=Yt-1
- 13. Стационарность авторегрессионного процесса зависит от корней характеристического
- 14. 3. Автокорреляционная функцияАвтоковариационная и автокорреляционная функции AR(p)-процесса
- 15. В общем случае выражение для математического ожидания
- 16. Скачать презентанцию
Цель лекции - изучить особенности авторегрессионого моделированияПлан лекции.1. Авторегрессонная модель и её виды2. Операторное представление3. Автокорреляционная функция
Слайды и текст этой презентации
Слайд 2Цель лекции - изучить особенности авторегрессионого моделирования
План лекции.
1. Авторегрессонная модель
и её виды
Слайд 31. Авторегрессонная модель и её виды
Авторегрессионная (AR-) модель — модель временных рядов, в
которой значения временного ряда в данный момент линейно зависят от
предыдущих значений этого же ряда.Слайд 4Общий вид модели авторегрессии:
Yi = a0 + Ʃai*Yi-1+Ɛi
где a0 — постоянная - коэффициент описывающий
ситуацию прохождение влияющих факторов через начало координат, то есть показывает
каким будет итог модели в случае, когда влияющие факторы равны нулю;ai — коэффициенты, которые описывают степень зависимости итогового Y от влияющих факторов, в данном случае, от того каким был Y в прошлом периоде регрессии;
Yi-1 — влияющие факторы, которые в данном случае и есть итоговый Y, но тот, каким он был раньше;
Ɛi — случайная компонента или как еще ее принято называть погрешность модели (по сути, это разница между расчетным значением модели за известные периоды и между самими известными значениями, то есть Yрасч. - Y).
Слайд 5Виды моделей
Авторегрессия первого порядка (AR I - )
Yi = a0 + ai*Yi-1+Ɛi
Линейная
модель авторегрессии первого порядка состоит только из одного влияющего фактора,
а именно из Y-1, то есть изучается наиболее тесная зависимость только от того каким был итоговый показатель периодом с шагом назад.Слайд 6Пример
Рассмотрим построение модели с помощью "пакета анализа" в эксель (вся
процедура и поочередность шагов аналогичны описанным в статье Линейная регрессия в
Excel через Анализ данных) на примере ряда динамики ВВП Украины с 2004 по 2012 гг.Слайд 8 Авторегрессия второго порядка (AR II -)
Yi = a0 + ai*Yi-1 + ai*Yi-2 +Ɛi
Модель
авторегрессии второго порядка отличается от первой тем, что она включает
в себя еще один влияющий фактор Yi-2, то есть показывается зависимость от того каким был Y не только один период назад, но и от того каким он был два периода назад. Порой это позволяет выявить большую взаимосвязь и соответственно построить более точный прогноз.Слайд 10Авторегрессия третьего порядка (AR III - )
Yi = a0 + ai*Yi-1 + ai*Yi-2 +
ai*Yi-3 +Ɛi
Модель авторегрессии третьего порядка наиболее тесно описывает зависимость от того
каким был итоговый показатель раньше, так как в качестве влияющих факторов используется три отправные точки - каким Y был 1 период назад, 2 периода назад и 3 периода назад. Требования к размаху исследуемого динамического ряда у этой модели выше - так как диапазон исходных данных сокращается на три периода, то чтобы не пострадало качество модели, необходимо расширять исследуемый период.
Слайд 11Пример
ПЛЮСЫ:
1. Получение высококачественной модели с адекватным прогнозом при минимуме временных затрат
и требований к исходным данным.
МИНУСЫ:
1. Прогноз по исходным данным возможен только
на один период вперед. Если нужно сделать прогноз на более длительный срок, то в качестве влияющих факторов для расчета придется брать не реально существующий Y, а тот который рассчитан по модели, что в итоге даст прогноз на прогнозе, а значит адекватность такого прогноза, как минимум, в два раза меньше.2. С увеличением разрядности авторегрессии возникает необходимость расширять диапазон исходных данных.
Слайд 122. Операторное представление
Если ввести лаговый оператор L: LYt=Yt-1 то авторегрессионную модель
можно представить следующим образом
или
Ла́говый оператор — оператор смещения, позволяющий получить значения элементов временного
ряда на основании ряда предыдущих значений.Слайд 13Стационарность авторегрессионного процесса зависит от корней характеристического полинома
Для того чтобы
процесс был стационарным, достаточно, чтобы все корни характеристического полинома лежали вне
единичного круга в комплексной плоскости |z|>1.В частности, для AR I - процесса a(z)=1-rz, следовательно корень этого «полинома» z=1/r, поэтому условие стационарности можно записать в виде |r|<1, то есть коэффициент авторегрессии (он же в данном случае коэффициент автокорреляции) должен быть строго меньше 1 по модулю.
Для AR(2)-процесса можно показать, что условия стационарности имеют вид: |a2|<1, a2 ±a1<1.
Слайд 143. Автокорреляционная функция
Автоковариационная и автокорреляционная функции AR(p)-процесса удовлетворяют рекуррентным соотношениям:
или
В
простейшем случае AR(1)-процесса, математическое ожидание равно
а дисперсия
Слайд 15В общем случае выражение для математического ожидания через параметры модели
было указано выше, однако, выражение для дисперсии временного ряда -
существенно усложняется. Можно показать, что дисперсия ряда γ(0) и вектор автокорреляций γвыражаются через параметры следующим образом:
где а - вектор параметров,
С - матрица порядка р , элементы которой определяются следующим образом. Диагональные элементы равны cii=1-a2i. Элементы выше диагонали равны –a2i+j-1, а элементы ниже диагонали равны –(aj+a2i-j). Здесь подразумевается, что если индекс превышает порядок модели p, то соответствующая величина приравнивается к нулю.