Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема №3 Задача 1 Задача 4 Задача 2 Задача 3 Задача 5 Задача 6 Задача 7 Задача
Содержание
- 1. Тема №3 Задача 1 Задача 4 Задача 2 Задача 3 Задача 5 Задача 6 Задача 7 Задача
- 2. ЭлектроемкостьПотенциал уединенного проводника и его заряд связаны
- 3. Энергия уединенного заряженного проводника может быть найдена
- 4. Площадь пластин плоского воздушного конденсатора S=1м2, расстояние между ними Найти емкость С этого конденсатора.Задача 1
- 5. Задача 1Дано:С – ? Полное напряжениегде d
- 6. Задача 2Конденсатор предыдущей задачи заряжен до разности потенциалов U=300В. Найти поверхностную плотность заряда на его пластинах.
- 7. Задача 2Дано:- ?Решение:Полная разность потенциалов U0 между
- 8. Задача 3Площадь пластин плоского воздушного конденсатора
- 9. Задача 3Дано:Решение:=1 S -q
- 10. Задача 4Между пластинами плоского конденсатора, находящимися на
- 11. Задача 4Дано:U2 – ? +q-qd0
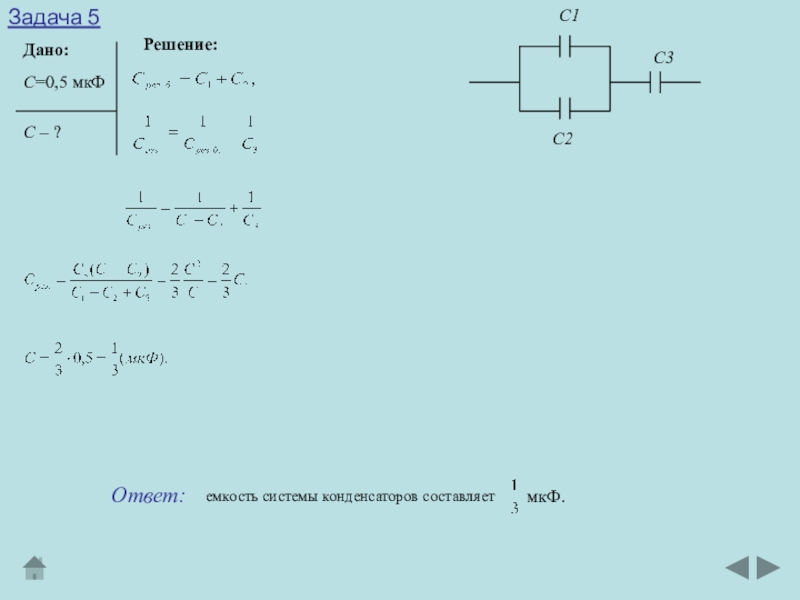
- 12. Найти емкость С системы конденсаторов, изображенной на рисунке. Емкость каждого конденсатора С=0,5 мкФ.Задача 5
- 13. Задача 5С=0,5 мкФС – ?Дано:Решение:C1 C2 C3 емкость системы конденсаторов составляет мкФ. Ответ:
- 14. При помощи электрометра сравнивали
- 15. U1 = 300 ВU2 = 100 ВU
- 16. Задача 7Пластины плоского конденсатора площадью
- 17. Дано:Задача 7Решение:(1)(2)Подставим (2) в (1) и выразим
- 18. Плоский конденсатор заполнен диэлектриком, и на его
- 19. Дано:Задача 8-q+qU-q+q’UПодставим (3), (4), (1) в выражение,
- 20. Скачать презентанцию
ЭлектроемкостьПотенциал уединенного проводника и его заряд связаны соотношениемгде С – емкость уединенного проводника.Емкость плоского конденсаторагде S – площадь каждой пластины конденсатора,d – расстояние между пластинами.Емкость сферического конденсаторагде r и R –
Слайды и текст этой презентации
Слайд 1Тема №3
Задача 1
Задача 4
Задача 2
Задача 3
Задача 5
Задача 6
Задача 7
Задача 8
Электроемкость
Теоретическое
введение
Слайд 2Электроемкость
Потенциал уединенного проводника и его заряд связаны соотношением
где С –
емкость уединенного проводника.
Емкость плоского конденсатора
где S – площадь каждой пластины
конденсатора,d – расстояние между пластинами.
Емкость сферического конденсатора
где r и R – радиусы внутренней и внешней сфер. В частном случае, когда R=,
- емкость уединенного шара.
Емкость цилиндрического конденсатора
где L – высота коаксиальных цилиндров,
r и R – радиусы внутреннего и внешнего цилиндров.
Емкость системы конденсаторов:
при параллельном соединении конденсаторов,
при последовательном соединении конденсаторов.
Слайд 3Энергия уединенного заряженного проводника может быть найдена по одной из
следующих формул
В случае плоского конденсатора энергия
где S – площадь каждой
пластины конденсатора, – поверхностная плотность заряда на пластинах,
U – разность потенциалов между пластинами,
d – расстояние между ними.
Величина
называется объемной плотностью энергии.
Сила притяжения между пластинами плоского конденсатора
Слайд 4Площадь пластин плоского воздушного конденсатора S=1м2, расстояние между ними
Найти емкость С этого конденсатора.
Задача 1
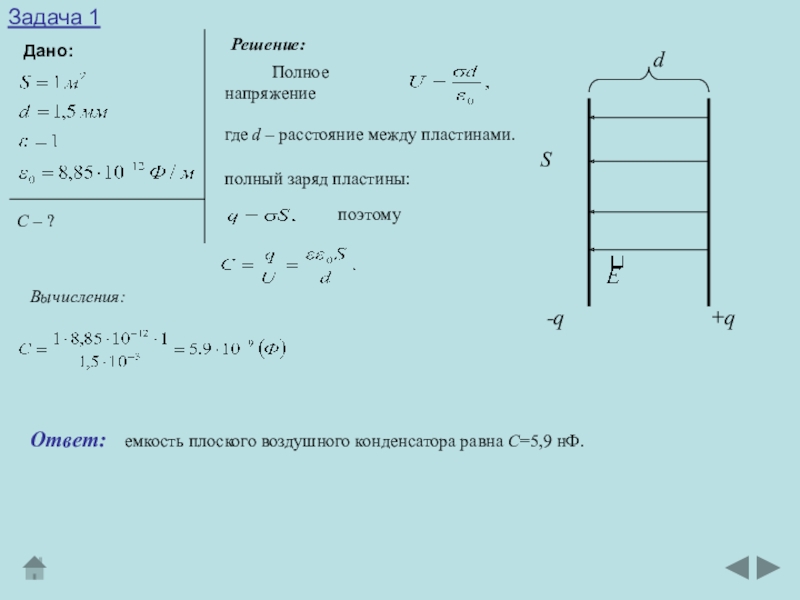
Слайд 5Задача 1
Дано:
С – ?
Полное напряжение
где d – расстояние между
пластинами.
полный заряд пластины:
d
S
-q
+q
Вычисления:
емкость плоского воздушного конденсатора равна С=5,9 нФ.
Ответ:
Решение:
поэтому
Слайд 6Задача 2
Конденсатор предыдущей задачи заряжен до разности потенциалов U=300В. Найти
поверхностную плотность заряда на его пластинах.
Слайд 7Задача 2
Дано:
- ?
Решение:
Полная разность потенциалов U0 между электродами равна
Вычисления:
поверхностная плотность
заряда на пластинах конденсатора
Напряженность поля в плоском конденсаторе выражается
формулой Ответ:
d
S
-q
+q
Слайд 8Задача 3
Площадь пластин плоского воздушного конденсатора
, расстояние между
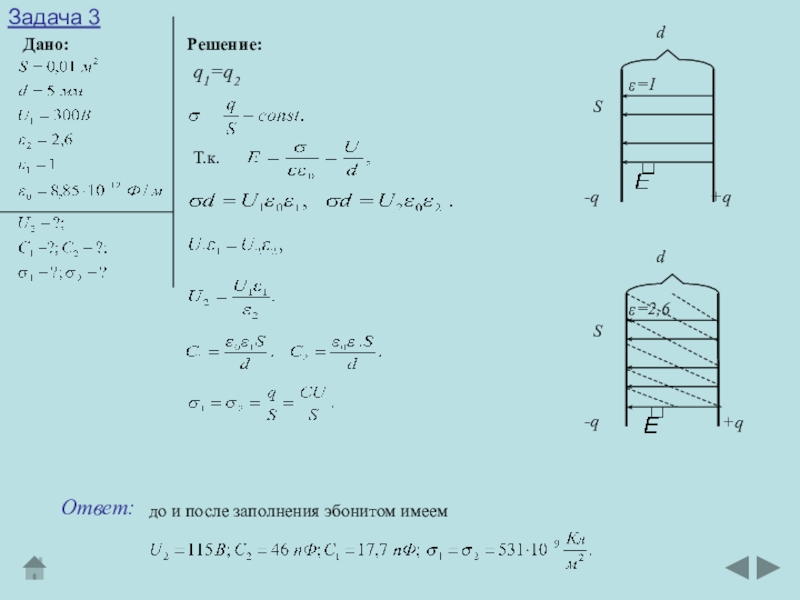
ними d=5 мм. К пластинам конденсатора приложена разность потенциалов . После отключения конденсатора от источника напряжения пространство между пластинами конденсатора заполняется эбонитом. Какова будет разность потенциалов между пластинами после заполнения? Найти емкости конденсатора и поверхностные плотности заряда на пластинах до и после заполнения.
Слайд 9Задача 3
Дано:
Решение:
=1
S
-q
+q
d
=2,6
S
-q
+q
d
Т.к.
до и после заполнения эбонитом имеем
Ответ:
q1=q2
Слайд 10Задача 4
Между пластинами плоского конденсатора, находящимися на расстоянии d=1 см
друг от друга, приложена разность потенциалов U=100 В. К одной
из пластин прилегает плоскопараллельная пластинка кристаллического бромистого таллия ( ) толщиной . После отключения конденсатора от источника напряжения пластинку кристалла вынимают. Какова будет после этого разность потенциалов между пластинами конденсатора?
Слайд 11Задача 4
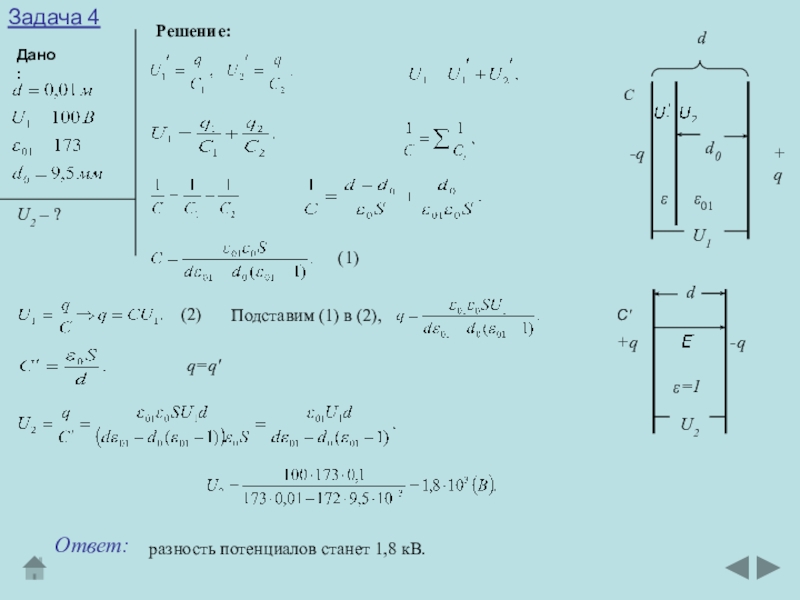
Дано:
U2 – ?
+q
-q
d0
01
U1
d
=1
U2
-q
+q
(1)
(2)
Подставим (1) в (2),
q=q
разность потенциалов станет 1,8 кВ.
Ответ:
Решение:
d
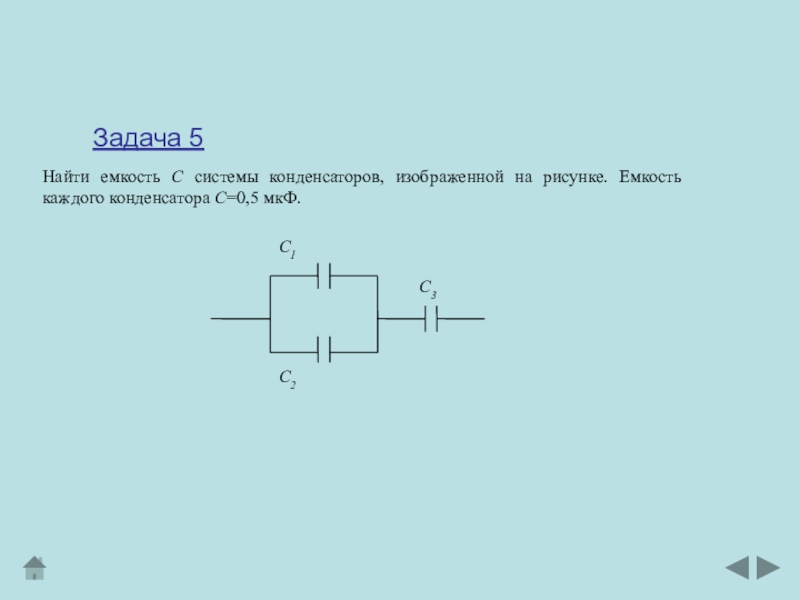
Слайд 12Найти емкость С системы конденсаторов, изображенной на рисунке. Емкость каждого
конденсатора С=0,5 мкФ.
Задача 5
Слайд 13Задача 5
С=0,5 мкФ
С – ?
Дано:
Решение:
C1
C2
C3
емкость системы конденсаторов
составляет
мкФ.
Ответ:
Слайд 14 При помощи электрометра сравнивали между собой емкости
двух конденсаторов. Для этого заряжали их до разностей потенциалов U1=300
В и U2=100 В и соединяли оба конденсатора параллельно. Измеренная при этом разность потенциалов между обкладками конденсатора оказалось равной U=250 В. Найти отношение емкостейЗадача 6
Слайд 15U1 = 300 В
U2 = 100 В
U = 250 В
Дано:
Задача 6
Решение:
C1
U1
+ -
C2
U2
+
-(1)
Подставив значения q1, q2, q1, q2 в выражение (1), получим
поделим на С2
отношение емкостей конденсаторов
Ответ:
Слайд 16Задача 7
Пластины плоского конденсатора площадью
каждая притягиваются друг к
другу с силой F=30 мН. Пространство между пластинами заполнено слюдой. Найти заряды q, находящиеся на пластинах, напряженность Е поля между пластинами и объемную плотность энергии поля.
Слайд 17Дано:
Задача 7
Решение:
(1)
(2)
Подставим (2) в (1) и выразим q
(3)
(4)
Подставим
в (4) выражение (2), получим
(5)
3) Объемная плотность энергии электрического
поля определяется формулой(6)
Подставим (5) в (6)
Ответ:
заряд, находящийся на пластинах, равен
, напряженность поля между пластинами составляет
, объемная плотность энергии электрического поля равна
Слайд 18Плоский конденсатор заполнен диэлектриком, и на его пластины подана некоторая
разность потенциалов. Его энергия при этом W=20 мкДж. После того,
как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую нужно было совершить против сил электрического поля, чтобы вынуть диэлектрик, А=70 мкДж. Найти диэлектрическую проницаемость диэлектрика.Задача 8
Слайд 19Дано:
Задача 8
-q
+q
U
-q
+q
’
U
Подставим (3), (4), (1) в выражение, получаем
диэлектрическая проницаемость
диэлектрика равна
Ответ:
Решение:
(1)
(2)
(3)
(4)
