Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема №9 Матрицы
Содержание
- 1. Тема №9 Матрицы
- 2. Понятие о матрицеТаблица чисел вида, состоящая из
- 3. ОпределенияПри m=0, матрица строка.При n=0, матрица столбец.При
- 4. Равенство матрицДве матрицы А и В называют
- 5. Сложение матрицМатрицы одинакового размера можно сложить. Суммой
- 6. Сложение матрицСложение матриц подчиняется переместительному и сочетательному закону.Матрица все элементы которой равны нулю называется нуль матрицей
- 7. Вычитание матрицРазностью двух матриц А и В одинакового размера называется матрица С, такая чтоАВС
- 8. Умножение матрицы на числоПроизведением матрицы А на
- 9. Умножение матрицЭлемент матрицы произведения, находящийся на пересечении
- 10. Пример умножения матрицПРИМЕР 1ПРИМЕР 2?????РЕШИТЬ21????? РЕШИТЬ
- 11. Пример умножения матрицПРИМЕР 1ПРИМЕР 221
- 12. Пример 3ВЫВОДЫ: В результате перемножения двух матриц
- 13. ПРИМЕР 3??
- 14. ПРИМЕР 3ВЫВОД Произведение двух матриц не подчиняется переместительному законуПроизведение матриц подчиняется сочетательному закону
- 15. Особенность произведения матрицИзвестно, что произведение двух отличных
- 16. Особенность произведения матриц
- 17. Свойство единичной матрицыМатрица вида Е – называется
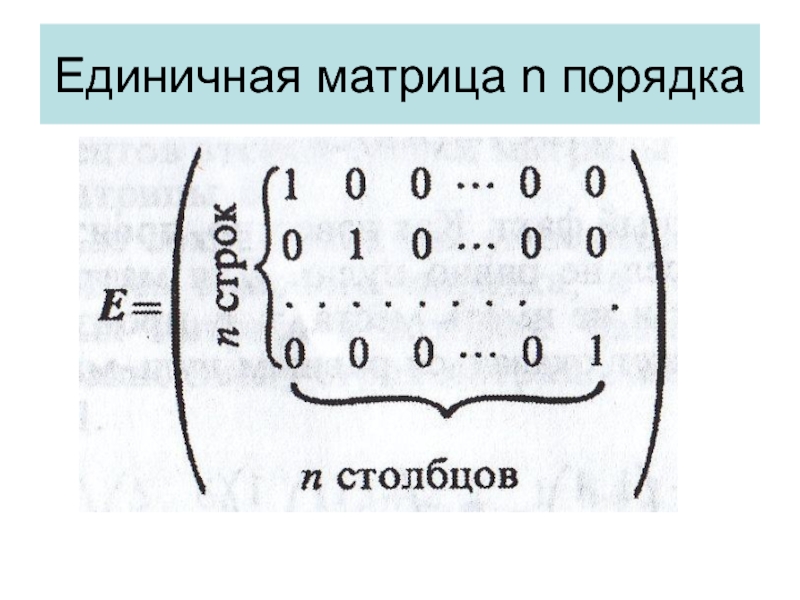
- 18. Единичная матрица n порядка
- 19. Транспонированная матрицаЕсли в матрице А, сделать все
- 20. Диагональная матрицаДиагональная матрица — квадратная матрица, все элементы которой кроме диагональных — нулевые.
- 21. Определитель второго порядкаОпределителем второго порядка, соответствующим матрице А, называется число, равное а11а22-а12а21.ЭЛЕМЕНТЫ ОПРЕДЕЛИТЕЛЯГлавная диагональПобочная диагональ
- 22. Пример вычисления определителя
- 23. Свойства определителяВеличина определителя не меняется, если его
- 24. Определители третьего порядкаОпределителем третьего порядка, соответствующим матрице А, называется число равное а11а22а33+а12а23а31+а13а21а32-а13а22а31-а11а23а32-а12а21а23
- 25. Правило треугольника
- 26. Свойства определителей третьего порядкаВсе свойства определителя второго
- 27. Минор элемента определителяМинором какого-либо элемента определителя называется
- 28. Алгебраическое дополнение элемента определителяНазывается его минор взятый
- 29. ТеоремаОпределитель равен сумме произведений элементов какой либо
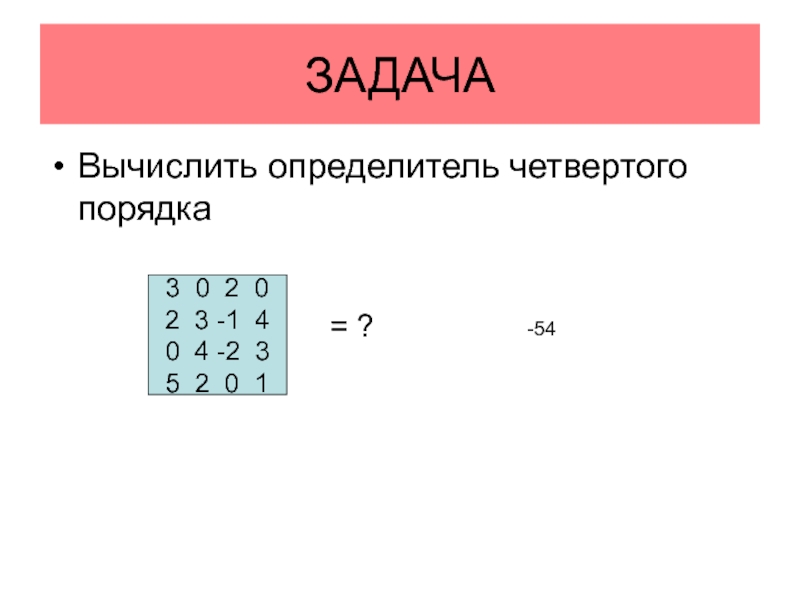
- 30. ЗАДАЧАВычислить определитель четвертого порядка3 0 2 02
- 31. ТеоремаЕсли А и В – квадратные матрицы
- 32. Обратная матрицаТолько для квадратных матриц, имеющих не
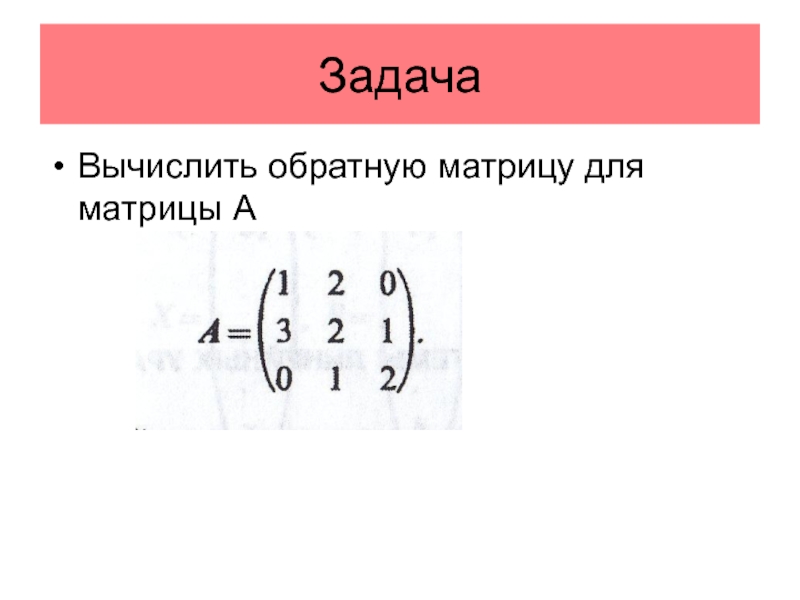
- 33. ЗадачаВычислить обратную матрицу для матрицы А
- 34. РешениеОпределительДополнения
- 35. РЕШЕНИЕ
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Понятие о матрице
Таблица чисел вида, состоящая из m столбцов и
n строк, называется матрицей размера m на n.
Слайд 3Определения
При m=0, матрица строка.
При n=0, матрица столбец.
При m=n, квадратная матрица,
причем число строк и столбцов называют порядком квадратной матрицы.
Матрица второго
порядкаМатрица третьего порядка
Слайд 4Равенство матриц
Две матрицы А и В называют равными А=В, если
они одинакового размера (то есть имеют одинаковое число строк и
столбцов) и их соответствующие элементы равны.Слайд 5Сложение матриц
Матрицы одинакового размера можно сложить. Суммой двух матриц А
и В будет матрица С , элементы которой равны сумме
соответствующих элементов матриц А и В.ПРИМЕР
Слайд 6Сложение матриц
Сложение матриц подчиняется переместительному и сочетательному закону.
Матрица все элементы
которой равны нулю называется нуль матрицей
Слайд 7Вычитание матриц
Разностью двух матриц А и В одинакового размера называется
матрица С, такая что
А
В
С
Слайд 8Умножение матрицы на число
Произведением матрицы А на число L называется
матрица, элементы которой равны произведению числа L на соответствующие элементы
матрицы А.Слайд 9Умножение матриц
Элемент матрицы произведения, находящийся на пересечении i-строки и k-столбца,
представляет собой сумму парных произведений элементов i-строки первой матрицы на
элементы k-столбца второй матрицы.Это правило сохраняется при умножении квадратных матриц и прямоугольных,
у которых число столбцов матрицы множимого равно числу строк матрицы
множителя
Слайд 12Пример 3
ВЫВОДЫ: В результате перемножения двух матриц получается матрица,
содержащая
столько строк сколько их имеет матрица множимое, и столько
столбцов
сколько их имеет матрица множитель.Слайд 14ПРИМЕР 3
ВЫВОД Произведение двух матриц не подчиняется переместительному закону
Произведение матриц
подчиняется сочетательному закону
Слайд 15Особенность произведения матриц
Известно, что произведение двух отличных от нуля чисел
не равно нулю. Для матриц подобное обстоятельство может не выполняться.
ПРОВЕРИТЬ!!!!
Слайд 17Свойство единичной матрицы
Матрица вида Е – называется единичной матрицей. При
умножении любой квадратной матрицы А второго порядка на единичную матрицу
получаем матрицу А.Аналогично ЕА=А
Слайд 19Транспонированная матрица
Если в матрице А, сделать все строки столбцами с
тем же номером, то получим матрицу, которую называют транспонированной к
матрице А.А=
Слайд 20Диагональная матрица
Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных —
нулевые.
Слайд 21Определитель второго порядка
Определителем второго порядка, соответствующим матрице А, называется число,
равное а11а22-а12а21.
ЭЛЕМЕНТЫ ОПРЕДЕЛИТЕЛЯ
Главная диагональ
Побочная диагональ
Слайд 23Свойства определителя
Величина определителя не меняется, если его строки заменить соответствующими
столбцами
Меняется знак, если поменять местами его строки или столбцы.
Увеличивается в
k раз, если элементы какого-либо столбца или строки увеличить в k раз, то есть общий множитель имеющийся в строке или столбце, можно выносить за знак определителя.Равна нулю, если элементы какого-либо его столбца или строки равны нулю.
Равна нулю, если элементы двух строк или столбцов соответственно равны.
Слайд 24Определители третьего порядка
Определителем третьего порядка, соответствующим матрице А, называется число
равное а11а22а33+а12а23а31+а13а21а32-а13а22а31-а11а23а32-а12а21а23
Слайд 26Свойства определителей третьего порядка
Все свойства определителя второго порядка остаются справедливыми
для определителей третьего порядка
Единичная матрица третьего порядка
Слайд 27Минор элемента определителя
Минором какого-либо элемента определителя называется определитель, полученный из
данного вычеркиванием той строки и столбца, которым принадлежит данный элемент.
Например
минором а12 является= M12
Слайд 28Алгебраическое дополнение элемента определителя
Называется его минор взятый со знаком минус
Порядок
в строке
Порядок в столбце
Если сумма I и k четно ,
то А имеет знак минус.Если сумма I и k нечетно, то А имеет знак плюс.
Слайд 29Теорема
Определитель равен сумме произведений элементов какой либо строки или столбца
на их алгебраические дополнения.
ДОКАЗАТЕЛЬСТВО:
Данная формула называется разложением определителя по элементам
первой строкидополнение
Слайд 31Теорема
Если А и В – квадратные матрицы одного порядка с
определителями !А! и !В!, то определитель матрицы С = АВ
равен произведению определителей умножаемых матриц.Слайд 32Обратная матрица
Только для квадратных матриц, имеющих не нулевой определитель.
Если А
– квадратная матрица, то обратной для нее матрицей называется матрица,
удовлетворяющая условиюДополнения элемента а11
Чтобы построить обратную матрицу, необходимо
Сначала каждый элемент заменить его алгебраическим
дополнением, деленным на определитель, а затем.
построить транспонированную матрицу.