Тема: Задачи на построение сечений. Амеличев, Музычкин, Молчанова, Полун

Содержание

1. Тема: Задачи на построение сечений. Амеличев, Музычкин, Молчанова, Полун
2. Секущей плоскостью многогранника называется такая плоскость, по
3. Секущая плоскость пересекает грани многогранника по отрезкам,
4. Две плоскости пересекаются по прямой (эта
5. ABCDB1C1D1MNKВыбираем точки М и N, принадлежащие одной
6. ABCDB1C1D1MNKA1EТеперь обращаем внимание, что ребро куба В1С1
7. ABCDB1C1D1MNKA1EТочки Е и К принадлежат верхней грани
8. ABCDB1C1D1MNKA1EFДалее видим, что ребро куба А1В1 лежит
9. ABCDB1C1D1MNKA1EFGПолученная точка G лежит в одной грани
10. ABCDC1D1MNKA1EFGHОстается соединить отрезками все пары точек, лежащие
11. Плоскость сечения может задаваться: 1) тремя точками,
12. Данный метод построения сечений многогранников можно применять,
13. Скачать презентанцию

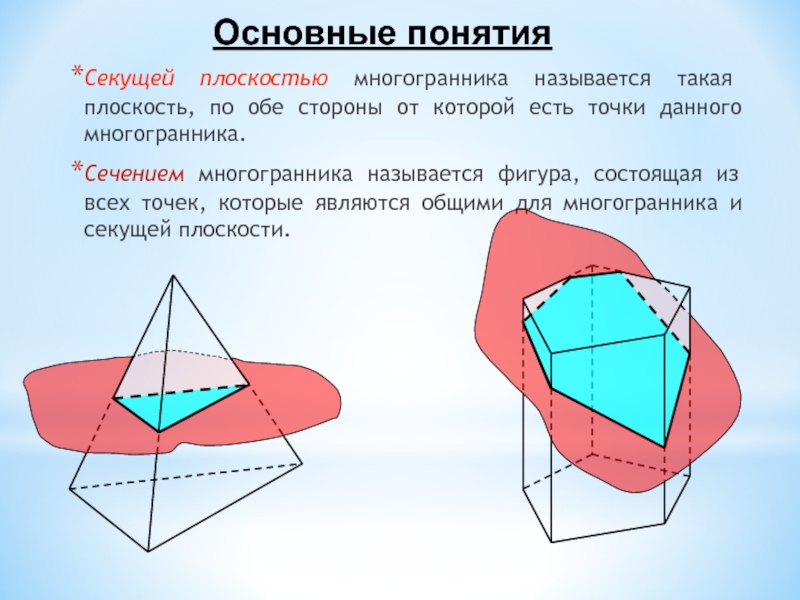
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника.Сечением многогранника называется фигура, состоящая из всех точек, которые являются общими для многогранника и секущей плоскости.Основные понятия

Главная
Разное
Тема: Задачи на построение сечений. Амеличев, Музычкин, Молчанова, Полун

Слайды и текст этой презентации

Слайд 1Тема: « Задачи на построение сечений».
Амеличев, Музычкин,

Молчанова, Полун. 10«В».

Слайд 2Секущей плоскостью многогранника называется такая плоскость, по обе стороны от

которой есть точки данного многогранника.
Сечением многогранника называется фигура, состоящая из

всех точек, которые являются общими для многогранника и секущей плоскости.

Основные понятия

Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника.Сечением многогранника называется

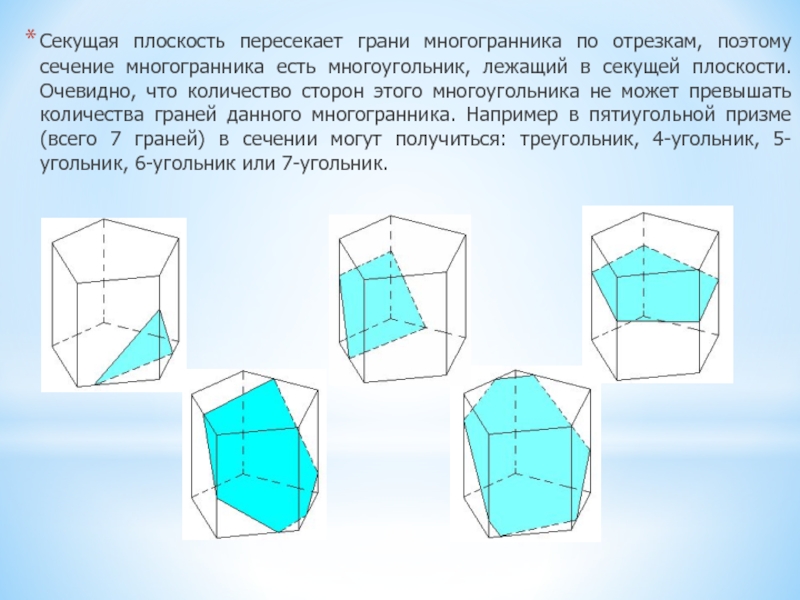
Слайд 3Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника

есть многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон

этого многоугольника не может превышать количества граней данного многогранника. Например в пятиугольной призме (всего 7 граней) в сечении могут получиться: треугольник, 4-угольник, 5-угольник, 6-угольник или 7-угольник.

Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть многоугольник, лежащий в секущей плоскости. Очевидно,

Слайд 4 Две плоскости пересекаются по прямой (эта аксиома и дала

названию метода – под «следом» понимается прямая пересечения какой-либо грани

многогранника и секущей плоскости).
Получение «следа» сводится к получению двух точек, принадлежащих одновременно какой-нибудь грани многогранника и секущей плоскости (подумайте, почему именно двух!?).
Точки получаются как пересечение двух прямых, принадлежащих одной и той же плоскости.

Проследим на примере построение сечения куба плоскостью, заданной тремя данными точками M, N и K.

Метод «следов»

Две плоскости пересекаются по прямой (эта аксиома и дала названию метода – под «следом» понимается прямая

Слайд 5A
B
C
D
B1
C1
D1
M
N
K
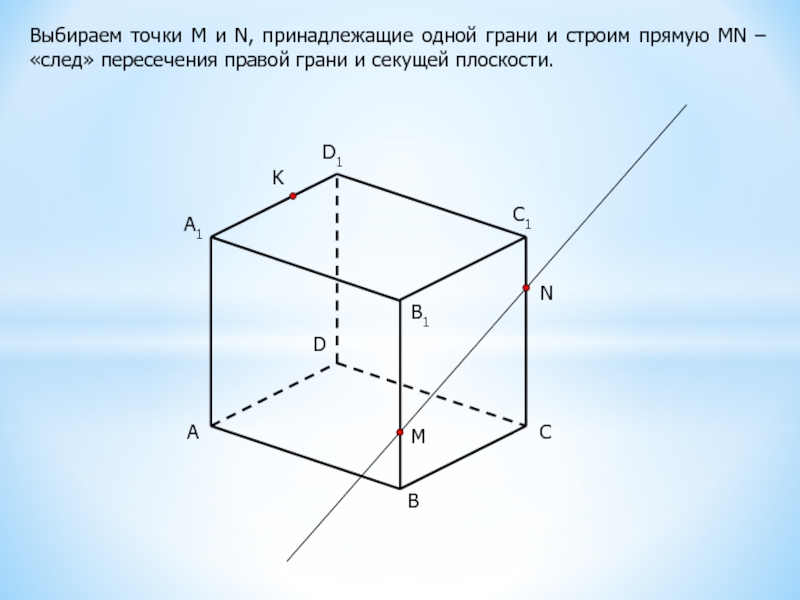
Выбираем точки М и N, принадлежащие одной грани и строим

прямую MN – «след» пересечения правой грани и секущей плоскости.
A1

ABCDB1C1D1MNKВыбираем точки М и N, принадлежащие одной грани и строим прямую MN – «след» пересечения правой грани

Слайд 6A
B
C
D
B1
C1
D1
M
N
K
A1
E
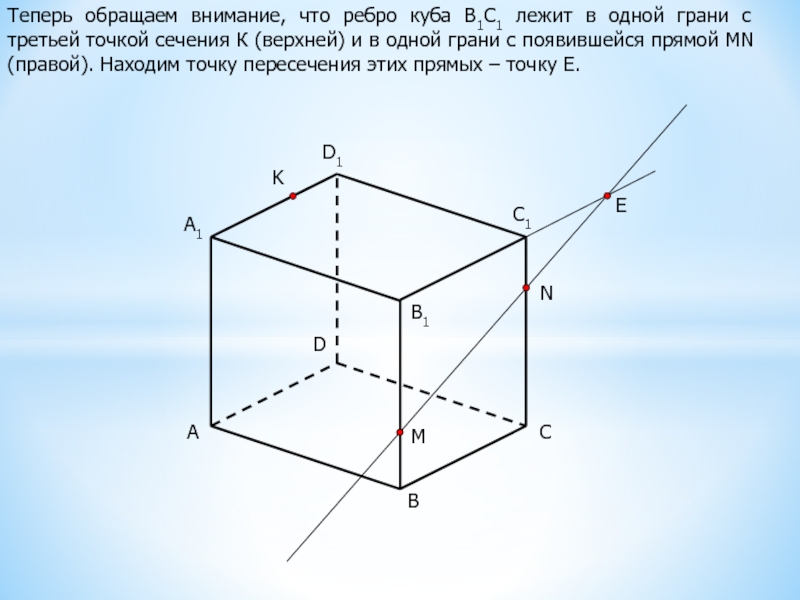
Теперь обращаем внимание, что ребро куба В1С1 лежит в одной

грани с третьей точкой сечения К (верхней) и в одной

грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е.

ABCDB1C1D1MNKA1EТеперь обращаем внимание, что ребро куба В1С1 лежит в одной грани с третьей точкой сечения К (верхней)

Слайд 7A
B
C
D
B1
C1
D1
M
N
K
A1
E
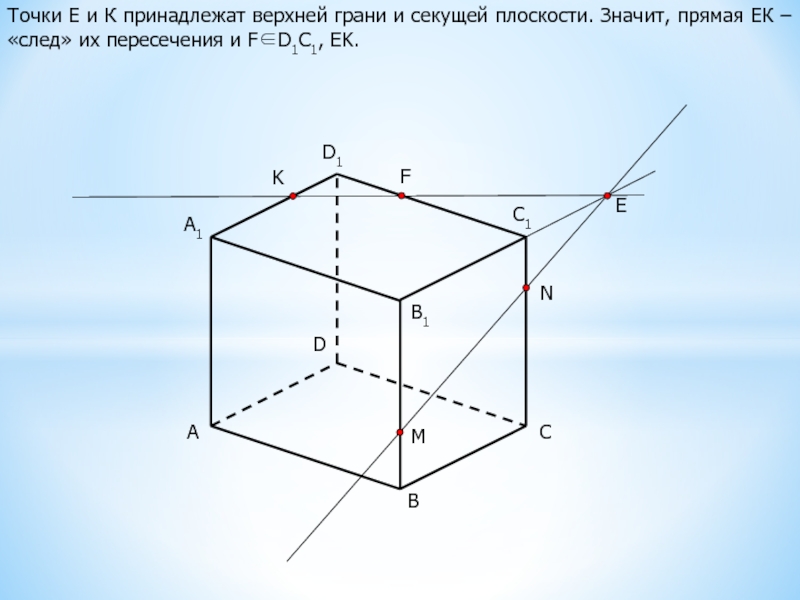
Точки Е и К принадлежат верхней грани и секущей плоскости.

Значит, прямая ЕК – «след» их пересечения и FD1C1, EK.
F

ABCDB1C1D1MNKA1EТочки Е и К принадлежат верхней грани и секущей плоскости. Значит, прямая ЕК – «след» их пересечения

Слайд 8A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
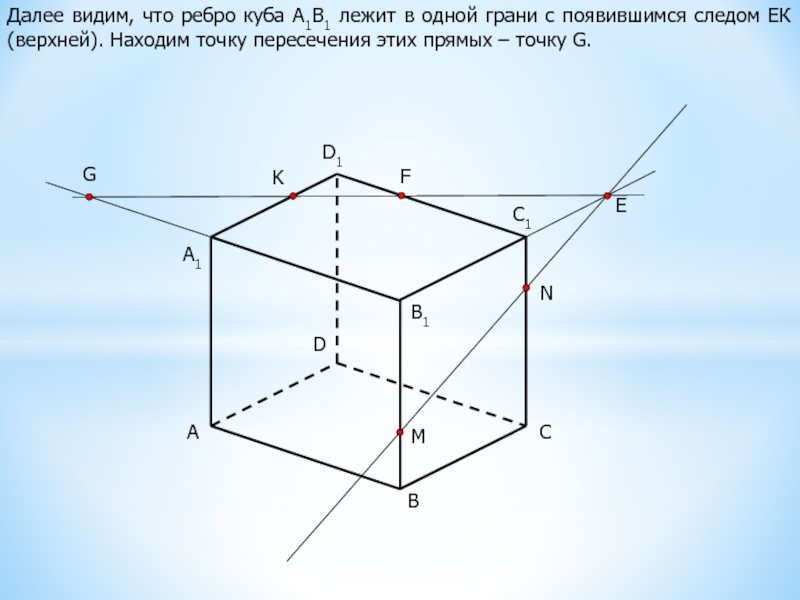
Далее видим, что ребро куба А1В1 лежит в одной грани

с появившимся следом ЕК (верхней). Находим точку пересечения этих прямых

– точку G.

ABCDB1C1D1MNKA1EFДалее видим, что ребро куба А1В1 лежит в одной грани с появившимся следом ЕК (верхней). Находим точку

Слайд 9A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
G
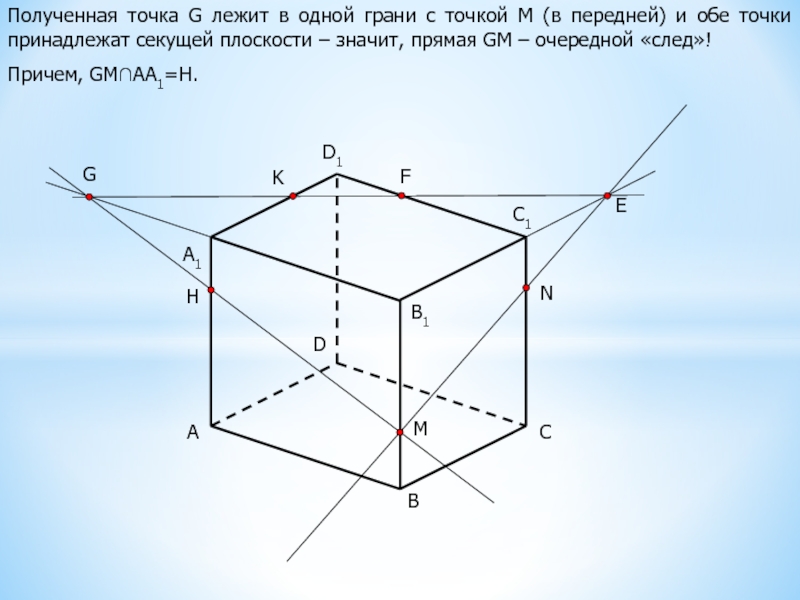
Полученная точка G лежит в одной грани с точкой М

(в передней) и обе точки принадлежат секущей плоскости – значит,

прямая GM – очередной «след»!
Причем, GM∩АА1=Н.

ABCDB1C1D1MNKA1EFGПолученная точка G лежит в одной грани с точкой М (в передней) и обе точки принадлежат секущей

Слайд 10A
B
C
D
C1
D1
M
N
K
A1
E
F
G
H
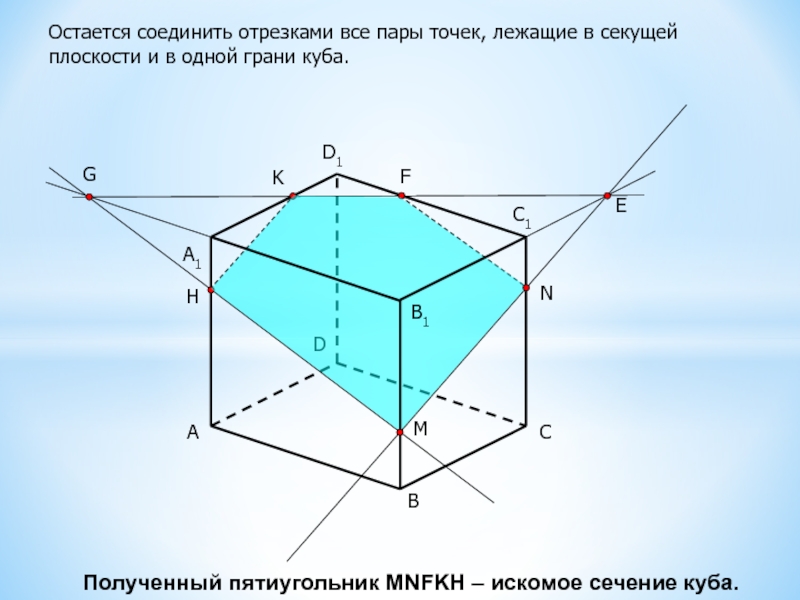
Остается соединить отрезками все пары точек, лежащие в секущей плоскости

и в одной грани куба.
Полученный пятиугольник MNFKH – искомое

сечение куба.

ABCDC1D1MNKA1EFGHОстается соединить отрезками все пары точек, лежащие в секущей плоскости и в одной грани куба. Полученный пятиугольник

Слайд 11Плоскость сечения может задаваться:
1) тремя точками, не лежащими на

одной прямой;
2) прямой и точкой, не лежащей на ней;
3)

двумя пересекающимися прямыми;
4) двумя параллельными прямыми.
Все эти случаи можно свести к первому, выбирая на прямых удобные для нас точки.

Плоскость сечения может задаваться: 1) тремя точками, не лежащими на одной прямой; 2) прямой и точкой, не

Слайд 12Данный метод построения сечений многогранников можно применять, если найдется хотя

бы одна пара точек, лежащих в секущей плоскости и одной

грани многогранника. После чего задача циклично алгоритмизируется в получение очередной точки и очередного «следа».
ПРИМЕЧАНИЕ. Если такой пары точек не найдется, то сечение строится методом параллельных проекций.

Данный метод построения сечений многогранников можно применять, если найдется хотя бы одна пара точек, лежащих в секущей

Скачать презентацию

Разделы презентаций

Тема: Задачи на построение сечений. Амеличев, Музычкин, Молчанова, Полун

Содержание

Слайды и текст этой презентации

Слайд 1Тема: « Задачи на построение сечений».
Амеличев, Музычкин,

Молчанова, Полун. 10«В».

Слайд 2Секущей плоскостью многогранника называется такая плоскость, по обе стороны от

которой есть точки данного многогранника.
Сечением многогранника называется фигура, состоящая из

Слайд 3Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника

есть многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон

Слайд 4 Две плоскости пересекаются по прямой (эта аксиома и дала

названию метода – под «следом» понимается прямая пересечения какой-либо грани

Слайд 5A
B
C
D
B1
C1
D1
M
N
K
Выбираем точки М и N, принадлежащие одной грани и строим

прямую MN – «след» пересечения правой грани и секущей плоскости.
A1

Слайд 6A
B
C
D
B1
C1
D1
M
N
K
A1
E
Теперь обращаем внимание, что ребро куба В1С1 лежит в одной

грани с третьей точкой сечения К (верхней) и в одной

Слайд 7A
B
C
D
B1
C1
D1
M
N
K
A1
E
Точки Е и К принадлежат верхней грани и секущей плоскости.

Значит, прямая ЕК – «след» их пересечения и FD1C1, EK.
F

Слайд 8A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
Далее видим, что ребро куба А1В1 лежит в одной грани

с появившимся следом ЕК (верхней). Находим точку пересечения этих прямых

Слайд 9A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
G
Полученная точка G лежит в одной грани с точкой М

(в передней) и обе точки принадлежат секущей плоскости – значит,

Слайд 10A
B
C
D
C1
D1
M
N
K
A1
E
F
G
H
Остается соединить отрезками все пары точек, лежащие в секущей плоскости

и в одной грани куба.
Полученный пятиугольник MNFKH – искомое

Слайд 11Плоскость сечения может задаваться:
1) тремя точками, не лежащими на

одной прямой;
2) прямой и точкой, не лежащей на ней;
3)

Слайд 12Данный метод построения сечений многогранников можно применять, если найдется хотя

бы одна пара точек, лежащих в секущей плоскости и одной

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Тема: Задачи на построение сечений. Амеличев, Музычкин, Молчанова, Полун

Содержание

Слайды и текст этой презентации

Слайд 1Тема: « Задачи на построение сечений». Амеличев, Музычкин,

Молчанова, Полун. 10«В».

Слайд 2Секущей плоскостью многогранника называется такая плоскость, по обе стороны от

которой есть точки данного многогранника.Сечением многогранника называется фигура, состоящая из

Слайд 3Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника

есть многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон

Слайд 4 Две плоскости пересекаются по прямой (эта аксиома и дала

названию метода – под «следом» понимается прямая пересечения какой-либо грани

Слайд 5ABCDB1C1D1MNKВыбираем точки М и N, принадлежащие одной грани и строим

прямую MN – «след» пересечения правой грани и секущей плоскости.A1

Слайд 6ABCDB1C1D1MNKA1EТеперь обращаем внимание, что ребро куба В1С1 лежит в одной

грани с третьей точкой сечения К (верхней) и в одной

Слайд 7ABCDB1C1D1MNKA1EТочки Е и К принадлежат верхней грани и секущей плоскости.

Значит, прямая ЕК – «след» их пересечения и FD1C1, EK.F

Слайд 8ABCDB1C1D1MNKA1EFДалее видим, что ребро куба А1В1 лежит в одной грани

с появившимся следом ЕК (верхней). Находим точку пересечения этих прямых

Слайд 9ABCDB1C1D1MNKA1EFGПолученная точка G лежит в одной грани с точкой М

(в передней) и обе точки принадлежат секущей плоскости – значит,

Слайд 10ABCDC1D1MNKA1EFGHОстается соединить отрезками все пары точек, лежащие в секущей плоскости

и в одной грани куба. Полученный пятиугольник MNFKH – искомое

Слайд 11Плоскость сечения может задаваться: 1) тремя точками, не лежащими на

одной прямой; 2) прямой и точкой, не лежащей на ней;3)

Слайд 12Данный метод построения сечений многогранников можно применять, если найдется хотя

бы одна пара точек, лежащих в секущей плоскости и одной

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Тема: « Задачи на построение сечений».
Амеличев, Музычкин,

которой есть точки данного многогранника.
Сечением многогранника называется фигура, состоящая из

Слайд 5A
B
C
D
B1
C1
D1
M
N
K
Выбираем точки М и N, принадлежащие одной грани и строим

прямую MN – «след» пересечения правой грани и секущей плоскости.
A1

Слайд 6A
B
C
D
B1
C1
D1
M
N
K
A1
E
Теперь обращаем внимание, что ребро куба В1С1 лежит в одной

Слайд 7A
B
C
D
B1
C1
D1
M
N
K
A1
E
Точки Е и К принадлежат верхней грани и секущей плоскости.

Значит, прямая ЕК – «след» их пересечения и FD1C1, EK.
F

Слайд 8A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
Далее видим, что ребро куба А1В1 лежит в одной грани

Слайд 9A
B
C
D
B1
C1
D1
M
N
K
A1
E
F
G
Полученная точка G лежит в одной грани с точкой М

Слайд 10A
B
C
D
C1
D1
M
N
K
A1
E
F
G
H
Остается соединить отрезками все пары точек, лежащие в секущей плоскости

и в одной грани куба.
Полученный пятиугольник MNFKH – искомое

Слайд 11Плоскость сечения может задаваться:
1) тремя точками, не лежащими на

одной прямой;
2) прямой и точкой, не лежащей на ней;
3)