Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Температурное поле
Содержание
- 1. Температурное поле
- 2. Температурное полесовокупность значений температуры во всех точках
- 3. Температурное поле стационарное температура во всех
- 4. Слайд 4
- 5. Изотермическая поверхностьсемейство изотерм, отличающихся на ∆t
- 6. Изотермическая поверхностьгеометрическое место точек, температура которых одинаковаизотермические
- 7. Пересечение изотермических поверхностей плоскостью дает семейство изотерм,
- 8. Градиент температурыГрадиент температуры в теплообменнике градирни с
- 9. Градиент температурывектор, направленный по нормали к изометрической
- 10. Тепловой потокколичество теплоты, проходящее через изотермическую поверхность F в единицу времени называется Q[Вт=Дж/с]
- 11. Плотность теплового потокаудельный тепловой поток qколичество теплоты,
- 12. Слайд 12
- 13. Закон Фурье (основное уравнение теплопроводности) В
- 14. Коэффициент теплопроводностиλмножитель пропорциональностихарактеризует способность вещества проводить теплоту через себя
- 15. Коэффициент теплопроводностипоказывает, какое количество теплоты проходит вследствие
- 16. Закон Фурьеплотность теплового потока пропорциональна градиенту температурыт.е.
- 17. Слайд 17
- 18. В целом коэффициент теплопроводности убывает с уменьшением
- 19. Дифференциальное уравнение теплопроводностиустанавливает связь между величинами, характеризующими
- 20. При выводе уравнения рассмотрим сначала сплошную, однородную,
- 21. Получим следующее уравнение
- 22. Коэффициент температуропроводностихарактеризует скорость изменения температуры в нестационарных
- 23. Дифференциальное уравнение теплопроводности выведено на основе общих
- 24. Краевые условия1 геометрические условия, характеризующие форму и
- 25. Слайд 25
- 26. Граничное условие первого родазадается распределение температуры на
- 27. Граничное условие второго родаЗадается величина теплового потока
- 28. Согласно закону Фурье плотность теплового потока пропорциональна
- 29. Граничное условие третьего родаГраничное условие третьего рода
- 30. При граничных условиях третьего рода на границе
- 31. Граничное условие четвертого родаявляется условием контактного теплообмена
- 32. Процесс теплопередачиВ большинстве технологических процессов теплообмен между
- 33. Теплопередача через однородную стенку
- 34. Пусть плоская однородная стенка имеет толщину δ.Дано:коэффициент
- 35. Используя закон Ньютона-Рихмана распишем тепловой поток от
- 36. Коэффициент теплопередачиВыразим плотность теплового потока получимгде k
- 37. Характеризует интенсивность передачи тепла от одной жидкости к другой через разделяющую их стенку
- 38. Численное значение коэффициента k определяется количеством теплоты,
- 39. Термическое сопротивление теплопередачиВеличина, обратная коэффициенту теплопередачи, называется
- 40. Полное термическое сопротивление складывается из частных термических
- 41. Термическое сопротивление теплопередачи через многослойную стенкуКоэффициент теплопередачи для многослойной стенки
- 42. Удельный тепловой поток через многослойную стенку
- 43. Тепловой поток через поверхность стенкиТемпературы поверхностей однородной стенки
- 44. Температура стенки на границе соприкосновения двух слоев
- 45. Интенсификация теплопередачи При заданных размерах стенки и температурах
- 46. Виды ребристых поверхностей
- 47. Основные требования к ребристым поверхностям1. Ребра
- 48. Движущая сила тепловых процессовразность температур взаимодействующих средВ
- 49. Основное уравнение теплопередачиколичество теплоты, передаваемое в единицу
- 50. Схемы движения теплоносителейБольшое влияние на процесс теплообмена
- 51. Слайд 51
- 52. (а) параллельное однонаправленное течение, или прямоток -
- 53. (в)перекрестный ток , при котором теплоносители движутся
- 54. Выбор взаимного направления движения теплоносителей
- 55. Для случая прямотока конечная температура менее нагретого
- 56. Таким образом, противоток является более предпочтительным при
- 57. Конфигурации теплообменников в зависимости от схемы движения
- 58. Противоток. В противоточном теплообменнике два теплоносителя движутся
- 59. Прямоток. В теплообменниках этого типа два теплоносителя
- 60. Перекрестный ток. В теплообменнике с перекрестным током
- 61. Передача теплоты конвекциейКонвекция (конвективная теплоотдача)перенос тепла вследствие
- 62. вынужденная – жидкость или газ движутся за
- 63. Закон теплоотдачи (Ньютона-Рихмана)Для удобства расчета теплоотдачи берут
- 64. Коэффициент теплоотдачихарактеризует количество теплоты, которое передается от
- 65. от переменных, определяющих режим течения жидкости -
- 66. Зависимость коэффициента теплоотдачи от этих факторов очень
- 67. Дифференциальное уравнение конвективного теплообменаИсходной зависимостью для обобщения
- 68. Выделим в установившимся потоке жидкости элементарный параллелепипед
- 69. Слайд 69
- 70. Уравнение Фурье-Кирхгофа (дифференциальное уравнение конвективного теплообмена)это уравнение
- 71. Из уравнения Фурье-Кирхгофа следует, что температурное поле
- 72. Подобные процессыявления, принадлежащие одному и тому же
- 73. Общие условия подобия физических процессов (по Кирпичеву
- 74. С помощью теории подобия размерные физические величины
- 75. Теория подобия устанавливает условия, при которых результаты
- 76. К ним относятся:число Рейнольдса характеризует соотношение между
- 77. 2) число Нуссельтахарактеризует интенсивность теплообмена на границе
- 78. 3) число Пеклехарактеризует соотношение между теплотой, переносимой путем конвекции, и теплопроводностьюPe=vl/aa - коэффициент температуропроводности, кв.м/с
- 79. 4) число Прандтляхарактеризует подобие физических свойств теплоносителей в процессах конвективного теплообменаPr=cμ/λc – удельная теплоемкость жидкости, Дж/кг·К
- 80. Слайд 80
- 81. Скачать презентанцию
Температурное полесовокупность значений температуры во всех точках изучаемого пространства в данный момент времениt=f(x, y, z, τ)x, y, z – координаты точки, τ - время
Слайды и текст этой презентации
Слайд 1Температурное поле
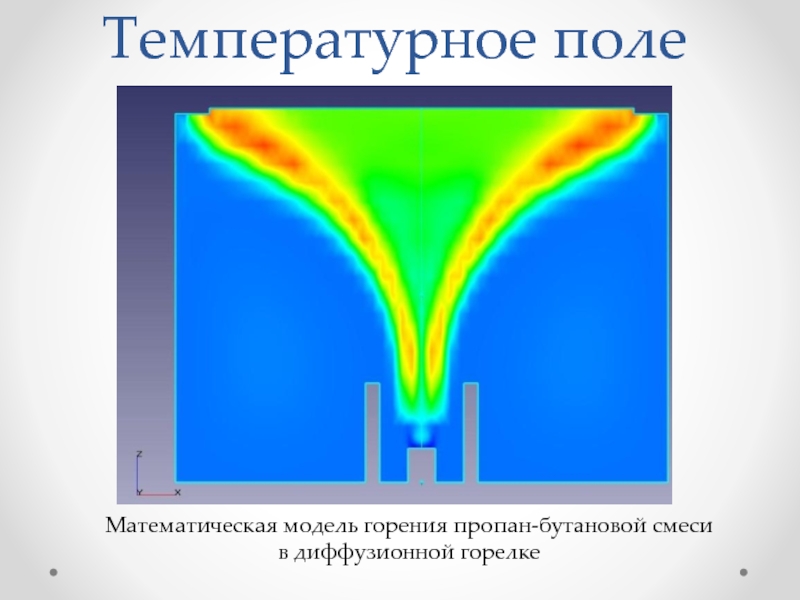
Математическая модель горения пропан-бутановой смеси
в диффузионной горелке
Слайд 2Температурное поле
совокупность значений температуры во всех точках изучаемого пространства в
данный момент времени
точки, τ - время
Слайд 3Температурное поле
стационарное
температура во всех точках пространства не зависит
от времени
t=f(x, y, z, τ)
∂t/∂τ=0нестационарное
температура зависит от времени, что соответствует неустановившемуся тепловому режиму
t=f(x, y, z, τ) ∂t/∂τ≠0
Слайд 6Изотермическая поверхность
геометрическое место точек, температура которых одинакова
изотермические поверхности не пересекаются
– они либо оканчиваются на поверхности тела, либо целиком лежат
внутри тела
Слайд 7Пересечение изотермических поверхностей плоскостью дает семейство изотерм, которые обладают свойствами
изотермических поверхностей
Температура в теле может изменяться только в направлениях, пересекающих
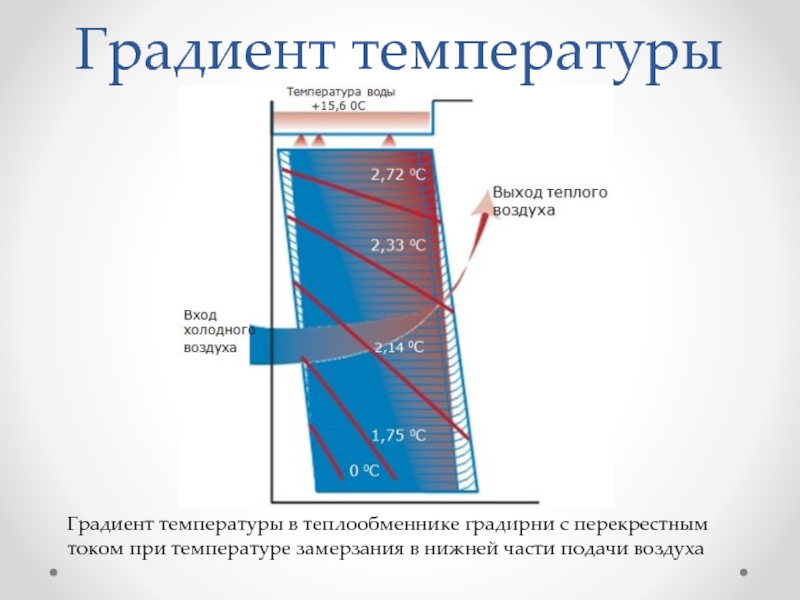
изотермические поверхности
Слайд 8Градиент температуры
Градиент температуры в теплообменнике градирни с перекрестным током при
температуре замерзания в нижней части подачи воздуха
Слайд 9Градиент температуры
вектор, направленный по нормали к изометрической поверхности в сторону
возрастания температуры и численно равный производной от температуры по этому
направлениюgrad t=∂t/∂n
Слайд 10Тепловой поток
количество теплоты, проходящее через изотермическую поверхность F в единицу
времени называется
Q
[Вт=Дж/с]
![Тепловой потокколичество теплоты, проходящее через изотермическую поверхность F в единицу времени называется Q[Вт=Дж/с]](/img/thumbs/a96e35157183f13a17b8233eff861351-800x.jpg "Температурное поле Тепловой потокколичество теплоты, проходящее через изотермическую поверхность F в единицу времени называется Q[Вт=Дж/с]")
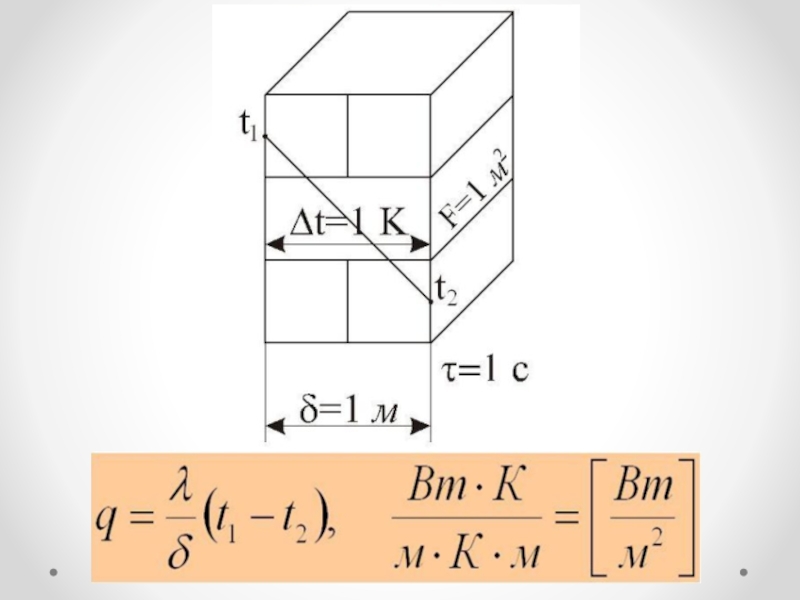
Слайд 11Плотность теплового потока
удельный тепловой поток
q
количество теплоты, проходящее через стенку
1 кв.м за время 1 с
или
тепловой поток отнесенный к
единице поверхности
Слайд 13Закон Фурье
(основное уравнение теплопроводности)
В 1822 году французский математик
и физик Фурье экспериментально установил
количество переданного тепла пропорционально времени, площади
сечения, перпендикулярного направлению распространению тепла, и градиенту температурыМинус в правой части показывает, что в направлении теплового потока температура убывает и величина
grad t является величиной отрицательной
Слайд 14Коэффициент теплопроводности
λ
множитель пропорциональности
характеризует способность вещества проводить теплоту через себя
Слайд 15Коэффициент теплопроводности
показывает, какое количество теплоты проходит вследствие теплопроводности в единицу
времени через стенку толщиной 1 м и площадью 1 кв.
м при разности температур ее поверхностей 1 К. Размерность этого коэффициента – Вт/м·КЗначение коэффициента теплопроводности зависит от природы вещества и его температуры.
Слайд 16Закон Фурье
плотность теплового потока пропорциональна градиенту температуры
т.е. коэффициент теплопроводности -
это тепловой поток, передаваемый через единичную поверхность при единичном значении
температурного градиента
Слайд 18В целом коэффициент теплопроводности убывает с уменьшением плотности
В неметаллических твердых
телах λ растет с увеличением температуры, а также с ростом
плотности веществаДля порошкообразных и пористых тел λ сильно зависит от их объемной плотности – растет с ее увеличением, так как теплопроводность заполняющего поры воздуха существенно меньше теплопроводности твердых компонентов пористого материала
Слайд 19Дифференциальное уравнение теплопроводности
устанавливает связь между величинами, характеризующими процесс передачи теплоты
теплопроводностью
Впервые вывод дифференциального уравнения был предложен М.В. Остроградским в
1830 г. При установлении зависимостей между величинами удобно воспользоваться методами математической физики, которая рассматривает протекание процесса не во всем изучаемом пространстве, а в элементарном объеме вещества в течение бесконечно малого отрезка времени
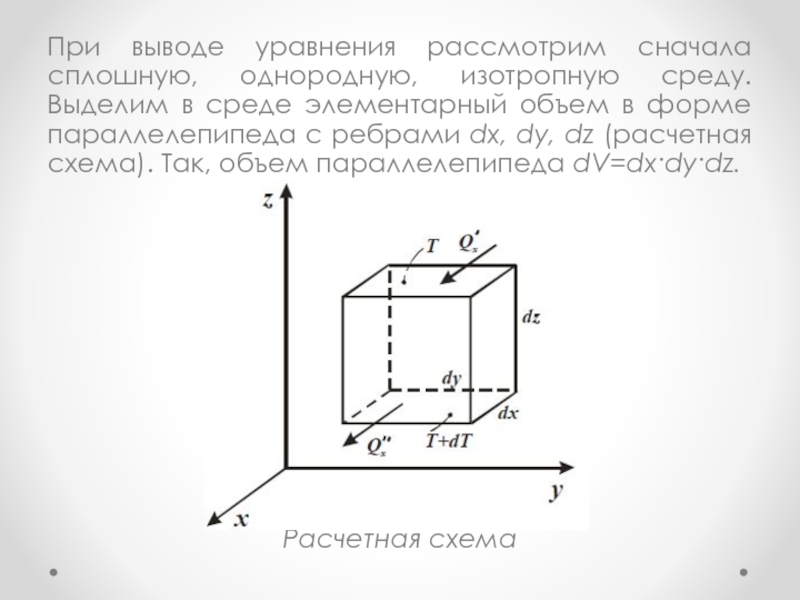
Слайд 20При выводе уравнения рассмотрим сначала сплошную, однородную, изотропную среду. Выделим
в среде элементарный объем в форме параллелепипеда с ребрами dx,
dy, dz (расчетная схема). Так, объем параллелепипеда dV=dx·dy·dz.Расчетная схема
Слайд 22Коэффициент температуропроводности
характеризует скорость изменения температуры в нестационарных процессах
является мерой теплоинерционных
свойств тела
Скорость изменения температуры будет тем выше, чем больше коэффициент
температуропроводностизависит от природы вещества – для металлов больше, чем для жидкостей и газов
[м2/с]
Слайд 23Дифференциальное уравнение теплопроводности выведено на основе общих законов физики и
описывает процесс теплопроводности в самом общем виде.
Для описания конкретного процесса
теплопроводности необходимо рассмотреть все его частные особенности, которые называются условиями однозначности или краевыми условиями.
Слайд 24Краевые условия
1 геометрические условия, характеризующие форму и размеры тела, в
котором протекает процесс
2 физические условия, характеризующие физические свойства тела (теплопроводность,
теплоемкость, плотность, мощность внутренних источников тепла и т.д.)3 временные или начальные условия, характеризующие распределение температуры в изучаемом теле в начальный момент времени – при τ=0 t=f(x, y, z, τ)
4 граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой
Слайд 26Граничное условие первого рода
задается распределение температуры на поверхности тела для
каждого момента времени Тп=f(x, y, z, τ);
частный случай Тп
=constНа поверхности в каждый момент времени решение должно удовлетворять заданному условию, при этом внутри тела температура может возрастать, уменьшаться или быть постоянной
Слайд 27Граничное условие второго рода
Задается величина теплового потока для каждой точки
поверхности тела и для любого момента времени qп=f(x, y, z,
τ); частный случай qп =constнапример, нагревание металлических изделий в высокотемпературных печах
Слайд 28Согласно закону Фурье плотность теплового потока пропорциональна градиенту температуры, поэтому
при граничных условиях второго рода возможно задание градиента температуры на
поверхности в каждый момент времениГрадиент температуры численно равен tg α - тангенсу угла наклона касательной к графику
изменения температуры на поверхности (см. рисунок), поэтому при таких граничных условиях
решение должно удовлетворять заданному углу наклона α в каждый момент времени, а
температура поверхности может быть различной
Слайд 29Граничное условие третьего рода
Граничное условие третьего рода является условием конвективной
теплоотдачи, когда поверхность тела омывается подвижным теплоносителем
задается связь между градиентом
температуры и температурой на поверхности, которая определяется законом теплоотдачи между поверхностью тела и окружающей средой, так называемым законом Ньютона–Рихманаq –плотность теплового потока, Вт/м2
α – коэффициент теплоотдачи, Вт/( м2 К)
Tп – температура поверхности, К
Tср – температура окружающей среды, К
Слайд 30При граничных условиях третьего рода на границе должно выполняться равенство
Т.е.
чем выше температура поверхности, тем больше градиент температуры в теле
на поверхности и, следовательно, тепловой поток с поверхности
Слайд 31Граничное условие четвертого рода
является условием контактного теплообмена и задается равенством
плотностей теплового потока на границе контактирующих сред (индексы 1 и
2 относятся к соответствующей среде)Таким образом, решение дифференциального уравнения теплопроводности при заданных условиях однозначности позволяет определить температурное поле во всем объеме тела для любого момента времени
Слайд 32Процесс теплопередачи
В большинстве технологических процессов теплообмен между теплоносителями происходит через
некоторую поверхность раздела.
Передача тепла от одной жидкой среды (жидкости
или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей.Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенку к более холодной подвижной среде.
Слайд 34Пусть плоская однородная стенка имеет толщину δ.
Дано:
коэффициент теплопроводности λ
температуры окружающей
среды tж1 и tж2
коэффициенты теплоотдачи α1 и α2
Будем считать, что
tж1, tж2, α1 и α2 постоянны и не меняются вдоль поверхности, что позволит рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки.При заданных условиях нужно найти тепловой поток от горячей жидкости к холодной, а также температуры на поверхностях стенки.
Слайд 35Используя закон Ньютона-Рихмана распишем
тепловой поток от горячей жидкости к
стенке
q= α1(tж1 – tc1)
тепловой поток путем теплопроводности через твердую
стенку q= λ(tж1 – tc1) /δтепловой поток от второй поверхности стенки к холодной жидкости за счет теплоотдачи
q= α2(tс2 – tж2)
Выразив температурные напоры (разность характерных температур среды и стенки) получим
Слайд 36Коэффициент теплопередачи
Выразим плотность теплового потока получим
где k – коэффициент теплопередачи
(без учета загрязнений с обеих сторон стенки)
Слайд 37Характеризует интенсивность передачи тепла от одной жидкости к другой через
разделяющую их стенку
Слайд 38
Численное значение коэффициента k определяется количеством теплоты, которое передается от
одного теплоносителя к другому через разделяющую их стенку площадью 1
кв.м в течение 1 с при разности температур теплоносителей 1 К.Размерность коэффициента теплопередачи – Вт/кв.м·К
Слайд 39Термическое сопротивление теплопередачи
Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи
R, а величина δ/λ - термическим сопротивлением стенки.
R =
1/α1+ δ/λ +1/α2
Слайд 40Полное термическое сопротивление складывается из частных термических сопротивлений:
R1=1/α1 – термическое
сопротивление теплоотдачи от горячей жидкости к поверхности стенки
Rc= δ/λ –
термическое сопротивление теплопроводности стенкиR2= 1/α2 – термическое сопротивление теплоотдачи от поверхности стенки к холодной жидкости
Слайд 41Термическое сопротивление теплопередачи
через многослойную стенку
Коэффициент теплопередачи для многослойной стенки
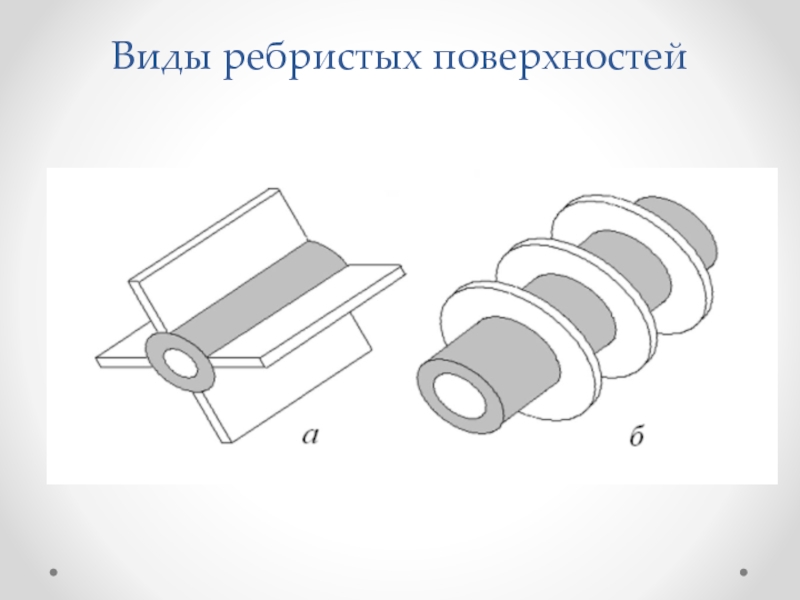
Слайд 45Интенсификация теплопередачи
При заданных размерах стенки и температурах жидкостей величиной, определяющей
теплопередачу, является коэффициент теплопередачи k.
Если значение коэффициента теплоотдачи α мало,
то термическое сопротивление можно уменьшить путем увеличения соответствующей поверхности.Способ интенсификации теплопередачи - оребрение поверхностей
Слайд 47Основные требования
к ребристым поверхностям
1. Ребра целесообразно выполнять из материала
с высоким коэффициентом теплопроводности (медь, алюминий, латунь)
2. Ребра целесообразно выполнять
на той поверхности, где коэффициент теплоотдачи минимальный, например, со стороны воздуха, а не воды.Определяющим критерием является коэффициент теплоотдачи, а не величина температуры
3. Нецелесообразно делать ребра большой длины (высоты)
4. Необходимо ребристую поверхность поддерживать в чистоте
Слайд 48Движущая сила тепловых процессов
разность температур взаимодействующих сред
В промышленной аппаратуре теплопередача
обычно протекает при переменной температуре теплоносителей.
Значение температуры теплоносителей изменяются вдоль
поверхности разделяющей их стенки, поэтому в расчетах используют среднюю разность температур Δtср, которая и должна войти в основное уравнение теплопередачи
Слайд 49Основное уравнение теплопередачи
количество теплоты, передаваемое в единицу времени через поверхность
при теплообмене, пропорционально средней разности температур
Таким образом, основное уравнение теплопередачи
принимает вид Q=kF Δtср
Слайд 50Схемы движения теплоносителей
Большое влияние на процесс теплообмена оказывает относительное движение
теплоносителей. В непрерывных процессах теплообмена возможны следующие варианты направления движения
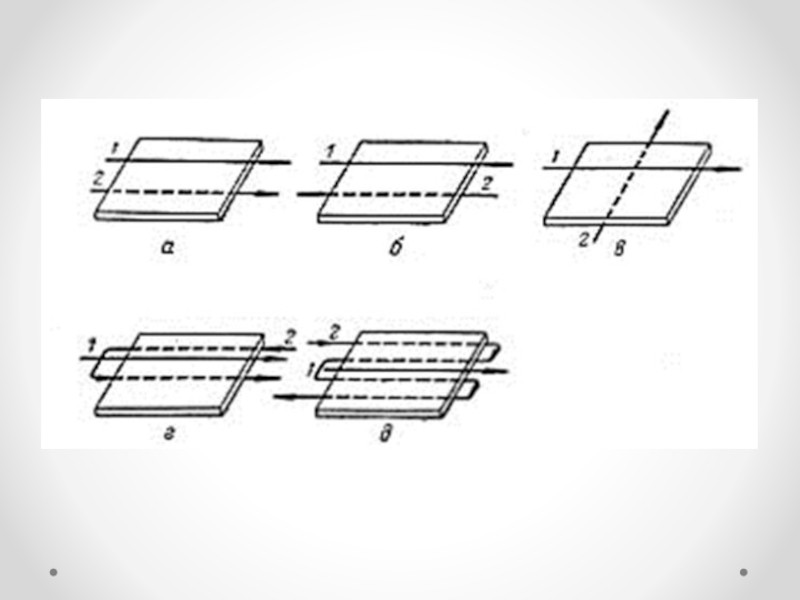
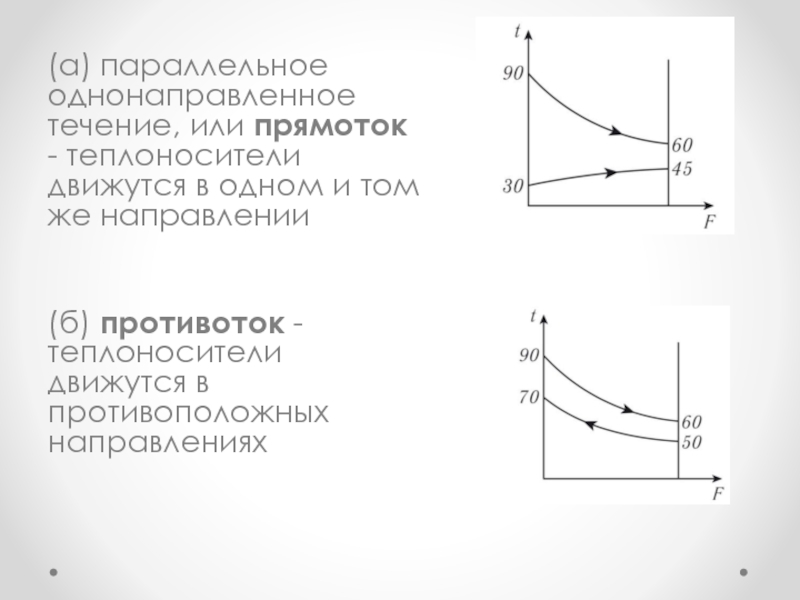
жидкостей друг относительно друга вдоль разделяющей их стенки
Слайд 52(а) параллельное однонаправленное течение, или прямоток - теплоносители движутся в
одном и том же направлении
(б) противоток - теплоносители движутся в
противоположных направлениях
Слайд 53(в)перекрестный ток , при котором теплоносители движутся взаимно перпендикулярно друг
другу
смешанный ток, при котором один из теплоносителей движется в одном
направлении, а другой - как прямотоком, так и противотоком к первому. При этом различают простой, или однократный смешанный ток (г) и многократный смешанный ток (д)
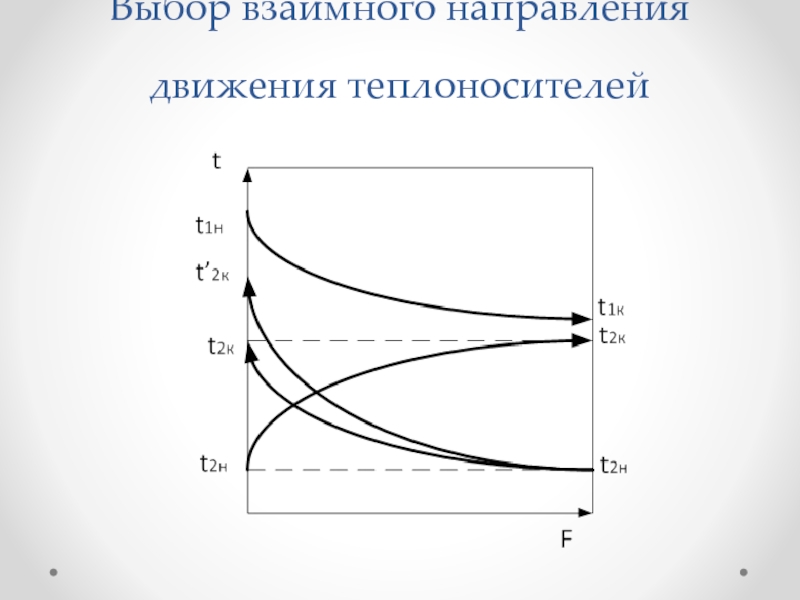
Слайд 55Для случая прямотока конечная температура менее нагретого теплоносителя (охлаждающего агента)
t2К не может превышать конечную температуру более нагретого теплоносителя t1К.
При противотоке это возможно. Для осуществления процесса должна существовать некоторая разность температур. При повышении t2К сокращается расход охлаждающего агента, т.е. противоток предпочтителен с точки зрения экономии охлаждающего агента.Если сопоставить противоток и прямоток при одинаковых начальных и конечных температурах теплоносителей, то при противотоке средняя движущая сила выше, а расход теплоносителей одинаков. Скорость теплообмена при противотоке выше, следовательно, противоток более эффективен.
Слайд 56Таким образом, противоток является более предпочтительным при проведении процессов теплообмена.
Прямоток применяют только в том случае, если он обеспечивает какие
либо технологические преимущества (например, создание более мягких условий обогрева).Если один из теплоносителей меняет свое агрегатное состояние, то взаимное направление движения теплоносителей не имеет значения.
Слайд 57Конфигурации теплообменников в зависимости от схемы движения теплоносителей
Основной характеристикой
конструкции теплообменника является тип относительного движения потоков теплоносителей, взаимная геометрия
этих течений. Ниже рассмотрены наиболее общие типы конфигураций течений.Данные конфигурации представляют собой некоторую идеализацию реальных ситуаций. На практике никогда нельзя достигнуть течения теплоносителя, совпадающего с идеальным вариантом
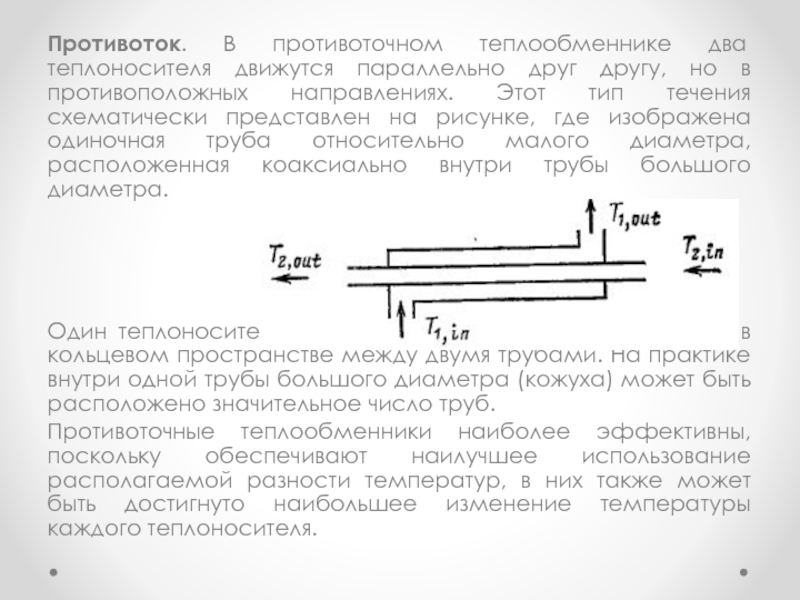
Слайд 58Противоток. В противоточном теплообменнике два теплоносителя движутся параллельно друг другу,
но в противоположных направлениях. Этот тип течения схематически представлен на
рисунке, где изображена одиночная труба относительно малого диаметра, расположенная коаксиально внутри трубы большого диаметра.Один теплоноситель течет во внутренней трубе, другой — в кольцевом пространстве между двумя трубами. На практике внутри одной трубы большого диаметра (кожуха) может быть расположено значительное число труб.
Противоточные теплообменники наиболее эффективны, поскольку обеспечивают наилучшее использование располагаемой разности температур, в них также может быть достигнуто наибольшее изменение температуры каждого теплоносителя.
Слайд 59Прямоток. В теплообменниках этого типа два теплоносителя движутся также параллельно
друг другу, но в одном и том же направлении. При
значительном изменении температуры теплоносителей располагаемая разность температур в таком теплообменнике используется плохо. В этом случае, если эффективность передачи теплоты является определяющим параметром при проектировании, такого типа теплообменники не применяют. Однако температура теплопередающей стенки в таких теплообменниках оказывается более однородной, чем в противоточных теплообменниках.
Слайд 60Перекрестный ток. В теплообменнике с перекрестным током два теплоносителя движутся
под прямым углом друг к другу.
Например, первый поток может
течь внутри труб, собранных в пучок, тогда как второй поток может двигаться в пространстве между трубами в направлении, в целом перпендикулярном оси этих труб. По своей эффективности они занимают промежуточное положение между теплообменниками с параллельным однонаправленным движением теплоносителей и противоточным теплообменником. Если же исходить из практических соображений, связанных с подачей теплоносителей к поверхностям теплообмена, то такой теплообменник сконструировать проще, чем указанные выше типы аппаратов.
Слайд 61Передача теплоты конвекцией
Конвекция (конвективная теплоотдача)
перенос тепла вследствие движения и перемешивания
макроскопических объемов газа или жидкости.
Конвекция тепла всегда сопровождается теплопроводностью.
различают
вынужденную
(принудительную) и естественную (свободную)
Слайд 62
вынужденная – жидкость или газ движутся за счет внешних для
данного процесса сил (насос, вентилятор, ветер)
естественная – обусловлена разностью плотностей
газа и жидкости в различных точках объема вследствие разности их температур в этих точках
Слайд 63Закон теплоотдачи (Ньютона-Рихмана)
Для удобства расчета теплоотдачи берут уравнение относительно простого
вида
dQ=αdF(tст-tж)dτ
Количество тепла dQ, отдаваемое за время поверхностью стенки dF,
имеющей температуру tст жидкости с температурой tж прямо пропорционально dF и разности температур tст-tж.α-коэффициент пропорциональности (теплоотдачи)
Слайд 64Коэффициент теплоотдачи
характеризует количество теплоты, которое передается
от 1 кв.м. поверхности
стенки к жидкости (или от жидкости к стенке) в течение
1 с при разности температур стенки и жидкости 1 КРазмерность – Вт/кв.м·К
Коэффициент теплоотдачи не является постоянной величиной для данного вещества или материала и зависит от следующих факторов:
Слайд 65от переменных, определяющих режим течения жидкости - скорости жидкости ω,
ее плотности ρ и вязкости μ
от тепловых свойств жидкости
(удельной теплоемкости ср, теплопроводности λ), а также от коэффициента объемного расширения βгеометрических параметров – формы и определяющих размеров стенки (для труб – их диаметр d и длина L), а также шероховатости стенки ε
α=f(ω,μ,ρ,ср,λ,β,d,L,ε)
Слайд 66Зависимость коэффициента теплоотдачи от этих факторов очень сложна и не
может быть установлена теоретическим путем.
Для определения значений α прибегают
к экспериментальным исследованиям, а опытные данные обрабатывают методом теории подобия, получая обобщенные (критериальные) уравнения для типовых случаев теплоотдачи, позволяющие рассчитывать α для условий конкретной задачи.
Слайд 67Дифференциальное уравнение конвективного теплообмена
Исходной зависимостью для обобщения данных по теплоотдаче
является общий закон распределения температур в жидкости, выражаемый дифференциальным уравнением
конвективного теплообмена.Рассмотрим уравнение теплового баланса параллелепипеда, учитывая, что тепло переносится в жидкости путем конвекции и теплопроводности.
Слайд 68Выделим в установившимся потоке жидкости элементарный параллелепипед с ребрами dx,
dy и dz.
Пусть плотность потока жидкости ρ, ее коэффициент
теплопроводности λ и удельная теплоемкость ср постоянны.Температура t жидкости изменяется вдоль граней параллелепипеда.
Проекции скорости движения ω жидкости на оси координат x, y и z составляют ωx, ωy и ωz соответственно.
Слайд 70Уравнение Фурье-Кирхгофа (дифференциальное уравнение конвективного теплообмена)
это уравнение выражает в наиболее
общем виде распределение температур в движущейся жидкости
Слайд 71Из уравнения Фурье-Кирхгофа следует, что температурное поле в движущейся жидкости
является функцией различных переменных.
Для практического использования это уравнение преобразовывают с
учетом условий однозначности, т.е. представляют в виде критериев подобия.
Слайд 72Подобные процессы
явления, принадлежащие одному и тому же классу, описывающиеся одинаковыми
по физическому содержанию и форме записи дифференциальными уравнениями
Аналогичные процессы
явления, которые описываются одинаковыми по форме записи дифференциальными
уравнениями, но различны по своему физическому содержанию
Слайд 73Общие условия подобия физических процессов (по Кирпичеву – Гухману)
1. Подобные
процессы должны быть качественно одинаковыми, т. е. они должны иметь
одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями2. Условия однозначности подобных процессов должны быть одинаковы во всем, кроме численных значений постоянных, содержащихся в этих условиях
3. Одноименные определяющие критерии подобных процессов должны иметь одинаковую численную величину
Слайд 74 С помощью теории подобия размерные физические величины объединяются в безразмерные
комплексы, число которых комплексов будет меньше числа величин, из которых
составлены эти комплексы. Полученные безразмерные комплексы рассматриваются как новые переменные.При введении в уравнения безразмерных комплексов число величин под знаком функции формально сокращается, что упрощает исследование физических процессов. Кроме того, новые безразмерные переменные отражают влияние не только отдельных одиночных факторов, но и их совокупности, что позволяет легче определить физические связи в исследуемом процессе.
Слайд 75 Теория подобия устанавливает условия, при которых результаты лабораторных исследований можно
распространить на другие явления, подобные рассматриваемому. Ввиду этого теория подобия
является прежде всего теоретической базой эксперимента и облегчает анализ процесса, а также описание полученных результатов, хотя с ее помощью вид искомой функции не может быть определен.
Слайд 76К ним относятся:
число Рейнольдса
характеризует соотношение между инерционными силами
и силами трения в подобных потокам
Re=vlρ/μ
v – скорость движения жидкости,
м/сl – характерный линейный размер, м
ρ – плотность жидкости, кг/куб.м
μ – динамическая вязкость жидкости, Па·с
Слайд 772) число Нуссельта
характеризует интенсивность теплообмена на границе между стенкой и
средой
Nu=αl/λ
α – коэффициент теплоотдачи, Вт/кв.м·К
λ – коэффициент теплопроводности среды, Вт/м·К
Слайд 783) число Пекле
характеризует соотношение между теплотой, переносимой путем конвекции, и
теплопроводностью
Pe=vl/a
a - коэффициент температуропроводности, кв.м/с
Слайд 794) число Прандтля
характеризует подобие физических свойств теплоносителей в процессах конвективного
теплообмена
Pr=cμ/λ
c – удельная теплоемкость жидкости, Дж/кг·К
