Слайд 1Тени от трехмерных геометрических объектов
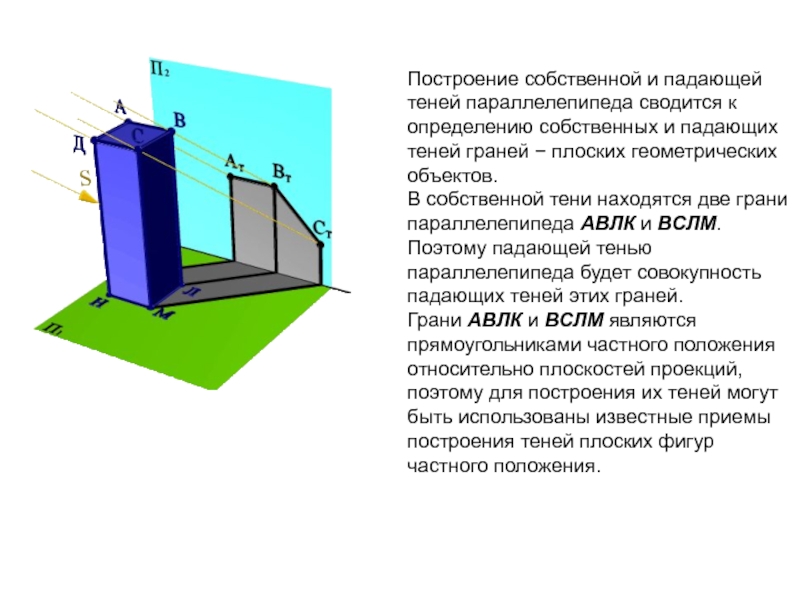
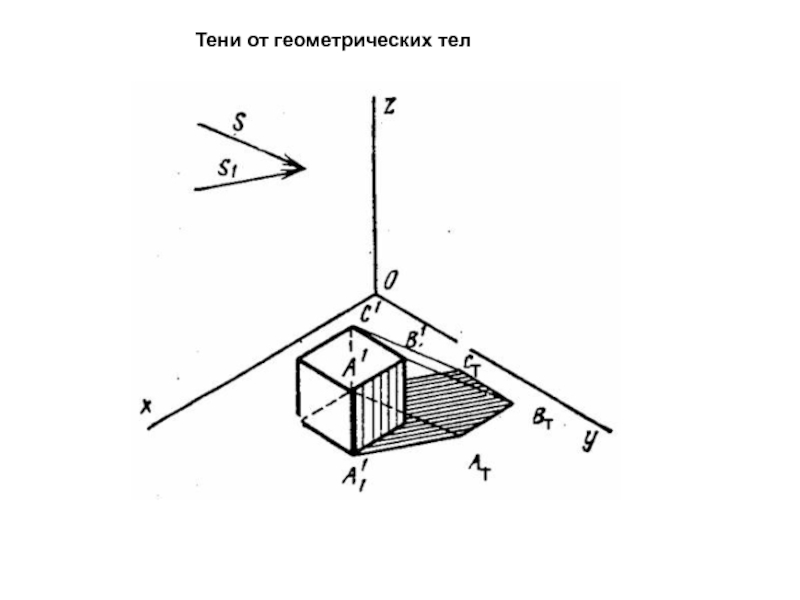
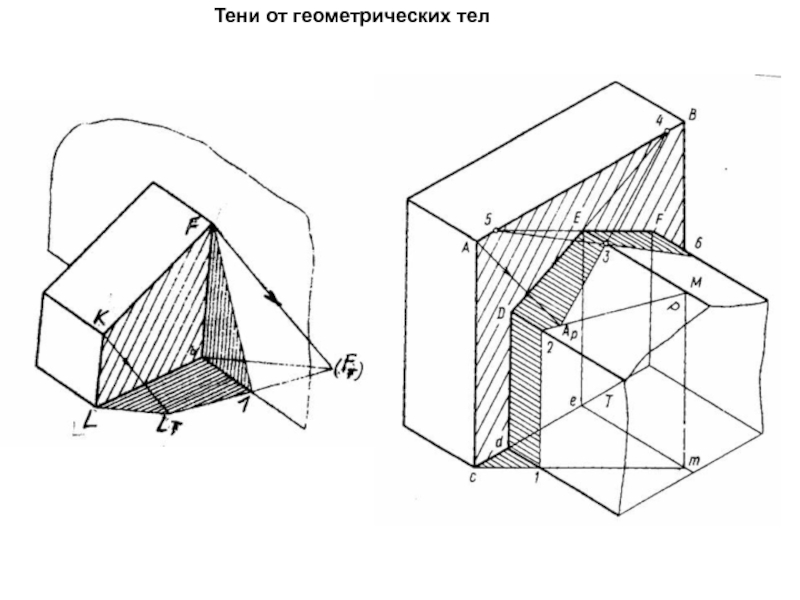
Слайд 2Построение собственной и падающей теней параллелепипеда сводится к определению собственных
и падающих теней граней − плоских геометрических объектов.
В собственной
тени находятся две грани параллелепипеда АВЛК и ВСЛМ. Поэтому падающей тенью параллелепипеда будет совокупность падающих теней этих граней.
Грани АВЛК и ВСЛМ являются прямоугольниками частного положения относительно плоскостей проекций, поэтому для построения их теней могут быть использованы известные приемы построения теней плоских фигур частного положения.
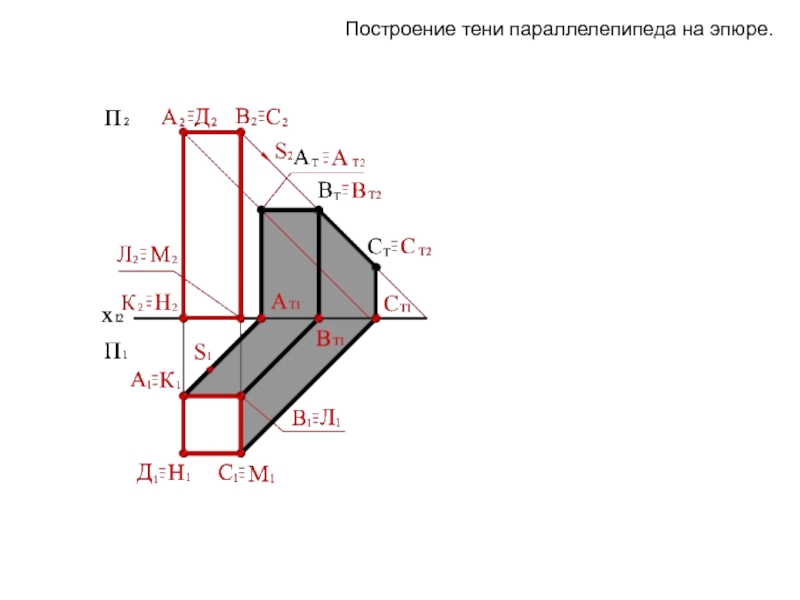
Слайд 3Построение тени параллелепипеда на эпюре.
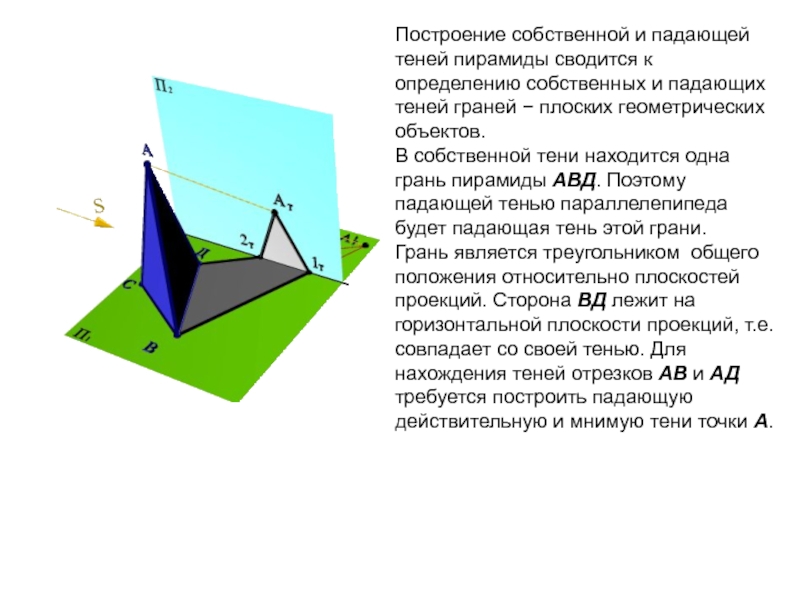
Слайд 4Построение собственной и падающей теней пирамиды сводится к определению собственных
и падающих теней граней − плоских геометрических объектов.
В собственной
тени находится одна грань пирамиды АВД. Поэтому падающей тенью параллелепипеда будет падающая тень этой грани.
Грань является треугольником общего положения относительно плоскостей проекций. Сторона ВД лежит на горизонтальной плоскости проекций, т.е. совпадает со своей тенью. Для нахождения теней отрезков АВ и АД требуется построить падающую действительную и мнимую тени точки А.
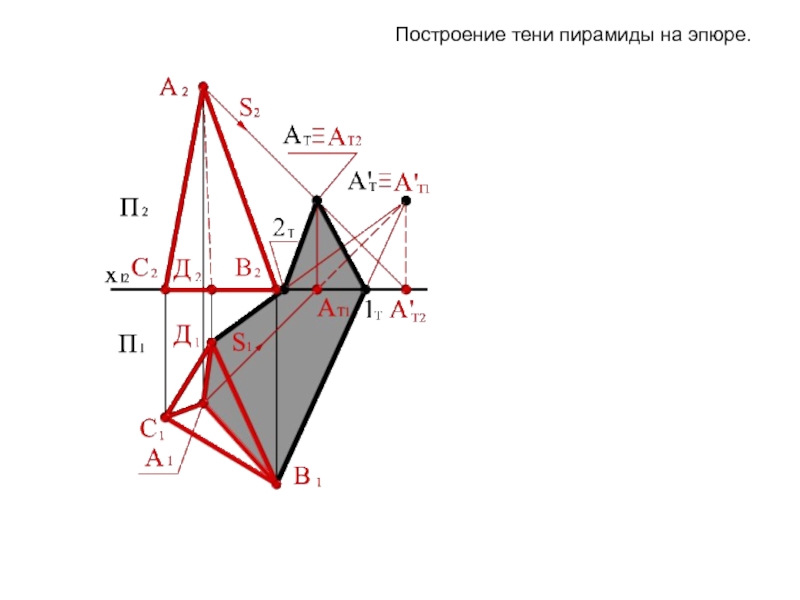
Слайд 5Построение тени пирамиды на эпюре.
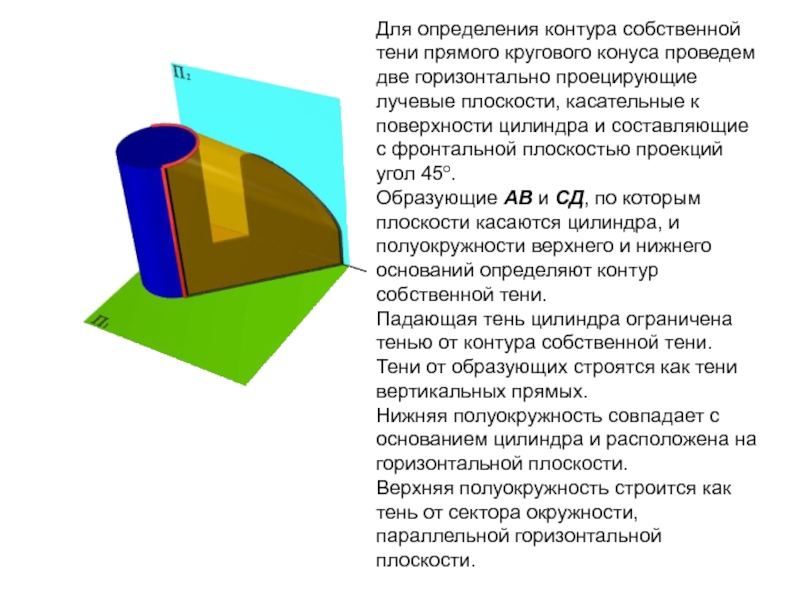
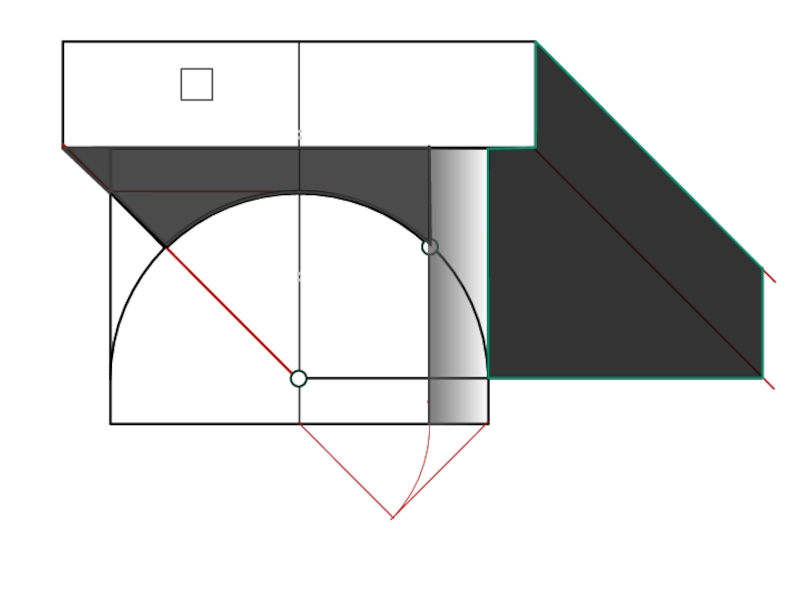
Слайд 6Для определения контура собственной тени прямого кругового конуса проведем две
горизонтально проецирующие лучевые плоскости, касательные к поверхности цилиндра и составляющие
с фронтальной плоскостью проекций угол 45о.
Образующие АВ и СД, по которым плоскости касаются цилиндра, и полуокружности верхнего и нижнего оснований определяют контур собственной тени.
Падающая тень цилиндра ограничена тенью от контура собственной тени.
Тени от образующих строятся как тени вертикальных прямых.
Нижняя полуокружность совпадает с основанием цилиндра и расположена на горизонтальной плоскости.
Верхняя полуокружность строится как тень от сектора окружности, параллельной горизонтальной плоскости.
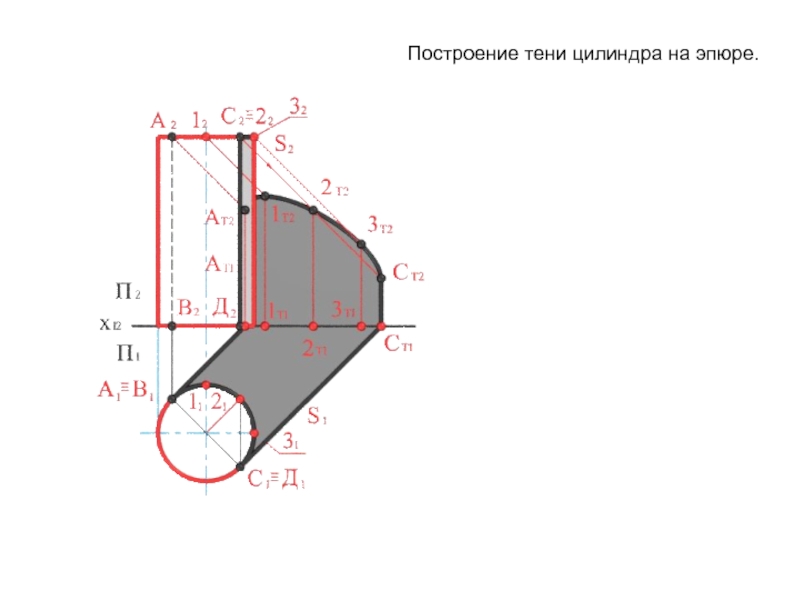
Слайд 7Построение тени цилиндра на эпюре.
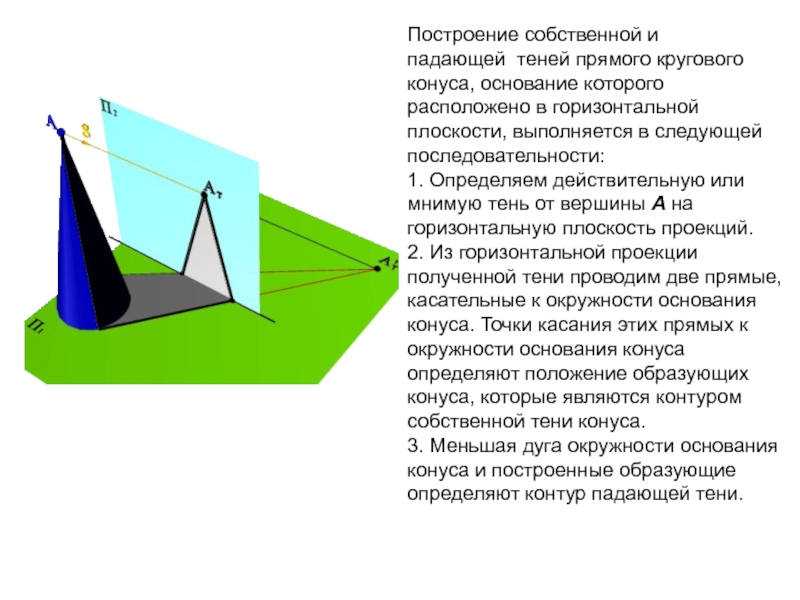
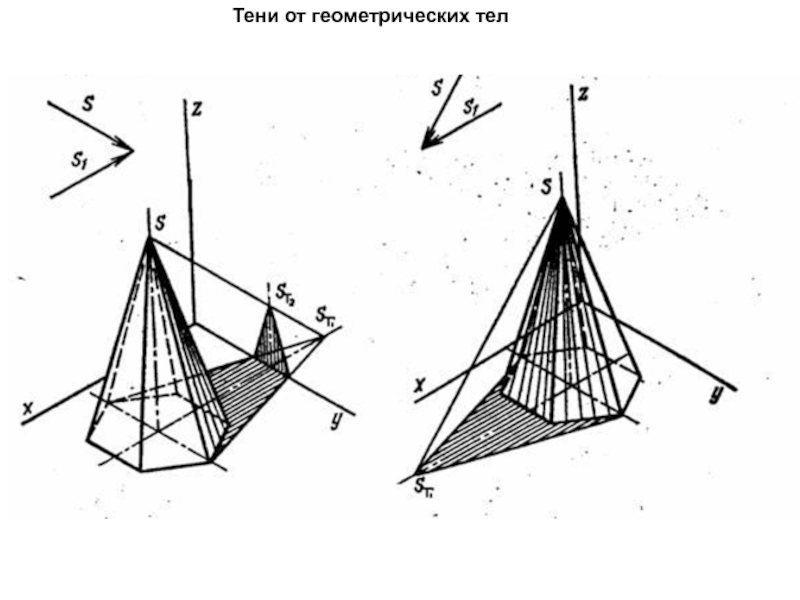
Слайд 8Построение собственной и падающей теней прямого кругового конуса, основание которого
расположено в горизонтальной плоскости, выполняется в следующей последовательности:
1. Определяем действительную
или мнимую тень от вершины А на горизонтальную плоскость проекций.
2. Из горизонтальной проекции полученной тени проводим две прямые, касательные к окружности основания конуса. Точки касания этих прямых к окружности основания конуса определяют положение образующих конуса, которые являются контуром собственной тени конуса.
3. Меньшая дуга окружности основания конуса и построенные образующие определяют контур падающей тени.
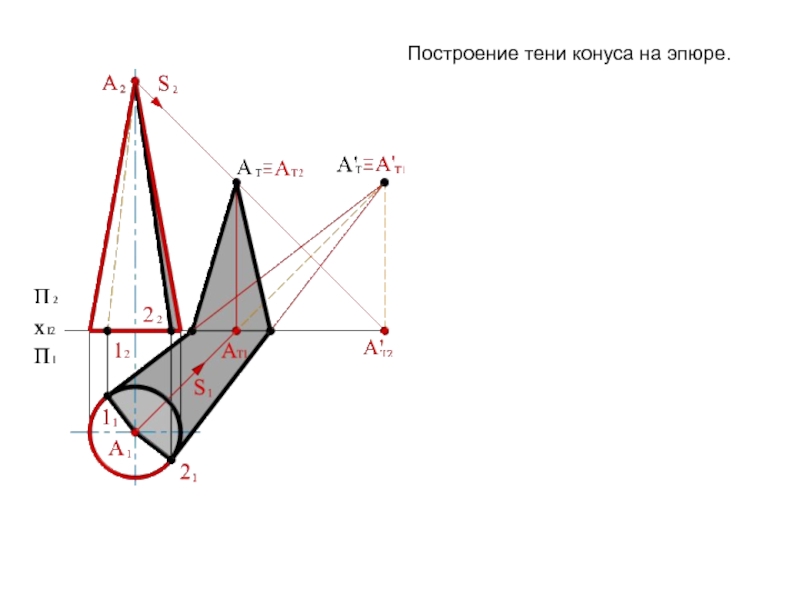
Слайд 9Построение тени конуса на эпюре.
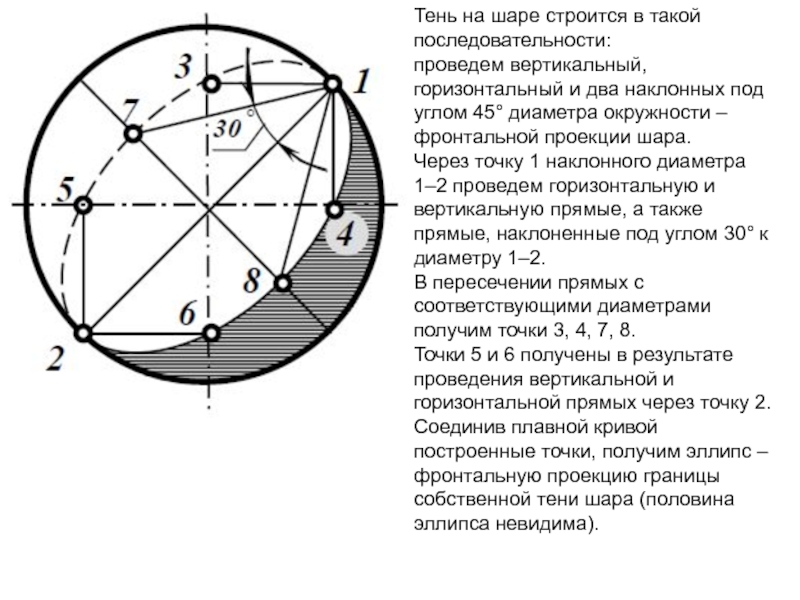
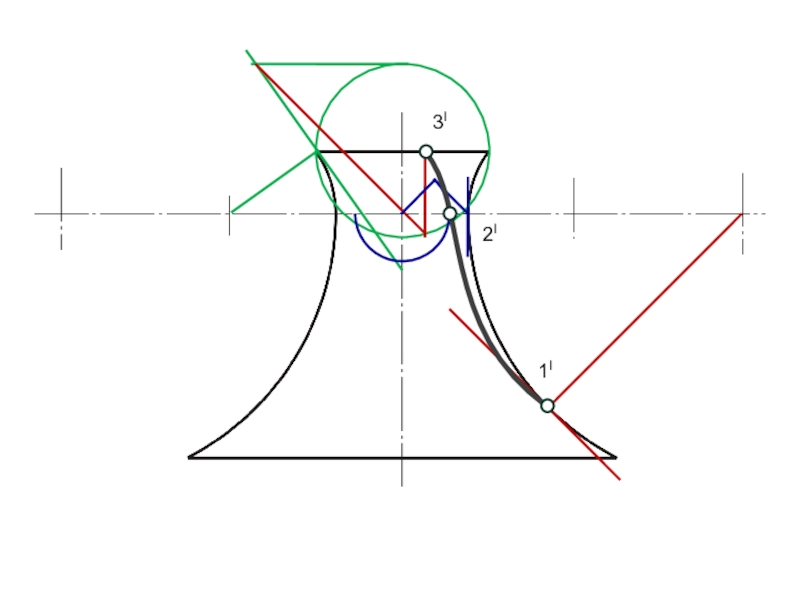
Слайд 10Тень на шаре строится в такой последовательности:
проведем вертикальный, горизонтальный
и два наклонных под углом 45° диаметра окружности – фронтальной
проекции шара.
Через точку 1 наклонного диаметра 1–2 проведем горизонтальную и вертикальную прямые, а также прямые, наклоненные под углом 30° к диаметру 1–2.
В пересечении прямых с соответствующими диаметрами получим точки 3, 4, 7, 8.
Точки 5 и 6 получены в результате проведения вертикальной и горизонтальной прямых через точку 2.
Соединив плавной кривой построенные точки, получим эллипс – фронтальную проекцию границы собственной тени шара (половина эллипса невидима).
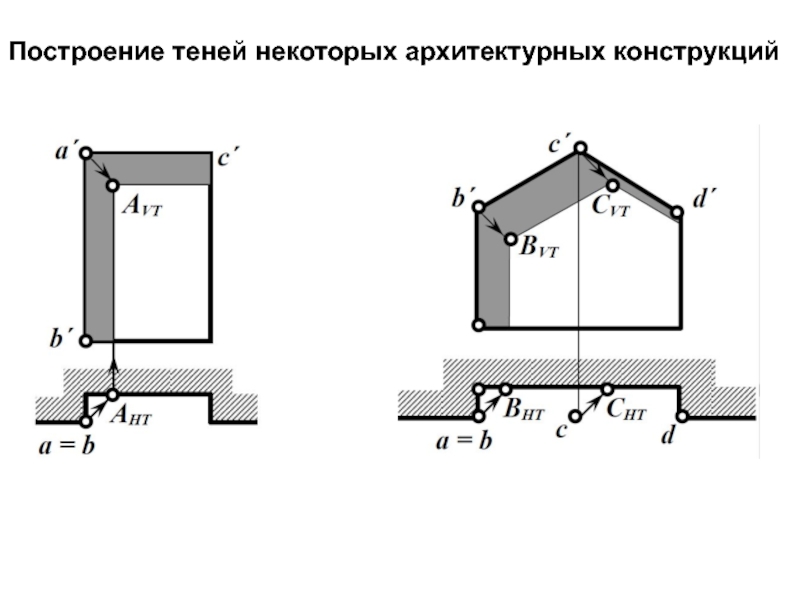
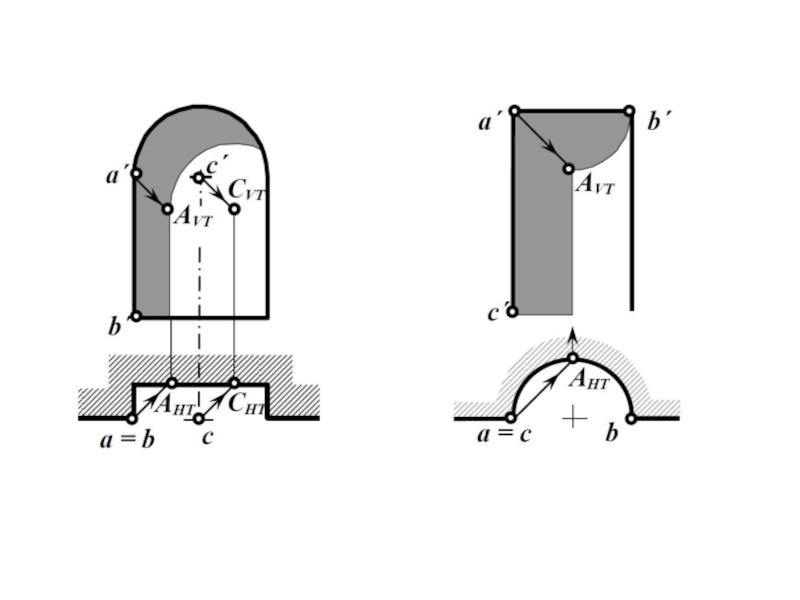
Слайд 11Построение теней некоторых архитектурных конструкций
Слайд 13Рис. 7
Рис.7
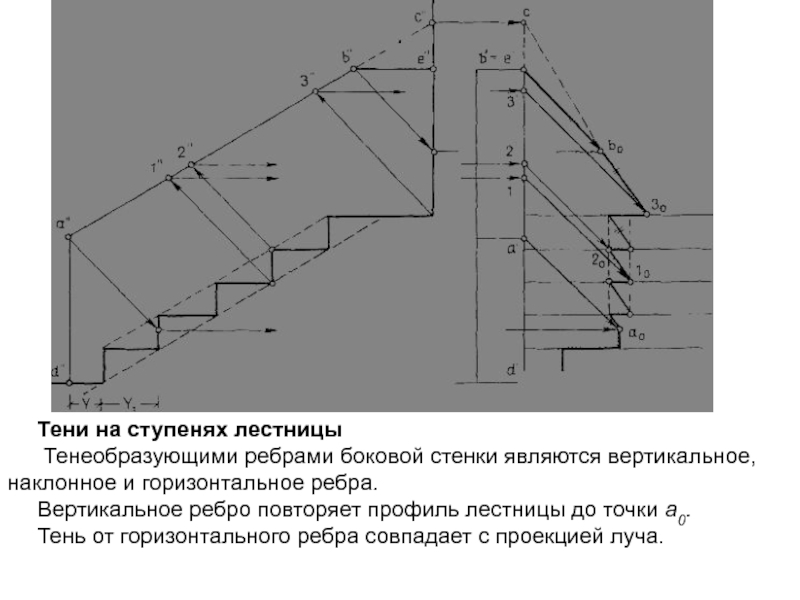
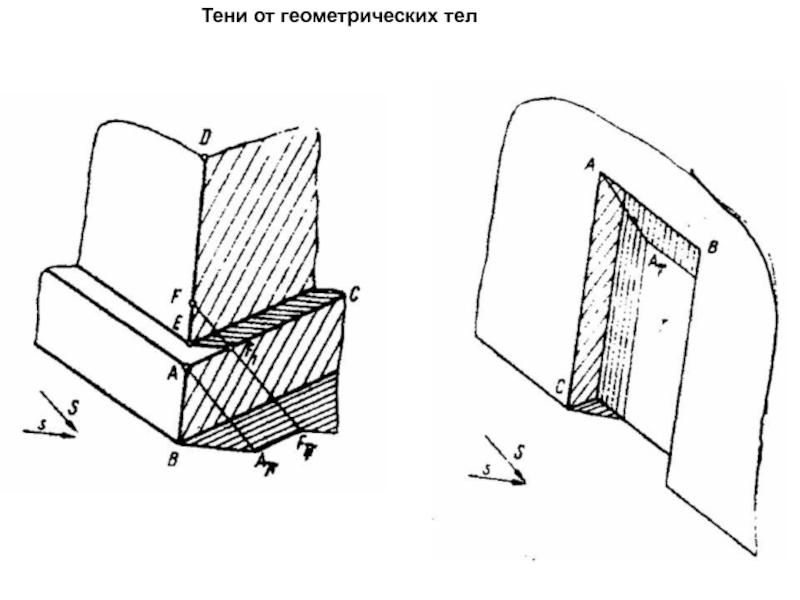
Тени на ступенях лестницы
Тенеобразующими ребрами боковой стенки
являются вертикальное, наклонное и горизонтальное ребра.
Вертикальное ребро повторяет профиль лестницы
до точки а0.
Тень от горизонтального ребра совпадает с проекцией луча.
Слайд 14Рис. 7
Рис.7
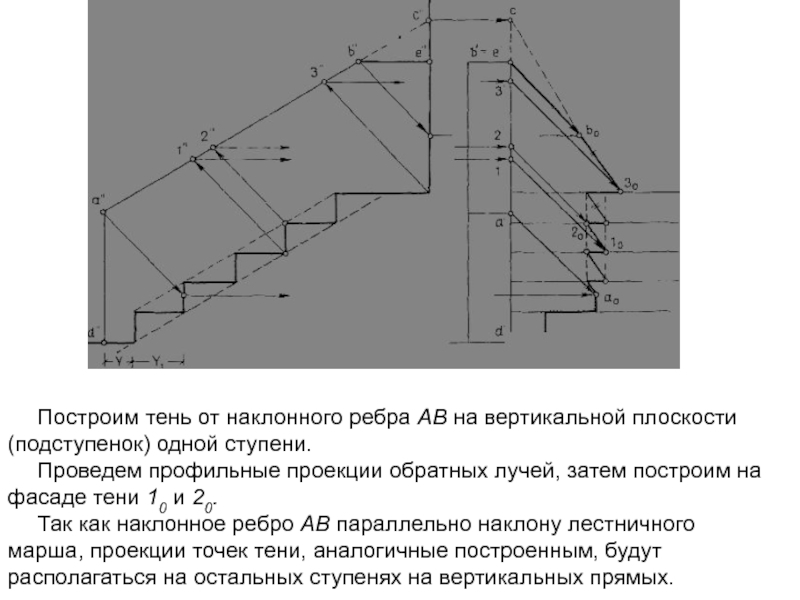
Построим тень от наклонного ребра АВ на вертикальной плоскости
(подступенок) одной ступени.
Проведем профильные проекции обратных лучей, затем построим на
фасаде тени 10 и 20.
Так как наклонное ребро АВ параллельно наклону лестничного марша, проекции точек тени, аналогичные построенным, будут располагаться на остальных ступенях на вертикальных прямых.
Слайд 15ТЕНИ КОМБИНИРОВАННЫХ ПОВЕРХНОСТЕЙ
Слайд 1612
22
02
Ат2
А2
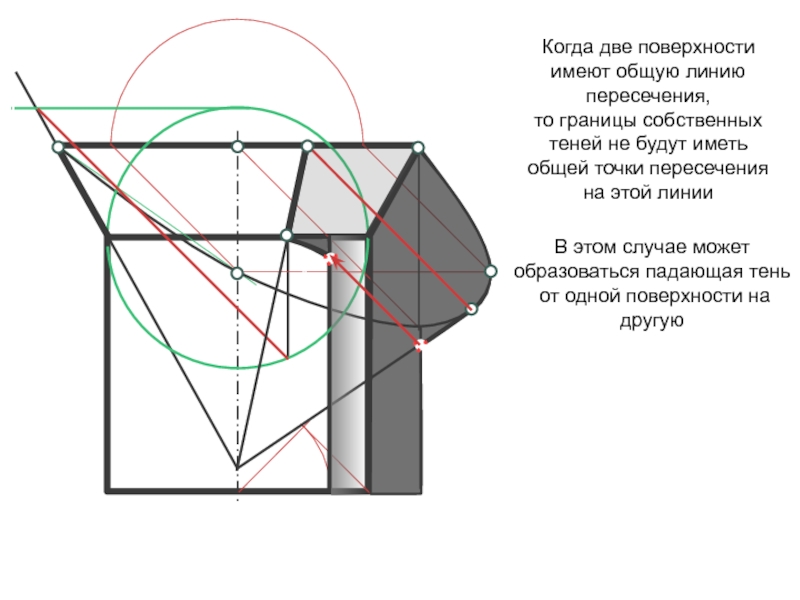
Когда две поверхности имеют общую линию пересечения,
то границы собственных
теней не будут иметь общей точки пересечения на этой линии
В
этом случае может образоваться падающая тень
от одной поверхности на другую
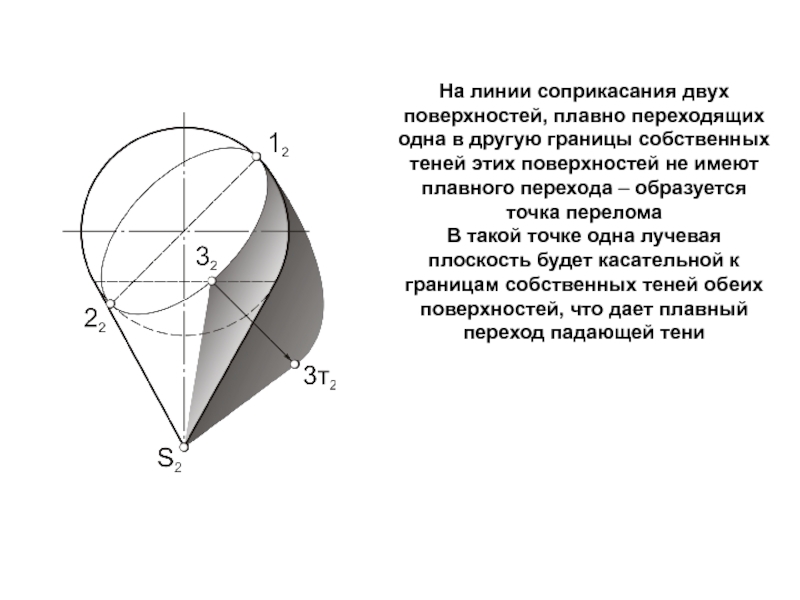
Слайд 17На линии соприкасания двух поверхностей, плавно переходящих одна в другую
границы собственных теней этих поверхностей не имеют плавного перехода –
образуется точка перелома
В такой точке одна лучевая плоскость будет касательной к границам собственных теней обеих поверхностей, что дает плавный переход падающей тени
Слайд 19
Конус
Рис.1
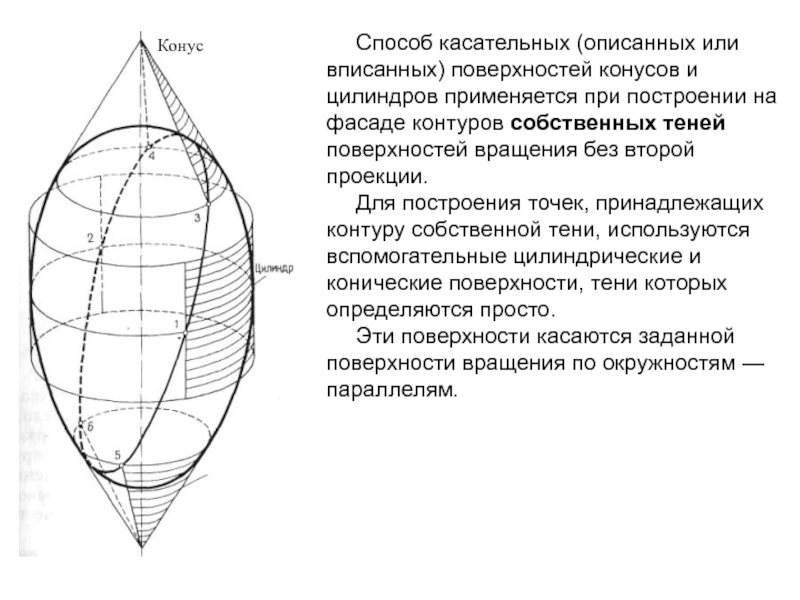
Способ касательных (описанных или вписанных) поверхностей конусов и цилиндров применяется
при построении на фасаде контуров собственных теней поверхностей вращения без
второй проекции.
Для построения точек, принадлежащих контуру собственной тени, используются вспомогательные цилиндрические и конические поверхности, тени которых определяются просто.
Эти поверхности касаются заданной поверхности вращения по окружностям — параллелям.
Слайд 20
Сначала применяют вспомогательные цилиндрические поверхности, которые касаются поверхности вращения по
экватору или горловине, затем применяют касательные конусы, соосные с данной
поверхностью.
После этого определяют теневые образующие вспомогательных поверхностей и отмечают точки их соприкосновения с соответствующими параллелями данной поверхности. Эти точки принадлежат контуру собственной тени поверхности вращения. Полученные точки тени соединяют плавной кривой.
При построении контура собственной тени прежде всего необходимо построить характерные точки контура — точки тени, лежащие на фронтальном и профильном очерках поверхности (точки видимости), а также высшую и низшую точки контура тени. Первые две точки определяют с помощью касательных конусов с углом наклона образующей 45°, а вторые две точки — с помощью конусов с углом наклона образующей 35°.
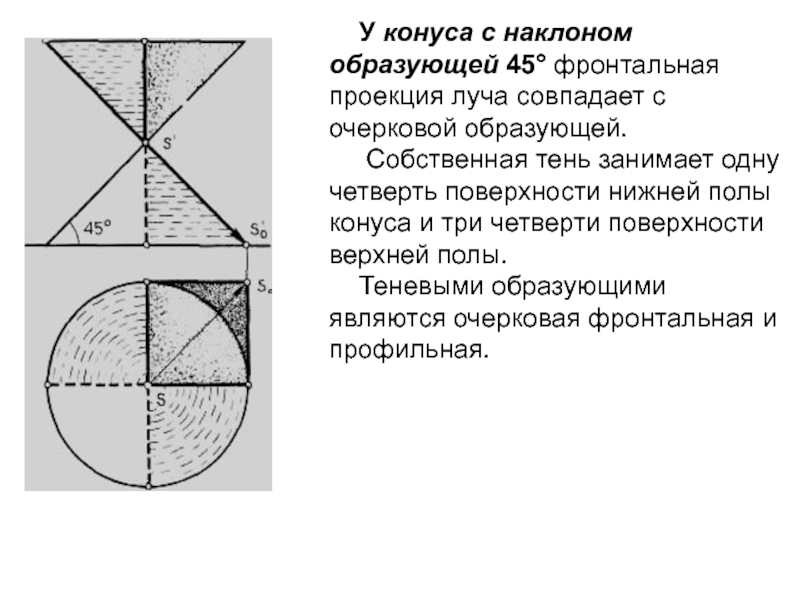
Слайд 21У конуса с наклоном образующей 45° фронтальная проекция луча совпадает
с очерковой образующей.
Собственная тень занимает одну четверть поверхности нижней
полы конуса и три четверти поверхности верхней полы.
Теневыми образующими являются очерковая фронтальная и профильная.
Рис.2
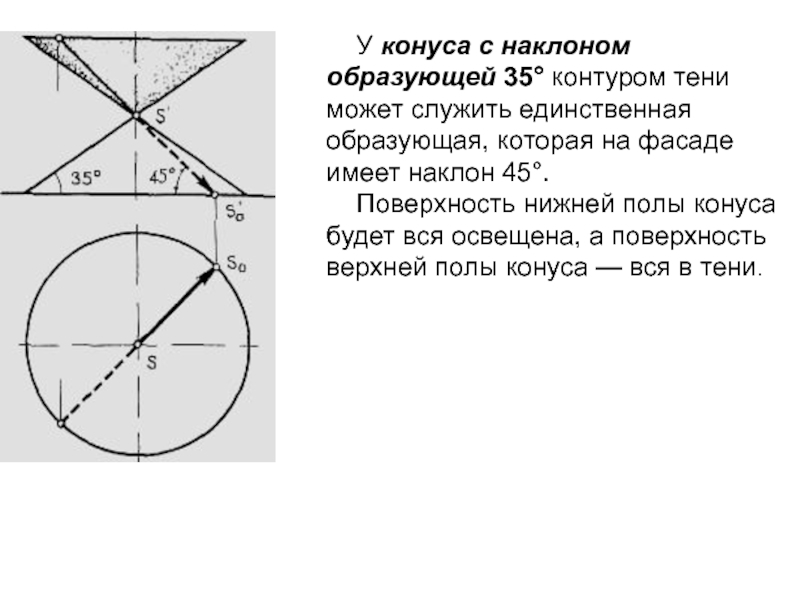
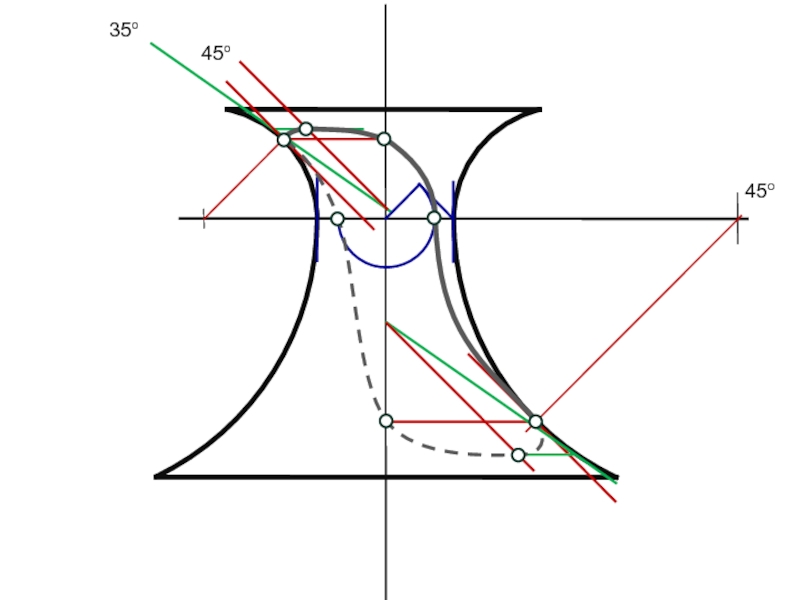
Слайд 22У конуса с наклоном образующей 35° контуром тени может служить
единственная образующая, которая на фасаде имеет наклон 45°.
Поверхность нижней
полы конуса будет вся освещена, а поверхность верхней полы конуса — вся в тени.
Рис.3
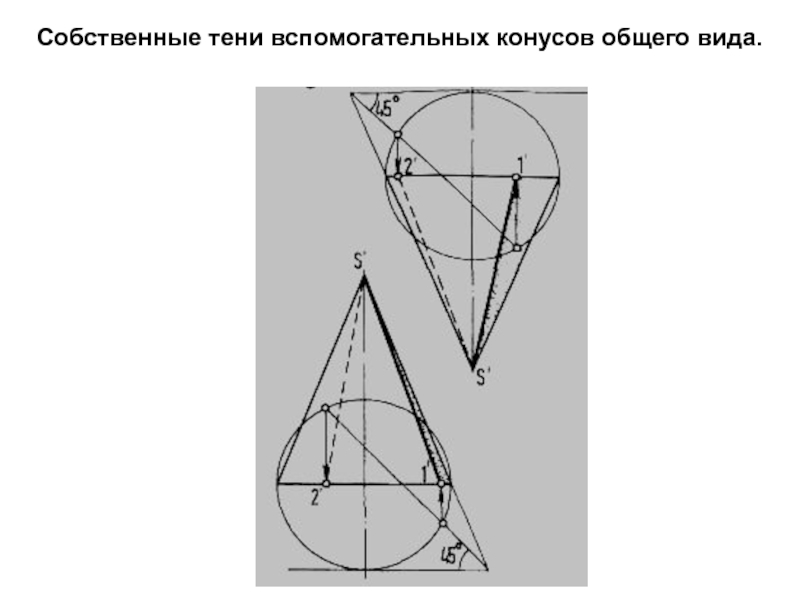
Слайд 23Собственные тени вспомогательных конусов общего вида.
Рис.4а
Слайд 24
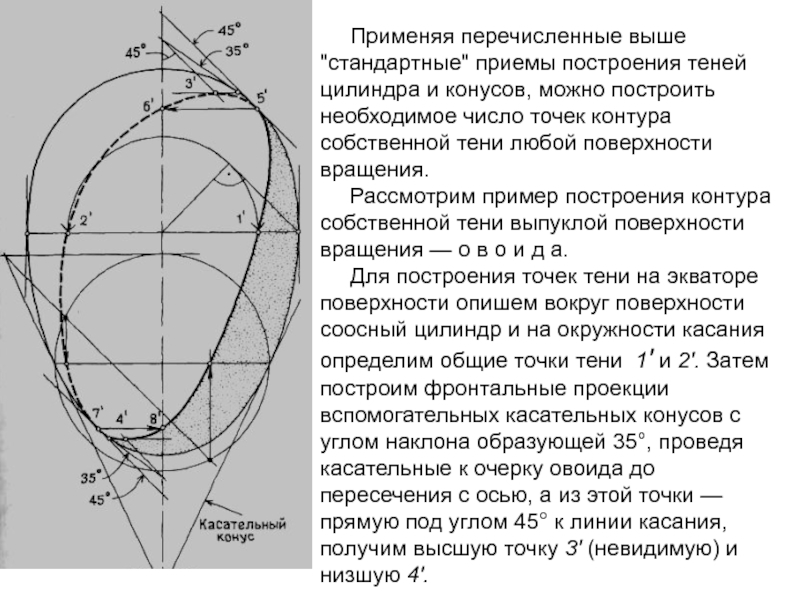
Применяя перечисленные выше "стандартные" приемы построения теней цилиндра и конусов,
можно построить необходимое число точек контура собственной тени любой поверхности
вращения.
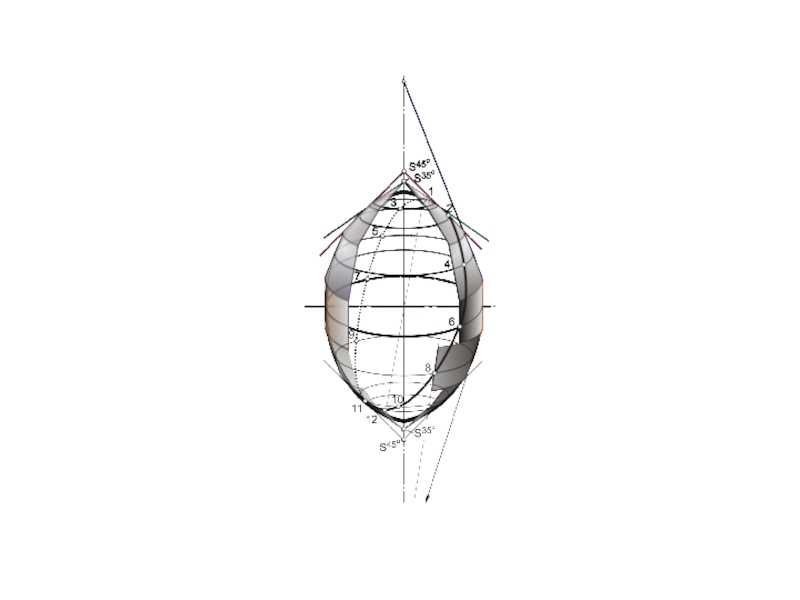
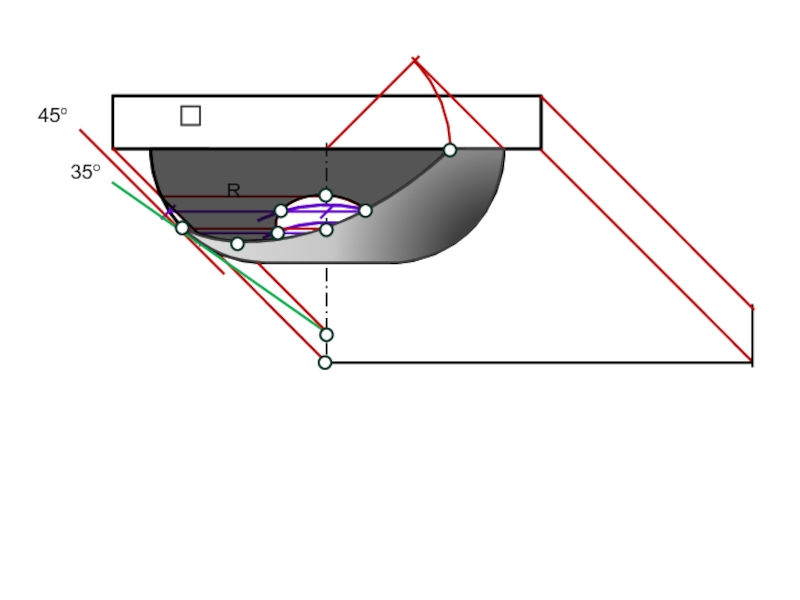
Рассмотрим пример построения контура собственной тени выпуклой поверхности вращения — о в о и д а.
Для построения точек тени на экваторе поверхности опишем вокруг поверхности соосный цилиндр и на окружности касания определим общие точки тени 1' и 2'. Затем построим фронтальные проекции вспомогательных касательных конусов с углом наклона образующей 35°, проведя касательные к очерку овоида до пересечения с осью, а из этой точки — прямую под углом 45° к линии касания, получим высшую точку 3' (невидимую) и низшую 4'.
Слайд 25
Рис.6
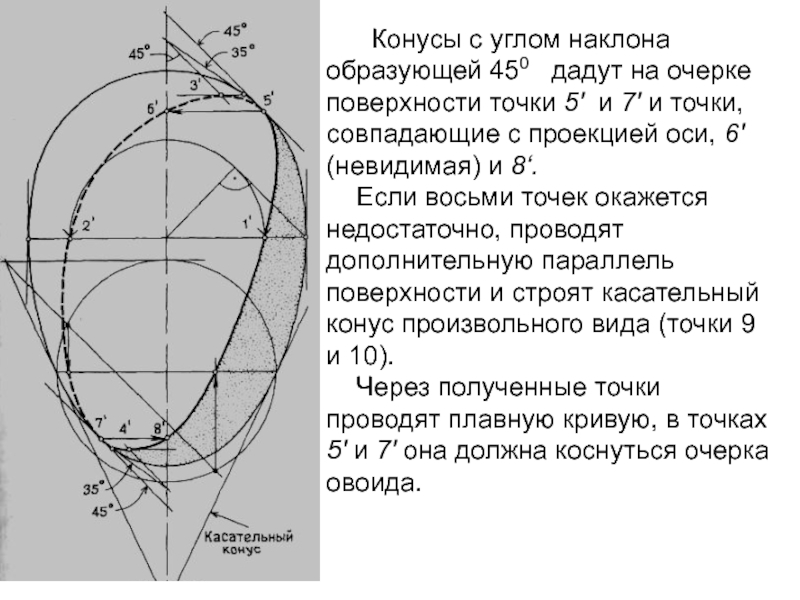
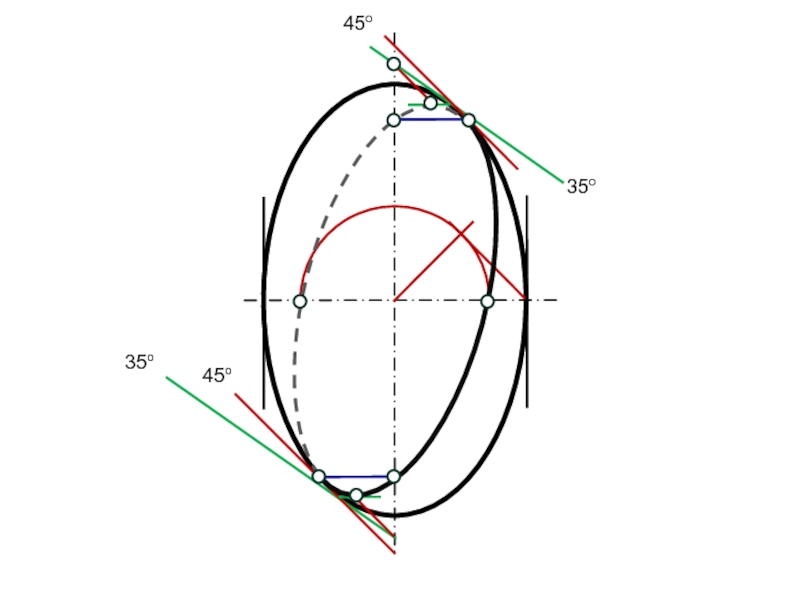
Конусы с углом наклона образующей 450 дадут на
очерке поверхности точки 5' и 7' и точки, совпадающие с
проекцией оси, 6' (невидимая) и 8‘.
Если восьми точек окажется недостаточно, проводят дополнительную параллель поверхности и строят касательный конус произвольного вида (точки 9 и 10).
Через полученные точки проводят плавную кривую, в точках 5' и 7' она должна коснуться очерка овоида.
Рис.5
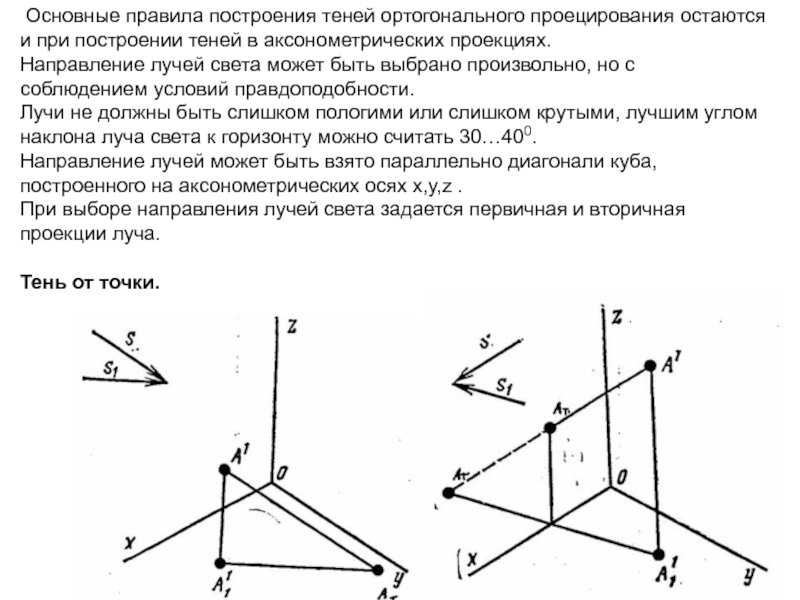
Слайд 34 Основные правила построения теней ортогонального проецирования остаются и при построении
теней в аксонометрических проекциях.
Направление лучей света может быть выбрано
произвольно, но с соблюдением условий правдоподобности.
Лучи не должны быть слишком пологими или слишком крутыми, лучшим углом наклона луча света к горизонту можно считать 30…400.
Направление лучей может быть взято параллельно диагонали куба, построенного на аксонометрических осях x,y,z .
При выборе направления лучей света задается первичная и вторичная проекции луча.
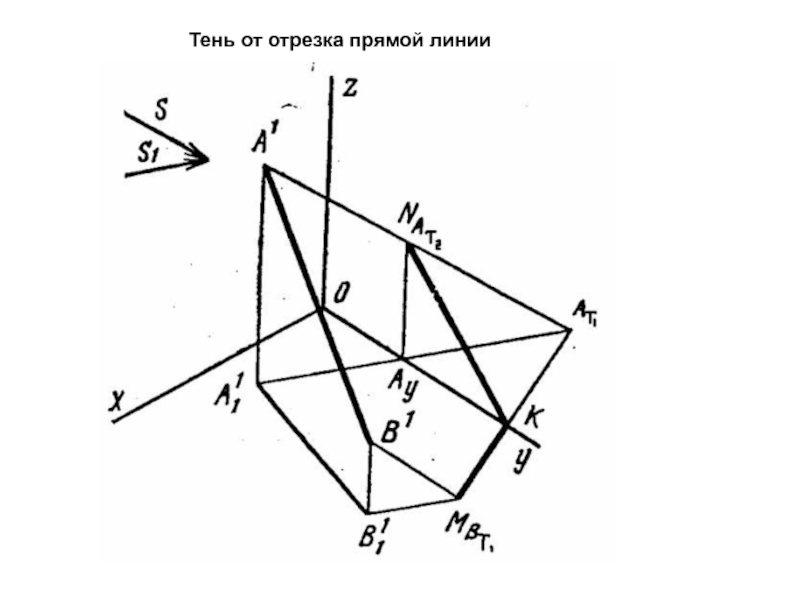
Тень от точки.
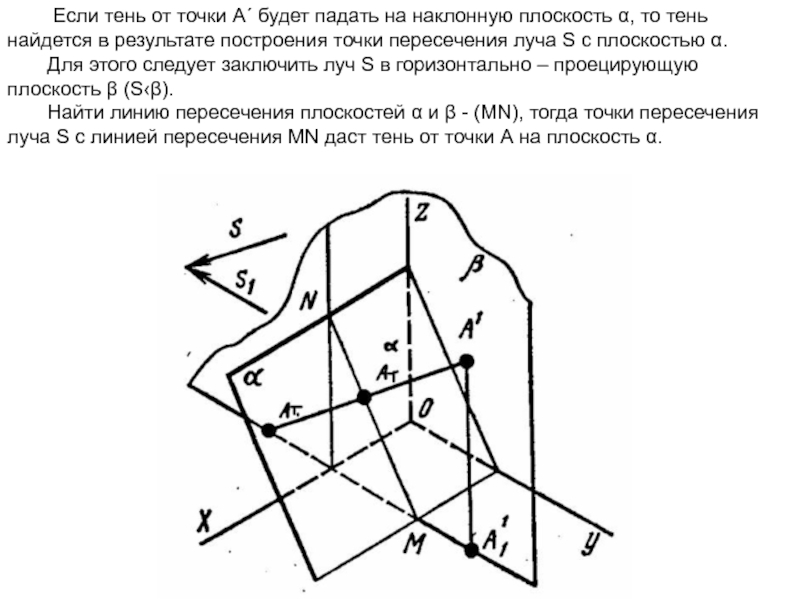
Слайд 35 Если тень от точки А´ будет падать на наклонную плоскость
α, то тень найдется в результате построения точки пересечения луча
S с плоскостью α.
Для этого следует заключить луч S в горизонтально – проецирующую плоскость β (S‹β).
Найти линию пересечения плоскостей α и β - (МN), тогда точки пересечения луча S с линией пересечения МN даст тень от точки А на плоскость α.
Слайд 42Рис. 2
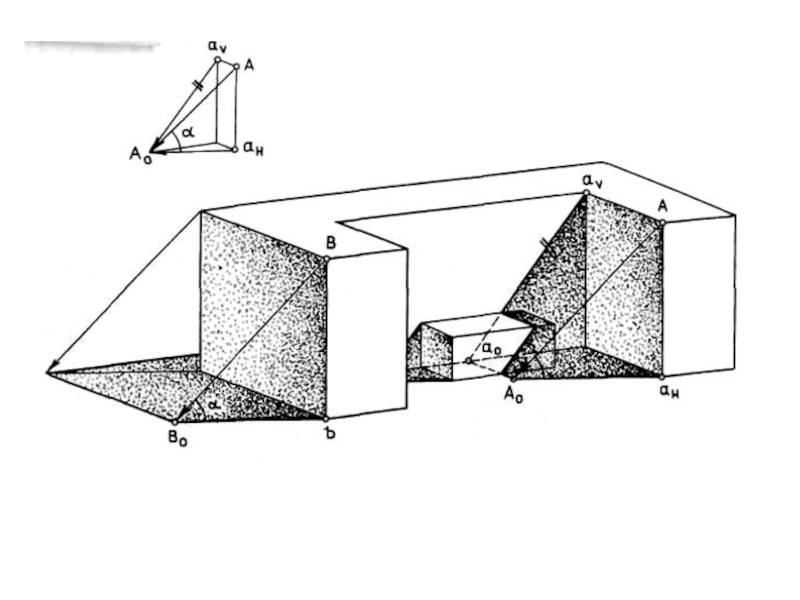
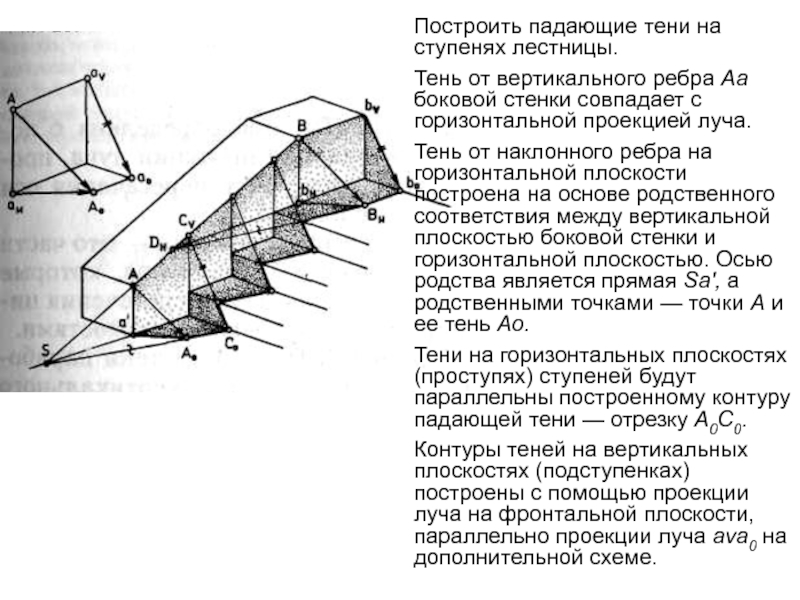
Построить падающие тени на ступенях лестницы.
Тень от вертикального ребра
Аа боковой стенки совпадает с горизонтальной проекцией луча.
Тень от
наклонного ребра на горизонтальной плоскости построена на основе родственного соответствия между вертикальной плоскостью боковой стенки и горизонтальной плоскостью. Осью родства является прямая Sa', а родственными точками — точки А и ее тень Ао.
Тени на горизонтальных плоскостях (проступях) ступеней будут параллельны построенному контуру падающей тени — отрезку А0С0.
Контуры теней на вертикальных плоскостях (подступенках) построены с помощью проекции луча на фронтальной плоскости, параллельно проекции луча ava0 на дополнительной схеме.
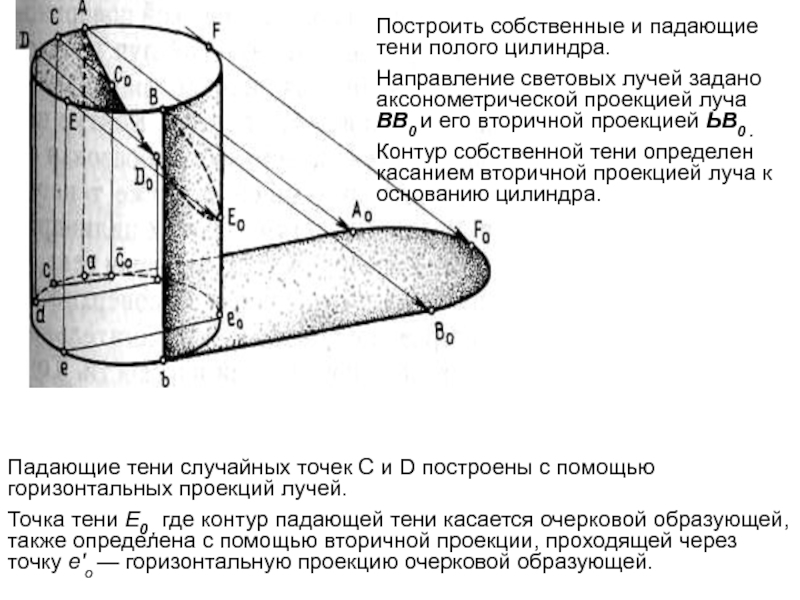
Слайд 43Построить собственные и падающие тени полого цилиндра.
Направление световых лучей задано
аксонометрической проекцией луча ВВ0 и его вторичной проекцией ЬВ0 .
Контур
собственной тени определен касанием вторичной проекцией луча к основанию цилиндра.
Падающие тени случайных точек С и D построены с помощью горизонтальных проекций лучей.
Точка тени Е0 , где контур падающей тени касается очерковой образующей, также определена с помощью вторичной проекции, проходящей через точку е'о — горизонтальную проекцию очерковой образующей.
Слайд 44Рис.4
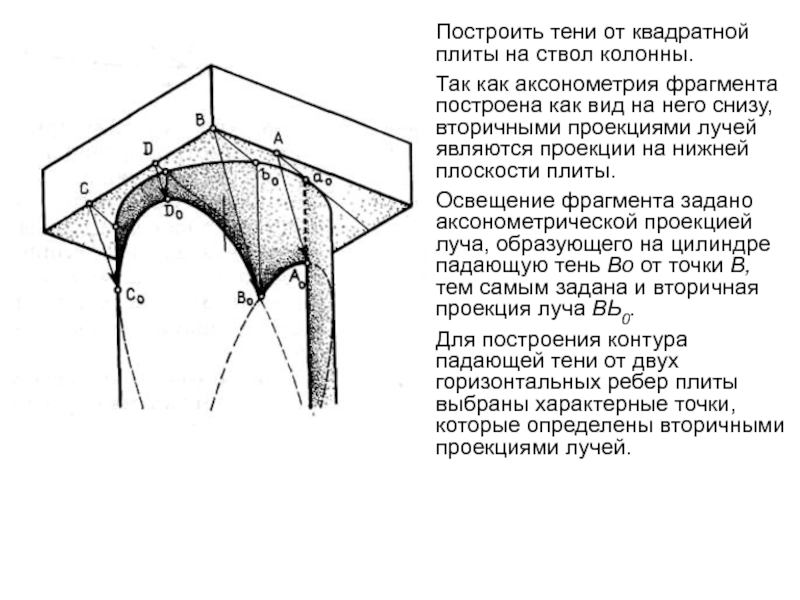
Построить тени от квадратной плиты на ствол колонны.
Так как
аксонометрия фрагмента построена как вид на него снизу, вторичными проекциями
лучей являются проекции на нижней плоскости плиты.
Освещение фрагмента задано аксонометрической проекцией луча, образующего на цилиндре падающую тень Во от точки В, тем самым задана и вторичная проекция луча ВЬ0.
Для построения контура падающей тени от двух горизонтальных ребер плиты выбраны характерные точки, которые определены вторичными проекциями лучей.
Слайд 45Рис.4
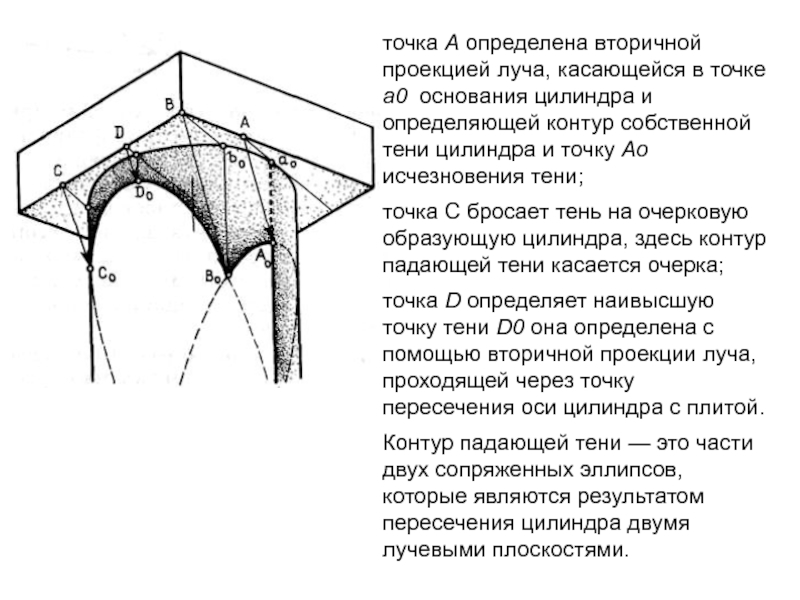
точка А определена вторичной проекцией луча, касающейся в точке а0
основания цилиндра и определяющей контур собственной тени цилиндра и точку
Ао исчезновения тени;
точка С бросает тень на очерковую образующую цилиндра, здесь контур падающей тени касается очерка;
точка D определяет наивысшую точку тени D0 она определена с помощью вторичной проекции луча, проходящей через точку пересечения оси цилиндра с плитой.
Контур падающей тени — это части двух сопряженных эллипсов, которые являются результатом пересечения цилиндра двумя лучевыми плоскостями.