ПОТЕНЦИАЛОМ
5.1. Теорема о циркуляции вектора
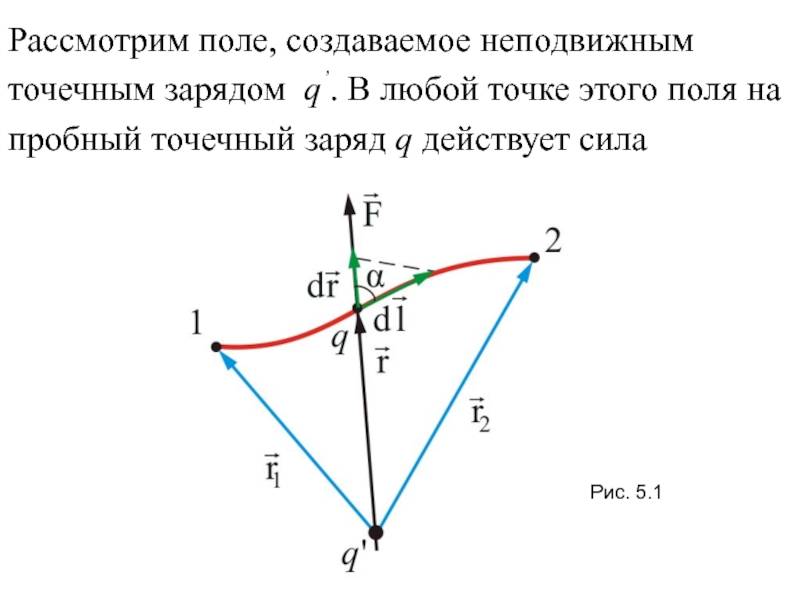
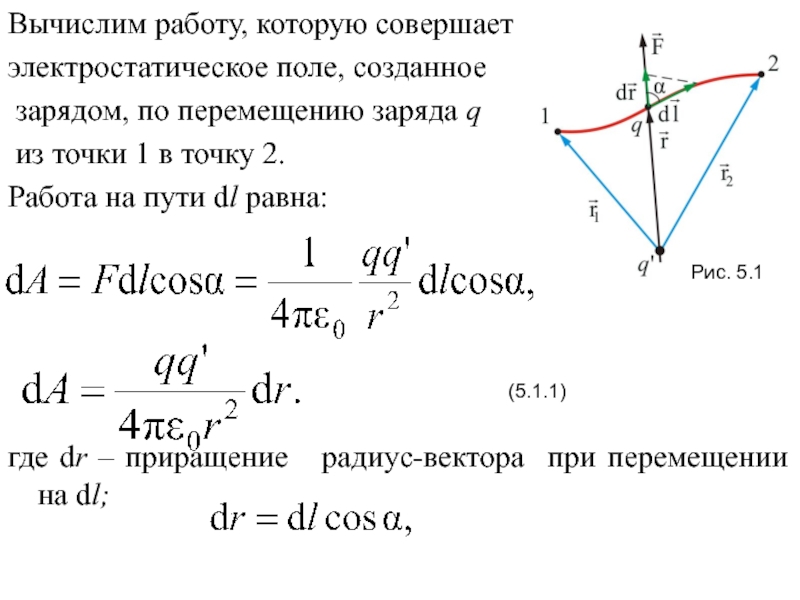
5.2. Работа сил электростатического поля.
Потенциальная энергия5.3. Потенциал. Разность потенциалов
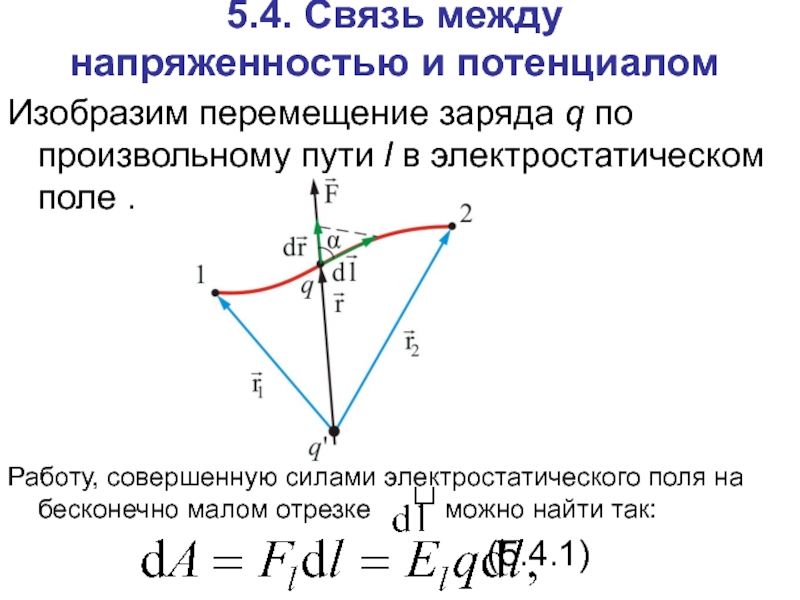
5.4. Связь между напряженностью и потенциалом
5.5. Силовые линии и эквипотенциальные поверхности
5.6. Расчет потенциалов простейших
электростатических полей