Слайд 1
«Теорема о трех перпендикулярах»
Слайд 21. Угол между прямыми равен 90˚. Как называются такие прямые?
Ответ: перпендикулярные.
2. Верно
ли утверждение: «прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой
прямой, лежащей этой плоскости»
Ответ: да.
3. Сформулируйте признак перпендикулярности прямой и плоскости.
Ответ: если пряма перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Слайд 34. Как определяется расстояние от точки до прямой на плоскости?
Ответ:
как длина перпендикуляра, проведённого из точки к данной прямой.
5. По
рисунку назовите:
перпендикуляр, основание
перпендикуляра, наклонную к
плоскости α, основание
наклонной и её проекцию на
плоскость α.
6. Сформулируйте теорему о трёх перпендикулярах.
α
K
D
P
Слайд 4Теорема о трёх перпендикулярах.
Прямая, проведённая в плоскости через основание
наклонной
перпендикулярно к её проекции на эту
плоскость, перпендикулярна и к самой
наклонной
Обратно: прямая, проведённая в плоскости через
основание наклонной перпендикулярно к ней
перпендикулярна и к её проекции.
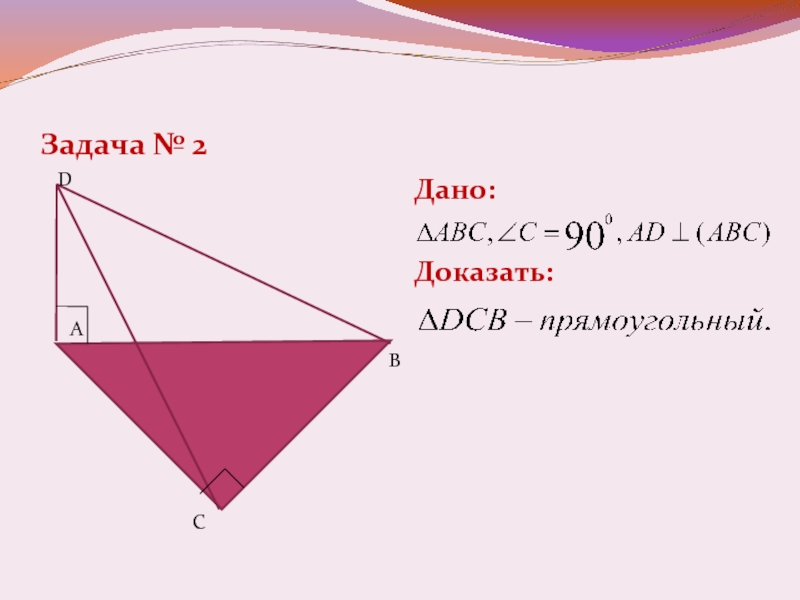
Слайд 5Задача № 1
Дано:
АВСК –прямоугольник.
Доказать:
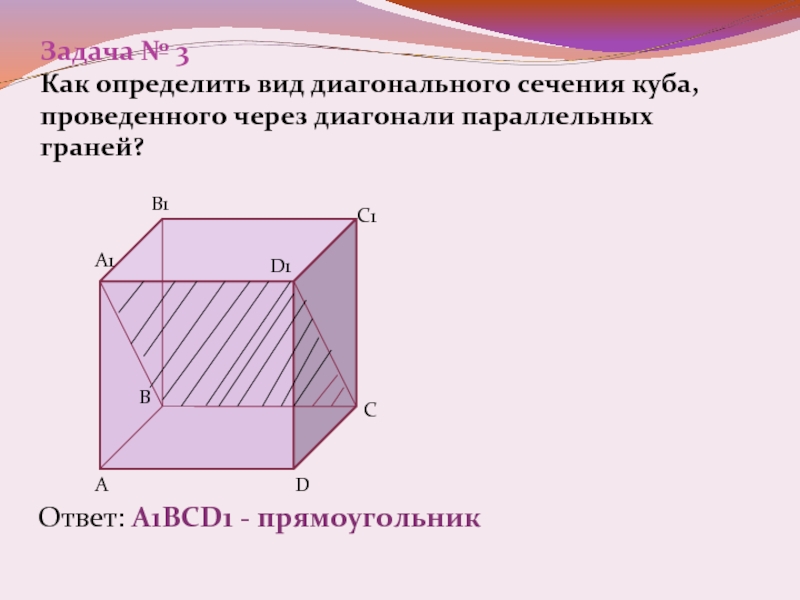
Слайд 7Задача № 3
Как определить вид диагонального сечения куба, проведенного через
диагонали параллельных граней?
Ответ: А1ВСD1 - прямоугольник
Слайд 8Задача №4
На изображении куба построить несколько прямых перпендикулярных диагонали
куба.
Слайд 9Задача №154 (Атанасян)
Прямая BD перпендикулярна к плоскости треугольника
АВС. Известно, что BD = 9 см,
АС
= 10 см, ВС = ВА = 13 см.
Найдите: а) расстояние от точки D до прямой АС; б) площадь треугольника ACD.
Слайд 10Задача № 158
Через вершину В ромба ABCD проведена прямая ВМ,
перпендикулярная к его плоскости. Найдите расстояние от точки М до
прямы, содержащих стороны ромба, если АВ = 25 см, угол BAD равен 60 градусам, ВМ = 12,5 см.
Слайд 11Задача №161
Луч ВА не лежит в плоскости неразвернутого угла CBD.
Докажите, что если угол АВС равен углу ABD, причем угол
АВС меньше 90 градусов, то проекцией луча ВА на плоскость CBD является биссектриса угла CBD.
Слайд 12Верно ли, что две прямые, параллельные одной плоскости, перпендикулярны (две
прямые, перпендикулярные к одной плоскости, параллельны).
Может ли прямая, перпендикулярная к
плоскости, скрещиваться с прямой, лежащей в этой плоскости (прямая, перпендикулярная к плоскости, быть параллельна прямой, лежащей в этой плоскости)?
Верно ли, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым этой плоскости (она перпендикулярна к двум прямым, параллельным этой плоскости)?
Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости (две пересекающиеся прямые быть перпендикулярными к одной плоскости)?
Слайд 13Верно ли, что любая из трех взаимно перпендикулярных прямых перпендикулярна
к плоскости двух других прямых (две прямые в пространстве, перпендикулярные
к третьей прямой, параллельны)?
Могут ли пересекаться две плоскости, перпендикулярные к одной прямой ( прямая а и плоскость, перпендикулярные к одной прямой с)?
Верно ли, что длина перпендикуляра меньше длины наклонной, проведенной из той же точки (длина перпендикуляра меньше длины проекции наклонной, проведенной из той же точки)?
Слайд 14Критерии оценок
7 правильных ответов – «5»
6 правильных ответов – «4»
5
правильных ответов – «3»
Слайд 15I уровень.(на «3»)
Дано:, АС ┴ ВС, SA = SB =
SC =10 см; СМ =5 см –медиана.
Найти: SM (расстояние от
точки S до плоскости (АВС)).
II уровень ( на «4»)
Дано: ABCD – прямоугольник; АК ┴ (АВС), KD= 6 см, КВ = = 7 см, КС = 9 см.
Найти: расстояние от точки К до (АВС).
III уровень.( на «5»)
Дано: АВ = 17 см, АС = 15 см, ВС = 8 см, АМ ┴ (АВС),
<А – меньший,
АМ = 20 см.
Найти: МЕ.
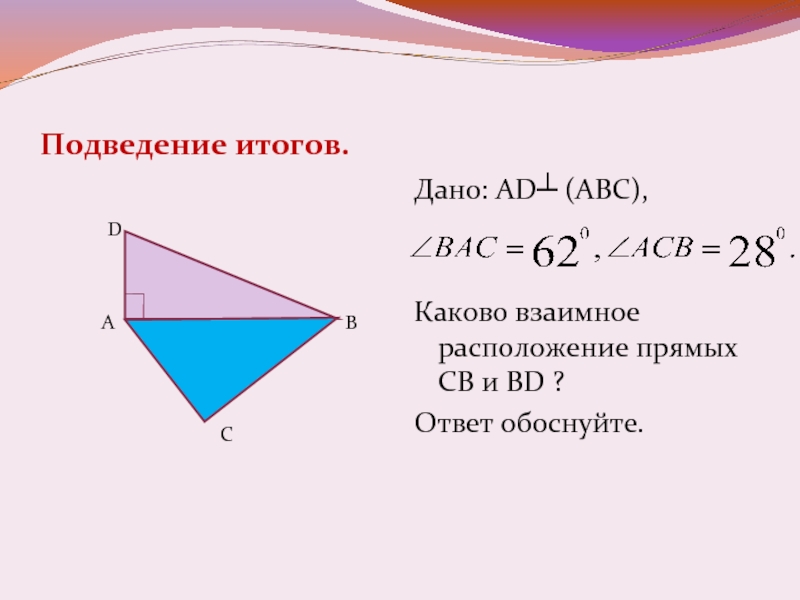
Слайд 16Подведение итогов.
Дано: AD┴ (АВС),
Каково взаимное расположение прямых СВ и BD
?
Ответ обоснуйте.
D
A
B
C