Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о трех перпендикулярах, ее применение при решении задач
Содержание
- 1. Теорема о трех перпендикулярах, ее применение при решении задач
- 2. ОБУЧАЮЩАЯ :обосновать необходимость теоремы о трех перпендикулярахсформировать
- 3. Проверка домашнего задания.ПЛАН УРОКАI. Организационный момент.III. Актуализация
- 4. «НАЧИНАТЬ ИССЛЕДОВАНИЯ МОЖНО ПО-РАЗНОМУ... Все равно начало
- 5. Акцентируем теорию по теме. 1. Угол между прямыми равен
- 6. 4. Как определяется расстояние от точки до
- 7. Теорема о трёх перпендикулярах.Прямая, проведённая в плоскости
- 8. Дано: α , АС – наклонная, ВС
- 9. Iспособ (от противного)Теорема: Если прямая, проведенная на
- 10. II способ (свойства равнобедренного треугольника)
- 11. III способ (теорема Пифагора)Доказательство: На
- 12. IV способ (векторный)Доказательство:Зададим векторы Умножим обе части
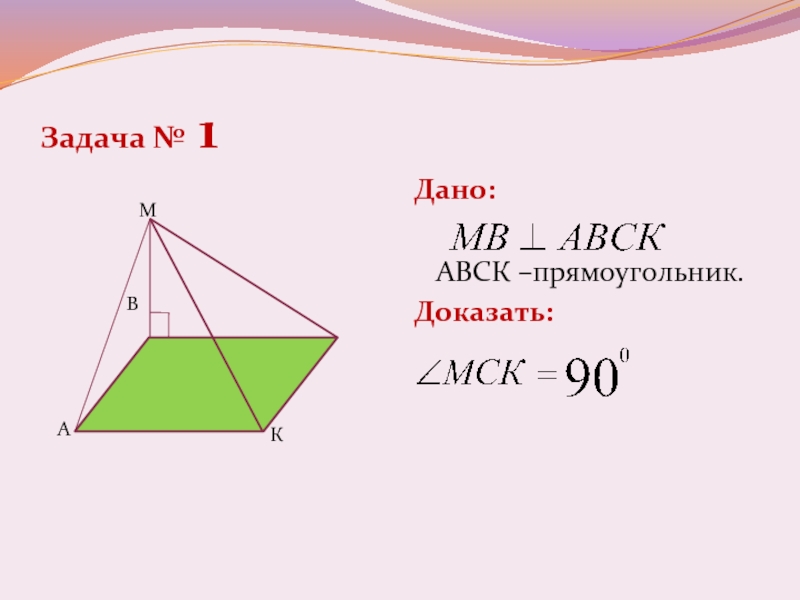
- 13. Задача № 1Дано: АВСК –прямоугольник.Доказать:
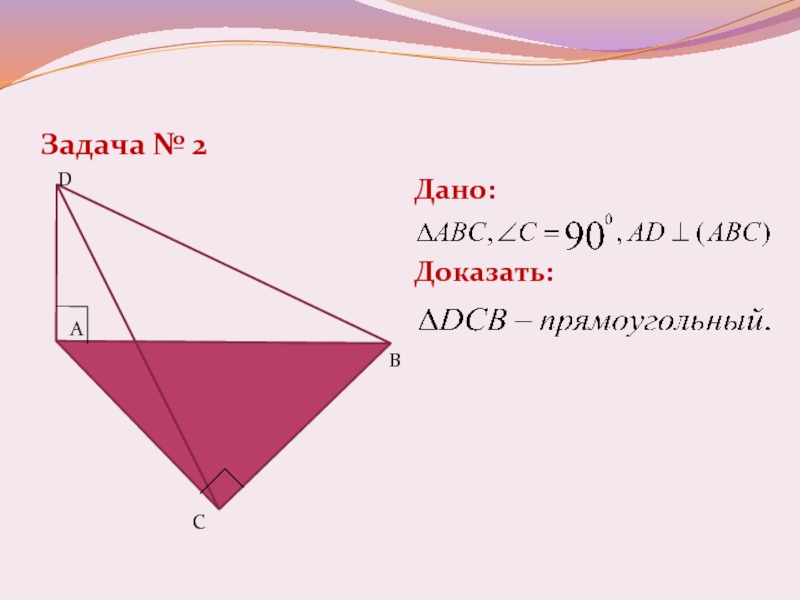
- 14. Задача № 2Дано:Доказать:C
- 15. Задача № 3 Как определить вид диагонального
- 16. Задача №4 На изображении куба построить несколько прямых перпендикулярных диагонали куба.
- 17. Задача №154 (Атанасян) Прямая BD перпендикулярна
- 18. Задача № 158Через вершину В ромба ABCD
- 19. Задача №161Луч ВА не лежит в плоскости
- 20. Верно ли, что две прямые, параллельные одной
- 21. Верно ли, что любая из трех взаимно
- 22. Критерии оценок 7 правильных ответов – «5»
- 23. I уровень.(на «3»)Дано:, АС ┴ ВС, SA
- 24. Подведение итогов.Дано: AD┴ (АВС),Каково взаимное расположение прямых СВ и BD ?Ответ обоснуйте.DABC
- 25. ДОМАШНЕЕ ЗАДАНИЕ1. № 145, 143, 140.2. Ответить
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 «Теорема о трех перпендикулярах, ее применение при решении задач» учитель математики
муниципального общеобразовательного учреждения
Арсугская СОШ
Алавдинов Рамазан Гасанович
Слайд 2ОБУЧАЮЩАЯ :
обосновать необходимость теоремы о трех перпендикулярах
сформировать видение изученной закономерности
в различных ситуациях: при решении задач на доказательство или задач,
требующих найти численное (или буквенное значение) какого-либо элемента .учиться умению читать чертеж,
учить умению объяснять, комментировать выполняемое упражнение в виде цельного связного рассказа.
ВОСПИТАТЕЛЬНАЯ :
способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания,
развитие навыков исследовательской деятельности (планирование, выдвижение гипотез, анализ, обобщение).
РАЗВИВАЮЩАЯ :
развивать у учащихся коммуникативные компетенции,
способствовать развитию творческой деятельности учащихся, потребности к самообразованию.
ЦЕЛЬ УРОКА
Слайд 3Проверка домашнего задания.
ПЛАН УРОКА
I. Организационный момент.
III. Актуализация знаний.
IY. Применение теории
на практике.
Y. Осмысление содержания и последовательности применения практических действий при
выполнении предстоящих заданийYI. Самостоятельное выполнение учащимися заданий под контролем учителя
YII. Подведение итогов.
YIII. Домашнее задание.
Дерзай !!!
II.
Слайд 4«НАЧИНАТЬ ИССЛЕДОВАНИЯ МОЖНО ПО-РАЗНОМУ... Все равно начало почти всегда оказывается
весьма несовершенной, нередко безуспешной попыткой. ЕСТЬ ИСТИНЫ, как страны, НАИБОЛЕЕ
УДОБНЫЙ ПУТЬ К КОТОРЫМ СТАНОВИТСЯ ИЗВЕСТНЫМ ЛИШЬ ПОСЛЕ ТОГО, КАК МЫ ИСПРОБУЕМ ВСЕ ПУТИ. Кому-то приходится, рискуя собой, сходить с проторенной дороги, чтобы указать другим правильный путь... НА ПУТИ К ИСТИНЕ МЫ ПОЧТИ ВСЕГДА ОБРЕЧЕНЫ СОВЕРШАТЬ ОШИБКИ» (Дени Дидро).ЭПИГРАФ К УРОКУ
Denis Diderot
1713 - 1784
Екатерина II
Слайд 5Акцентируем теорию по теме.
1. Угол между прямыми равен 90˚. Как называются
такие прямые?
Ответ: перпендикулярные.
2. Верно ли утверждение: «прямая называется перпендикулярной плоскости, если
она перпендикулярна некоторой прямой, лежащей этой плоскости»Ответ: да.
3. Сформулируйте признак перпендикулярности прямой и плоскости.
Ответ: если пряма перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Слайд 64. Как определяется расстояние от точки до прямой на плоскости?
Ответ:
как длина перпендикуляра, проведённого из точки к данной прямой.
5. По
рисунку назовите:перпендикуляр, основание
перпендикуляра, наклонную к
плоскости α, основание
наклонной и её проекцию на
плоскость α.
6. Сформулируйте теорему о трёх перпендикулярах.
α
K
D
P
Слайд 7Теорема о трёх перпендикулярах.
Прямая, проведённая в плоскости через основание
наклонной
перпендикулярно к её проекции на эту
плоскость, перпендикулярна и к самой
наклоннойОбратно: прямая, проведённая в плоскости через
основание наклонной перпендикулярно к ней
перпендикулярна и к её проекции.
Слайд 8Дано: α , АС – наклонная,
ВС – проекция, ВС
┴ с , АВ ┴ α.
Доказать: АС ┴ с.
Доказательство.
1.Проведем СА1
┴ с . 2.СА1||АВ по теореме.(Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны).
3.Проведем через АВ и СА1 плоскость β.
4.с ┴ СА, с ┴ ВС (по Теореме: «Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости».),с ┴ β, значит,
с ┴АС.
Слайд 9Iспособ (от противного)
Теорема: Если прямая, проведенная на плоскости через основание
наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
Доказательство:
Пусть t ┴ ОА. Допустим, что SA не перпендикулярна прямой t. Проведем SB ┴ t, тогда SA> SB. Из прямоугольных треугольников SOA и SOB:Получаем: ОА>OB. Между тем ОА < OB, так как ОА ┴ t по условию. К данному противоречию нас привело предположение, что SA не перпендикулярна прямой t. Значит, SA┴ t.
S
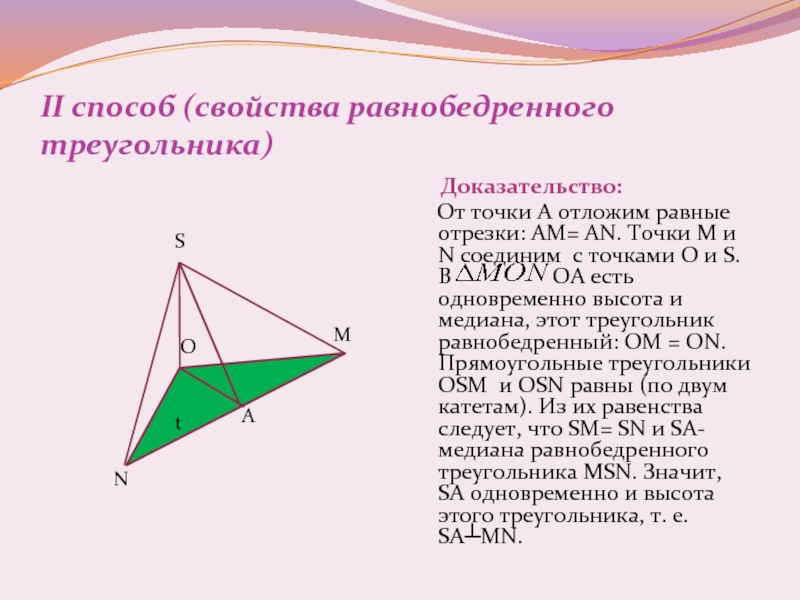
Слайд 10II способ (свойства равнобедренного треугольника)
Доказательство:
От
точки А отложим равные отрезки: АМ= АN. Точки М и
N соединим с точками O и S. В ОА есть одновременно высота и медиана, этот треугольник равнобедренный: ОМ = ОN. Прямоугольные треугольники OSM и OSN равны (по двум катетам). Из их равенства следует, что SM= SN и SA- медиана равнобедренного треугольника MSN. Значит, SA одновременно и высота этого треугольника, т. е. SA┴MN.Слайд 11III способ (теорема Пифагора)
Доказательство:
На прямой t возьмем
произвольную точку В и соединим ее с точками О и
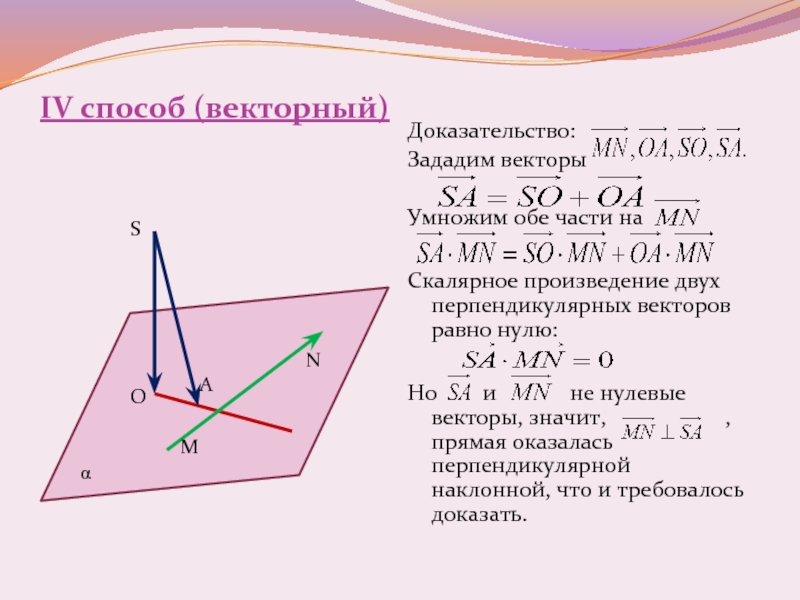
S. Из прямоугольных треугольников SOB, SOA и AOB: = SO2+ OB2, SA2 = =SO2+ OA2, OB2- OA2= AB2. Вычтя из первого равенства второе, получим:SB2 – SA2 = =OB2 – OA2. Приняв во внимание третье равенство, будем иметь: SB2 – SA2 = AB2, SB2 = SA2 +AB2. Согласно теореме, обратной теореме Пифагора, SA┴AB, т. е. t┴SA.Слайд 12IV способ (векторный)
Доказательство:
Зададим векторы
Умножим обе части на
Скалярное произведение двух
перпендикулярных векторов равно нулю:
Но и
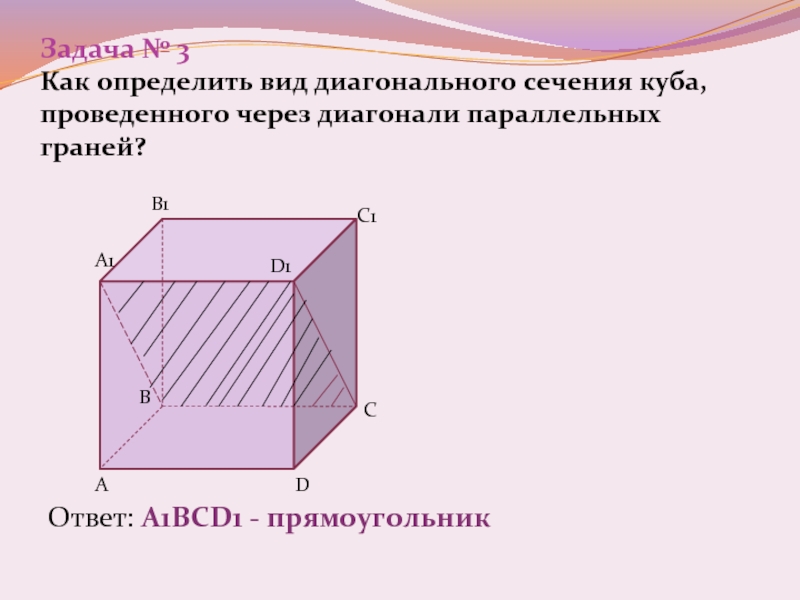
не нулевые векторы, значит, , прямая оказалась перпендикулярной наклонной, что и требовалось доказать.Слайд 15Задача № 3 Как определить вид диагонального сечения куба, проведенного через
диагонали параллельных граней?
Ответ: А1ВСD1 - прямоугольник
Слайд 17Задача №154 (Атанасян)
Прямая BD перпендикулярна к плоскости треугольника
АВС. Известно, что BD = 9 см,
АС
= 10 см, ВС = ВА = 13 см.Найдите: а) расстояние от точки D до прямой АС; б) площадь треугольника ACD.
Думай
Д
У
М
А
Й
!
!
!
Слайд 18Задача № 158
Через вершину В ромба ABCD проведена прямая ВМ,
перпендикулярная к его плоскости. Найдите расстояние от точки М до
прямы, содержащих стороны ромба, если АВ = 25 см, угол BAD равен 60 градусам, ВМ = 12,5 см.Р
Е
Ш
А
Й
!!!
Слайд 19Задача №161
Луч ВА не лежит в плоскости неразвернутого угла CBD.
Докажите, что если угол АВС равен углу ABD, причем угол
АВС меньше 90 градусов, то проекцией луча ВА на плоскость CBD является биссектриса угла CBD.о
трех
перпендикуляра х -
это
. . .
Теорема
Слайд 20Верно ли, что две прямые, параллельные одной плоскости, перпендикулярны (две
прямые, перпендикулярные к одной плоскости, параллельны).
Может ли прямая, перпендикулярная к
плоскости, скрещиваться с прямой, лежащей в этой плоскости (прямая, перпендикулярная к плоскости, быть параллельна прямой, лежащей в этой плоскости)?Верно ли, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым этой плоскости (она перпендикулярна к двум прямым, параллельным этой плоскости)?
Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости (две пересекающиеся прямые быть перпендикулярными к одной плоскости)?
Слайд 21Верно ли, что любая из трех взаимно перпендикулярных прямых перпендикулярна
к плоскости двух других прямых (две прямые в пространстве, перпендикулярные
к третьей прямой, параллельны)?Могут ли пересекаться две плоскости, перпендикулярные к одной прямой ( прямая а и плоскость, перпендикулярные к одной прямой с)?
Верно ли, что длина перпендикуляра меньше длины наклонной, проведенной из той же точки (длина перпендикуляра меньше длины проекции наклонной, проведенной из той же точки)?
Слайд 22Критерии оценок 7 правильных ответов – «5» 6 правильных ответов – «4» 5
правильных ответов – «3»
Слайд 23I уровень.(на «3»)
Дано:, АС ┴ ВС, SA = SB =
SC =10 см; СМ =5 см –медиана.
Найти: SM (расстояние от
точки S до плоскости (АВС)).II уровень ( на «4»)
Дано: ABCD – прямоугольник; АК ┴ (АВС), KD= 6 см, КВ = = 7 см, КС = 9 см.
Найти: расстояние от точки К до (АВС).
III уровень.( на «5»)
Дано: АВ = 17 см, АС = 15 см, ВС = 8 см, АМ ┴ (АВС),
<А – меньший,
АМ = 20 см.
Найти: МЕ.
Слайд 24Подведение итогов.
Дано: AD┴ (АВС),
Каково взаимное расположение прямых СВ и BD
?
Ответ обоснуйте.
D
A
B
C
Слайд 25ДОМАШНЕЕ ЗАДАНИЕ
1. № 145, 143, 140.
2. Ответить на вопросы пп
19, 20.
3. Дополнительная задача: Через сторону AD ромба ABCD проведена
плоскость α. Найдите расстояние от прямой ВС до плоскости α, если площадь ромба равна 80 ,высота – 8 см, а угол между проекцией стороны CD и прямой AD равен 45 градусов.Дальнейших
успехов !!!
СПАСИБО!