Теорема отсчетов Котельникова

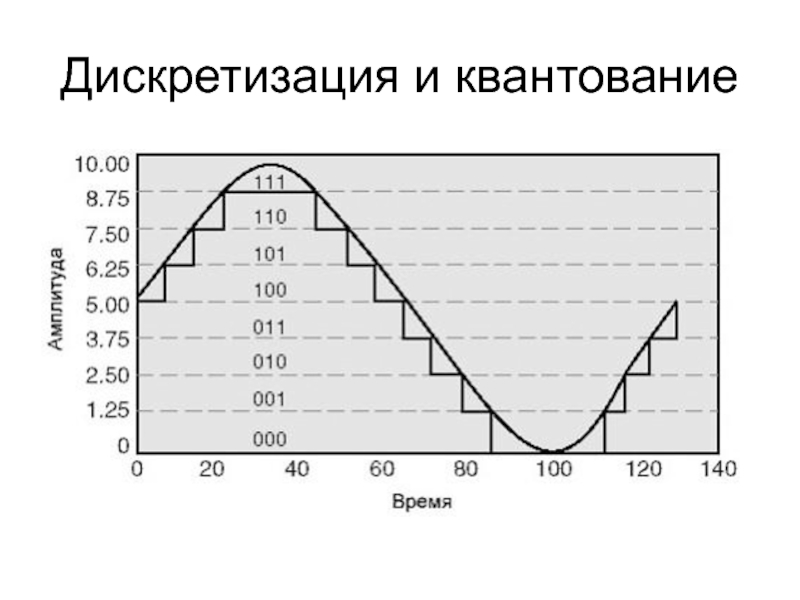
ввода аналоговых сигналов от объектов в компьютер. При этом должно

осуществляться аналого-цифровое преобразование измерительной информации, которое производится аналого-цифровым преобразователем – АЦП.
Входной величиной АЦП обычно является напряжение, выходной величиной – цифровой код.
При преобразовании напряжения в цифровой код выполняются три независимые операции: дискретизация, квантование и кодирование.

напряжения v(t) в последовательность мгновенных значений v(ti), отнесенных к некоторым

фиксированным моментам времени ti.
В основе дискретизации сигналов лежит принципиальная возможность их представления в виде взвешенных сумм:


где аi — некоторые коэффициенты или отсчеты, характеризующие исходный сигнал в дискретные моменты времени, φι - набор элементарных функций, используемых при восстановлении сигнала по его отсчетам.

теорема отсчетов (в отечественной литературе – теорема Котельникова), согласно которой

в качестве коэффициентов ai нужно использовать мгновенные значения сигнала v(ti) в дискретные моменты времени . Период дискретизации при этом следует выбирать из условия



- где fm – верхняя граница спектра исходного сигнала.

ограниченной верхней частотой спектра fm может быть представлена отчетами iT,

взятыми с периодом дискретизации




- где - функция отсчетов

- (базис Котельникова), то есть для восстановления непрерывного сигнала по его выборкам достаточно располагать функцией sinc(t)=sin(t)/t с учетом ее особого значения sinc(t)=1 при t=0.

и иметь на протяжении периода конечное число экстремальных значений.

при котором возможно восстановление формы сигнала, то есть должно выполняться

условие




Таким образом, чтобы восстановить исходный сигнал по его отсчетам, надо иметь их численные значения и знать значение периода дискретизации T. Все эти данные нетрудно хранить в запоминающем устройстве. Если увеличить T при восстановлении сигнала в k раз, то восстановленный сигнал без изменения формы будет растянут в k раз. И наоборот.

функции v(ti) ограничиваются только определенными уровнями, которые называются уровнями квантования.

В отличие от дискретизации, которая теоретически является обратимой операцией, квантование представляет собой необратимое преобразование исходной последовательности и сопровождается появлением неизбежных погрешностей. При равномерном квантовании расстояние между двумя соседними значениями делается постоянным. Разность между двумя соседними значениями квантованной величины называется шагом квантования q.

По существу квантование представляет собой операцию округления непрерывной величины до ближайшего целого значения. В АЦП погрешность квантования определяется как единица младшего значащего разряда (МЗР).

не зависит от того, в какой части диапазона находится х.

Абсолютная погрешность квантования, приведенная ко входу, составит величину


а к выходу

цифрового кода, т. е. последовательности цифр, подчиненных определенному закону. С

помощью операции кодирования осуществляется условное представление численного значения величины. Выходной величиной АЦП обычно является цифровой двоичный код. При работе с однополярным входным сигналом ис­пользуется прямой код, а при двуполярном сигнале - дополнительный.