TheSlide.ru

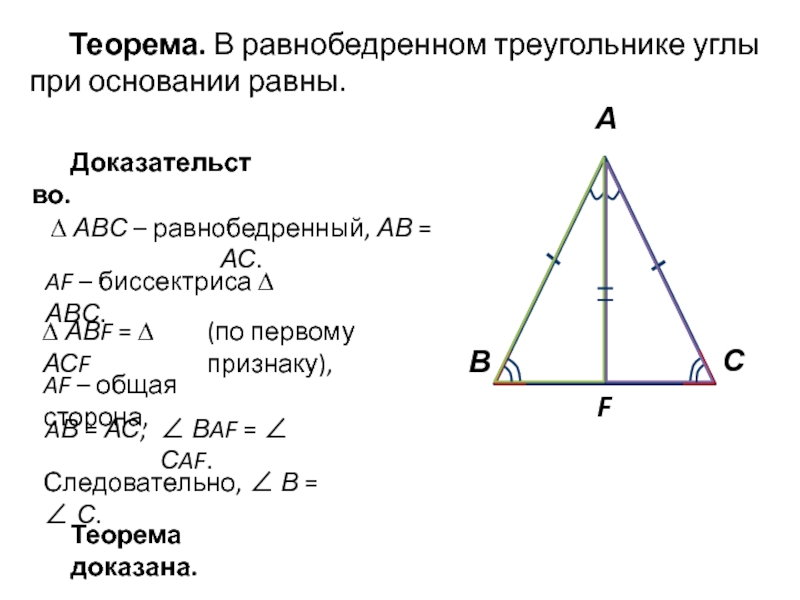
Теорема. В равнобедренном треугольнике углы при основании

Содержание

1. Теорема. В равнобедренном треугольнике углы при основании
2. Теорема. В равнобедренном треугольнике биссектриса, проведённая к
3. Третий признак равенства треугольниковЕсли три стороны одного
4. Доказательство. А1В1С1Пусть АВ = А1В1,ВС = В1С1,СА
5. 2)АС = А1С1,∆ СА1С1 – равнобедренный.∠ С
6. 3)СА1 (А)В1 (В)С1∆ СА1С1, ∆ СВ1С1 –
7. Скачать презентанцию

Теорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. Доказательство.AВ = АС, ∠ ВAF = ∠ СAF. AF – медиана ∆ АВС.∠ AFВ = ∠ АFС, AF –

Главная
Разное
Теорема. В равнобедренном треугольнике углы при основании

Слайды и текст этой презентации

Слайд 1Теорема. В равнобедренном треугольнике углы при основании равны.
Доказательство.
AВ =

АС,
∠ ВAF = ∠ СAF.
Теорема доказана.
(по первому признаку),

Теорема. В равнобедренном треугольнике углы при основании равны. Доказательство.AВ = АС, ∠ ВAF = ∠ СAF. Теорема

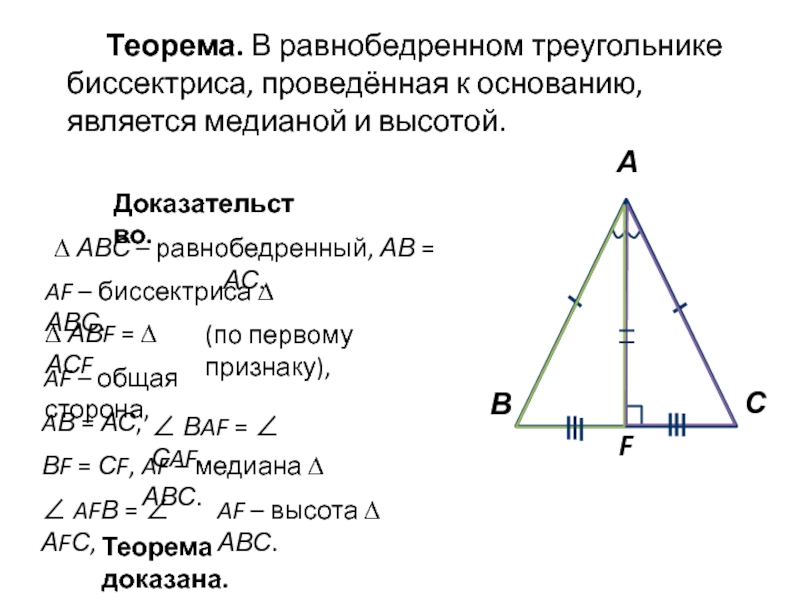
Слайд 2Теорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой

и высотой.
Доказательство.
AВ = АС,
∠ ВAF = ∠ СAF.

AF – медиана ∆ АВС.

∠ AFВ = ∠ АFС,

AF – высота ∆ АВС.

Теорема доказана.

(по первому признаку),

Теорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. Доказательство.AВ = АС, ∠ ВAF

Слайд 3Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны

трём сторонам другого треугольника, то такие треугольники равны.
А
А1
С1
В1
С
В

Третий признак равенства треугольниковЕсли три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники

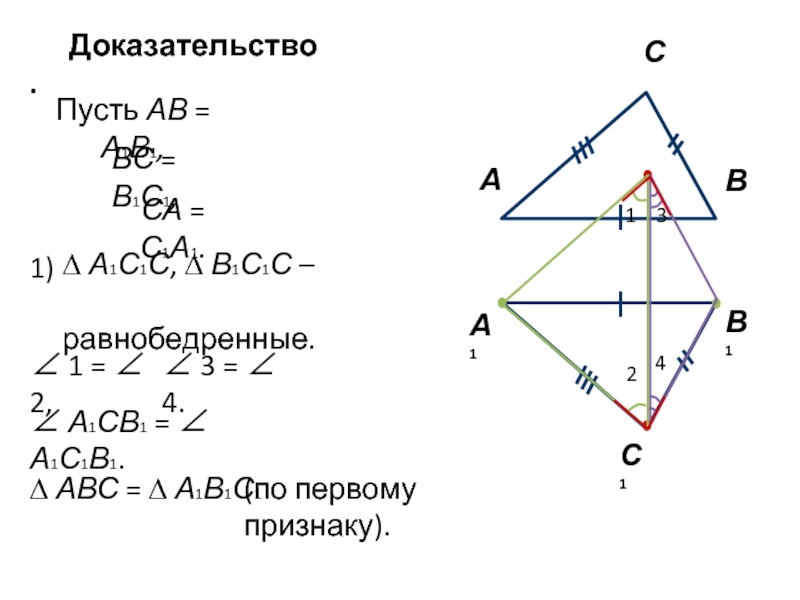
Слайд 4Доказательство.
А1
В1
С1
Пусть АВ = А1В1,
ВС = В1С1,
СА = С1А1.
1)
∆ А1С1С,

∆ В1С1С –

равнобедренные.

∠ 1 = ∠ 2,

∠ 3 = ∠ 4.

∠ А1СВ1 = ∠ А1С1В1.

∆ АВС = ∆ А1В1С1

(по первому признаку).

1

2

3

4

Доказательство. А1В1С1Пусть АВ = А1В1,ВС = В1С1,СА = С1А1.1)∆ А1С1С, ∆ В1С1С –

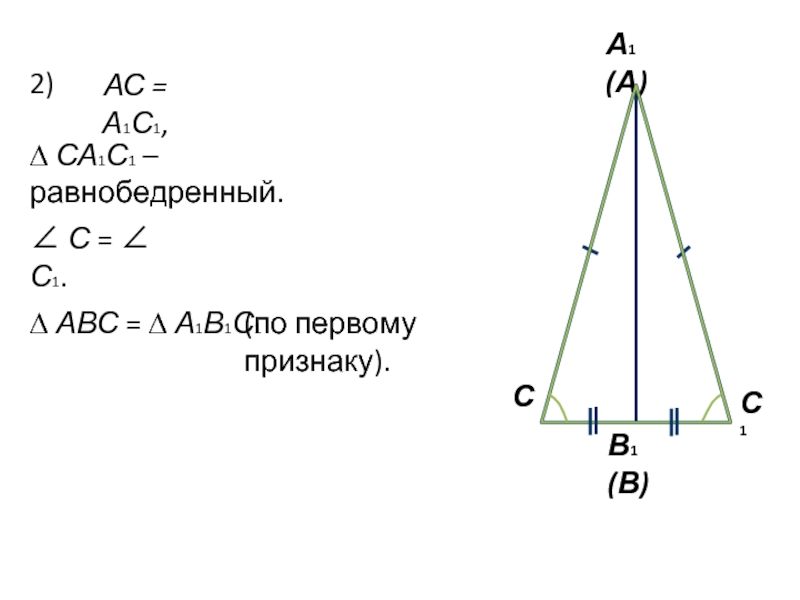
Слайд 52)
АС = А1С1,
∆ СА1С1 – равнобедренный.
∠ С = ∠ С1.
∆

АВС = ∆ А1В1С1
(по первому признаку).
С
А1 (А)
В1 (В)
С1

2)АС = А1С1,∆ СА1С1 – равнобедренный.∠ С = ∠ С1.∆ АВС = ∆ А1В1С1(по первому признаку).СА1 (А)В1

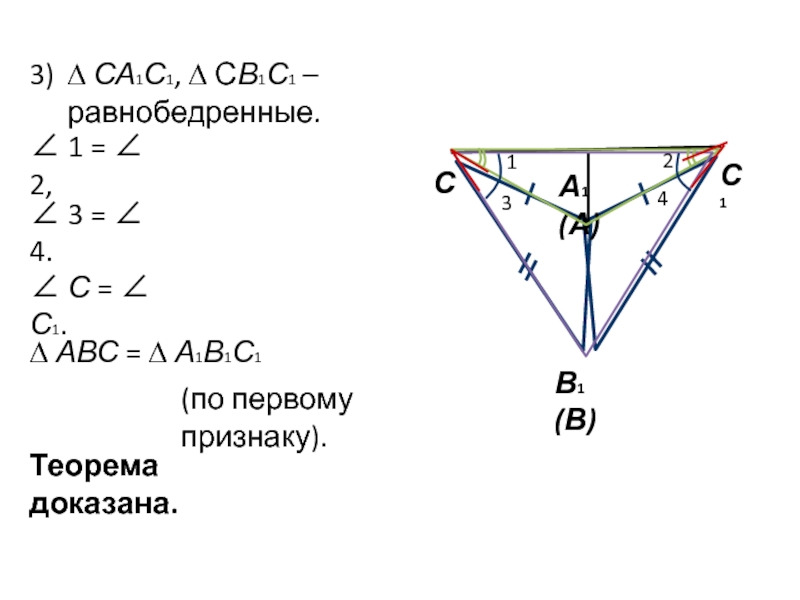
Слайд 63)
С
А1 (А)
В1 (В)
С1
∆ СА1С1, ∆ СВ1С1 – равнобедренные.
∠ 3 =

∠ 4.
∠ С = ∠ С1.
∆ АВС = ∆ А1В1С1
(по

первому признаку).

Теорема доказана.

3

4

3)СА1 (А)В1 (В)С1∆ СА1С1, ∆ СВ1С1 – равнобедренные.∠ 3 = ∠ 4.∠ С = ∠ С1.∆ АВС

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей