Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоретические языки запросов в реляционных БД
Содержание
- 1. Теоретические языки запросов в реляционных БД
- 2. Введение В реляционных СУБД для выполнения
- 3. Языки реляционной алгебры являются процедурными. Опе-раторы этой
- 4. Языки исчислений, в отличие от реляционной
- 5. Реляционные таблицы для примеров
- 6. Таблица S
- 7. Таблица P
- 8. Слева таблица SP Первичными ключами этих
- 9. 1. Реляционная алгебра Вариант реляционной алгебры,
- 10. Перечисленный набор из 8 операций является избыточным.
- 11. С другой стороны указанных 8 опера-ций недостаточно
- 12. Операции реляционной алгебры могут выполняться над одним
- 13. 1.1. Объединение Объединением двух совместимых отношений
- 14. Пример 1 Пусть отношением R1 будет
- 15. 1.2. Вычитание Разность двух совместимых отношений
- 16. 1.3. Пересечение Пересечением двух совместимых отношений
- 17. 1.4. Декартово произведение Декартовым произведением отношения
- 18. Замечание 1 В реляционной алгебре используется
- 19. Пример 2 Пусть отношение R1 представляет
- 20. Замечание 2 Напрямую операция декартова произ-ведения
- 21. 1.5. Выборка (ограничение) Выборка отношения R
- 22. Пример 3Запрос P WHERE Вес
- 23. Пример 4 Для операции выборки используют
- 24. Проекция отношения A на различные
- 25. Дополнительные варианты записи операции проекцииОтсутствие списка атрибутов
- 26. Замечание 3 Если операцию выборки можно
- 27. 1.7. Деление Операция деления определена для
- 28. Результатом деления отношения R1на отношение R2 является
- 29. Пример 5 Пусть R1 - проекция
- 30. Результатом деления отношения R1 на отношение R2
- 31. 1.8. Соединение Операция соединения используется для
- 32. У операции соединения есть несколько вариантов: естественное
- 33. 1.8. 1. Естественное соединение Естественное соединение
- 34. Берется декартово произведение отношений R1 и
- 35. 1.8. 2. Тета-соединение и эквисоединение Тета-соединение
- 36. Замечание 4 Тета-соединение, в отличие от
- 37. 1.8. 3. Внешнее соединение Внешнее соединение
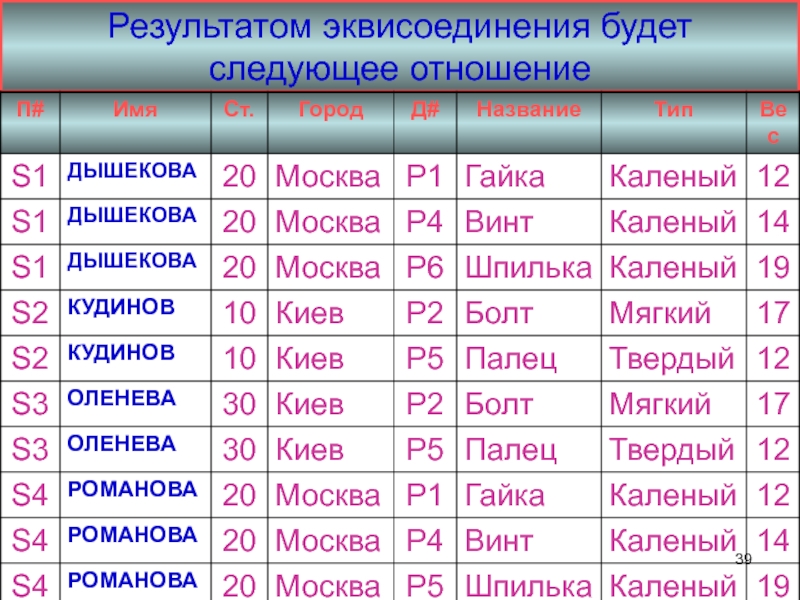
- 38. Пример 6 (эквисоединение) Найдем соединение отношений
- 39. Результатом эквисоединения будет следующее отношение
- 40. Обзор дополнительных операций реляционной алгебры, предложенных Дейтом2Д.
- 41. В операции расширения имя нового атрибута не
- 42. 3Д. Операция подведения итогов Синтаксис этой
- 43. Результатом операции подведения итогов является отношение R
- 44. Пример 6 Пусть требуется вы-числить число
- 45. 4Д. Операция присваивания Синтаксис операции::= ,
- 46. 5Д. Операция вставки Синтаксис операции:INSERT INTO
- 47. 6Д. Операция обновления Синтаксис операции:UPDATE ,
- 48. 7Д. Операция удаления 8Д. Операции реляционного сравненияСинтаксис
- 49. Замечание 5 При записи выражений в
- 50. выражения можно заменять другими выражениями, получающи-
- 51. 2. Реляционное исчисление Принципиальное отличие
- 52. Понятие реляционного исчисления, как языка работы с
- 53. 2.1. Исчисление кортежей В исчислении кортежей,
- 54. - идентификатор пере- менной кортежа (области
- 55. Все элементы списка должны быть сов-местимы по
- 56. Пример 1 Варианты описаний:RANGE OF SX
- 57. Переменные SX и SPX в первых двух
- 58. Пример 2 Записать выражение на языке
- 59. Замечание В исчисление кортежей можно добавить
- 60. 2.2. Исчисление доменов Исчисление доменов было
- 61. Отличительной особенностью исчи-сления доменов от исчисления кортежей
- 62. Проверяемое условие будет истинным тогда и только
- 63. Примеры выражений исчисления доменов(SX) WHERE S (П#:SX)
- 64. Третье выражение соответствует запросу на получение имен
- 65. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Теоретические языки запросов в реляционных базах данных
1. Реляционная алгебра
2. Реляционное исчисление
Слайд 2Введение
В реляционных СУБД для выполнения операций над отношениями
исполь-зуется две группы языков, имеющие в качестве своей математической основы
теоретические языки запросов, предло-женные Э. Коддом:реляционная алгебра;
реляционное исчисление.
Слайд 3Языки реляционной алгебры являются процедурными. Опе-раторы этой алгебры состоят из
операндов, в роли которых выступают отношения, и реля-ционных операций. Резуль-татом
реляционной операции является отношение.Слайд 4 Языки исчислений, в отличие от реляционной алгебры, являются непроцедурными
(описательными или декларативными) и позволяют выражать запросы с помощью предикатов
первого порядка. Запрос к БД, выполненный с использованием подобного языка, содержит лишь информацию о желаемом результате, а не как его получить.Слайд 5Реляционные таблицы для примеров
В дальнейшем при
рассмотрении язы-ков реляционной алгебры и реляцион-ного исчисления для демонстрацион-ных примеров
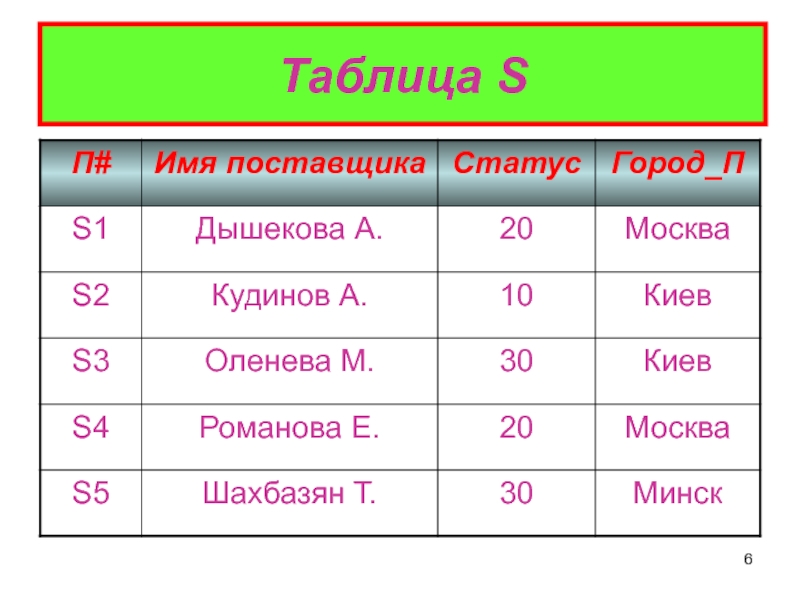
будем использовать БД, включающую в себя следующие три таблицы:Таблица S (поставщики деталей).
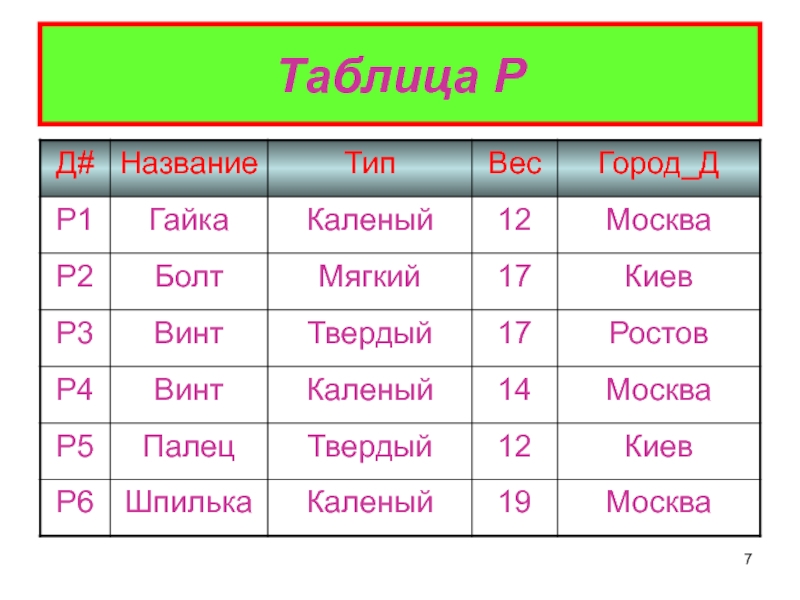
Таблица P (характеристики деталей).
Таблица SP (поставки).
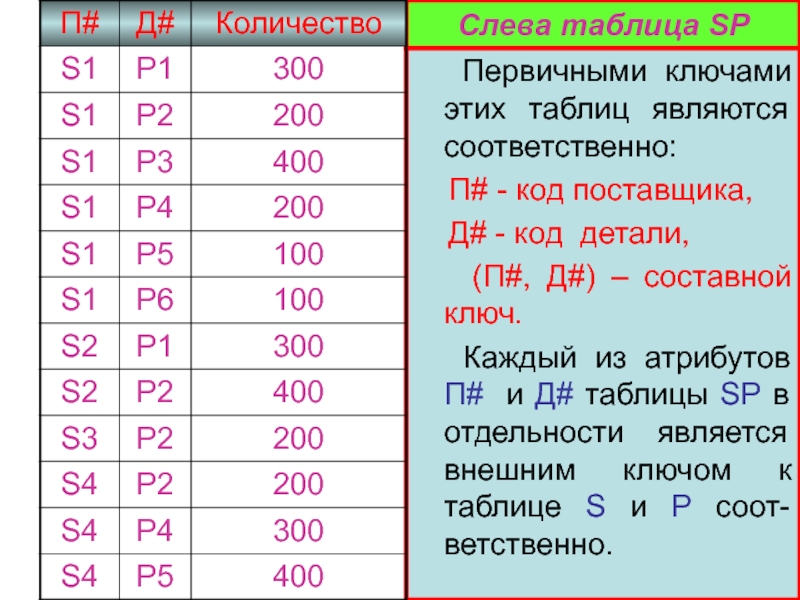
Слайд 8Слева таблица SP
Первичными ключами этих таблиц являются соответственно:
П# - код поставщика,
Д# - код детали,
(П#, Д#) – составной ключ.Каждый из атрибутов П# и Д# таблицы SP в отдельности является внешним ключом к таблице S и P соот-ветственно.
Слайд 91. Реляционная алгебра
Вариант реляционной алгебры, предло-женный Э. Коддом,
можно разделить на две группы: 1) базовые теоретико-мно-жественные операции –
объединение, пересечение, разность и декартово произведение; 2) специальные опера-ции - проекция, селекция, деление и соединение.Слайд 10Перечисленный набор из 8 операций является избыточным. Минимально необходимый набор
составляет 5 операций – объединение, вычитание, декартово произведение, проекция и
выборка. Три оставшиеся операции можно определить через указанные выше 5 операций, например, сое-динение – это проекция выборки де-картова произведения.Слайд 11С другой стороны указанных 8 опера-ций недостаточно для построения ре-альной
СУБД на принципах реляцион-ной алгебры. Требуются расширения, включающие операции переименования
атрибутов, образования новых вычис-ляемых атрибутов, вычисления ито-говых функций и др. Эти допол-нительные операции были введены К. ДЖ. Дейтом.Слайд 12Операции реляционной алгебры могут выполняться над одним отношением – унарные
операции, - например, проекция; над двумя отношениями – бинарные операции,
например, объединение.При выполнении бинарных операций участвующие в операциях отношения должны быть совместимы по структуре, что означает совместимость имен атрибутов и типов соответствующих доменов. Частным случаем совместимости является идентичность (совпадение).
Слайд 131.1. Объединение
Объединением двух совместимых отношений R1 и R2
с одинаковы-ми заголовками называется отно-шение R, содержащее все элемен-ты исходных
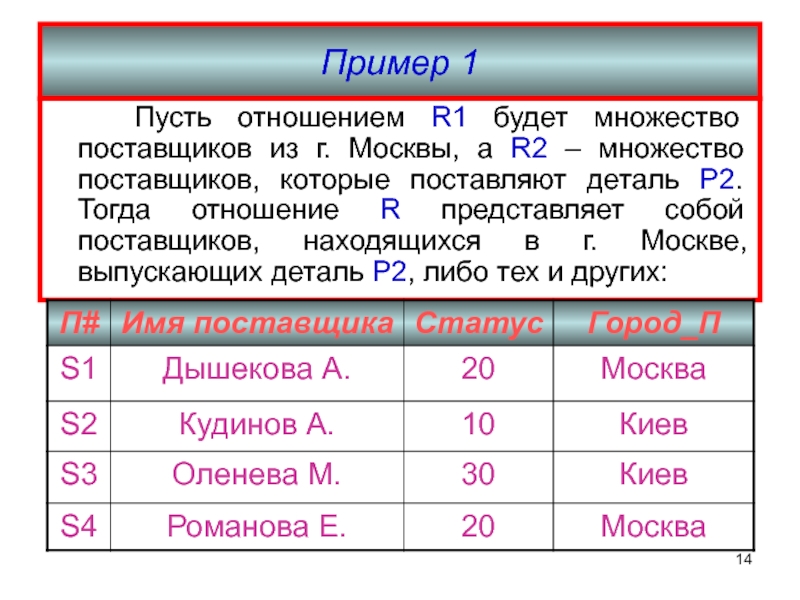
отношений (с исклю- чением повторений кортежей). Обозначение: R= R1 UNION R2Слайд 14Пример 1
Пусть отношением R1 будет множество поставщиков из
г. Москвы, а R2 – множество поставщиков, которые поставляют деталь
P2. Тогда отношение R представляет собой поставщиков, находящихся в г. Москве, выпускающих деталь P2, либо тех и других:Слайд 151.2. Вычитание
Разность двух совместимых отношений R1 и R2
с одинаковыми заголовками есть отношение R, состоящее из множества кортежей
отношения R1, не принадлежащих отношению R2.Обозначение: R1 MINUS R2.
В предыдущем примере
R1 MINUS R2=∅.
Слайд 161.3. Пересечение
Пересечением двух совместимых отношений R1 и R2
с одинаковыми за-головками называется отношение R, включающее в себя кортежи,
принад-лежащие одновременно отношениям R1 и R2.Обозначение: R=R1 INTERSECT R2.
В примере 1 R1 INTERSECT R2 = R1.
Слайд 171.4. Декартово произведение
Декартовым произведением отношения R1 с длиной
кортежей k1 и отношения R2 с длиной кортежей k2, которые
не имеют одинаковых имен атрибутов, есть отношение R с длиной кортежей k1+k2, заголовок которого представляет собой сцепление заголовков отношений R1 и R2, и состоящее из таких кортежей, что первые k1 элементов принадлежат отношению R1, а последние k2 кортежей принадлежат отношению R2.Обозначение: R=R1 TIMES R2.
Слайд 18Замечание 1
В реляционной алгебре используется расширенный вариант декартова
произведения двух отношений, при котором элементы кортежей двух исходных отношений
сливаются, что означает удаление лишних скобок, то есть вместо упорядоченной пары((a, b), (c, d)) пишут (a, b, c, d). Здесь
(a, b)∈R1, (c, d)∈R2.
Слайд 19Пример 2
Пусть отношение R1 представляет собой множество номеров
всех текущих поставщиков {S1, S2, S3, S4, S5}, а отношение
R2 – множество номеров всех деталей {P1, P2, P3, P4, P5, P6}. Результатом операции R=R1 TIMES R2 является множество всех пар типа «поставщик-деталь», то естьR={(S1, P1), (S1, P2),…, (S5, P6)}.
Таким образом, отношение R будет состоять из 30 кортежей по 9 полей в каждом.
Слайд 20Замечание 2
Напрямую операция декартова произ-ведения на практике не
используется, однако, она является составной частью операции соединения. Поэтому данная
операция важна в концептуальном плане. Кроме того, операция декартова произведения используется в языке запросов SQL.Слайд 211.5. Выборка (ограничение)
Выборка отношения R по формуле f
представляет собой новое отношение с таким же заголовком и телом,
состоящим из тех и только тех кортежей, которые удовлетворяют истинности логического выражения, задаваемого формулой f.При этом для записи формулы f используются имена атрибутов, константы, логические операции and, or, not, операции сравнения и скобки.
Обозначение: R WHERE f
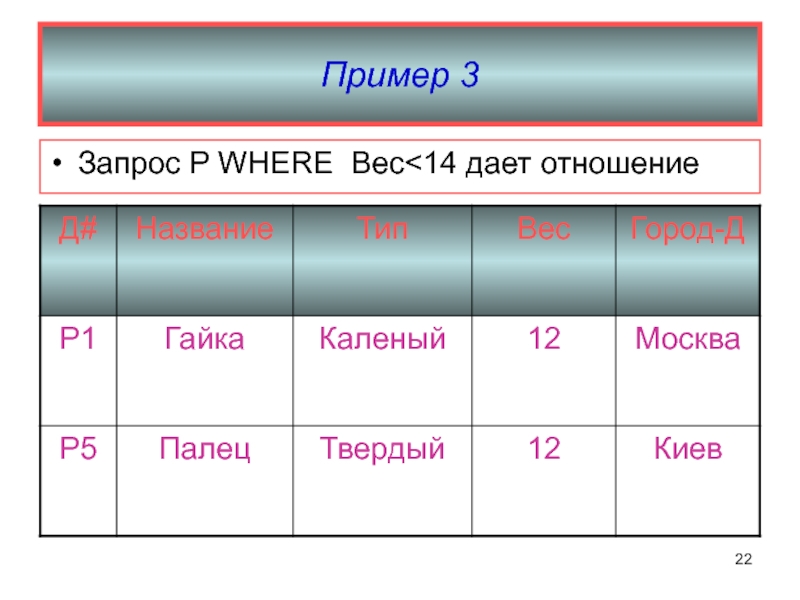
Слайд 23Пример 4
Для операции выборки используют также обозначение
SELECT (имя таблицы: условие выбора)
Например, по
запросу SELECT (SP: П# =‘S1’ and Д#=‘P1’) получим следующее отношение:
Слайд 24 Проекция отношения A на различные атрибуты X, Y,
…, Z, где множество {X, Y, …, Z} является
подмножеством полного списка атрибутов заголовка отношения A, представляет собой отношение с заголовком X, Y, …, Z и телом, содержащим кортежи отноше-ния A, за исключением повторяющихся кортежей.Обозначение: [X, Y, …, Z].
1.6. Проекция (PROJECT)
Слайд 25Дополнительные варианты записи операции проекции
Отсутствие списка атрибутов подра-зумевает указание всех
атрибутов (операция тождественной проекции).
Выражение вида A[ ] означает пустую проекцию,
результатом которой являет-ся пустое отношение.Операция проекции может применяться и к результату выборки.
Слайд 26Замечание 3
Если операцию выборки можно представить как исключение
ненужных кортежей, то опера-цию создания проекций можно представить как исключение
ненужных атрибутов.Слайд 271.7. Деление
Операция деления определена для двух отношений R1
и R2 при следующих условиях: отношение R1 должно иметь минимум
два простых или составных атрибута A и B, а отношение R2 должно содержать атрибут B, при этом атрибуты A и B должны быть определены на одном и том же домене.Слайд 28Результатом деления отношения R1на отношение R2 является отношение R с
заголовком A и телом, состоящим из кортежей r таких, что
в отношении R1 имеются кортежи (r, s), причем множество значений s включает множество значений атрибута B в отношении R2.Обозначение: R = R1 DIVIDEBY R2.
На практике операция деления нужна для того, чтобы мы могли выполнять квантор-ные операции ∀x и ∃x.
Слайд 29Пример 5
Пусть R1 - проекция SP[П#, Д#], а
R2 – отношение с заго- ловком Д# и телом {P2,
P4}.Слайд 30Результатом деления отношения R1 на отношение R2 будет отношение с
заголовком П# и телом {S1, S4}.
Операция деления является обратной
к операции декартова произведения: если отношение является декартовым произведением двух отношений R1 и R2, то мы можем получить таблицу R1, разделив декартово произведение на R2, то есть(R1 TIMES R2) DIVIDEBY R2 = R1.
Иногда используют и такое обозначение: (R1*R2)/R2=R1, где декартово произведение обозначено символом *, а деление – символом / .
Слайд 311.8. Соединение
Операция соединения используется для связывания данных между
отноше-ниями. Это, возможно, наиболее важ-ная функция любого языка БД.
В общем случае соединением отношения R1 по атрибуту A с отношением R2 по атрибуту B (отношения R1 и R2 не имеют общих атрибутов) является результат выполнения операции (R1 TIMES R2) WHERE A ∙ B, где ∙ - логическое выражение над атрибутами A и B, определенными на одном и том же домене.Слайд 32У операции соединения есть несколько вариантов:
естественное соединение (обо-значение: JOIN
(R1, R2));
тета-соединение;
эквисоединение (обозначение: EQUIJOIN (R1, R2)) - частный
слу-чай тета-соединения;внешнее соединение (обозна-чение: OUTERJOIN (R1, R2)).
Слайд 331.8. 1. Естественное соединение
Естественное соединение (NATURAL JOIN) –
это операция, связывающая отношения, когда общие атрибуты имеют равные значения.
Общее определение естественного соедине-ния таково: пусть отношения R1 и R2 имеют общие атрибуты C1, C2, … , Cn. Тогда операция JOIN(R1, R2) выпол-няется за следующие три шага:Слайд 34 Берется декартово произведение отношений R1 и R2. В результате
получается отношение R, содержащее по два столбца на каждый атрибут
C1, C2, … , Cn.
2) Из отношения R исключаются все кортежи кроме тех, в которых значения атрибутов C1, C2, … , Cn из отношения R1 равны соответственно значениям этих кортежей в отношении R2.
3) Операцией проектирования исключа-
ется одна копия кортежей C1, C2, … , Cn.
Слайд 351.8. 2. Тета-соединение и эквисоединение
Тета-соединение – операция, связыва-ющая
отношения, когда значения из определенных атрибутов находятся в определенном соотношении.
Общий вид тета-соединения следующий:JOIN (R1, R2: X ∙ Y), где R1, R2 - соединяемые отношения, а ∙ - одно из бинарных отношений: =, ≠, <, >, < =, > =, X и Y – атрибуты отношений R1 и R2.
Тета-соединение, основанное на отношении равенства определенных атрибутов, называется эквисоединением.
Слайд 36
Замечание 4
Тета-соединение, в отличие от естественного соединения, не
включает удаления одного или более атрибутов на последнем шаге 3).
Так, если отношение R1 содержит k атрибутов, а отношение R2 – m атрибутов, то тета-соединение будет состоять из k+m атрибутов.Слайд 371.8. 3. Внешнее соединение
Внешнее соединение является расширением естественного
соединения, включает все кортежи из обоих отношений и гарантирует, что
каждый кортеж из обоих исходных отношений будет представлен в отношении соединения хотя бы один раз. Внешнее соединение выполняется в два этапа. Сначала выполняется естественное соединение, затем, если какой-либо кортеж одного из исходных отношений не подходит ни к какому кортежу второго отношения, он включается в отношение соединения, а все дополнительные кортежи заполняются пустыми значениями (NULL).Слайд 38Пример 6 (эквисоединение)
Найдем соединение отношений S и P
по общему атрибуту, характеризующе-му город (в отношении S – это
город_П, а в отношении P – город_Д). Поскольку условие операции требует одинаковости имен атрибутов, по которым выполняется соединение, то применяется операция переименования атрибутов - RENAME:(S RENAME Город_П as Город) JOIN
(P RENAME Город_Д as Город).
Слайд 40
Обзор дополнительных операций реляционной алгебры, предложенных Дейтом
2Д. Операция расширения, заключающаяся
в добавлении нового атрибута в данное отношение, значения которого получаются
путем некоторых скалярных вычислений:EXTEND <имя отношения> ADD <выражение> AS <имя нового атрибута>
1Д. Операция переименования атрибутов:
RENAME <имя отношения> <старое имя атрибута> AS <новое имя атрибута>
(см. пример 6)
Слайд 41В операции расширения имя нового атрибута не должно повторять имен
имеющихся в данном отношении атрибутов и его значения вычисляются по
правилам, заданным в <выражении>; имя нового атрибута не должно входить в <выражение>.Помимо обычных алгебраических операций и операций сравнения в <выражении> можно использовать различные функции, называе-мые итоговыми, такими как COUNT (количество), SUM (сумма), AVG (среднее), MAX (максимальное), MIN (минимальное), например:
EXTEND (P JOIN SP) ADD (Вес * количество) AS общий_вес.
Слайд 423Д. Операция подведения итогов
Синтаксис этой операции имеет вид:
SUMMARIZE BY () ADD
AS <имя нового атрибута>,где <имя исходного отношения> может задаваться заключенным в круглые скобки выражением реляционной алгебры; <список атрибутов> представляет собой разделен-ные запятыми имена атрибутов исходного отношения; <выражение> - скалярное выражение реляционной алгебры.
Слайд 43Результатом операции подведения итогов является отношение R с заголовком, состоящим
из атрибутов списка, расширенного новым атри-бутом. Для получения отношения R
сначала выполняется операция проекции исходного отношения на атрибуты A1, A2,…, An, после чего каждый кортеж проекции расши-ряется новым (n+1)-ым атрибутом.Слайд 44Пример 6
Пусть требуется вы-числить число пос-тавок по каждому
из поставщиков. Это можно осуществить с помощью операции подведения итогов:
SUMMARIZE SP BY (П#) ADD COUNT AS Кол-ство_поставокПолучим отношение
В приведенной опера- рации функция COUNT определяет количество кортежей в каждой из групп исходного отно-шения.
Слайд 454Д. Операция присваивания
Синтаксис операции:
:= ,
где оба выражения
задают совмести-мые по структуре отношения. Типичный случай выражений: в левой
части – имя отношения, а в правой – некоторое выражение реляционной алгебры.Слайд 465Д. Операция вставки
Синтаксис операции:
INSERT INTO ,
где оба выражения должны быть совместимы по структуре. Результатом
этой операции является вставка полученных кортежей в отношение, заданное в <выражение-цель>, например:INSERT (S WHERE Город_П = ‘Москва’) INTO Temp
Слайд 476Д. Операция обновления
Синтаксис операции:
UPDATE ,
где
представляет собой последовательность разделен-ных запятыми операций присваивания вида
<атрибут>:= <скалярное выраже-ние>, например:UPDATE WHERE Тип:=‘Каленый’,
Город:= ‘Киев’
Слайд 487Д. Операция удаления
8Д. Операции реляционного сравнения
Синтаксис операции 7Д:
DELETE ,
где представляет собой ре-ляционное выражение, описывающее удаляе-мые кортежи.
К операциям 8Д относятся: =, ≠ (или < >), <, ≤ (или < =), >, ≥ (или > =).Слайд 49Замечание 5
При записи выражений в реляционной алгебре следует
придерживаться следующих правил:
- должен быть определен приоритет выполнения
операций. Для изменения порядка выполнения операций в выражениях, как обычно, используются круглые скобки;Слайд 50 выражения можно заменять другими выражениями, получающи- мися с помощью
тождественных преобразований;
составляя выражение, нужно обеспечивать совместимость участ-вующих в
операциях отношений. При необходимости изменения заголовков отношений следует выполнять переименование атри-бутов.Слайд 51 2. Реляционное исчисление
Принципиальное отличие между реляционной
алгеброй и реляционным исчислением состоит в том, что в первом
случае процесс получения искомого результата описывается явным образом путем указания набора операций, которые надо выполнить, а во втором – указываются свойства искомого отношения без конкретизации процедуры его получения.Слайд 52Понятие реляционного исчисления, как языка работы с БД, было впервые
предложено Э. Коддом. Им же был разработан язык ALPHA –
прототип программно реализованного языка QUEL, который некоторое время конкурировал с языком SQL.Существует два варианта реляционного исчисления: исчисление кортежей и исчисление доменов.
Слайд 532.1. Исчисление кортежей
В исчислении кортежей, как и в
про-цедурных языках программирования, сначала нужно описать используемые переменные, а затем
записывать неко-торые выражения. Описательную часть исчисления можно представить в виде:RANGE OF <переменная> IS <список>,
где RANGE, OF, IS – ключевые слова,
Слайд 54
- идентификатор пере- менной кортежа (области значений), а
- последовательность одного или более элементов, разделенных запятыми, то есть
конструкция вида.
Вся конструкция RANGE указывает идентификатор переменной и область ее допустимых значений. Список эле-ментов содержит элементы, каждый из которых является либо отношением, либо выражением над отношением.
Слайд 55Все элементы списка должны быть сов-местимы по типу, то есть
соответ-ствующие элементам отношения должны иметь идентичные заголовки. Область допустимых значений
<переменной> об-разуется путем объединения значений всех элементов списка. Так, запись RANGE OF T IS X1, X2 означает, что область определения переменной T включает в себя все значения из отно-шения, которое является объединением отношений X1 и X2.Слайд 56Пример 1
Варианты описаний:
RANGE OF SX IS S;
RANGE OF
SPX IS SP;
RANGE OF SY IS (SX) WHERE SX.Город_П =
‘Москва’, (SX) WHERE EXISTS SPX (SPX. П# = X. П# AND SPX. Д# = ‘P1’).Слайд 57Переменные SX и SPX в первых двух описаниях определены соответственно
на отношениях S и SP. В третьем опи-сании переменная SY
может принимать значения из множества кортежей отно-шения S для поставщиков из г. Москвы или поставщиков деталей P1. Служеб-ное слово EXISTS означает сущест-вование хотя бы одного кортежа, удов-летворяющего условию, записанному в последних круглых скобках.Слайд 58Пример 2
Записать выражение на языке исчи-сления кортежей, соответствующее
за-просу «Получить имена поставщиков, которые поставляют все детали».
SX.
Город_П WHERE FORALL PX (EXISTS SPX (SPX.П# = SX.П# AND SPX. Д# = SX. Д#)) или (второй вариант этого же запроса):SX. Город_П WHERE NOT EXISTS PX (NOT EXISTS SPX (SPX. П# = SX.П# AND SPX. Д# = SX. Д#))
Слайд 59Замечание
В исчисление кортежей можно добавить вычислительные функ-ции из
реляционной алгебры: COUNT, SUM, AVG, MAX, MIN. Тогда это исчисление
будет обладать вычислительной полно- той.Слайд 602.2. Исчисление доменов
Исчисление доменов было предложено Лакроиксом и
Пиротте, которые на его основе разработали язык ILL. Другими языками,
основанными на исчислении доменов, являются языки FQL, DEDUCE, а также QBE.В исчислении доменов основой любого запроса выступают переменные доме-нов. Переменная домена – это скалярная переменная, значения которой охватывают элементы некоторого домена.
Слайд 61Отличительной особенностью исчи-сления доменов от исчисления кортежей является то, что
в нем поддерживается дополнительная форма условия, называемого условием принадлежности. В
общем виде это условие записывается так:R(A1:η1, A2:η2, …),
где Ai – атрибут отношения R, а ηi – переменная домена или литерал.
Слайд 62Проверяемое условие будет истинным тогда и только тогда, когда существует
кортеж в отношении R, имеющий атрибуты Ai, равные заданным в
выражении соответ-ствующим значениям ηi.Слайд 63Примеры выражений исчисления доменов
(SX) WHERE S (П#:SX) – множество всех
номеров поставщиков отношения S;
(SX) WHERE S (П#:SX, Город_П: ‘Москва’ –
множество поставщиков из Москвы;NAMEX WHERE EXISTS SX (S(П#:SX, Имя: NAMEX) AND FORALL PX (IF P (Д#:PX) THEN SP (П#:SX, Д#:PX))).



















![Теоретические языки запросов в реляционных БД Дополнительные варианты записи операции проекцииОтсутствие списка атрибутов подра-зумевает указание всех атрибутов Дополнительные варианты записи операции проекцииОтсутствие списка атрибутов подра-зумевает указание всех атрибутов (операция тождественной проекции).Выражение вида A[ ]](/img/tmb/2/154387/d857e412ca7781bf049ac34b8270a477-800x.jpg)



![Теоретические языки запросов в реляционных БД Пример 5 Пусть R1 - проекция SP[П#, Д#], а R2 – Пример 5 Пусть R1 - проекция SP[П#, Д#], а R2 – отношение с заго- ловком Д#](/img/thumbs/73160063249fc9796cc989bacc84aab9-800x.jpg)