ТЕОРИЯ АБСТРАКТНЫХ АВТОМАТОВ

из чего сделан автомат.
Важно лишь то, что он воспринимает

некоторые сигналы как команды и по каждой команде выполняет некоторое действие, переходя из одного состояния в другое.
Поэтому можно считать, что каждый автомат описывается:
- набором возможных состояний,
- списком допустимых команд,
- перечислением того, из какого состояния в какое переходит автомат под воздействием каждой команды.

можно обозначить буквами, скажем, a и b, или цифрами, состояния

автомата — буквами q1, q2, ..., qm,
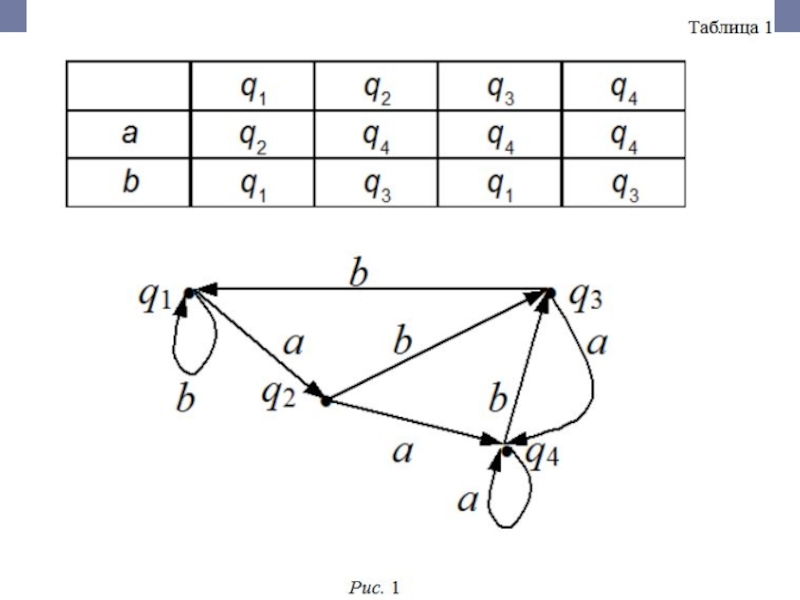
а перечислить варианты перехода из одного состояния в другое можно с помощью таблицы (см. табл. 1).
В клетке, стоящей на пересечении строки и столбца, указывается то состояние, в которое переходит автомат, находившийся в состоянии, которое указано в заголовке того же столбца, и получивший команду, указанную в заголовке той же строки.

— орграфом.
Вершинами орграфа являются состояния автомата, дугами — переходы

из одного состояния в другое.
На каждой дуге имеется метка, показывающая, по какой команде осуществляется такой переход.
Тогда автомат, описанный табл. 1, изобразится так, как показано на рис. 1.
Обратите внимание, что из каждой вершины выходит столько стрелок, сколько символов в алфавите, при этом каждый символ употреблен ровно один раз.

в нем находится автомат до начала работы.
Договоримся начальное состояние

всегда обозначать q1.
Некоторые из состояний являются заключительными — приведение автомата в это состояние является целью управления автоматом с помощью той или иной последовательности команд.
Конечных состояний может быть несколько.
Обозначать тот факт, что данное состояние конечное, будем буквой К в скобках около обозначения данного состояния.
Например, q2(К).

ему такой последовательности команд, которая переводит его из начального состояния

в какое-либо конечное.
Поскольку каждая команда обозначена буквой, то набор команд, понимаемых данным автоматом, можно считать некоторым алфавитом А.
Тогда последовательность команд, т.е. программа, будет записываться как слово в этом алфавите.
Например, слово abа переводит автомат, описанный табл. 1, из начального состояния q1 в состояние q4.
Можно сказать, что слово abа задает на орграфе данного автомата некоторый маршрут из состояния q1 в состояние q4.

из начального состояния в одно из конечных состояний, образует некий

формальный язык.
Этот язык называется языком, распознаваемым данным автоматом.
Если для некоторого языка существует хотя бы один автомат, который этот язык распознает, то такой язык называют распознаваемым.

не будет обязан однозначно реагировать на каждую команду, а может

по той или иной команде переходить в какое-нибудь из состояний, или вообще не менять состояние.
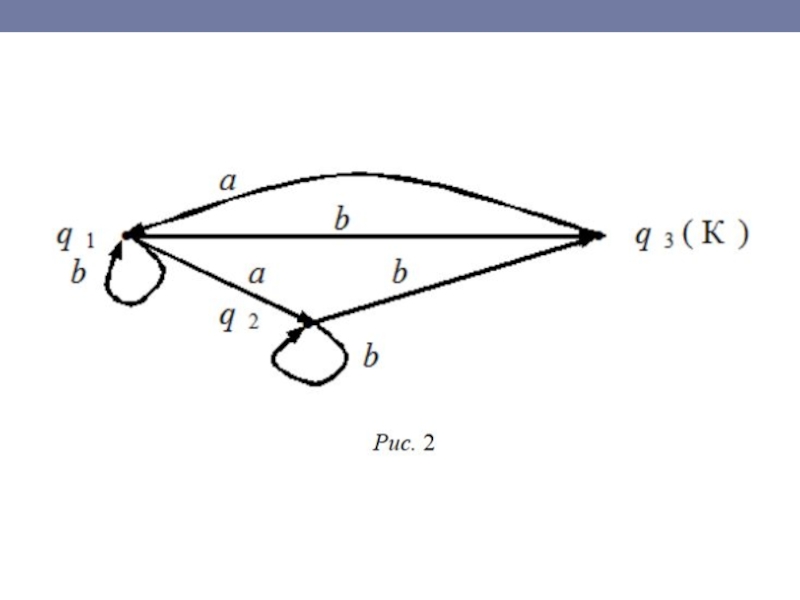
Конечно, мы по-прежнему можем изображать такой автомат размеченным орграфом, только теперь стрелок с одним и тем же символом алфавита, выходящих из одной вершины, может быть несколько или ни одной (см. рис. 2).
Такой автомат называют недетерминированным.

по-прежнему будем обозначать его q1.
Одно или несколько состояний являются

конечными.
Цель та же — перевести последовательностью команд автомат из начального состояния в какое-нибудь конечное.
Как и ранее, языком, распознаваемым данным недетерминированным автоматом, называется множество слов, для каждого из которых существует хотя бы один путь, переводящий автомат из начального состояния в какое-либо конечное состояние.
Отличие, однако, в том, что теперь слово (т.е. последовательность команд) вовсе не каждый раз переведет автомат из начального состояния в то же самое конечное.

состояние.
Например, слово bаb может перевести автомат, изображенный на рис.

2, из состояния q1 как в состояние q1, так и в состояние q3.
Можно сказать, что недетерминированный автомат до определенной степени моделирует поведение человека — одни и те же слова могут приводить к разным реакциям, а иногда и просто к «зависанию».

недетерминированного автомата.
Поэтому множество распознаваемых языков содержится в множестве всех

языков, распознаваемых недетерминированными автоматами.
Удивительно, что верно и обратное утверждение: всякий язык, распознаваемый каким-либо недетерминированным автоматом, является распознаваемым.

называть эквивалентными, если распознаваемые ими языки совпадают.
Естественно для заданного

распознаваемого языка интересоваться минимальным автоматом среди всех автоматов, распознающих данный язык.
Надо сказать, математики весьма преуспели в исследовании этого вопроса.

можно называть эквивалентными, если распознаваемые ими языки совпадают.
Естественно для

заданного распознаваемого языка интересоваться минимальным автоматом среди всех автоматов, распознающих данный язык.
Надо сказать, математики весьма преуспели в исследовании этого вопроса.

не более одного перехода из каждого состояния.
Если для представления

функции переходов используется таблица, то каждая запись в ней представляет собой единственное состояние.
Состояния q автомата М и q' автомата М' считаются эквивалентными, если оба автомата, получив одну и ту же (любую) входную последовательность символов, перерабатывают ее в одинаковую выходную последовательность.
Автоматы М и М' называются эквивалентными, если для каждого состояния автомата М существует эквивалентное ему состояние автомата М' и наоборот.

могут иметь различное число внутренних состояний.
Понятие эквивалентности состояний применимо и

к одному автомату (формально можно считать, что М и М' совпадают).
Для одного автомата эквивалентными будут различные состояния, через которые одна и та же входная последовательность символов преобразуется в одинаковую выходную.

виде композиции нескольких автоматов.
Возникающие здесь проблемы являются типичными для

структурной теории автоматов и вместе с тем они аналогичны проблемам, возникающим в современной алгебре.
Такие проблемы возникают, когда рассматривается представление данной алгебраической системы в виде нескольких более простых систем того же вида.

можно ставить по-разному.
Можно рассматривать представление автоматов в виде:

- прямой суммы,
- произведения,
- параллельно-последовательного соединения и т. п.
Представляет интерес прежде всего тот случай, когда автоматы, составляющие композицию, являются в некотором смысле более простыми, чем исходный автомат.

меньшее число состояний,
- меньше входных каналов,

- если их функция переходов в некотором смысле более простая, и т. п.
Следовательно, задача А допускает много вариаций.

аналогии из алгебры, можно определить, что автомат А моделирует автомат

В в том и только том случае, когда В изоморфен некоторому подавто­мату автомата А.
Это называется моделированием 1-го рода.
Однако такое заимствованное из алгебры по­нятие, где главный интерес представляют эле­менты алгебры и отношения между ними, яв­ляется слишком сильным и не отражает спе­цифики теории автоматов.

автомата.
Эквивалентными счи­таются два автомата, имеющие одинаковое по­ведение (но, возможно,

различное число со­стояний).
Тогда естественно определить, что автомат А моделирует автомат В, если его поведение, с точностью до переименования входных и выходных букв, совпадает с пове­дением автомата В.
Или точнее, автомат А моделирует автомат В в том и только том слу­чае, когда В является гомоморфным образом некоторого подавтомата автомата А.
Это называется модели­рование 2-го рода.

базисом конечных автоматов), если из них можно построить любой наперед

заданный структурный автомат.
В 1964 г. М.И. Кратко доказал несуществование алгоритма для определения полноты системы.
Под полнотой понимают выразимость всех функций через заданные.
Под выразимостью понимается возможность получения функций одного множества через функции другого с помощью заданных операций.

к задаче о полноте автоматного базиса.
Первый подход связан с расширением

понятия равенства автоматов и их множеств.
Возникли дополнительные понятия полноты автоматного базиса.
Второй подход связан с вариацией операций, применяемых к автоматам.
Третий подход связан с изучением полноты в подклассах автоматов.
Четвертый подход связан с ограничением на исследуемые системы автоматов.

алгоритмически неразрешимой.
Эта проблема является темой для многих научных диссертаций, поэтому

далее углубляться в решение этих задач мы не будем.

из шести элементов. Назовите их.
Назовите две основные модели, описывающие функционирование

абстрактных автоматов. Опишите законы их функционирования.
Назовите два способа задания автоматов. По представленной таблице составьте граф. Какая модель автомата представлена в таблицах.

эквивалентными?
Что называют декомпозицией автоматов?
Что называют базисом конечных автоматов?