Теория перемещений. Основные понятия и теоремы Под перемещением какой-либо

понимается изменение ее координат в результате деформации элементов сооружения.
Основные гипотезы,

используемые при определении перемещений:
- рассматриваются линейно деформируемые системы, подчиняющиеся закону Гука:

- используется принцип суперпозиции (наложения), согласно которому результат действия системы сил равен сумме результатов действия отдельных сил:

- используются понятия обобщенной силы и обобщенного перемещения:
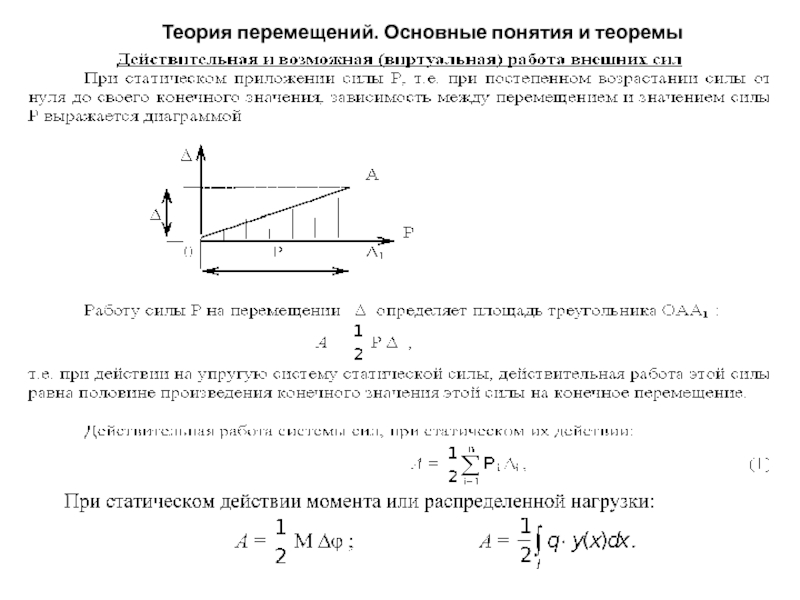
а) под обобщенной силой понимается любая сила или группа сил (например: пара сил, равномерно распределенная нагрузка и т.п.).
б) обобщенное перемещение - это перемещение, соответствующее обобщенной силе, которое при умножении на обобщенную силу дает работу, т.е. это множитель при обобщенной силе в выражении работы:

изгибающего момента М

образом, результат перемножения двух эпюр равен произведению площади одной из

них на ординату y0 другой (прямолинейной) эпюры, взятую под центром тяжести площади первой эпюры.

определения перемещений с использованием правила Верещагина:
1) строится грузовая эпюра Мр,

от действия заданных внешних нагрузок;
2) по направлению искомого перемещения прикладывается единичная сила Р=1 или единичный момент М=1 и строится единичная эпюра;
3) перемножая эпюры по правилу Верещагина, определяют искомое перемещение. Эпюры перемножают по участкам, результат перемножения берут со знаком "+ ", если эпюры расположены по одну сторону элемента и со знаком минус "- ", если по разные.