Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорія прийняття рішень
Содержание
- 1. Теорія прийняття рішень
- 2. Теорія прийняття рішень3 МодуляЛекцій-15
- 3. Теорія прийняття рішень3 МодуляЛПЗ-15 Викладач– ас.
- 4. Лекція 1. ВСТУП В ПРИЙНЯТТЯ РІШЕНЬ.МОДЕЛЬ ПРОБЛЕМНОЇ
- 5. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006/20 1. Проблема прийняття Рішень
- 6. Пусть никто не думает, будто можно всегда
- 7. Необхідність Прийняття рішеньКожна людина протягом свого
- 8. ОПРОПР – особа, що приймає рішенняОсновна функція
- 9. Ітераційна процедура прийняття Рішення Комп”ютерне моделювання процесів
- 10. Етапи прийняття рішень.аналіз проблеми та середовища (цілі
- 11. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006/20 2. Науки про прийняття Рішень
- 12. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 13. Теоретико-системные основы математического моделирования (с) Н.М. Светлов,
- 14. цільова функція (критерій керованості): Ф=F(x1,x2,:,xn) →
- 15. Дом завданняНаведіть моделі для задачОптимізації виробничої програмиОптимізації раціонівОптимізації внесення добрив…….іншіМатематична модель задачі оптимізації (досл. операцій)
- 16. Теорія прийняття рішень (ТПР) - це математична
- 17. Процес прийняття рішення включає: 1) Визначення
- 18. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006/20 3. Постановка Задачі прийняття Рішенння
- 19. Модель проблемної ситуації (формулювання задачі прийняття рішення
- 20. Критерії ( до п.4 – опис системи
- 21. Модель проблемної ситуації (формулювання задачі прийняття рішення
- 22. Модель проблемної ситуації (формулювання задачі прийняття рішення
- 23. Приклад 1 Купівля фотоапарата ОПР
- 24. Приклад 1 Купівля фотоапарата . Невизначеним
- 25. Приклад 1 Купівля фотоапарата ОПР
- 26. Приклад 1 Купівля фотоапарата Відмінність
- 27. Приклад 1 Купівля фотоапарата Відмінність Теорії
- 28. Приклад 2. Зарахування студента в СуМДУ.Кількість балів,
- 29. Приклад 3 Вивчення дисципліни Х. .Стратегії
- 30. Приклад 3 Вивчення дисципліни Х. .
- 31. Cистема переваг, задана безпосередньо на S..У простіших
- 32. Задачі вибору.Задачі, в яких система переваг P
- 33. Принцип оптимальності.Правила, що дозволяють знаходити S *
- 34. 2. Класифікація Задач Прийняття Рішень Теорія Прийняття рішень © ЄА. Лавров, 2014-2019/14
- 35. Класифікація Задач Прийняття Рішень . В
- 36. Класифікація Задач Прийняття Рішень .2) В
- 37. Класифікація Задач Прийняття Рішень 3)
- 38. Класифікація Задач Прийняття Рішень .4) Залежно
- 39. 5.Прийняття рішень в АСУ. Поняття СППР/100
- 40. 5.Прийняття рішень в АСУ. Поняття СППР/100 Моделі
- 41. 5. Поняття СППР/100An executive information system (EIS)-Executive
- 42. Додатковий матеріал
- 43. Принципы классификации задач принятия решений степень определённости
- 44. Задача принятия решений
- 45. Определенность исходных данных в задачах принятия решенийЗадачи
- 46. Методы оптимизации в СППРметоды линейного и динамического
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Теорія прийняття рішень
3 Модуля
Лекцій-15
Лектор – д.т.н. проф. Лавров Евгеній Анотолійович
http://www.famous-scientists.ru/13333/
Prof_lavrov@mail.ru
Теорія
Прийняття рішень
Слайд 3Теорія прийняття рішень
3 Модуля
ЛПЗ-15
Викладач– ас. Криводуб Анна Сергіївна
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 4Лекція 1. ВСТУП В ПРИЙНЯТТЯ РІШЕНЬ.МОДЕЛЬ ПРОБЛЕМНОЇ СИТУАЦІЇ
Зміст лекції:
Проблема прийняття
Рішень
Науки про прийняття рішень
Постановка Задачі прийняття Рішенння
Класифікація Задач
Прийняття РішеньПрийняття рішень в АСУ. Поняття СППР
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/100
Слайд 5Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
1. Проблема прийняття
Рішень
Слайд 6
Пусть никто не думает, будто можно всегда принимать безошибочные решения,
напротив, всякие решения сомнительны; ибо в порядке вещей, что, стараясь
избежать одной неприятности, попадаешь в другую. Мудрость заключается только в том, чтобы, взвесив все возможные неприятности, наименьшее зло почесть за благо.Ларичев О. И.
Теория и методы принятия решений, а также Хроника
событий в Волшебных Странах: Учебник. - М.: Логос, 2000. -
296 с:
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 7 Необхідність Прийняття рішень
Кожна людина протягом свого життя постійно стикається
з ситуаціями, які вимагають від нього прийняття рішення «як поступити».
В одних випадках людина приймає рішення не замислюючись - на підсвідомому рівні, - якщо ситуація достатньо проста чи часто повторювана. Тоді рішення приймається на основі інстинкту, інтуїції або особистого досвіду. В інших ситуаціях вирішення питання «як поступити?» Вимагає серйозних роздумів, іноді веде до необхідності порадитися з іншими людьми - більш досвідченими або тими, для яких, це рішення також важливо. У подібні ситуації можуть потрапляти і цілі колективи людей, коли від них вимагається прийняття спільного рішення. Ваші приклади………Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 8ОПР
ОПР – особа, що приймає рішення
Основна функція ЛПР - прийняття
рішень
Рішення ОПР визначає результат:
економ. ефект
прибуток
виграш
корисність
надійність Результат визначає корисність рішення і має бути оцінений кількісно
Вибір з безлічі
можливостей (орієнтований
на досягнення мети)
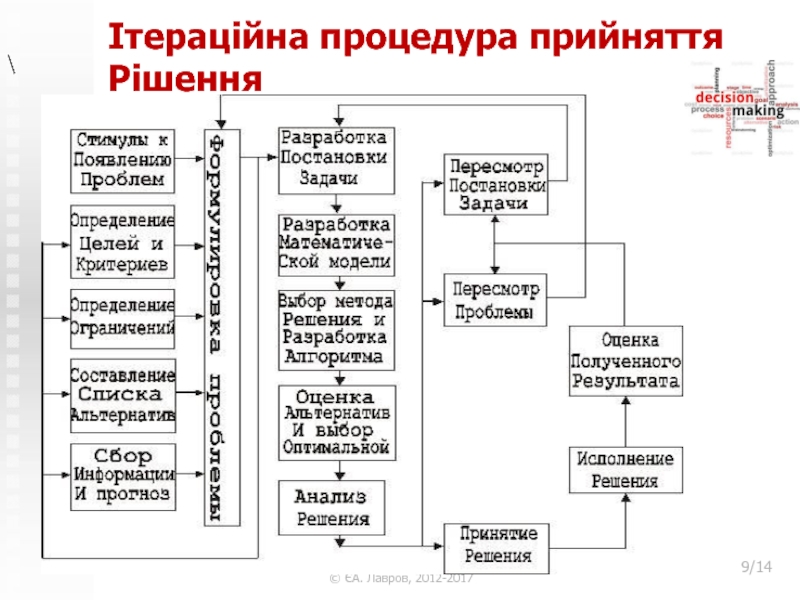
Слайд 9Ітераційна процедура прийняття Рішення
Комп”ютерне моделювання процесів і систем
©
ЄА. Лавров, 2012-2017
/14
Процесс принятия решений является сложной итерационной процедурой. Структурная
схема процесса принятия решений может иметь вид:
\Слайд 10Етапи прийняття рішень
.
аналіз проблеми та середовища (цілі прийняття рішення, їх
пріоритети, глибина і обмеження розгляду, елементи, зв'язку, ресурси середовища, критерії
оцінки);постановка задачі (визначення специфікацій задачі, альтернатив і критеріїв вибору рішення);
вибір (адаптація, розробка) методу розв'язання задачі;
вибір (адаптація, розробка) методу оцінки рішення;
вирішення завдання (математична і комп'ютерна обробка даних, імітаційні та експертні оцінки, уточнення і модифікація, якщо це необхідно);
аналіз та інтерпретація результатів.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 11Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
2. Науки про
прийняття Рішень
Слайд 12Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
fig1.gif
Рис. 1. Хронология
развития представлений об организационных системах
( за матеріалами ІПУ РАН)
http://www.mtas.ru/theory/obzor.phpХронологія розвитку уявлень про організаційні системи ,
управління і прийняття рішень
Слайд 13Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
С и с
т е м н и й
А н а л і зНауки про прийняття рішень
(межі умовні )
Дослідження
Операцій
______________
Задачі мат.
Програмування
( в умовах
визначеності)
Форм. постановки
Штучний
Інтелект
______________
Імітація
розумової
Діяльності
Експертні
системи
Теорія
Прийняття рішень
______________
Визначеність
Невизначеність
Ризик
Протидія
Слайд 14 цільова функція (критерій керованості): Ф=F(x1,x2,:,xn) → opt,
где xj (j=1,2,:,n) - параметри, що враховуються при ухваленні рішення
(характеризують ресурси прийняття рішень);умови, що відображають обмеженість ресурсів і дій ЛПР при ухваленні рішень :
gi(xj)
cj
Ваші приклади………змістовних постановок
Математична модель задачі оптимізації (досл. операцій)
Слайд 15Дом завдання
Наведіть моделі для задач
Оптимізації виробничої програми
Оптимізації раціонів
Оптимізації внесення добрив
…….
інші
Математична
модель задачі оптимізації (досл. операцій)
Слайд 16
Теорія прийняття рішень (ТПР) - це математична дисципліна,
покликана допомагати
людині виробляти «розумне» рішення у важких ситуаціях.
Будемо називати рішення
розумним, якщо людина врахувала при його прийнятті
всі істотні фактори, основні можливі наслідки, отримала оцінки кращих експертів, словом використав всю наявну на момент прийняття
рішення інформацію з точки зору своїх переваг, своєї інтуїції і досвіду.Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 17
Процес прийняття рішення включає:
1) Визначення цілей, з якими буде
здійснюватися майбутнє дію. Т.е. усвідомлення того, чого особа, що приймає
рішення (ОПР) хоче досягти. 2) Вибір найбільш переважного («найкращого», «оптимального» і т.п.) варіанта дій, що ведуть до досягнення поставлених цілей. 3) Реалізація обраного варіанту дій (рішення).ТПР може бути застосована для здійснення другого етапу цього процесу.
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 18Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
3. Постановка Задачі
прийняття Рішенння
Слайд 19Модель проблемної ситуації (формулювання задачі прийняття рішення (ЗПР).
Зазвичай в ЗПР
ній виділяють наступні елементи: 1) S - безліч варіантів дій,
що ведуть в тій чи іншій ступеня до досягнення поставленої мети, званих варіантами вирішення завдання, стратегіями або альтернативами. 2) G - безліч наслідків реалізації кожної із стратегій, званих ”исходами (рос)”. 3) Λ - безліч можливих значень невизначеного фактора - опис середовища ЗПР, тобто тих факторів, які впливають на отримання того чи іншого результату при реалізації тієї чи іншої стратегії При цьому кожен результат g представляється як функція від обраної стратегії s і значення невизначеного фактора λ: g=ψ(s,λ). 4) P - опис системи переваг ОПР на множині G.(див. далі)
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 20Критерії
( до п.4 – опис системи переваг)
Зазвичай для опису переваг
використовуються числові функції, звані критеріями, визначені на множині G.
Значення
критерію характеризує ступінь інтенсивності деякої властивості результату, важливого з точки зору поставленої мети.
В окремому випадку, коли перевагу вдається описати за допомогою одного
критерію K: G → E⊆R, перевага g’ 'краще g’’ ⇔ K(g’)>K(g’’). Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 21Модель проблемної ситуації (формулювання задачі прийняття рішення (ЗПР). - продовження
5)
θ - вся інша інформація про проблемну ситуацію, подана у
формалізованому вигляді. Наприклад, це може бути інформація про важливість критеріїв, про ставлення ОПР до ризику і т.п.Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 22Модель проблемної ситуації (формулювання задачі прийняття рішення (ЗПР). - продовження
6)
Необхідна дія на безлічі S, наприклад:
виділити кращий варіант,
підмножину
кращих варіантів,ранжувати варіанти,
класифікувати варіанти з S і т.п.
Як правило, розглядатимемо задачу виділення з S підмножини кращих варіантів.
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 23 Приклад 1 Купівля
фотоапарата
ОПР - покупець.
Кожна стратегія в
цьому завданні буде виглядати так:
«Купити фотоапарат моделі X».
Кожен
результат описується набором властивостей
купленого апарату, ступінь вираженості яких можна охарактеризувати чисельними критеріями:Вартість (сума в грн),
зручність користування (Оцінка за 10-бальною шкалою),
розмір одержуваних зображень (розмір матриці фотоапарата в мегапикселях),
зум об'єктива кратність),
компактність (сума вимірів по довжині, висоті і товщині)
і ін.
система переваг ОПР, відповідно, буде описуватися набором цих критеріїв.
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 24Приклад 1 Купівля
фотоапарата
.
Невизначеним чинником в цьому завданні можна
вважати, наприклад, заводський брак при випуску конкретного апарату.
Від ОПР
може бути отримана також інформація про важливість критеріїв (наприклад, «зручність важливіше ціни»)
обмеження на них («розмір матриці не менше, аніж 4 Mpix», «не дорожче 10 тис. грн. »).
В якості людини, покликаної допомогти здійснити вибір, може виступати продавець-консультант.
Його задача може зводитися до вказівки набору найбільш підходящих апаратів або до класифікації за ціною / якістю.
Характерною особливістю ЗПР є необхідність отримання від ЛПР
інформації про переваги P і
додаткової інформації θ про проблемну ситуацію.
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 25 Приклад 1 Купівля
фотоапарата
ОПР - покупець.
Кожна стратегія в
цьому завданні буде виглядати так:
«Купити фотоапарат моделі X».
Кожен
результат описується набором властивостей
купленого апарату, ступінь вираженості яких можна охарактеризувати чисельними критеріями:Вартість (сума в грн),
зручність користування (Оцінка за 10-бальною шкалою),
розмір одержуваних зображень (розмір матриці фотоапарата в мегапикселях),
зум об'єктива кратність),
компактність (сума вимірів по довжині, висоті і товщині)
і ін.
система переваг ОПР, відповідно, буде описуватися набором цих критеріїв.
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 26Приклад 1 Купівля
фотоапарата
Відмінність Теорії Прийняття Рішень від Дослідження операцій
(Мат.програмування)
Справа в тому, що в теорії прийняття рішень розглядаються складні
ситуації, для яких характерна принаймні одна з умов: наявність випадкових або невизначених факторів,
багатокритеріальність,
необхідність врахування думок декількох осіб з незбіжними інтересами.
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 27Приклад 1 Купівля
фотоапарата
Відмінність Теорії Прийняття Рішень від Дослідження
операцій (Мат.програмування)
Одне з найважливіших вихідних положень полягає в тому, що
в перерахованих випадках не існує оптимального в якомусь абсолютному сенсі вирішення, а можна говорити лише про «кращі» або «оптимальні» рішеннях з точки зору данної ОПР з його системою переваг. У цьому полягає відмінність ТПР від оптимізаційних постановок задач, прийнятих в теорії досл. операцій, математичного програмування, та інших областях математики.
В цих задачах підставою для вибору служить числовий критерій оптимальності (Цільова функція), що є мірою якості варіанту.
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 28Приклад 2. Зарахування студента в СуМДУ
.
Кількість балів, набрана абітурієнтами :
Іванов: математика - 128, література - 169.
Петров: математика -
133, література - 192. Стратегія S1 - прийняти Іванова,
стратегія S2 - прийняти Петрова.
З точки зору ITП - переважає стратегія S1,
з точки зору ф-ту Журналістики - стратегія S2.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 29Приклад 3
Вивчення дисципліни Х.
.
Стратегії поведінки при вивченні:
А
- не відвідувати групові заняття, не займатися самостійно. Б -
відвідувати, не займатися. В - не відвідувати, займатися. Г - відвідувати, займатися. Результати будуть оцінюватися за критеріями: К1 (оцінка на іспиті) зі шкалою: {5,4,3,2,1} (1 - не здав на перездачі), К2 (витрачені зусилля) зі шкалою: {багато, середньо, мало, ніяких}.Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 30Приклад 3
Вивчення дисципліни Х.
.
При таких шкалах теоретично можливо
20 різних результатів,
але
деякі з них, наприклад, що характеризуються
векторними оцінками(5, ніяких) або (1, багато),
на практиці майже не реалізуються.
В результаті вибору тієї чи іншої стратегії може настати той чи інший
результат з більшою чи меншою ймовірністю
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 31Cистема переваг, задана безпосередньо на S
.
.У простіших завданнях стратегії та
наслідки однозначно відповідають один одному (приклад 2).
В таких завданнях
можна вважати, що система переваг P ЛПР задана безпосередньо на безлічі S.Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 32Задачі вибору
.
Задачі, в яких система переваг P
ОПР задана безпосередньо
на безлічі порівнюваних варіантів S і потрібно виділити підмножину S
* кращих в деякому сенсі варіантів, називаються задачами вибору.Іноді вдається задачу прийняття рішення представити як послідовність задач вибору.
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 33Принцип оптимальності.
Правила, що дозволяють знаходити S * ⊆S називаються принципом
оптимальності.
Математично принцип оптимальності задається як відображення
χ: S*=χ(D),
де
D - мат.модель проблемної ситуації, що включає S, G, P, Λ, ψ, θ.
У теорії вибору вводиться до розгляду функція вибору C: S * = C (S).Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
Слайд 35Класифікація Задач
Прийняття Рішень
.
В основу класифікації можуть бути покладені
різні ознаки
Залежно від кількості рівноправних ЛПР розрізняють:
а) задачі
індивідуального прийняття рішення ( ОПР- один)б) задачі групового прийняття рішення або вибору (ОПР – декілька)
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 36Класифікація Задач
Прийняття Рішень
.
2) В залежності від середовища розрізняють ЗПР:
а) в умовах визначеності (невизначені фактори відсутні);
б) в умовах
ризику (маються випадкові чинники λ з відомими законом розподілу ймовірностіFλ (x) = P (λ
г) в умовах протидії (параметр λ характеризує активні дії супротивника).
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 37Класифікація Задач
Прийняття Рішень
3) Залежно від кількості критеріїв, які
використовуються для
оцінки результатів:
Однокритеріальні задачі
Багатокритеріальні задачі
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 38Класифікація Задач
Прийняття Рішень
.
4) Залежно від вимог, що пред'являються до
результату, розрізняють задачі:
а) вибору єдиного варіанта
б) вибору підмножини
варіантів
в) упорядкування варіантів
г) класифікації варіантів
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
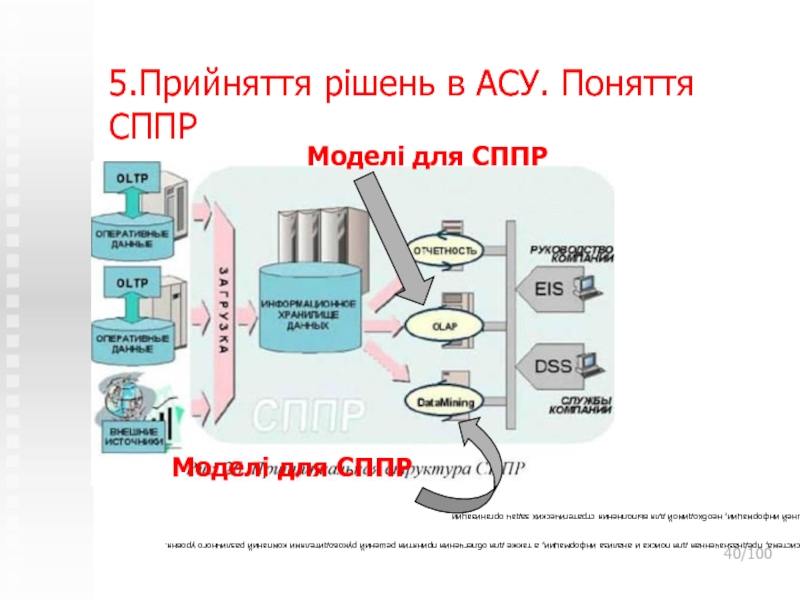
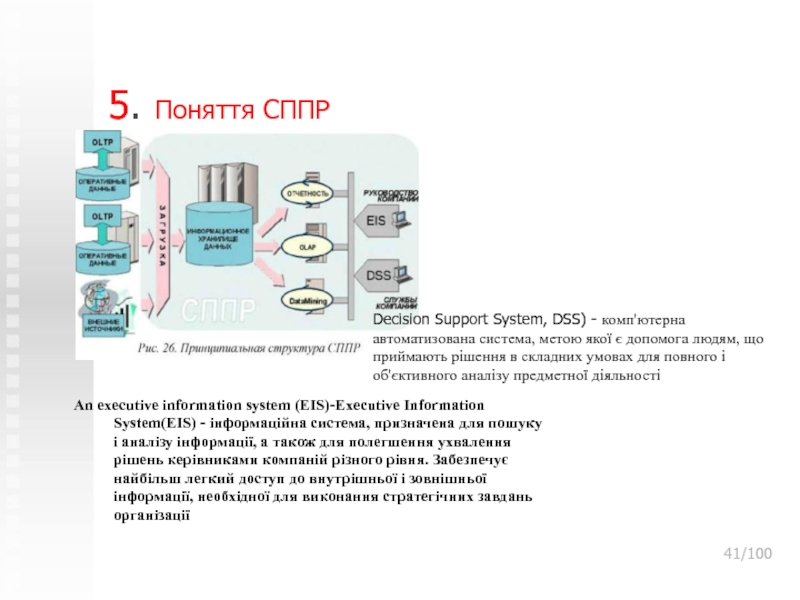
Слайд 405.Прийняття рішень в АСУ. Поняття СППР
/100
Моделі для СППР
Моделі
для СППР
Executive Information System (EIS) — информационная система, предназначенная для поиска
и анализа информации, а также для облегчения принятия решений руководителями компаний различного уровня. Обеспечивает наиболее легкий доступ к внутренней и внешней информации, необходимой для выполнения стратегических задач организации Слайд 415. Поняття СППР
/100
An executive information system (EIS)-Executive Information System(EIS) -
інформаційна система, призначена для пошуку і аналізу інформації, а також
для полегшення ухвалення рішень керівниками компаній різного рівня. Забезпечує найбільш легкий доступ до внутрішньої і зовнішньої інформації, необхідної для виконання стратегічних завдань організаціїExecutive Information System (EIS) —
Decision Support System, DSS) - комп'ютерна автоматизована система, метою якої є допомога людям, що приймають рішення в складних умовах для повного і об'єктивного аналізу предметної діяльності
Слайд 43Принципы классификации задач принятия решений
степень определённости информации
использование экперимента
для получения информации
количество ЛПР
возможность формальной постановки задачи
количество
этапов решенияколичество критериев
Слайд 44Задача принятия решений
Т-постановка
задачи ( напр. выбрать лучшую альтернативу или упорядочить набор альтернатив)
А-мн-во
доп. альтернативных вариантовK-мн-во критериев выбора (однокритер. и многокритер.задачи)
X-мн-во методов измерения предпочтений (напр. использование различных шкал)
F-отображение мн-ва доп. альтернатив в мн-во критериальных оценок (тип задачи-детерминир,вероятностный, или неопределенный)
G-система предпочтений эксперта (индивид. или коллективное принятие решений)
D-решающее правило, отражающее систему предпочтений
Слайд 45Определенность исходных данных в задачах принятия решений
Задачи принятия решений могут
быть поставлены и решены в условиях
детерминированных (определенности, формализованности, количественной
оцениваемости всех показателей)- методы мат. прогр.риска (возможные решения, исходы распределены вероятностно) –стат.данные, эксп. оценки
неопределенности (неопределенности, неточности, плохой формализуемости информации)- привлекаются знания экспертов
Слайд 46Методы оптимизации в СППР
методы линейного и динамического программирования (принятия решения
об оптимальном распределении ресурсов);
методы теории массового обслуживания (принятие решения в
системе со случайным характером поступления и обслуживания заявок на ресурсы);методы имитационного моделирования (принятие решения путем проигрывания различных ситуаций, анализа откликов системы на различные наборы задаваемых ресурсов);
методы теории игр (принятие решений с помощью определения стратегии в тех или иных состязательных задачах);
методы теории расписаний (принятие решений с помощью разработки календарных расписаний выполнения работ и использования ресурсов);
методы сетевого планирования и управления (принятие решений с помощью оценки и перераспределения ресурсов при выполнении проектов, изображаемых сетевыми графиками);
методы многокритериальной (векторной) оптимизации (принятие решений при условии существования многих критериев оптимальности решения)